EIP-8037 的雙資源計量氣體方程

01-14

本文為機器翻譯

展示原文

感謝在最近的會議中參與討論這些話題的各位與會者： Maria 、 Ansgar 、 Vitalik 、 Francesco 、 Caspar 、 Julian以及其他許多人。

1. 概述

EIP-8037統一併提高了狀態創建的 gas 費用。人們擔心gas 費用的增加可能會阻礙擴展性，因為用戶在狀態創建上花費的 gas 限額比例會更高，從而擠佔常規 gas 的使用。因此，研究人員一直在研究如何將狀態創建 gas 的限額從所有其他操作的目標和限制中分離出來，為狀態創建設置單獨的目標和限制。如果重新定價後，狀態創建 gas 的佔比從 30% 提高到 50%，那麼將狀態創建獨立出來將使所有其他操作的擴展性提升約 100%，這是一個非常誘人的方案。

針對此問題，已提出三種解決方案。除了常規的重新定價之外，以太坊還可以採用EIP-8011中提出的 gas 計量機制。gas 價格可以設置為隨 gas 上限動態變化，本文提出了一種可能的規範，EIP-8037 的最新版本也採用了類似的規範。另一種方案是採用計量狀態創建，以自適應 gas 成本來控制特定狀態的增長，如EIP-8075中所述。

本文分析了一個具體問題：當使用兩種不同的資源（常規 gas 和狀態創建 gas）時，每個區塊的基礎費用應該如何更新。本文的經驗教訓對 EIP-8011 和 EIP-8075 都適用，但對 EIP-8011 尤為重要，因為 EIP-8011 沒有目標機制來將兩種資源的消耗量控制在一定的相對水平。

首先，本文可視化了現有方法，例如應用max和average函數。然後，提出歐幾里得範數作為一種可行的折衷方案。此外，本文還探討了非對稱方法。計量氣體方程的非線性程度越高，其非對稱性就越強，從而可以最大限度地提高規模。最後，本文概述了最簡單的改進：多維氣體核算。在本文中，計量氣體G G 、常規氣體G 1 和狀態生成氣體G 2 均表示為常規氣體極限的分數。

2. EIP-8011 的最大功能

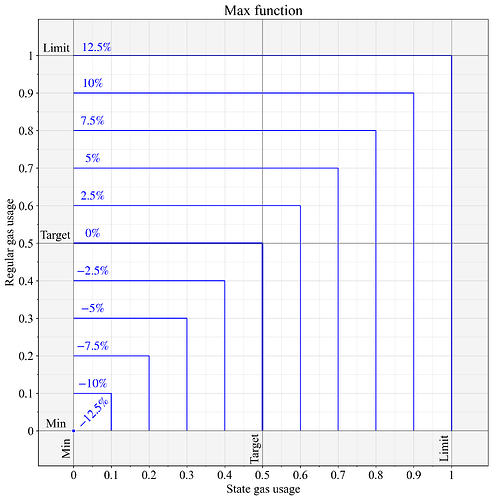
EIP-8011計算計量天然氣量G ，並將其輸入EIP-1559基本費用更新公式，計算方法為： G為所有獨立資源所用天然氣量的max 。圖 1 展示了計算結果。

一個值得關注的問題是擴展性提升可能不理想。如果某個資源消耗的 gas 量遠高於其他資源，由於其基礎費用相對於需求量較高，其他資源的 gas 使用率可能會遠低於均衡狀態下的目標值。需求量較高的資源則始終保持在 50% 左右的目標值。對於計算等突發性受限的資源，理想情況下應該儘可能接近其極限值，否則大多數區塊中可用的處理能力都會被閒置。

圖 1 2548×2586 199 KB

圖 1.應用max函數計算兩個獨立計量資源計量天然氣時的基本費用變化。根據 EIP-1559 規範，價格變化 0% 表示計量資源的計量量為G=0.5， G = 0.5 ；價格變化 12.5% 表示計量量為G=1， G = 1 ； -12.5 %表示計量量為G=0， G = 0。

需要注意的是， max函數的非線性特性會導致長期消耗量低於目標值。即使兩種資源的長期消耗量達到平衡，在單個區塊層面也未必總是平衡的。因此，價格的設定僅是為了維持利用率較高的資源的目標利用率。例如，如果某些區塊的利用率為(0.5 , 0.3 ) ，而其他區塊的利用率為(0.3, 0.5)，則長期平均利用率可能僅在( 0.4 , 0.4 )左右。

此外，需要注意的是，兩種資源的指定天然氣價格可能無法確保它們都達到指定的“目標”消耗量。這既有利也有弊，可以通過計量過程中的預處理步驟進行調整，如第7節所述。

3. EIP-8075 的平均函數

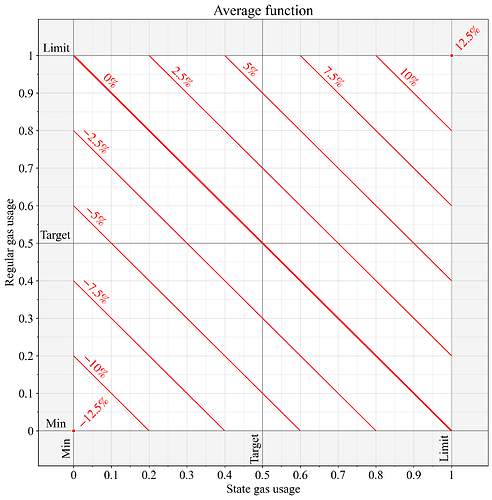
圖 2 展示了計量氣體G 1 和G2 的average ，即兩種獨立資源所用氣體量的平均值。這是EIP-8075的方法（除了其單獨的目標設定步驟）。採用這種計量方法，如果兩種資源在平衡狀態下的利用率不同，則其中一種資源的利用率會被推高至 50% 以上，另一種資源的利用率則會被推低至 50% 以下。具體來說，由於系統在(G 1 + G 2 ) /2=0.5時達到平衡，因此 G 1 + G 2 = 1 。假設利用率的相對差異保持不變，與max函數相比，這種方法能更好地保持尺度不變，因為總消耗氣體量（以歸一化單位計）始終為 1。

另一個好處是，與現在一樣，這兩種資源始終會影響基礎費用。之所以採用動態定價拍賣，首先是為了確定每個區塊的固定價格，同時該價格可以根據需要進行調整，從而將突發性資源（例如常規 gas）的消耗控制在限值內，並將長期性資源（例如狀態增長）的消耗控制在目標水平。為了使狀態增長保持在接近某個特定水平，如果一個區塊消耗了目標水平的常規 gas 和狀態創建 gas，其基礎費用與僅消耗目標水平的常規 gas 而未消耗狀態創建 gas 時的基礎費用有所不同，這似乎是有益的。

圖 2 2548×2586 396 KB

圖 2.應用average函數計算兩個獨立計量資源計量天然氣時的基本費用變化。根據 EIP-1559 規範，價格變化 0% 表示計量資源的計量量為G=0.5， G = 0.5 ；價格變化 12.5% 表示計量量為G=1， G = 1 ； -12.5 %表示計量量為G=0， G = 0。

如果將此方法應用於 EIP-8011，則需要注意一個問題：長期來看，單個資源的使用量可能會接近其極限。當然，如果 EIP-8011 中使用兩個以上的資源，那麼其中一個資源可能會完全達到其極限。而 EIP-8075 同樣使用average函數，因此不存在兩個資源使用量受限的問題，因為狀態創建 gas 成本會迅速調整，使兩個資源的利用率都恢復到 50% 的平衡狀態。

4. 介於`max`和`average`之間的解

max和average函數關注點不同，可以通過將結果置於兩者之間來解決。這樣既能更好地保持可擴展性，又能防止在分佈不平衡的情況下，資源長期接近其極限。

4.1 `max`和`average`的加權組合

一個簡單的解決方案是對兩種資源G_1 G 1和G_2 G 2的已用 gas 進行加權平均，即max和average的加權平均值：

G = (1-w) \max(G_1, G_2) + w(G_1 + G_2)/2。

G = ( 1 − w ) max ( G 1 , G 2 ) + w ( G 1 + G 2 ) / 2.

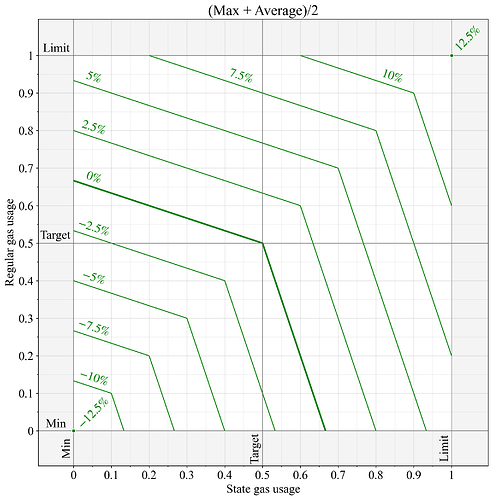
w的兩個可能取值是 1/2 和 2/3。圖 3 顯示了w=1/ 2時的結果，此時完整的方程變為：

G = \frac{\max(G_1, G_2) + (G_1 + G_2)/2}{2}.

G = max ( G1 , G2 ) + ( G1 + G2 ) / 2 。

圖 3 2548×2586 461 KB

圖 3.應用max和average函數的加權組合 ( w=1/ 2 )計算兩個獨立計量資源的計量天然氣時，基本費用的變化。根據EIP-1559規範，價格變化 0% 表示計量資源的計量值為G=0.5，12.5 % 的價格變化由G = 1產生， -12.5 %則表示G = 0 。

4.2 歐幾里得範數

更精細的解決方案是採用歐幾里得範數（L2 範數）：

G = \sqrt{\frac{G_1^2+G_2^2}{2}}.

G = √G21 + G222 。

這樣就形成了一個平滑的表面（四分之一圓），其中每種資源對計量天然氣的邊際影響與其當前使用量成正比：

\frac{\partial G / \partial G_1}{\partial G / \partial G_2} = \frac{G_1}{G_2}.

∂G / ∂G 1 ∂G / ∂G 2 = G1 G2 。

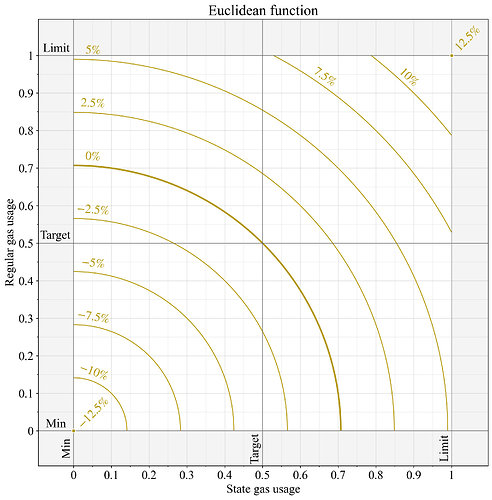
如果當前使用量滿足G_1 = 2G_2， G_1 = 2G_2 ，那麼額外增加一個單位的常規氣體，計量氣體的增加量大約是額外增加一個單位的狀態生成氣體的兩倍。因此，該機制對運行量遠高於其目標值的特定資源最為敏感，同時始終會受到兩種資源消耗量變化的影響。另一個有趣的特性是，當歐幾里得範數在接近目標交點運行時，在區塊級別上產生的變異阻力非常小。歐幾里得範數還具有直觀的幾何特性，它將計量氣體量衡量為到原點的距離。圖 4 展示了這一函數。

圖 4 2548×2586 454 KB

圖 4.應用歐幾里得範數計算兩個獨立計量資源計量天然氣時的基本費用變化。根據 EIP-1559 規範，價格變化 0% 表示計量資源的計量值為G=0.5， G = 0.5 ；價格變化 12.5% 表示計量值為G=1， G = 1 ； -12.5 %表示計量值為G=0， G = 0。

從概念上講， max 、 average和歐氏範數都可以用以下方程式表示。

G = \left(\frac{G_1^p+G_2^p}{2}\right)^{1/p}.

G = ( G p 1 + G p 2 2 ) 1 / p 。

對於平均函數， p=1， p = 1 ；對於歐幾里得範數， p=2， p = 2 ；對於最大值函數，p趨於無窮大。

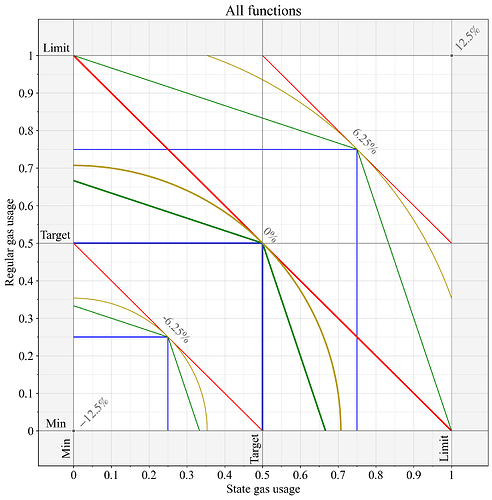
4.3 所有函數的聯合圖

圖 5 將圖 1-4 中的結果彙總在一起，以便於比較。所有計量氣體方程在兩種資源均等使用時均得出相同的結果，但在應對資源利用不平衡的情況時則有所不同。

圖 5 2548×2586 434 KB

圖 5.圖 1-4 的基本費用變化在同一張圖中呈現。

5. 不對稱的目標/極限比率

5.1 動機

非對稱的目標/限制比率也是可行的。由於狀態增長不受突發限制，因此相對於目標而言，更高的限制可能是有益的。相反，由於常規 gas 受突發限制，理想情況下，其目標和長期平均消耗量應該更接近其限制，就像現在的 blobs 一樣。如前所述，在average函數下，如果目標超過限制的一半，而另一種資源未使用，則可能導致其中一種資源完全達到其限制。因此，在計算平均值時，不應提高目標/限制比率，實際上降低該比率可能更可取。

對於其他函數，可以提高突發約束資源的目標/限制比率。這樣做的一個動機是，一個資源的利用率高於目標值會降低另一個資源的均衡利用率。目標利用率只是max函數的一個上限——如果一個資源的利用率高於預期，則在均衡狀態下，一個資源的實際利用率可能接近於零。此外，如第 2 節所述，區塊級別的不均衡利用也會降低均衡利用率。因此，如果兩個資源的需求量相等， max函數會認為兩個資源的利用率都低於目標值。

5.2 非對稱最大值

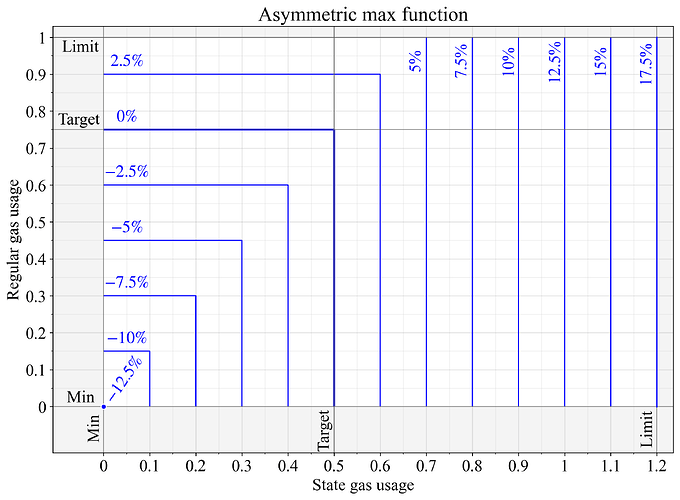
圖 6 中的非對稱max函數顯示了規則氣體目標位於中點上方 1/4 處（極限的 3/4 處），這是通過應用預處理G'_1 = \frac{2}{3}G_1 G ′ 1 = 2 3實現的。G1 。此預處理使得G1 = 3 / 4重置為(3/4)×(2/3)=1/ 2，即在應用max函數之前， ( 3/4 ) × ( 2/3 ) = 1 / 2 。由於此資源不受突發限制，狀態gas的上限提高了20%。

圖 6 2548×1873 206 KB

圖 6.在非對稱max函數下的基本費用變化，該函數將常規氣體的目標設定為其限制的 3/4，並將狀態氣體的限制擴大 20%。

5.3 非對稱歐幾里得範數

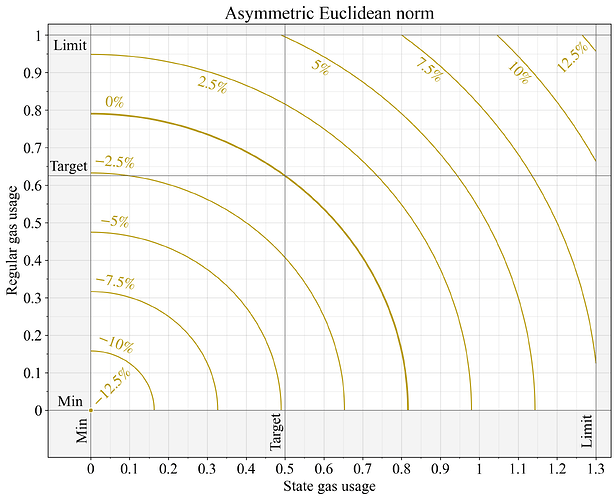
在圖 7 所示的非對稱歐幾里得範數下，常規氣體目標位於中點上方 1/8 處（即T_1=5/ 8處）。應用線性預處理步驟，使得常規氣體和狀態氣體各一個邊際單位在目標交點(T_1,T_2 )處的影響相等。考慮預處理後的歐幾里得計量方程：

G = \sqrt{\frac{(c_1G_1)^2+(c_2G_2)^2}{2}}.

G = √ ( c₁G₁ ) ² + ( c₂G₂ ) ² 。

目標點處的邊際影響相等意味著∂G/∂G_1 = ∂G / ∂G_2 ∂G / ∂G_1 = ∂G / ∂G_2在( T_1 , T_2 )處成立，簡化後為

c_1^2T_1 = c_2^2T_2\qquad\Rightarrow\qquad\frac{c_1}{c_2}=\sqrt{\frac{T_2}{T_1}}.

c 2 1 T 1 = c 2 2 T 2 ⇒ c1 c2 = √T2T1 。

c_1和c_2的值被設定為滿足G(T_1,T_2)= T_2 ，因為T_2保持不變，為1/2 。這是在以下情況下實現的：

c_2 = \sqrt{\frac{2T_2}{T_1+T_2}}, \qquad c_1 = \sqrt{\frac{T_2}{T_1}} \sqrt{\frac{2T_2}{T_1+T_2}}.

c 2 = √ 2 T 2 T 1 + T 2 ， c 1 = √ T 2 T 1 √2T2T1 + T2 。

由於狀態氣體不受突發限制，因此其上限進一步提高了 30%。

圖 7 2548×2066 433 KB

圖 7.在非對稱歐幾里得範數下的基本費用變化，其中普通天然氣的目標值設定為其極限值的 5/8，並將國有天然氣的極限值擴大 30%。對測量的天然氣值進行預處理，確保在目標交點(T_1,T_2) 處，一個邊際單位的普通天然氣和國有天然氣具有相同的影響。 ( T1 , T2 ) 。

6. 多維氣體核算

為了保持（部分）可擴展性，最簡單的機制是沿用當前的 EIP-1559 機制，但在計算區塊累計 gas 使用量時，略微減少每個狀態 gas 單位的計算。用戶仍然需要支付狀態 gas 的全價。因此，發送方支付的gas_used計算方式與正常情況相同： gas_used = regular_gas_used + state_gas_used 。但是，在計算區塊的cumulative_gas_used時，會應用一個DISCOUNT_FACTOR （例如， DISCOUNT_FACTOR = 2 ），該折扣因子將計入區塊的 gas 限制。


 cumulative_gas_used = regular_gas_used + state_gas_used // DISCOUNT_FACTOR

因此，該協議無需分別聚合兩種資源來應用計量氣體方程，因為它並不試圖維護不同的限制。當然，這也不利於擴展性，因為在平衡狀態下，狀態氣體仍然會（在一定程度上）擠佔常規氣體的份額。

7. 結論

7.1 可行方案的比較

針對 EIP-8037 研究了幾種不同的計量 Gas 方程。在一種極端情況下，計量 Gas 可以計算為兩種資源消耗量的max 。如果目標值是限制值的一半，那麼在均衡狀態下，一種資源的消耗量可能會非常低，因為需求量較高的資源在長期內無法超過其目標值。為了彌補這一點，如果重新定價後狀態創建的需求遠超預期，則可以將目標值調整得更接近突發約束常規 Gas 的限制值，以保持可擴展性。

另一方面，計量氣體可以計算為兩種資源的average 。當一種資源的需求量相對高於另一種時，其長期使用量可以略有增加，從而使使用量較低的資源在均衡狀態下不至於被壓得太低。然而，如果普通氣體比狀態生成氣體更受歡迎，那麼普通氣體的目標值就不能不對稱地設定得更接近其極限值，因為長期均衡使用量可能已經接近於1。

可以通過加權平均值或歐氏範數來計算兩種極端情況之間的折衷方案。這些折衷方案允許目標/限制比率不對稱，但比使用max函數時更為保守。

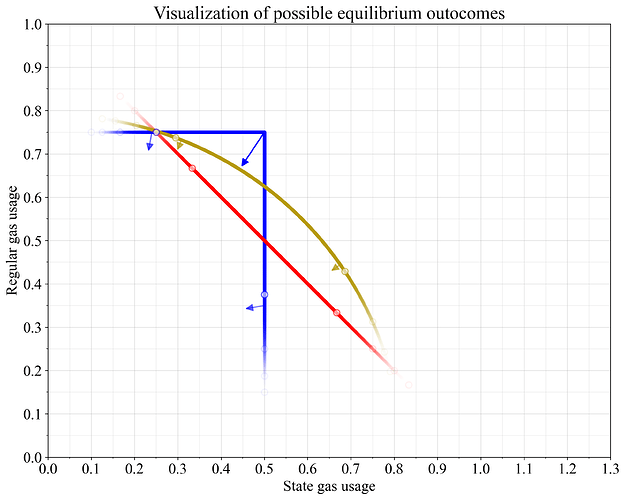
圖 8 展示了之前在圖 2、圖 6 和圖 7 中呈現的所有三種方案，但僅關注基本費用不變 (0%) 的均衡點。一個重要的方面是，當資源需求與研究人員預先設定的假設存在差異時（尤其是在初始假設兩種資源的需求均達到目標水平的情況下），系統會如何運行。因此，圖中用圓圈標記了兩種資源均衡利用率分別為 {2:1, 3:1, 4:1, 5:1} 時的結果。為了便於可視化，不同線條的透明度採用正態分佈進行設置，比率的每個整數倍增加（每個圓圈）代表一個標準差。

如第 2 節所述， max函數的非線性特性會降低均衡利用率，尤其是在目標交叉點附近。這一特性用箭頭表示。對於接近目標交叉點的max函數，這種影響最為顯著。而對於平均函數，區塊層面的不匹配則會導致長期利用率沿著 0% 線移動，而不是垂直於該線。

圖 8 2587×2066 252 KB

圖 8展示了本文研究的計量氣體方程可能出現的結果。圓圈表示當一種資源相對於另一種資源的消耗比例分別為 {2:1, 3:1, 4:1, 5:1} 時的均衡結果。箭頭表示在非線性計量氣體方程下，當各個區塊的資源分佈不均勻時，長期利用率會下降。

7.2 需求、目標設定和天然氣限額的變化

EIP-8011 等計量方法存在一個問題，而 EIP-8075 則不存在這個問題，即難以預測價格變化將如何影響需求。無論採用何種計量天然氣方程，研究人員都必須考慮他們認為新的有效天然氣價格將如何影響需求，並據此設計相應的處理流程。

需要注意的是，在特定 Gas 價格下，需求量未必與協議設定的“目標”相符。這裡不存在像 EIP-1559、EIP-4844 或 EIP-8075 那樣的完全“目標設定”，即通過調整價格來確保一定的利用率。如果狀態 Gas 的需求量僅佔常規 Gas 的 3/7，那麼忽略區塊波動，即使狀態 Gas 的消耗量翻倍，在max函數下也不會影響 Gas 價格。為了使狀態 Gas 的計量水平始終能夠影響 Gas 價格（從而構成真正的目標設定），可以採用轉移函數，根據不同的計量水平對 Gas 進行計量和收費。用戶將按規定的 Gas 價格支付交易費用，但max函數可以應用於例如以 7/3 的更高計量水平計量的 Gas。

該策略與第 5 節中針對非對稱比率執行的歸一化步驟有些類似，但隨後也應用於對稱比率下，以補償未達到目標值的需求。然而，這也意味著狀態創建對整體 gas 價格的影響相對於用戶實際支付的 gas 費用而言會過大。考慮到這一點，在需求失衡的情況下，採用比max函數更寬鬆的方案似乎更具吸引力。第 6 節也值得參考，因為它降低了狀態創建 gas 對定價的影響。這種方法也可以應用於例如average函數的情況。

一個相關的問題是如何處理 gas 上限的變化。隨著 gas 上限的提高，狀態創建量也會隨之增加。為了控制狀態創建量，一種解決方案是根據 gas 上限的變化調整其 gas 價格，例如，如本文所述。正如難以預測一次性重新定價對需求的影響一樣，預測這種漸進式變化的影響也同樣困難。當 gas 上限翻倍時，狀態創建的 gas 價格並非簡單地翻倍即可。正確的調整取決於需求彈性，而目前很難對此進行預測。然而，當然可以盡力嘗試，然後在下一次硬分叉時根據觀察到的彈性進行調整。這通常是多維計量下必須採取的方法，涉及初始硬分叉中做出的許多假設。