解析 DeGate 採用的零知識證明技術 Groth16

與其他 zk-SNARK 相比，Groth16 具有相對較小的證明大小和快速的驗證時間，這使其非常適合 DeGate 對高效和安全交易處理的要求。

撰文：Carlos Ramos

DeGate 是一個建立在以太坊上基於零知識（ZK）技術的去中心化交易協議。作為一個 ZK Rollup 去中心化交易所（DEX），DeGate 提供類似於熱門中心化交易所（CEX）如幣安或 Bybit 的交易體驗。該協議支援多種功能，包括現貨交易和網格交易，並將不斷新增更多功能以確保交易體驗的流暢性。DeGate 的設計目的是使得交易快速的同時費用低廉，為使用者獲取各種資產代幣時提供更高效和便捷的交易。

在本文中，我們將深入探討 DeGate 的架構以及其背後的零知識和 Groth16 技術。

DeGate 的技術架構

DeGate 的核心技術是零知識彙總（ZK-Rollup），它包含一些鏈上和鏈下元件。賬戶和資產變動在鏈下進行處理，並被彙總到鏈上智慧合約中。

鏈上元件

DeGate 智慧合約是鏈上元件。該智慧合約部署在以太坊區塊鏈上，任何想與交易所進行互動的人都可以訪問。這使得交易變得無需信任且透明，使用者對其資金擁有完全控制權，其資產可以在完全不依賴於 DeGate 的情況下自行取出（參照 Exodus 模式）。在 EVM 網路上部署的智慧合約儲存資產，驗證零知識證明，並提充值和提現的方法。

鏈下元件

DeGate 還利用鏈下訂單撮合和訂單簿管理來降低交易成本並提高交易執行速度。這得益於 zk-rollups 技術，它允許快速高效地處理大量的交易，而無需給以太坊網路增加負擔，同時保持安全和無需信任。

DeGate 鏈下節點主要包括：

• 交易系統：處理使用者的訂單，在訂單簿中進行訂單匹配，處理帳戶和資產狀態變化的事件。
• Operator：定期處理鏈下帳戶和資產交易，生成 zkBlock，呼叫 zkp-worker，提交證明（zkBlock 資料）。
• zkp-worker：描述需要零知識證明的事件，並生成零知識證明。 默克爾樹：以樹形結構儲存 DeGate 協議的帳戶、資產和訂單。
• 鏈同步：觀察和確認在 DeGate 智慧合約內發生的所有交易。
• Postman：在 EVM 網路上呼叫 DeGate 智慧合約方法，並向智慧合約提交 zkBlock 資料。

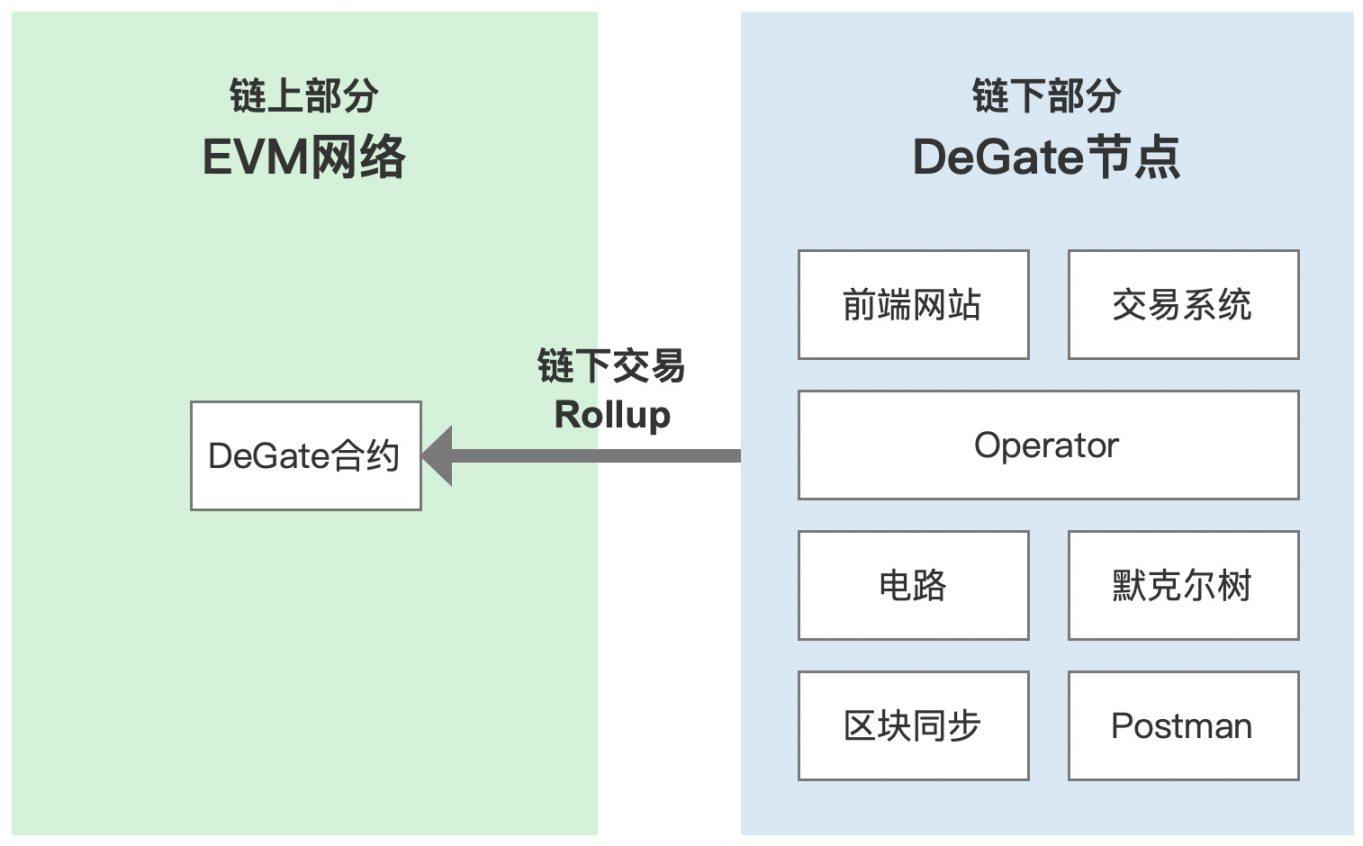
ZK-Rollup 技術

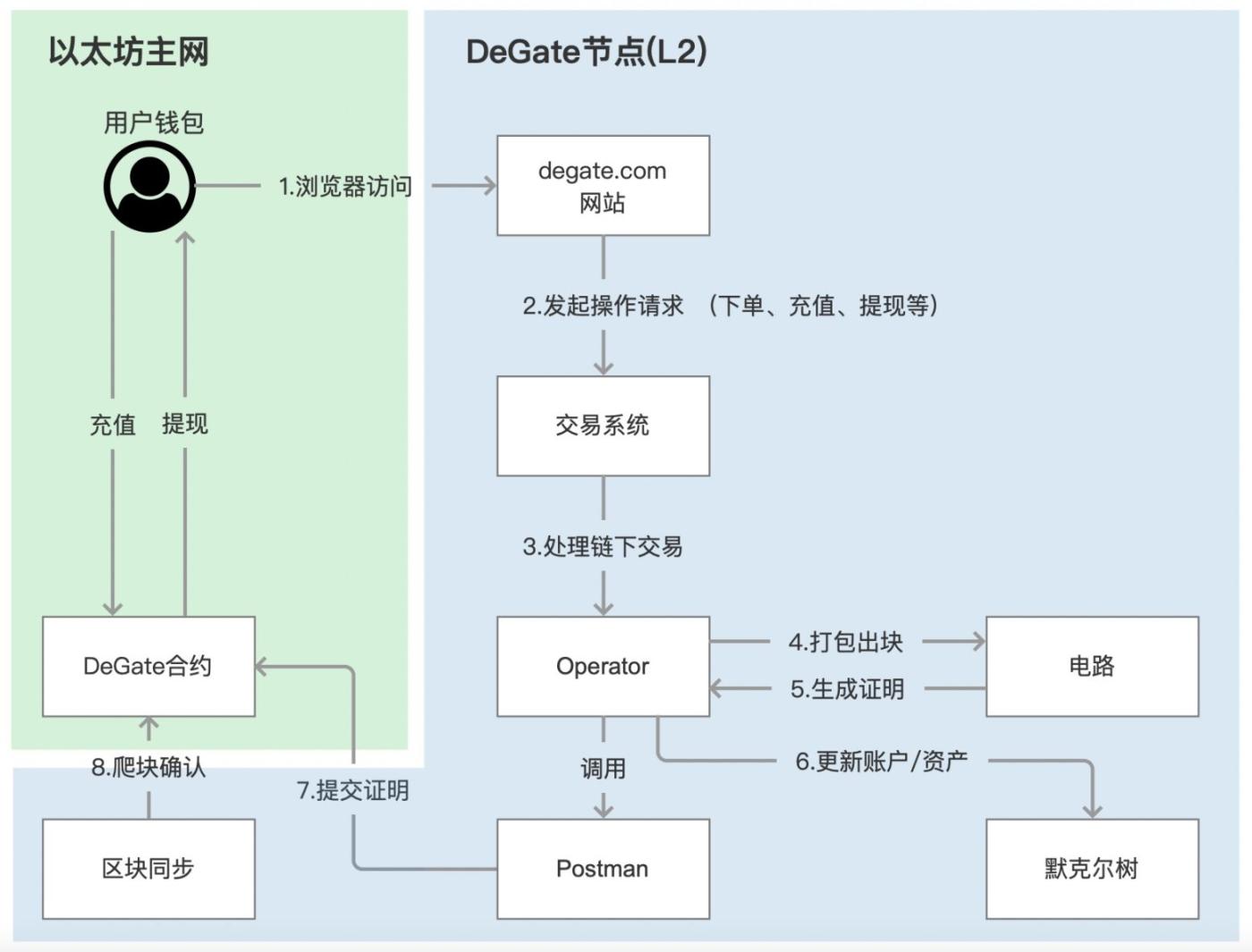
從前面的圖中，我們可以看到 DeGate 有一個名為 DeGate Node L2 的主要元件，而 Rollup 過程可以總結為以下三個步驟：

1. 使用者簽署請求，可以通過 DeGate 使用資產私鑰（PK）或使用者錢包 PK（轉賬、存款）完成。
2. 節點驗證並處理使用者請求，將鏈下交易分批打包成區塊，並呼叫電路生成零知識證明。
3. 節點將證明結果傳送給鏈上智慧合約進行驗證，完成 ZK-Rollup 並實現資料可用性。

資料可用性

DeGate 的 ZK-Rollup 由兩個關鍵因素來保障：證明生成和證明驗證。在 DeGate 協議中，證明生成由節點通過鏈下電路程式來完成。中繼器收集大量交易以生成 SNARK 證明。SNARK 證明是一種類似雜湊的內容，表示對 DeGate 狀態的更改集。為了實現和證明區塊鏈系統的去中心化信任，DeGate 使用開源智慧合約和固定的驗證金鑰進行驗證。

電路程式

關於電路：零知識證明的電路是由一些邏輯閘組成的邏輯電路。任何計算都可以描述為算術電路。基於這個前提，複雜的邏輯操作可以被分解並用簡單的加法和乘法門來描述。

零知識證明（Zero Knowledge Proof）是一種協議，使得一個參與方（證明者）可以說服另一個參與方（驗證者）某個陳述為真，而無需透露任何關於該陳述的資訊。非互動式零知識證明（NIZK）是一種特定型別的零知識證明，其中證明者可以在與驗證者無需互動的情況下生成證明。NIZK 協議非常適用於以太坊應用，因為它們允許智慧合約充當驗證者。這樣，任何人都可以生成一個證明，並將其作為交易的一部分傳送給智慧合約，智慧合約可以根據證明的有效性執行某些操作。在這個背景下，最受歡迎的 NIZK 是 zk-SNARK（零知識簡潔非互動知識證明），它是一組非互動式零知識協議，具有簡潔的證明大小和亞線性的驗證時間。這些協議的重要性體現在兩個方面：一方面，它們有助於提高隱私保護程度，另一方面，它們是解決可擴充套件性問題的可能解決方案，因此非常適合 DeGate 的架構。

像大多數零知識證明（ZKP）一樣，zk-SNARK 允許證明計算性陳述。例如，可以證明以下事實：與特定公鑰相關聯的私鑰的知識，交易的正確計算，或特定雜湊的原像的知識。重要的是，可以在不洩露有關這些陳述的任何資訊的情況下進行這些操作。換句話說，不洩露任何關於私鑰、交易細節或原像值的資訊。更具體地說，zk-SNARK 允許證明可以用算術電路模擬的任何計算性陳述，這類電路通常稱為 zk-SNARK 電路。值得一提的是，大多數 zk-SNARK 協議（例如 Pinnochio、GGPR13 和 Groth16）的實現使用橢圓曲線密碼學。

詳細介紹 Groth16

Groth16 是一種使用橢圓曲線實現的零知識證明系統，可實現對涉及算術電路的計算的高效驗證。該構造基於以下元件：

1. G1 和 G2 兩組點之間的雙線性配對 e：G1 x G2 -> GT，G1，G2 為相關橢圓曲線上一些點的集合，兩個點集的大小都為 r；GT 為對應有限域的乘法群。
2. 公共參考字串（CRS），它是一組提前生成並在證明生成和驗證過程中使用的公共引數。
3. 描述待證明計算的電路 C(x)，其中 x 是電路輸入的向量。 Groth16 構造包括三個階段：金鑰生成、證明生成和驗證。

Groth16 構造涉及多個數學公式和概念，包括橢圓曲線、雙線性配對函式和零知識證明。

Groth16：可信設定

在 Groth16 中，可信設定過程涉及生成用於證明生成和驗證過程的公共參考字串（CRS）。CRS 是一組提前生成並分發給所有相關方的公共引數。該過程涉及生成隨機值，這些隨機值用於以一種確保無法預測或操縱的方式建立 CRS 的公共引數。用於生成公共引數的私有值隨後被銷燬，以防止它們被用於損害系統的安全性。可信設定過程對於確保系統的安全性和完整性至關重要。

Groth16：QAP 和 FFT

在 Groth16 中，證明生成過程涉及建立表示待證明計算的二次算術程式（QAP）。然後，使用快速傅立葉變換（FFT）演算法對 QAP 進行轉換，以建立可在證明中使用的計算的簡潔表示。

QAP 將待證明計算表示為一組二次方程組，其中變數是計算的輸入和中間值。然後，使用 FFT 演算法對 QAP 進行轉換，建立表示計算的多項式承諾，以簡潔形式表示計算。該多項式承諾隨後用於證明驗證計算的正確性。

Groth16 中使用的 FFT 演算法基於 Cooley-Tukey 演算法，該演算法是計算序列的離散傅立葉變換（DFT）的廣泛使用演算法。Cooley-Tukey 演算法用於對 QAP 執行 FFT，將其轉換為比原始 QAP 小得多的多項式承諾。

在 Groth16 中使用 QAP 和 FFT 可以實現對涉及算術電路的計算的高效生成和驗證的零知識證明。使用 FFT 可以減小證明的大小，使得計算和驗證更加高效，而使用 QAP 則允許更自然地表示待證明的計算。

Groth16：ALT_BN128

曲線 ALT_BN128 是一種已知的橢圓曲線。以太坊的 EIP196 和 EIP197 中已新增了此曲線的預編譯合約，這使得通過使用該曲線進行鏈上計算可以節省更多的 gas。

ALT_BN128 曲線是基於配對的密碼學的流行選擇，也是以太坊最早支援，廣泛使用的配對曲線。DeGate 將其用於協議中有效驗證交易。以下是 ALT_BN128 曲線與一些在區塊鏈應用中常用的其他曲線的比較：

1. secp256k1：secp256k1 曲線在區塊鏈應用中廣泛使用，包括比特幣。它由方程 y^2=x^3+7(mod p) 定義，其中 p 為 2²⁵⁶-2³²-2⁹-2⁸-2⁷-2⁶-2⁴-1，是一個 256bit 的大素數。secp256k1 曲線在某些操作上比 ALT_BN128 曲線更快，但不適用於 FFT 計算，因此不被採用在 zk-SNARK 方案中。

2. BLS12-381：BLS12-381 曲線是基於配對的密碼學的另一個流行選擇，用於幾個區塊鏈應用，包括 Zcash。它由方程 y^2=x^3+4(mod p), 其中 p=2^381-3。BLS12-381 曲線在某些操作上比 ALT_BN128 曲線較慢，但具有更高的安全強度。

DeGate 中的 Groth16 和 ZK 區塊大小

在經過大量的研究和討論後，DeGate 最終選擇了 Groth16 作為其 zk-SNARK 協議。Groth16 被 Zcash 等許多著名項目廣泛使用，並且具有豐富的程式實現庫，使其對開發人員友好。它還使 DeGate 能夠在較高的安全強度下實現快速的證明生成和較低的 ZK-Rollup 成本。

DeGate 將鏈下交易打包成 zk 區塊並提交到區塊鏈上。zk 區塊中的交易數量在部署之前根據 ALT_BN128 曲線支援的約束數量和 FFT 計算的難度來確定。zk 區塊中交易數量越多，問題就越複雜，R1CS 電路約束的數量也越大。為了確保 zk 區塊的高效和安全處理，DeGate 確定了幾個具有特定交易數量的 zk 區塊大小。這些大小的範圍從 5 到 355 個交易不等，不同的大小對應不同的 PK 和 VK 集合，目前，DeGate 生成的 zk 區塊具有以下大小：355、300、250、200、150、100、50、25、10。

可信設定

當 DeGate 協議部署到以太坊主網時，電路和智慧合約都會進行初始化。這個過程也被稱為可信設定，涉及到隨機熵。DeGate 協議的可信設定分為兩個階段：

1. 參考 Power of Tau 配置作為初始值。
2. 基於初始值，首先引用未來的比特幣區塊雜湊，然後獲取 5 個社群成員提供的隨機熵，再引用另一個未來的比特幣區塊雜湊。最後，計算並儲存一個 Proving Key 和一個 Verifying Key，分別儲存在電路和智慧合約中。

Groth16 與其他方案的比較

以下是 Groth16 與其他一些流行的和現代化的 zk-SNARK 構造在證明大小和驗證時間方面的比較：

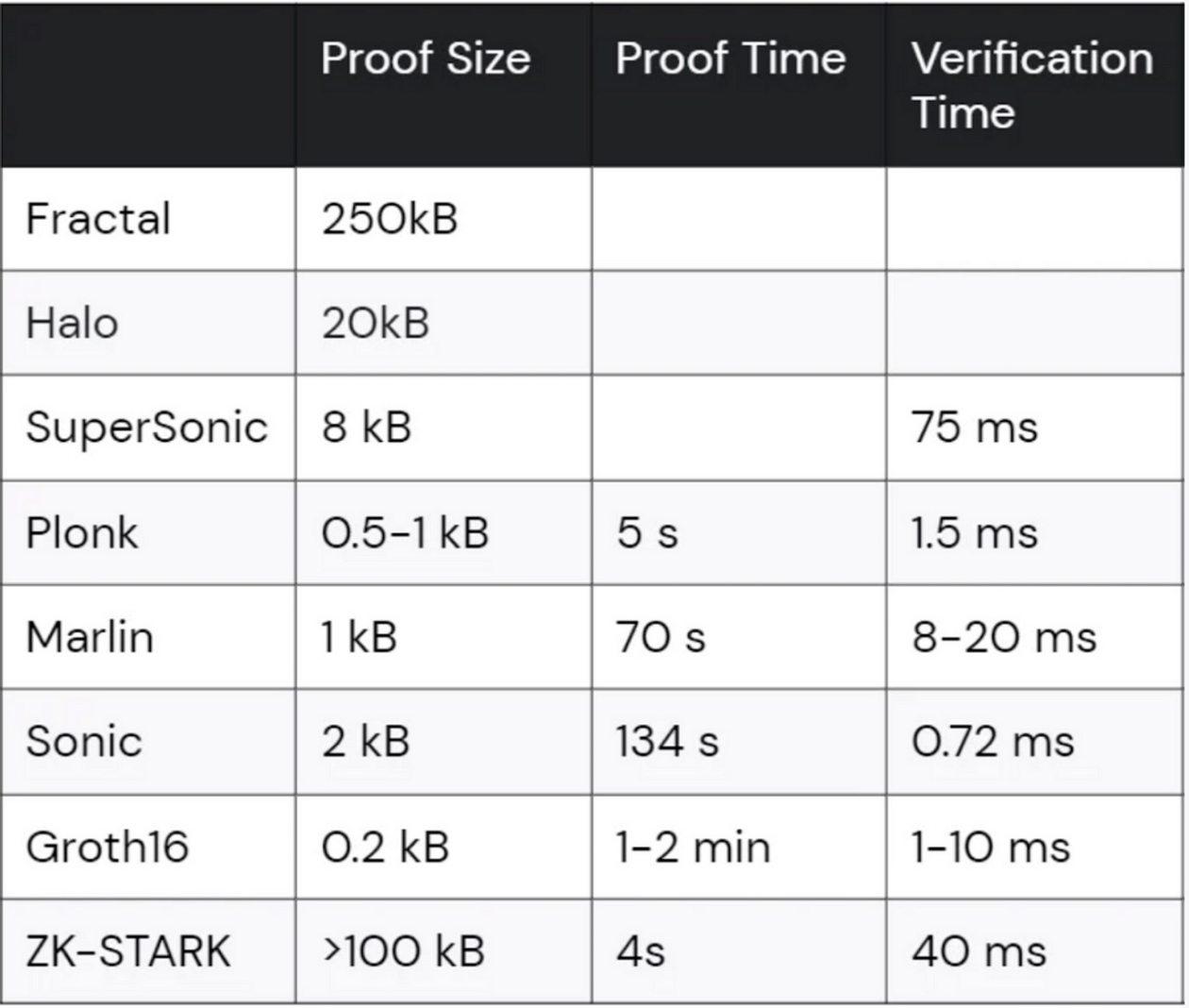
參考來源：https://www.cth.group/insights/page/zk/

GROTH VS PLONK

雖然 Groth16 和 PLONK 都是高效的 zk-SNARK 構造，它們在設計和實現上有一些關鍵區別。

• 易解釋性：Groth16 被認為比 PLONK 更透明，因為它涉及的演算法原理更為直觀，更容易理解和審計。PLONK 涉及更復雜的數學運算和約束過程，這可能使得驗證實現的正確性更加困難
• 證明的大小：Groth16 的證明僅為 3 個群元素，而 Plonk 的證明大小在同等條件下一般是 Groth16 的 2.5 倍左右
• 驗證計算量：Groth16 驗證時需要的配對計算多於 PLONK；特別的，在對 k 個證明做批量驗證時，Groth16 需要做 (k+3) 次配對，而 PLONK 的驗證都是可以合併的，始終只有 2 次配對計算
• 靈活性：Groth16 採用 CRS，每次電路改變都需要重新做 trusted setup；PLONK 採用 SRS，電路結構變化並不需要重新做 setup，更適應多樣化的任務和需求

總體而言，當一個應用程式需要為同一電路生成多個證明（例如單個邏輯計算）且儲存相關效能至關重要時，Groth16 是最合適的選擇，而當一個應用程式需要處理許多不同的電路（例如可快速更新的業務邏輯）且保持高效能時，PlonK 是較為合適的選擇。

DeGate 的零知識證明方案選擇

DeGate 選擇 Groth16 是因為它具有高效和安全的特性。與其他 zk-SNARK 構造相比，Groth16 具有相對較小的證明大小和快速的驗證時間，這使其非常適合 DeGate 對高效和安全交易處理的要求。Groth16 還具有簡單易懂的優勢，有助於進行安全審計和測試。

因此，對於 DeGate 來說，Groth16 是目前一種較為合適的 zk-SNARK 構造，因為它提供了在以太坊區塊鏈上處理交易所需的效率、安全性和簡潔性，但我們選擇的技術也是為了產品和使用者服務，所以基於下面幾個特點會考慮各種先進 ZK 方案的採用和創新

• 效率：根據 DeGate 產品概述，該協議設計用於處理高達 355 筆交易的區塊。Groth16 非常適合這個任務，因為它已被證明在基於配對的密碼學中非常高效，而在 zk-SNARK 中廣泛使用了配對操作。
• 安全性：正如前面提到的，Groth16 被認為非常安全，並且在區塊鏈應用中有著強大的使用記錄。這對於 DeGate 非常重要，因為它涉及處理金融交易並需要高水平的安全性。
• 效能：Groth16 的驗證時間在典型 CPU 上約為 10 毫秒，比其他 zk-SNARK 構造要快得多。此外，Groth16 的證明大小相對較小，這意味著在區塊鏈上需要傳輸的資料更少。這對於 DeGate 非常重要，因為它有助於降低在以太坊區塊鏈上處理交易所需的 gas 成本；另外，為了進一步降低驗證等過程的成本，可以結合 PLONK 方案去提高驗證階段的效能
• 可擴充套件性：為了支援更多的功能，實現可更新的電路結構和快速迭代，Degate 也將會採用 Halo2 等在多樣化任務下更加強大先進的零知識證明方案，在保護使用者隱私和資產安全的基礎上降低交易成本和滿足更多需求

總結

本文對 DeGate 協議及其基礎的 Groth16 證明系統進行了深入分析，解釋了 DeGate 如何利用 Groth16 證明系統建立安全高效的去中心化交易所平臺。重點介紹了 DeGate 架構的各個組成部分，清晰闡述了 DeGate 採用的零知識證明技術。