0xAlpha 投稿 DODO research:讓我們一起深入解析了 zk-SNARK 技術,探討它在加密和區塊鏈中實現隱私保護的原理和應用
作者:0xAlpha Co-founder @DeriProtocol
歡迎關注推特:@0x_Alpha

0xAlpha 投稿 DODO research。這篇文章將用數學解碼這項技術,揭示它如何在不透露任何信息的情況下證明知識的真實性。準備好,讓我們一起揭開 zk-SNARK 的神秘面紗。
介紹
zk-SNARK,即 “零知識簡潔非交互式知識論證”,使得一名驗證者 能夠確認一名證明者 擁有某些特定知識,這些知識被稱為 witness,滿足特定的關係,而無需透露關於見證本身的任何信息。
為特定問題生成 zk-SNARK 包括以下四個階段:
- 將問題(或函數)轉換成算術門電路。
- 然後將這個電路翻譯成矩陣公式。
- 這個矩陣公式進一步轉換成一個多項式,這個多項式應該能被一個特定的最小多項式整除。
- 最後,這種可整除性在有限域的橢圓曲線點中表示出來,證明就在這裡進行。
前三個步驟僅僅是轉換了原始陳述的表示方式。最後一個步驟使用同態加密將第三步的陳述投影到加密空間中,使得證明者能夠證實其中的鏡像陳述。鑑於這種投影利用了非對稱加密,從第三步的陳述回溯到原始陳述是不可行的,確保了零知識的暴露。
閱讀本文所需的數學背景相當於 STEM 專業學生的大一級代數水平。唯一可能具有挑戰性的概念可能是橢圓曲線加密。對於不熟悉這一點的人來說,可以將其視為具有特殊基數的指數函數,同時要記住其逆函數仍然未解。

在本文中,我們將繼續使用方程式 (1) 作為討論的基礎。
第 1 步:算術門電路
方程式 (1) 可以分解為以下基本算術運算:
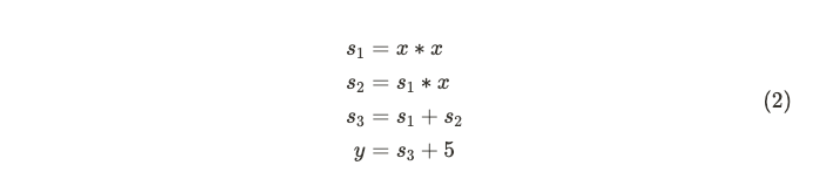
這對應於以下算術門電路:
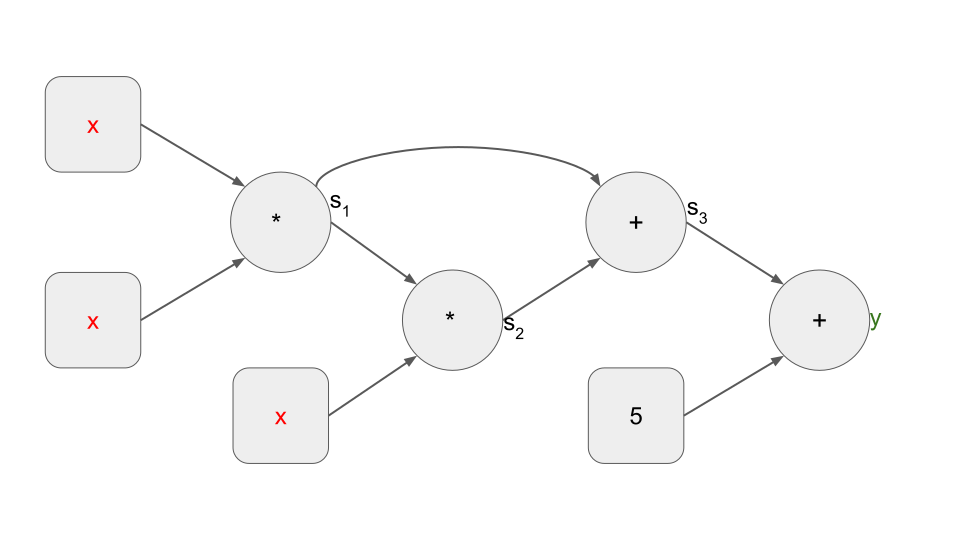
我們還將方程式 (2) 稱為一組 4 個 “一級約束”,每個約束描述了電路中一個算術門的關係。通常,一組 n 個一級約束可以概括為一個二次算術程序(QAP),接下來將進行解釋。
第 2 步:矩陣
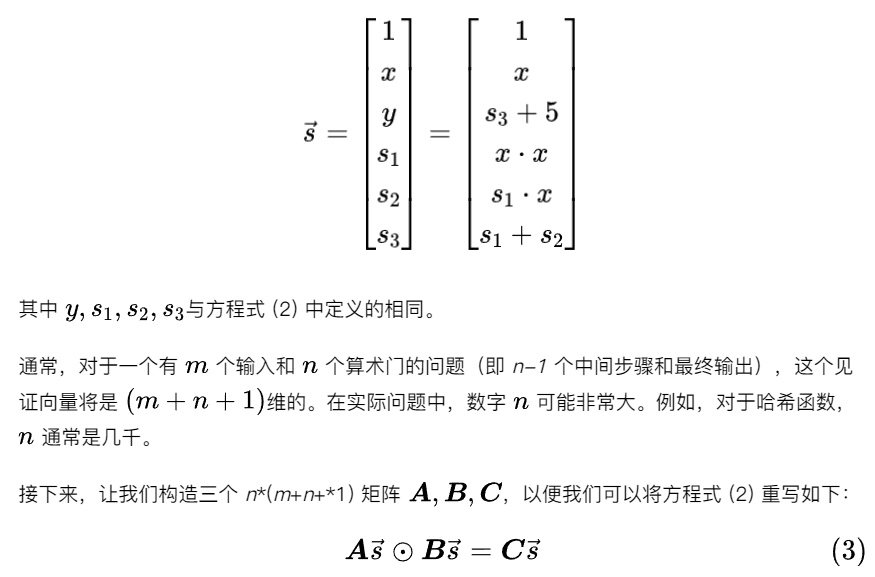
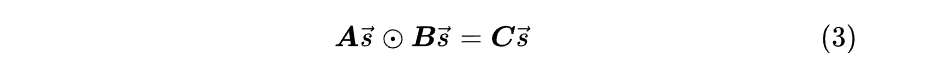
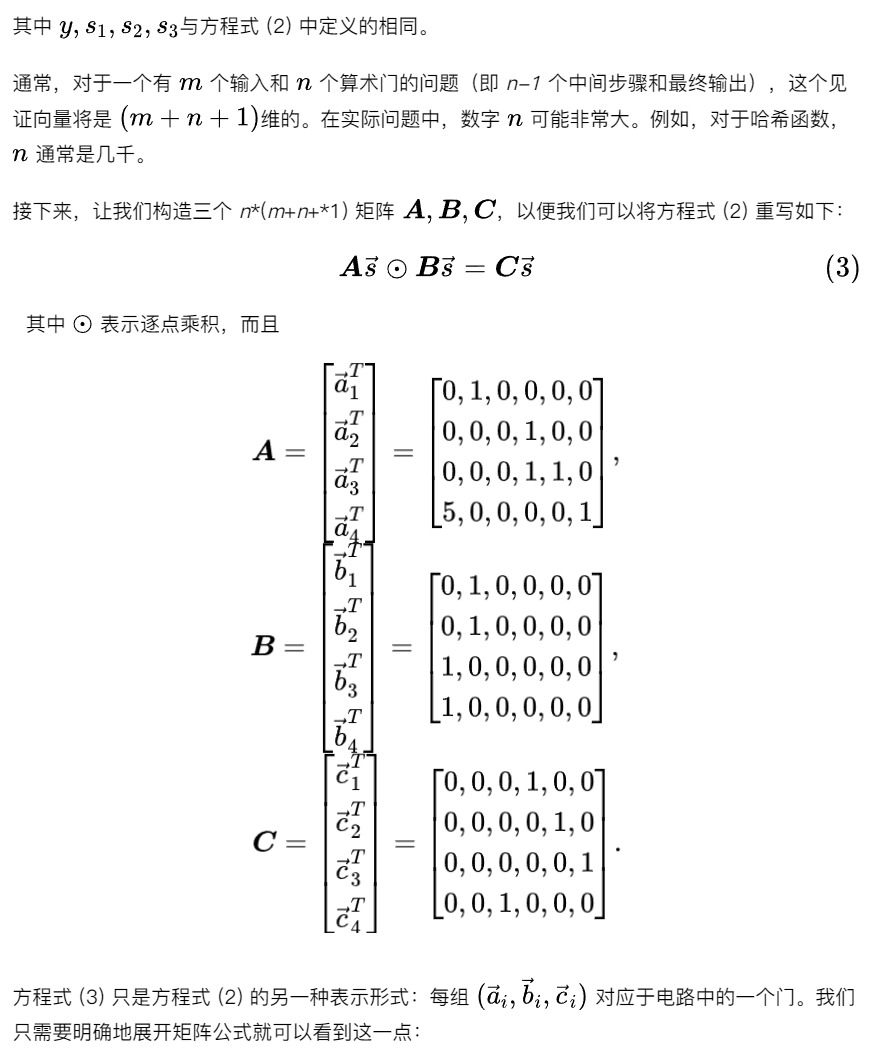
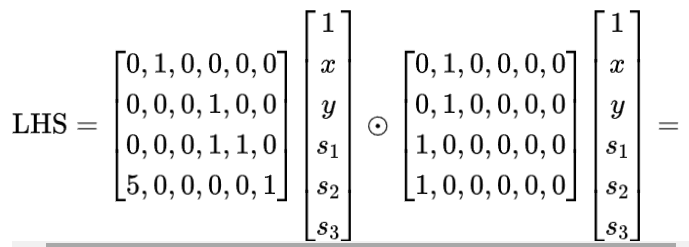
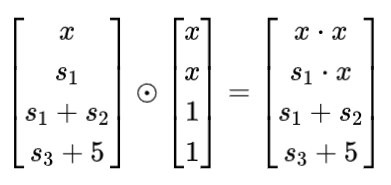

第 3 步:多項式

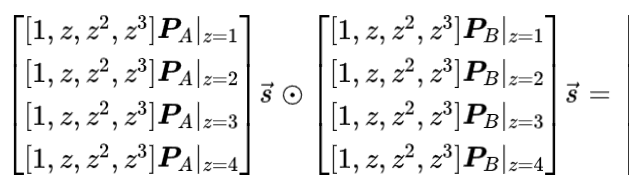
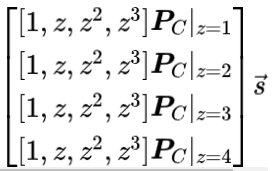
如果提取出每一行單獨觀察,不難發現這四行對應於在四個點分別求值的相同表達式。因此,上述矩陣方程等價於:

一種直接但不保密的方式來證明這一點是提供方程式 (4) 的左邊並展示因式分解。然而,zk-SNARK 的主要目的是保持隱秘(不透露任何知識)。因此,我們不會直接證明這個方程,而是在橢圓曲線點的空間中證明它的加密版本。
第 4 步:橢圓曲線點
將方程式 (4) 重寫為:

接下來,我們將更詳細地闡述實際的操作步驟。
橢圓曲線加密

另一方面,兩個橢圓曲線點的加法定義如下圖所示:
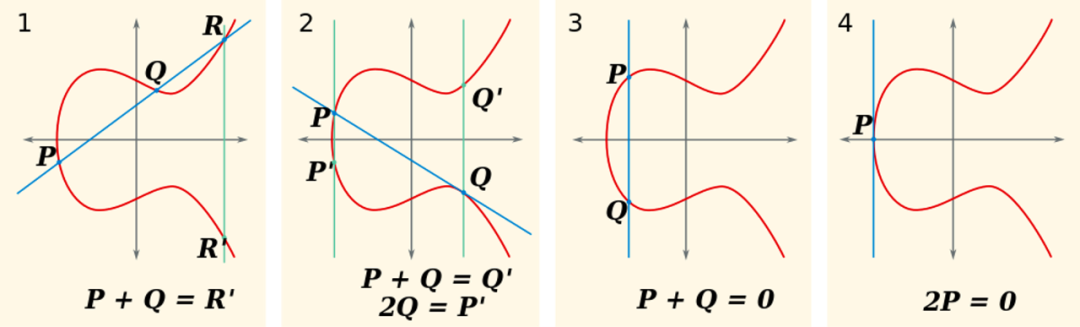


然而,Alice 想要證明的方程式 (5) 是二次形式的,所以線性不夠。為了處理二次項,我們需要在加密空間中定義乘法。這被稱為配對函數,或雙線性映射,接下來將進行解釋。
雙線性映射

這是我們都熟悉的東西——加法和乘法操作的分配律。
有了這樣的雙線性映射,我們就可以將方程式 (5) 的兩邊映射到加密空間。
公共參考字符串

整個過程被稱作 “驗證鑰”,簡稱 VK。這裡只涉及 7 個橢圓曲線點(ECPs),需要提供給驗證方。要注意的是,不管問題裡面涉及多少輸入和一級約束,VK 始終是由 7 個 ECPs 構成的。
另外,值得一提的是,“可信設置” 以及生成 PK 和 VK 的過程,對於一個特定的問題來說,只需操作一次即可。
證明與驗證
現在擁有公鑰(PK),愛麗絲將計算以下橢圓曲線點(ECPs):
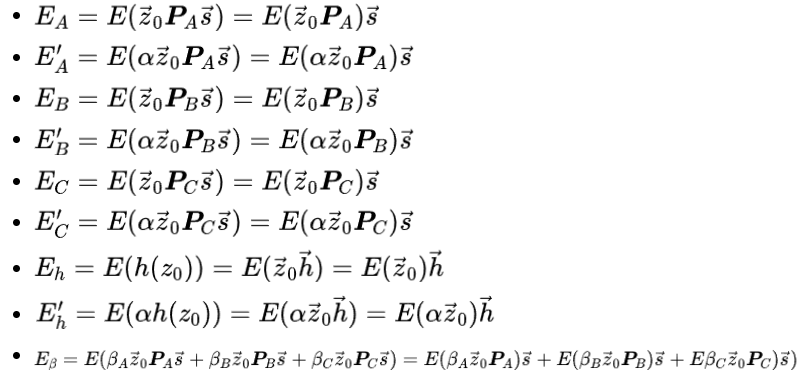
這 9 個橢圓曲線點就是零知識簡潔非交互式證明(zk-SNARK)的關鍵!
注意,愛麗絲其實只是對公鑰裡的橢圓曲線點做了些線性組合運算。這點特別關鍵,驗證時會重點檢查。
現在,愛麗絲交出了 zk-SNARK 證明,咱們終於進入驗證環節,分三步走。

參考文獻
- “Zk-SNARKs: Under the Hood” (Vitalik Buterin)
- “A Review of Zero Knowledge Proofs” (Thomas Chen, Abby Lu, Jern Kunpittaya, and Alan Luo)
- “Why and How zk-SNARK Works: Definitive Explanation” (Maksym Petkus)
- Website: Zero-Knowledge Proofs
- Wikipedia: Elliptic curve
- Wikipedia: Finite field
- Wikipedia: Pairing-based cryptography
免責聲明
本研究報告內的信息均來自公開披露資料,且本文中的觀點僅作為研究目的,並不代表任何投資意見。報告中出具的觀點和預測僅為出具日的分析和判斷,不具備永久有效性。
免責聲明:作為區塊鏈信息平臺,本站所發佈文章僅代表作者及嘉賓個人觀點,與 Web3Caff 立場無關。本文內容僅用於信息分享,均不構成任何投資建議及要約,並請您遵守所在國家或地區的相關法律法規。







