作者:Aram Jivanyan、Albert Garreta、Hayk Hovhanissyan、Ignacio Manzur、Isaac Villalobos-Gutiérrez 和 Michal Zajac。
在這篇文章中,我們研究了當一個人必須同時提供許多證明時攤銷成本的問題。我們稱之為“打包”的方法適用於基於 FRI 的 SNARK(例如 ethSTARK、Plonky2、RISC0、BoojumETC)。它允許生成一個證明,證明許多證人滿足某些約束,同時減少驗證者的工作和證明大小(與為每個證人生成證明並由驗證者檢查其中每個證據相比)。我們通過實驗證明該技術在實踐中是有用的。
在即將發表的技術論文中,我們將更深入地研究打包機制,並將討論聚合基於 FRI 的 SNARK 證明任務的其他方法。這項工作在某種程度上可以看作是社區最近為 SNARK 證明任務設計累積方法(例如摺疊方案)所做的努力的延續。然而,在基於 FRI 的 SNARK 環境中,人們面臨著沒有同態承諾方案的不便,這需要與最近開發的方法截然不同的方法。
更詳細地說,打包是一種批量證明生成方法,允許證明者為潛在的不同實例生成證人可滿足性的單一證明。打包帶來的主要改進是證明者和驗證者在所有實例上僅執行一次 FRI 低度測試。與順序證明每個見證人的可滿足性相比,驗證者時間和打包證明的證明大小都減少了,證明者時間略有減少。我們的基準測試表明,對於典型的跡線(216 行,100 列),驗證者時間縮短約 2 倍,證明大小減少約 3 倍。
正如我們稍後解釋的,這種方法與長遞歸證明任務的結合特別相關。例如,當單個證明者遞歸地生成多個見證人有效性的證明時,證明者可以使用“遞歸層”之間的打包來證明有關下一層較小驗證者和較小見證人的陳述。
我們注意到,打包方法可以“聚合”基於 FRI 的 SNARK 證明的潛在不同關係和類型的證明任務。例如,對於兩種語言 L₁、L2 和兩個實例 x₁、x2,打包可以分攤使用 ethSTARK 證明 x₁∈L₁ 的成本,以及使用 Plonky2 證明 x2∈L2 的成本。
在下一節中,我們將簡要概述打包技術及其性能改進。之後,我們討論它的一些潛在應用。我們通過展示實驗結果來遵循這一點。我們推遲了對該技術的正式描述及其相應的健全性分析,以供我們即將發表的技術論文(該論文還將描述進一步的優化技術)。
概述
我們專門討論 ethSTARK [Sta21] 協議(有時稱為 STARK)的方法。然而,該技術可以適用於任何“基於 FRI 的 SNARK”(在 [BGK+23] 的意義上)。回想一下,ethSTARK IOP 遵循下面的藍圖。下面,𝔽表示有限域,𝕂是𝔽的有限擴展。
- 見證者是預言機函數 f₁, …, fₛ: D ⊂ 𝕂→ 𝕂,據說是某個有界次數 d 的多項式。這裡,D 是乘法子群 D₀ ⊂ 𝔽* 的 𝕂 中的陪集。陪集 D 稱為評估域。子群 D₀ 包含大小為 d+1 的子群 H₀=<g>,稱為跡域。後者與 AIR 執行跟蹤的行一一對應。這裡,d是度數界限。我們將 fᵢ(X) 稱為見證圖。
- 約束是函數 fᵢ(X) 中的多項式表達式(以及一些移位 fᵢ(gʲ⋅X))。每個這樣的多項式都應該在整個跡域 H₀(或 H₀ 的子集,但為了簡單起見,我們假設所有約束都在所有 H₀ 上消失)上消失。
- 例如,約束的形式可能為 Q(f₁(X), f2(g⋅X)) = f₁(X)2 + f2(f⋅X)3。那麼,這個表達式應該是一個在 H₀ 上消失的“低次”多項式,這意味著對於所有 h∈ H₀,f₁(h)2=f2(g⋅h)3。
- 接下來,驗證者對用於產生單個約束 C: H → 𝕂 的隨機性進行採樣,作為每個約束的隨機線性組合。我們將 C(X) 稱為DEEP-ALI 約束。例如,如果約束為 Q₁(f₁(X), f2(g⋅X)) 和 Q2(f₁(g2⋅C), f2(X)),則組合約束為映射 C(X) := Q(f₁(X), f2(g⋅X)) + α ⋅ Q2(f₁(g2⋅C), f2(X)),其中 α 是隨機元素。同樣,這個約束被認為是一個在 H₀ 上消失的低次多項式。
- 現在,證明者通過證明 C(X)=Z(X)⋅q(X) 來證明 C(X) 滿足上述性質,其中 Z(X) 是跡域 H₀ 的消失多項式,q( X) 是 C(X) 除以 Z(X) 的商,它應該是低次多項式。為此,證明者向驗證者發送一個關於商圖q(X) 的預言。然後,執行以下檢查:
- 檢查 C(X)=Z(X)⋅q(X) 在從 𝕂 採樣的單個隨機點 ψ(稱為深度查詢點)處是否成立。為了進行此檢查,證明者向驗證者發送映射 q(X) 和 {fᵢ(X)} 在 ψ 和移位 gʲ⋅ ψ 處的評估,我們分別寬鬆地表示 q_ψ 和 {fᵢⱼ}。
- 驗證者現在需要確保接收到的值是正確的,並且映射 {fᵢ(X)}, q(X) 的度數較低。為此,證明者和驗證者使用 Batch-FRI 協議來顯示商 (fᵢ(X)-fᵢⱼ)/(X-gʲ⋅Σ) 和 (V(X)-q_Σ)/(X-Σ ) 是低次多項式。
- 回想一下,Batch-FRI 是一種協議,用於證明映射 h₁, …, hₘ: D\to 𝔽 的集合接近於 ≤ d 次的多項式(更技術地說,Batch-FRI 證明這些映射具有 δ 相關性) Reed-Solomon 代碼 RS[𝔽, D, d+1]) 中的協議。該協議的工作原理是將 FRI 協議應用於映射 h₁、…、hₘ 的隨機線性組合。我們將映射 (fᵢ(X)-fᵢⱼ)/(X-gʲ⋅Σ) 和 (V(X)-q_Σ)/(X-Σ) 的隨機線性組合稱為DEEP-FRI 函數。
我們技術中的主要觀察結果是,通過使用 DEEP-ALI 約束組合和 Batch-FRI 組合的線性,我們可以將不同實例的跨證明代的約束和函數打包到單個組合約束和單個 DEEP-FRI 函數中。換句話說,當生成多個 ethSTARK 證明時,可以從所有單獨的證明中獲取所有 DEEP-ALI 約束的隨機線性組合。然後,證明者和驗證者針對生成的“全局”DEEP-ALI 約束執行上面的步驟 4。
當應用 Batch-FRI 時,我們還必須揭示對批處理圖的評估域 D 的評估。當用 Merkle 承諾實例化時,我們將見證圖和商圖的所有評估打包在同一個 Merkle 葉子中 D 中的同一點(與 [MAGABMMT23] 中類似)。即,按照上面的表示法,默克爾樹中的葉子看起來像 Hash(h₁(a), …, hₘ(a)),其中 a∈D 和 h₁, …, hₘ 是在證明。請注意,這不適用於 Batch-FRI 內輪中的 Merkle 樹。
在下文中,為了滿足 N 個見證人對 N 個實例(這些實例可以是 Plonkish、AIR、RAP 實例ETC)的可滿足性,我們將“順序驗證者”稱為檢查基於 FRI 的證明的驗證者(這些可以是通過使用 Plonky2、ethSTARK、RISC0ETC按順序為每個實例生成。 “打包驗證者”將指檢查 STARKPacked 證明以確保每個見證人同時滿足的驗證者。相同的術語適用於證明者。
計算改進
與順序證明不同實例的可滿足性相反,這種改進主要來自於這樣一個事實:現在 Merkle 承諾樹更少,並且我們只對所有實例的可滿足性執行一個 FRI 證明。發生第一點是因為我們在跨實例的每一輪中將所有相關函數的評估打包在同一個 Merkle 葉子中。正如我們所解釋的,發生第二種情況是因為我們將所有商函數組合成一個 DEEP-FRI 函數。
更具體地說,就證明大小而言,該證明比順序證明包含更少的 Merkle 根承諾。它還包括更少的 Merkle 取消提交路徑,因為在所有打包實例中只執行一次 FRI。然而,對於打包證明者需要發送的功能評估數量,沒有攤銷。
關於打包驗證器的工作,改進來自於它需要執行的哈希操作數量的減少。這是因為打包的驗證者需要檢查更少的 Merkle 解除承諾證明。更具體地說,對於涉及見證函數和商函數 q(X) 的 Merkle 樹,打包驗證器會散列更大的葉子來檢查 Merkle 成員資格證明,但數量較少。此外,打包驗證器檢查與 FRI 的單次執行相對應的 Merkle 取消路徑。
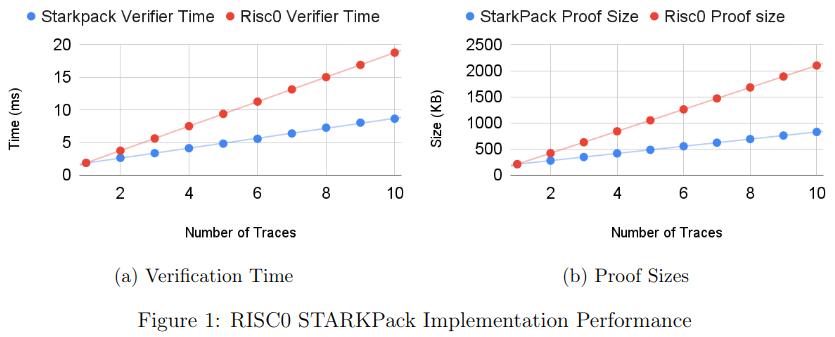
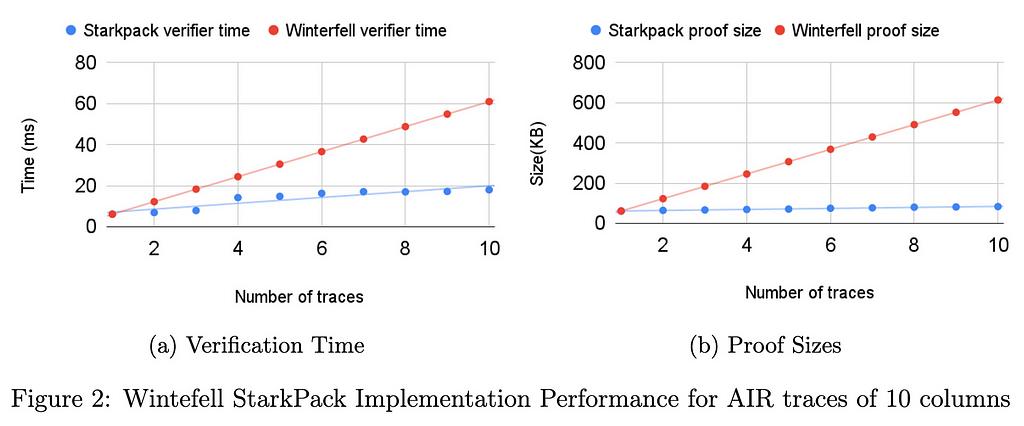
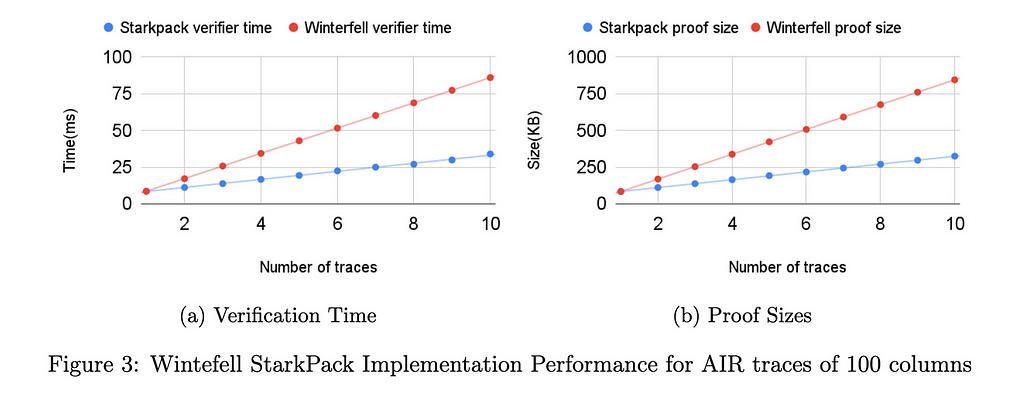
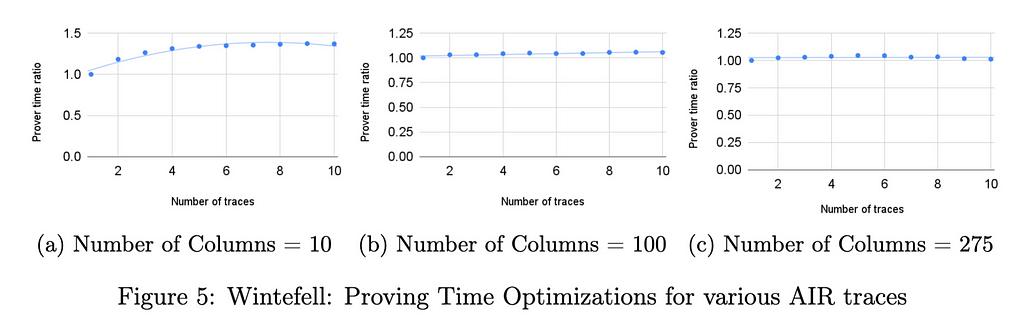
我們的初始基準(參見性能部分)表明,對於大小為 21⁶×100 的痕跡,與使用 Winterfell 順序證明所有實例的可滿足性相比,驗證者時間和證明大小都減少了一半以上。在 RISC0 中,即使跡線具有固定數量的列 (275),驗證器時間和證明大小的兩倍改進仍然適用。當然,使用打包技術時要付出的代價是,隨著批處理函數數量的增加,協議的可靠性會受到損失。在我們即將發佈的技術文件中,我們正式證明了結構的健全性。
我們注意到,對於涉及見證函數和商函數 q(X) 的 Merkle 樹,樹第一層的 Merkle 解除承諾的成本不會通過我們的打包技術進行攤銷。這是因為,如前所述,Merkle 樹葉現在是評估向量(每個打包實例一個),因此,它們的大小隨著打包實例的數量 N 線性增長。這部分解釋了為什麼在我們的實驗中,打包驗證器的工作量主要與跡線數量 N 呈線性關係。
我們還認為該技術應該減少證明者時間,原因與減少驗證者時間的原因類似。然而,隨著列和打包實例數量的增長,計算組合 DEEP-ALI 約束所需的現場操作成本變得越來越重要。事實上,在我們的技術中,組合約束函數的計算沒有攤銷。隨著我們批量處理的 RAP(或 AIR)實例中的列數增加,此成本占主導地位。我們在下面所示的基準測試中看到了這一點,對於大量列 (275),證明時間的改進約為 5%。
應用領域
我們在下面討論一些封裝技術的示例應用。如前所述,值得注意的是,我們可以為來自不同算術化的實例(例如 AIR 實例和 TurboPlonk(或 Plonk-ish)實例)的同時可滿足性生成單一證明。這可能很有趣,具體取決於每個算術化提供的權衡以及不同的彙總使用具有不同算術化的證明系統的事實。此外,打包技術可以很容易地適應於打包不同校樣系統的校樣。
以下所有三個應用程序都依賴於相同的原理。即,在STARK遞歸證明之間使用打包方法來減小驗證器電路和遞歸見證人的尺寸。因此,這會導致更快的遞歸證明器。在我們即將發表的技術論文中,我們將提供該策略帶來的改進的基準。這些應該至少與我們在下一節中提供的簡單初始基準一樣有益。
Zk-Rollups: STARK 被著名的區塊鏈公司廣泛使用,構建稱為 zk-rollups 的基於零知識證明的以太坊擴展解決方案。其中包括 StarkWare、 Polygon和 zkSync。最近,zkSync推出了基於Stark的L2解決方案,稱為Boojum, Polygon部署了Polygon Miden,Starkware部署了Starknet;全部遵循相似的架構。從Polygon L2平臺描述[Tea22]可以看出,在Layer 2上,每筆交易的正確性都通過獨立的STARK證明來證明,並且所有交易的STARK證明都是獨立但並行生成的。隨後,這些獨立的 STARK 證明通過遞歸證明組合來合併。生成的批量證明是遞歸 STARK 證明,確保所有輸入證明的有效性。
我們的技術可以通過首先使用打包生成大量獨立交易有效性的聚合證明來優化此工作流程,從而生成更小且更便宜的驗證證明。因此,下一次遞歸迭代對於證明者來說更便宜,因為驗證者電路和見證者都更小。這也可以在進一步的遞歸層中重複。
批量證明者: Starknet 推出了 SHARP,這是一個共享證明者系統,旨在鏈下處理批量的 Cairo 計算程序,其證明通過 Solidity 驗證者合約在鏈上進行驗證。由於STARK程序驗證成本是多對數的,不同用戶提交的各種Cairo程序可以在一個證明中批量驗證,有效地將驗證成本分配給所有程序。 SHARP 的最新版本採用了遞歸證明,每個程序在到達時最初都會單獨進行驗證。然後,這些單獨的證明逐漸合併成遞歸證明。這個過程一直持續到最終證明準備好提交給鏈上驗證者合約為止。我們提出的方法旨在提高 SHARP 遞歸證明的效率。我們的打包參數允許同時捆綁和證明多個語句,而不是單獨證明每個程序(該過程後來成為遞歸證明者輸入的一部分),從而產生更緊湊且更快驗證的證明。這可以降低與生成遞歸證明相關的成本。
以太坊單槽最終性:以太坊基金會最近提出了構建單槽最終性共識系統的基本想法 [KKZM23]。該說明討論了兩種概念上不同的基於樹和基於八卦的簽名聚合拓撲,這兩種拓撲都依賴於高效的簽名聚合技術。聚合方案允許將多個簽名合併為一個,並且還跟蹤所有參與簽名者的身份。此用例的困難在於每個參與者可以多次出現在聚合過程中。雖然有一些眾所周知的簽名方案可以實現高效聚合,例如 BLS,但當每個簽名者可以在聚合過程中多次出現時,跟蹤所有簽名者仍然是通信複雜性方面的一個挑戰。該說明討論了一個名為“簽名合併”的新概念,旨在通過零知識密碼學有效解決此問題。用於實例化簽名合併方案的建議方法之一是基於遞歸 STARK。遞歸 STARK 的特殊之處在於,計算包含其他 STARK 證明的驗證,這反過來又驗證與所提供的位字段相關的聚合簽名的正確性。由此產生的遞歸 STARK 證明可確保傳入的證明有效,並且其位域的並集等於所聲稱的結果。正如 [KKZM23] 中所解釋的,用於簽名合併的遞歸 STARK 的限制因素之一是證明的大小。這正是我們可以在遞歸生成最終證明之前首先利用打包證明聚合技術而不是獨立的 STARK 證明的場景。同樣,我們可以在每一層遞歸中應用相同的想法,並且這種方法總體上計算成本更低。
基準測試
我們已經在 Winterfell 和 RISC0 STARK 庫中實現了打包技術。 Winterfell 允許寫入任意跡線,並在優化跡線方面提供出色的靈活性。 RISC0 架構修復了 AIR 的某些結構元素,以便所有跟蹤都具有獨立於程序的固定數量 (275) 列。列數對最終批量證明和驗證性能起著重要作用。
我們在兩個庫中運行了不同的基準測試。在所有基準測試中,行數固定為 21⁶。在臨冬城,電路的列數從 10 到 275 不等,在每列計算從 i=1 到 i=21⁶ 的轉換 x_{i+1} = x_i3 + 42。在 RISC0 中,對於證明知道數字的兩個素因數的電路,跡線固定為 275 列。所有測試均在具有 32GB RAM 的 Intel i712700F 機器上運行。對於基準測試實例,證明時間的加速約為 5%。證明時間的優化可以忽略不計,這是由於列數較多。下面描述的針對具有較少列的跡線的 Winterfell 基準顯示了證明時間優化如何取決於列數。
下圖顯示了在 RISC0 中針對 275 列的 AIR 跟蹤以及在 Winterfell 中針對 10、100 和 275 列的跟蹤實現的 StarkPack 性能改進。
結論
這篇文章旨在提供基於 FRI 的 SNARK 聚合方法的高級總結,強調我們最初的基準測試所證明的驗證複雜性和證明大小方面的改進。技術論文中將對該技術和進一步的技術進行全面的解釋,並進行合理性分析。
參考
[BGK+23] Alexander R. Block、Albert Garreta、Jonathan Katz、Justin Thaler、Pratyush Ranjan Tiwari 和 Michał Zając。週五的 Fiat-shamir 安全及相關問題。密碼學 ePrint 檔案,論文 2023/1071,2023, https://eprint.iacr.org/2023/1071。
[BSCI+20] Eli Ben-Sasson、Dan Carmon、Yuval Ishai、Swastik Kopparty 和 Shubhangi Saraf。裡德-所羅門碼的鄰近間隙。密碼學 ePrint 檔案,論文 2020/654,2020。https ://eprint.iacr.org/2020/654。
[KKZM23] 喬治·卡迪亞納基斯、德米特里·霍夫拉托維奇、張振飛和瑪麗·馬勒。大規模共識的簽名合併,2023 年。https://ethresear.ch/t/signature-merging-for-large-scale-consensus/17386。
[KST21] Abhiram Kothapalli、Srinath Setty 和 Ioanna Tzialla。 Nova:來自摺疊方案的遞歸零知識論證。密碼學 ePrintArchive,論文 2021/370,2021。https ://eprint.iacr.org/2021/370。
[MAGABMMT23] Héctor Masip-Ardevol、Marc Guzmán-Albiol、Jordi Baylina-Melé 和 Jose Luis Muñoz-Tapia。 estark:用參數擴展斯塔克斯。密碼學 ePrint 檔案,論文 2023/474,2023。https ://eprint.iacr。 org/2023/474。
[Sta21] 斯塔克韋爾。 ethSTARK 文檔。密碼學 ePrint 檔案,論文 2021/582,2021。https ://eprint.iacr.org/2021/582。
[Tea22] PolygonZero 團隊。Polygon米登,2022。https :// Polygon。技術/多邊形米登。
關於 Nethermind 研究
Nethermind Research融合了密碼學、去中心化金融 (DeFi) 和協議研究領域,創造了增強各個領域的協同效應。
在這裡閱讀更多內容:
https://www.nethermind.io/applied-cryptography

STARKPack:聚合 STARK 以實現更短的證明和更快的驗證,最初發佈於Nethermind。 ETH在 Medium 上,人們通過強調和回應這個故事來繼續對話。