探索 ZK-SNARK – 第 1 部分：“zk-SNARK 背後的數學和編碼知識”

前言

在區塊鏈背景下， zk-SNARK是一種先進的安全技術，可以增強隱私並確保加密交易的透明度。

Zk-SNARK允許在不洩露知識的情況下證明知識，從而絕對保護用戶信息。

Zcash是領先的加密貨幣，採用zk-SNARK技術使交易完全匿名化，保證高安全性，不洩露用戶個人信息。這提高了用戶進行在線交易時的安全性和可靠性。

在“探索 ZK-SNARKs”研究系列的第 1 部分中，我將深入研究有關 zk-SNARKs 的重要細節以及該技術背後的基本算法和加密，以便您輕鬆理解。

zk-SNARK的概念和作用機制

zk-SNARK 基礎知識

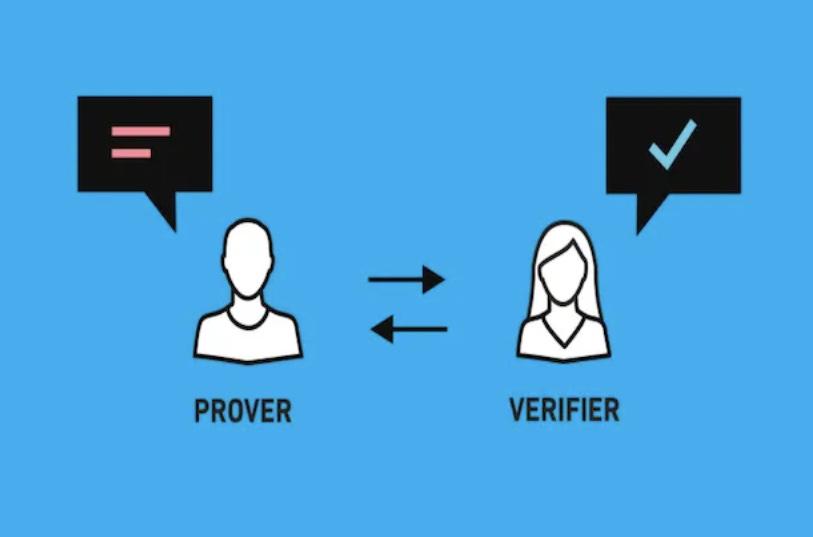
Zk-SNARK的全稱是Zero-Knowledge Succinct Non-Interactive Argument of Knowledge ，大致譯為“非知識披露的簡潔非交互式證明”（我這樣翻譯是為了更容易理解）。這是一種證明結構，允許一方（證明者）證明他們擁有某些信息，例如密鑰，而無需透露該信息，也不需要與另一方（驗證者）合作。

目前，zk-SNARK 是最流行的證明系統。

我們將把首字母縮略詞“zk-SNARK”分成更小的部分，以最清晰的方式檢查它們的含義。

• “零知識” ：這意味著輸入信息將被隱藏，不會透露給驗證者。換句話說，驗證者無法知道有關該知識的任何信息，只能知道其有效性。
• “簡潔”（短） ：這意味著生成的證明尺寸很小，大約幾百字節，並且驗證很快。這是SNARK帶來的第一個好處。
• “非交互” ：這是 SNARK 的第二個好處，雙方（證明者和驗證者），證明由從證明者到驗證者的單個消息組成，無需來回通信。
• “知識論證” ：是一個技術術語，意思是如果驗證者接受證明，那麼證明者必須實際上知道與被證明的聲明相關的秘密（而不僅僅是讓驗證者相信該陳述是真實的）。

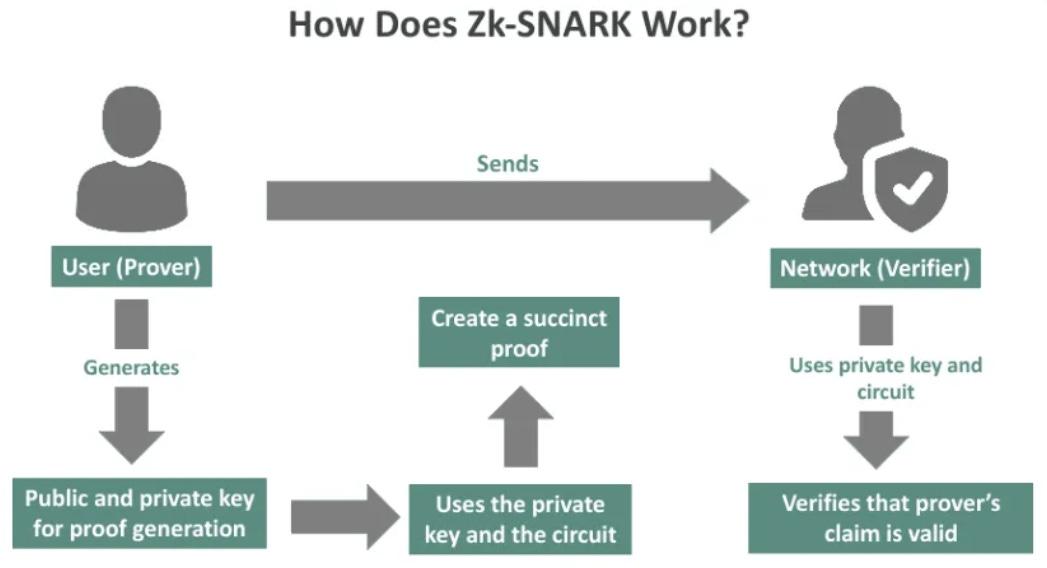
作用機制

從數學上來說， zk-SNARK包括 3 種算法：

• 密鑰生成（KG） ：這是一種密鑰生成算法，它將生成一對密鑰，一個用於證明（ pk ），一個用於驗證（ vk ）。密鑰生成算法以安全參數λ和程序C作為輸入，然後輸出密鑰。此步驟也稱為可信設置步驟。我們將在下面的部分詳細介紹它。 (pk, vk) = KG(λ, C)
• 證明（P）：該證明算法將通過輸入證明密鑰pk 、陳述x和見證人w來進行證明。輸出是一個prf證明。 prf = P(pk, x, w)
• 驗證（V） ：驗證算法將驗證密鑰vk 、語句x和證明prf作為輸入。輸出是接受或拒絕。

驗證結果 = V(vk, x, prf)

ZK-SNARK 的優點

• ZK-SNARK 帶來了許多重要的好處，特別是在增強各種應用程序的匿名性、安全性、可擴展性和交易效率方面。以下是軟件應用程序的 2 個主要優勢：
  1. 隱私：“零知識”屬性允許隱藏與計算相關的敏感數據，同時仍然證明語句的正確性。換句話說，zk-snark 在不洩露個人信息的情況下進行交易，保持交易信息的匿名性和安全性。這在 Zcash 等加密貨幣中非常有用，用戶可以在不透露交易金額、來源或目的地的情況下發送資金。
  2. 可擴展性：由於證明大小小和驗證時間短，驗證者可以快速知道計算是否忠實執行，而無需重新運行計算，從而減少驗證複雜計算所需的時間和資源，從而提高系統性能和可靠性，同時還有助於降低成本並增強其可擴展性。

值得信賴的設立儀式

信任建立過程是一個重要步驟，只需執行一次即可生成一組必要的數據，以便以後每次部署加密協議時使用。

在 ZK-SNARK 中，此信任設置步驟對於生成證明和驗證密鑰是必要的。然後將這些密鑰公開，允許參與者使用它們來創建和驗證證據。

對於每個新的 C 程序，需要執行新的可信設置，因為它取決於該 C 程序的詳細信息。在設置過程中，KG 密鑰生成過程使用秘密 lambda 和 C 程序作為輸入來生成公鑰 (pk) 和驗證密鑰 (vk)。

(pk, vk) = KG(λ, C)

因此，可靠的設置過程不是標準的，應該針對每個新程序單獨進行。

有毒廢物（有毒廢物）

可靠的設置需要一個名為lamda的秘密參數。這個參數通常被稱為“有毒廢物”，有時會導致 zk-SNARK 難以應用於實際應用。

這是因為，誰掌握了這個參數，就有能力製造假證據。具體來說，lambda 持有者可以為任何具有公共輸入 x 的 C 程序生成一個名為fakeProof的假證明，這樣

V(vk,x,fakeProof)=true

在不知道秘密證人w 的情況下被評估為真實。這是災難性的！

為zk-SNARK生成公共參數的最有效方法是通過某人生成公鑰和私鑰對（類似於ECDSA密鑰對），然後銷燬私鑰。但令人擔憂的是，如何確定這邊確實已經消除了那些“有毒廢物”呢？

因此，為了解決這個問題，應用了多方計算（MPC） 。

MPC是一種密碼協議，允許多方以分佈式方式參與計算，而任何一方都無法訪問另一方的機密數據。

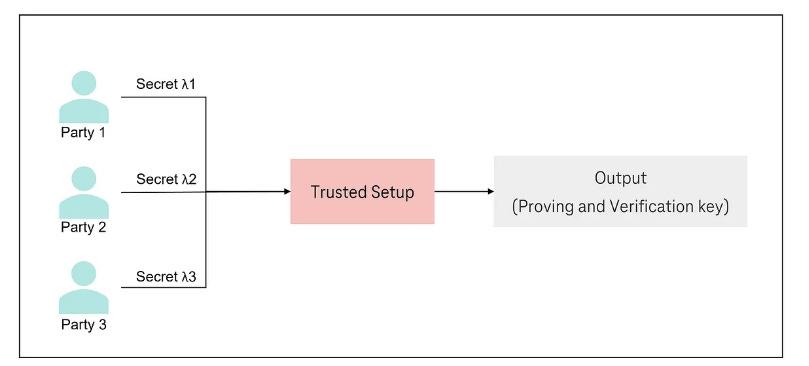
在每個信任建立過程中，多方共同參與生成必要的密碼組件，例如公鑰（pk）和驗證密鑰（vk） 。各方都為此過程貢獻了部分機密數據。

此過程後各方的最終目標是徹底消除有毒廢物。這種情況下的可靠性假設是，只要 n 個參與者之一是誠實的，最終結果就保證是安全的。

在信任設置期間， n方中的每一方都會攜帶其秘密lambda來共同生成證明和驗證密鑰。

要使此設置失敗，需要所有 n 方都懷有惡意並互相分享他們的秘密。然而，只要其中一方決定不洩露其秘密，信託的建立過程仍然會成功，從而不可能產生虛假證據。

zk-snark 背後的數學和編碼

數學基礎

群論

ZK-SNARK 利用群論對橢圓曲線和其他群進行計算，特別是在使用雙線性配對和相關算法時。

簡單來說，群就是一組元素{a,b,c,…}的二元運算組合，這裡用“•”表示。

如果集合和運算滿足以下屬性，則稱為群：

• 閉包：對於G組中的所有a和b，操作a·b也必須屬於G。
• 結合性：對於G中的所有a、b和c，運算(a•b)•c必須等於a•(b•c)。
• 單位元素： G 中必須存在一個元素 e，使得對於 G 中的每個元素 a，操作 e•a 和 a•e 等於 a。這個元素是獨一無二的。
• 逆元素：對於G中的每個元素a，G中必須有一個元素b，通常稱為a^-1，使得操作a•b和b•a等於來自單元e的操作。

亞組

當群中元素的子集服從該群的所有屬性時，該集合稱為原群的子群。

領域

域是一種特殊的代數結構，其中一組元素執行兩個基本運算：加法和乘法。每個領域都必須遵守一系列基本公理，這些公理定義並保證了其一般屬性。

以下是域必須滿足的公理，其中 a、b 和 c 是域 F 的任何元素：

1. 計算加法和乘法的組合：a + (b + c)= (a + b) + c anda · (b · c) = (a · b) · c
2. 加法和乘法的交換律：a + b = b + a 和 a·b = b·a
3. 加法和乘法相等：F 中存在兩個不同的元素 0 和 1，使得 a + 0 = a 和 a·1 = a
4. 加法逆元：對於 F 中的每個 a，F 中都存在一個元素，表示為 -a，稱為 a 的加法逆元，使得 a + (−a) = 0
5. 乘法逆元：對於 F 中的每個 a≠ 0，F 中都存在一個元素，記為 a^ -1，稱為 a 的乘法逆元，使得 a · a^ -1 = 1
6. 乘法相對於加法的分佈：a· (b + c) = (a·b) + (a·c)

字段的示例包括具有加法和乘法的實數集，以及以素數為模的整數，其中定義了加法和乘法。

有限域

在ZK-SNARK中，所有運算都在有限域中執行，其中值和運算以素數為模或基於素數多項式定義。

有限域是具有有限數量元素的域，例如以 p 為模的整數集，其中 p 是素數。

對於有限域，域中元素的數量（稱為域的階）可以是：

• 一些素數（素數域）
• 或者素數的冪（擴展域）

在簡單素數域中，元素可以用0到p-1 之間的整數表示，其中Zp = {0, 1, …, p-1}。

Zp的擴展稱為乘法群Zp* ，由與p互質的元素組成，即Zp* = {1, …, p-1}。

有限域生成器

在每個有限域中，總是存在一個稱為生成器的元素，它能夠使用其求冪生成群中的所有元素。

例如，考慮素數域中的群Z5* Z5 = {0, 1, 2, 3, 4} ，則Z5* = {1, 2, 3, 4} 。在群Z5*中，乘法是二元運算，並且乘法以模 5 執行；例如，3 × 4 相乘不會得到 12，而是 2，因為 12 mod 5 = 2。

群Z5*是循環群並具有生成元 2 和 3，因為：

• 對於生成器 2，我們有：

2^0 = 1,

2^1 = 2,

2^2 = 4,

2^3 = 3,

2^4 = 1（重複循環）

• 對於生成器 3，我們有：

3^0 = 1,

3^1 = 3,

3^2 = 4,

3^3 = 2,

3^4 = 1（重複循環）

這些屬性使Z5*成為密碼運算的強大組，並且常用於ZK-SNARKs等密碼算法中。

群同態

同態是兩個相似的代數結構（例如群或域）之間的映射，並且它們保留該結構內的運算。

具體來說，同態是從A組到B組的映射f ，當這兩個組具有相同的二元運算（例如乘法或加法）時。此映射保留了操作，這意味著：

如果 ⋅ 是A組和B 組結構中的二元運算，則對於A組中的所有元素a和b ，映射f滿足條件：

f ( x ⋅ y )= f ( x )⋅ f ( y )

這確保了應用於組A中的元素的操作結果在通過f映射到組B後，仍然等於直接對組B執行的操作。

同態是處理雙線性對屬性的基礎，使得zk-SNARK中生成和驗證證明的過程更加高效。

多項式

多項式是構建二次算術程序 (QAP)的核心組成部分，其中問題通過多項式表示並通過多項式評估和承諾來解決。

多項式是由變量和常數組成的數學表達式，使用加法、乘法和非負整數指數求冪。

例如，多項式5x² + 2x + 8就是一個典型的例子。

當考慮多項式方程時，它可以表示數字之間無數個不同的方程。例如，如果方程A(x) + B(x) = C(x)成立，那麼對於 x 的所有值也成立，例如：

A(0) + B(0) = C(0)

A(1) + B(1) = C(1)

A(2) + B(2) = C(2)

A(3) + B(3) = C(3)

等等。

關於多項式的次數，由多項式中變量的最大冪決定。例如，多項式 6x⁴ + 2x³ + 3 的次數為 4，因為變量 x 的最高次方為 4。

密碼學

哈希函數

哈希函數廣泛用於在加密協議中創建“承諾” ，有助於確保數據無法在未經檢測的情況下被修改。

哈希函數是一種算法或數學函數，它將可變長度的輸入數據字符串轉換為固定長度的輸出字符串（稱為哈希值）。

哈希函數表示公式可以描述如下：

f(米)=H

其中f是哈希函數， m是消息， H是結果哈希值。

哈希函數具有許多重要的屬性，使其在許多密碼應用程序中非常有用。這些屬性包括：

• 原像抵抗：從數學上講，從哈希值中檢索原始消息非常困難。
• 第二原像抵抗：給定特定的輸入消息及其哈希值，很難找到產生相同哈希值的另一條消息。
• 抗碰撞性：很難找到產生相同哈希值的兩個不同消息。

好的哈希函數的一個非常理想的特性是雪崩效應。 這是輸入的微小變化會導致輸出發生較大變化的特性，使輸出顯得隨機且難以區分。

加密

簡而言之，加密是將輸入消息（明文）轉換為看似隨機的輸出（密文）的過程，以便只有授權的人才能解碼和理解該信息。加密基於密鑰的使用，密鑰是發送者和接收者用來加密和解密信息的一組數學值。

加密算法有兩種類型：對稱加密和非對稱加密。

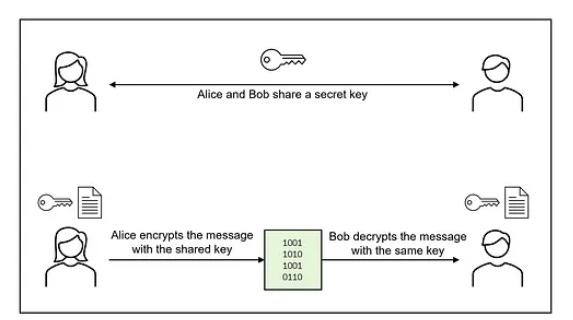
對稱加密

在對稱加密中，通信過程中涉及的各方使用相同的密鑰來加密和解密消息。該密鑰在雙方之間保密，以確保交換信息的安全。

非對稱加密

在非對稱加密中，也稱為公鑰加密，有兩種類型的密鑰：用於加密的公鑰和用於解密的私鑰。私鑰由接收者保密（因此稱為“私鑰”），而公鑰可以與任何想要發送機密信息的人廣泛共享（因此稱為“私鑰”）。

非對稱加密廣泛應用於以下幾種情況：

• 發送安全消息：發送者使用接收者的公鑰對消息進行加密，然後將其發送給接收者。只有擁有私鑰的接收者才能解密並讀取消息。
• 證明私鑰的所有權（知道）：在證明私鑰所有權的過程中，發送者用自己的私鑰對消息進行加密（或簽名），然後將其發送給接收者。接收者使用發送者的公鑰來解密消息。此過程通常稱為數字簽名，如此加密的消息稱為“數字簽名”。由此，數字簽名證明該消息是由擁有相應私鑰的人發送的，並且還有助於驗證消息中信息的完整性。

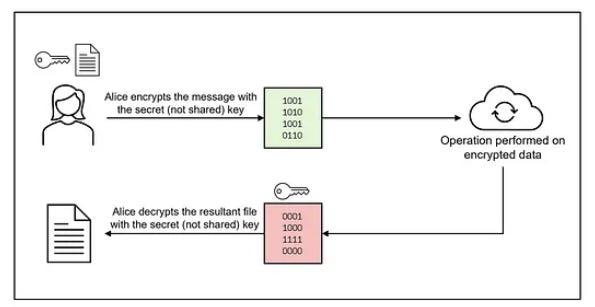
同態加密（Homomorphic crypto）

同態加密在高級零知識證明的設計中具有很大的影響力，因為它允許對加密數據進行計算而無需解密。

同態加密是一種特殊類型的加密，允許直接對加密數據執行計算。這意味著可以對加密數據執行額外的計算，而無需密鑰。這些計算的結果保持加密狀態，確保安全性，而不會洩露原始數據內容。

在實踐中，允許對加密數據進行各種任意計算的全同態加密仍然存在很多侷限性，尚未得到廣泛應用。然而，對同態結構進行某些操作是可行的，並且已經在實際應用中得到應用。

這些操作包括加密數據的加法和乘法，這為無需解密的安全數據處理開闢了新的可能性。

橢圓曲線密碼學 (ECC)

在 ZK-SNARK 中，由於執行雙線性配對的群運算，橢圓曲線發揮著重要作用。 ECC（橢圓曲線密碼學）為創建和驗證零知識證明提供了一個高效的平臺。

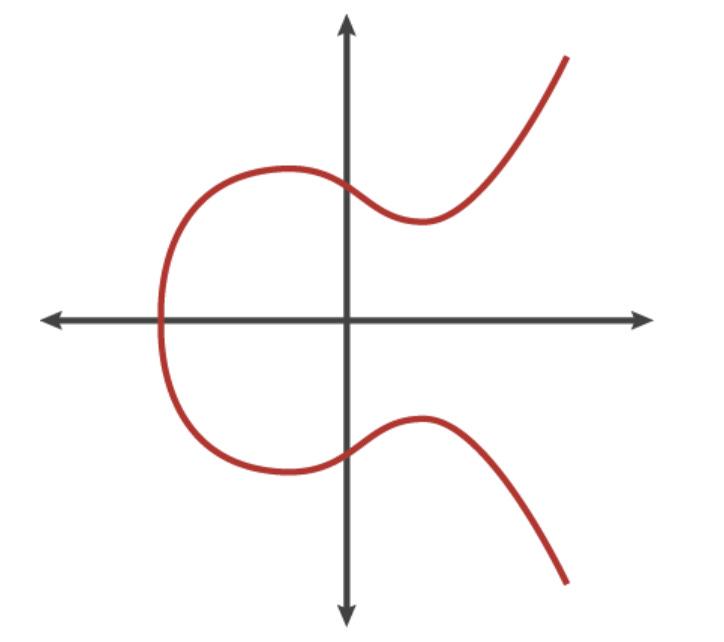
橢圓曲線是滿足特定數學方程的一組點。橢圓曲線的方程具有以下形式：

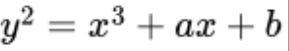
其中， a 、 b為已知常數。該方程的圖形如下所示：

橢圓曲線有許多不同的表示形式，但該技術主要是尋找滿足特定數學方程的點。

橢圓曲線的特性使其在許多數學領域，尤其是密碼學領域非常重要。

橢圓曲線的一個有趣的特性是它們的水平對稱性。曲線上的任何點都可以在x軸上進行反射，同時仍保持曲線不變。這意味著，如果您在曲線上取任意兩點並通過它們畫一條線，該線將在第三個點處與曲線相交。

想象一下這是一場檯球遊戲，球從一個點射出，當它擊中橢圓曲線時，它會垂直向上或垂直向下彈起，具體取決於它相對於x軸的位置。

橢圓曲線的一個有趣的特性是，您可以在曲線上“點”兩個點來創建一個新點。您還可以重複“點”一個點，以在曲線上創建不同的點。

但有趣的是，如果你知道終點和起點，計算從起點到終點所需的“點”數量是非常困難的！

想象一下一個人在一個房間裡獨自玩耍，按照遊戲規則擊球。然後其他人進來看看球的最終位置。即使他們知道初始位置和比賽規則，如果不從頭開始回顧整個比賽，他們也無法知道球被擊中了多少次。這在密碼學中創造了一個特殊的屬性，稱為不可逆性，並且是許多強大應用程序（例如陷門函數）的基礎。

橢圓曲線上的離散對數是一個難題，它是基於橢圓曲線的密碼學的基礎。與分解不同的是，沒有捷徑可以解決這個問題，這使得破解橢圓曲線加密比使用RSA和Diffie-Hellman更加困難。

雖然 ECC 通過較短的密鑰提供了高級別的安全性，但它在低功耗設備上仍然保留了良好的性能。這使得 ECC 成為資源有限的移動設備和系統上的加密應用程序的理想選擇。

在本節的最後，我闡述了zk-SNARK背後的一些基本數學和編碼概念，在下一節中，我將詳細闡述更高級的概念，例如二次算術程序、橢圓曲線配對。

感謝您閱讀本文。如果您喜歡這篇文章，別忘了關注並留下掌聲。

文章來源：團隊技術/研究 – AlphaTrue

參考來源：

1.資料來源：Reitwiessner, C. (2016)。簡而言之，zkSNARK。以太坊博客， 6，1-15 。 https://chriseth.github.io/notes/articles/zksnarks/zksnarks.pdf

2. https://medium.com/coinmonks/from-zero-to-hero-in-zero-knowledge-proofs-part-7-61d639c2ef02

3. https://celo.academy/t/zk-snarks-proofs-as-a-privacy-solution-on-the-blockchain/1961

4.資料來源：Chen, T.、Lu, H.、Kunpittaya, T. 和 Luo, A. (2022)。 zk-snarks 的評論。 arXiv 預印本 arXiv:2202.06877 。 https://arxiv.org/pdf/2202.06877.pdf

5. https://medium.com/coinmonks/from-zero-to-hero-in-zero-knowledge-proofs-part-8-262f923f1537

6. https://medium.com/@hira.siddiqui/from-zero-to-hero-in-zero-knowledge-proofs-part-2-ef17ce470f2d

7. 伊斯特姆，W.（2022）。 現代密碼學：加密和信息安全的應用數學。施普林格自然。

8. https://blog.cloudflare.com/a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/