前言
您準備好探索zk-SNARK更復雜的一面了嗎?在上一節中,我們學習了一些更高級的概念,例如算術電路和二次算術程序。在本節中,我們將通過深入研究另一個強大的概念來擴展我們的知識:橢圓曲線配對。
注意:深入理解橢圓曲線配對等主題有時對許多人來說是一個挑戰。然而,這就是我們寫這篇文章的原因——幫助您至少對此有一個基本的瞭解。
我的目標不僅是徹底解釋橢圓曲線配對,而且使該主題更有趣且易於理解。希望通過本文,您將看到橢圓曲線對在數學和密碼學中的強大功能,以及它們在zk-SNARK中的具體應用。
橢圓曲線
橢圓曲線是橢圓曲線密碼學領域的一部分。這是一個複雜的課題,不是每個人都能輕易理解的。為了更好地理解它們,請查看我上一節中關於 ECC 的文章。
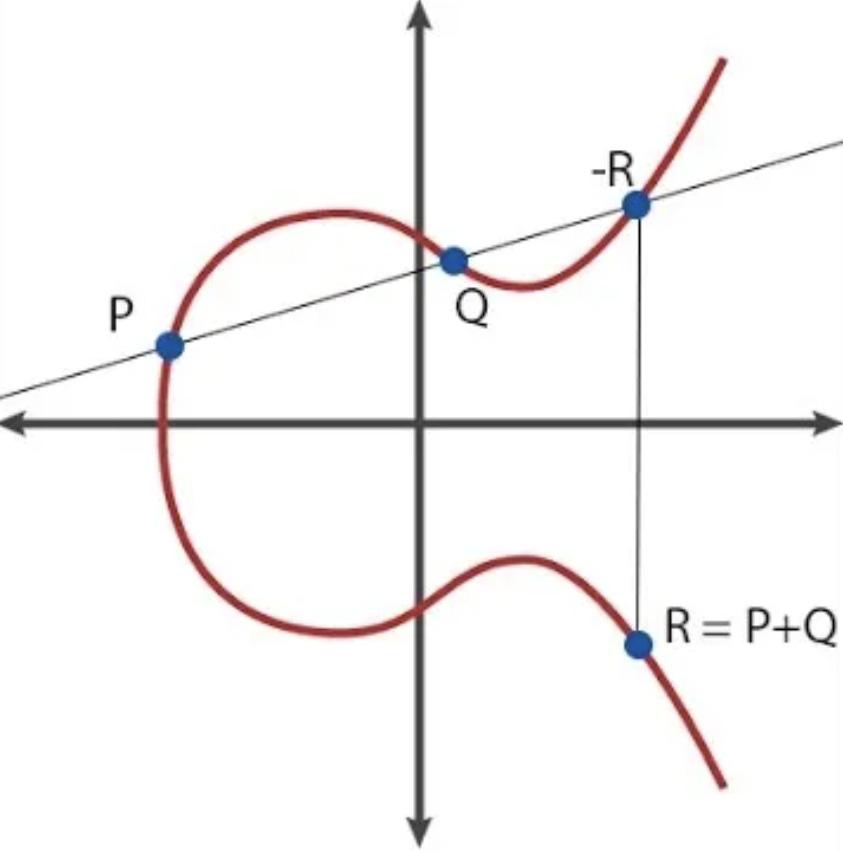
橢圓曲線密碼學涉及二維空間中的“點” ,每個“點”由一對(x, y)座標來表徵。
執行點之間的加法和減法等數學運算有特定的規則,允許在已知其他點的情況下計算新點的座標。
示例:計算座標R = P + Q
您還可以將點與整數相乘,方法是重複將點與自身相加,次與該整數相同。
例如: P * n = P + P + … + P
這提供了一種在橢圓曲線密碼學中執行數學運算的有效方法
在橢圓曲線上,有一個特殊的點,稱為“無窮遠點” ( O ),相當於點微積分中的數字 0, P + O = P始終成立。
曲線也有“階” ;對於所有P ( P * (n+1) = P、P * (7*n + 5) = P * 5等等),存在一個數字 n,使得P * n = O。
此外,還有一個“生成點”(G ),可以理解為以某種方式代表數字1。理論上,曲線上的任何點(除了O )都可以是G 。
配對
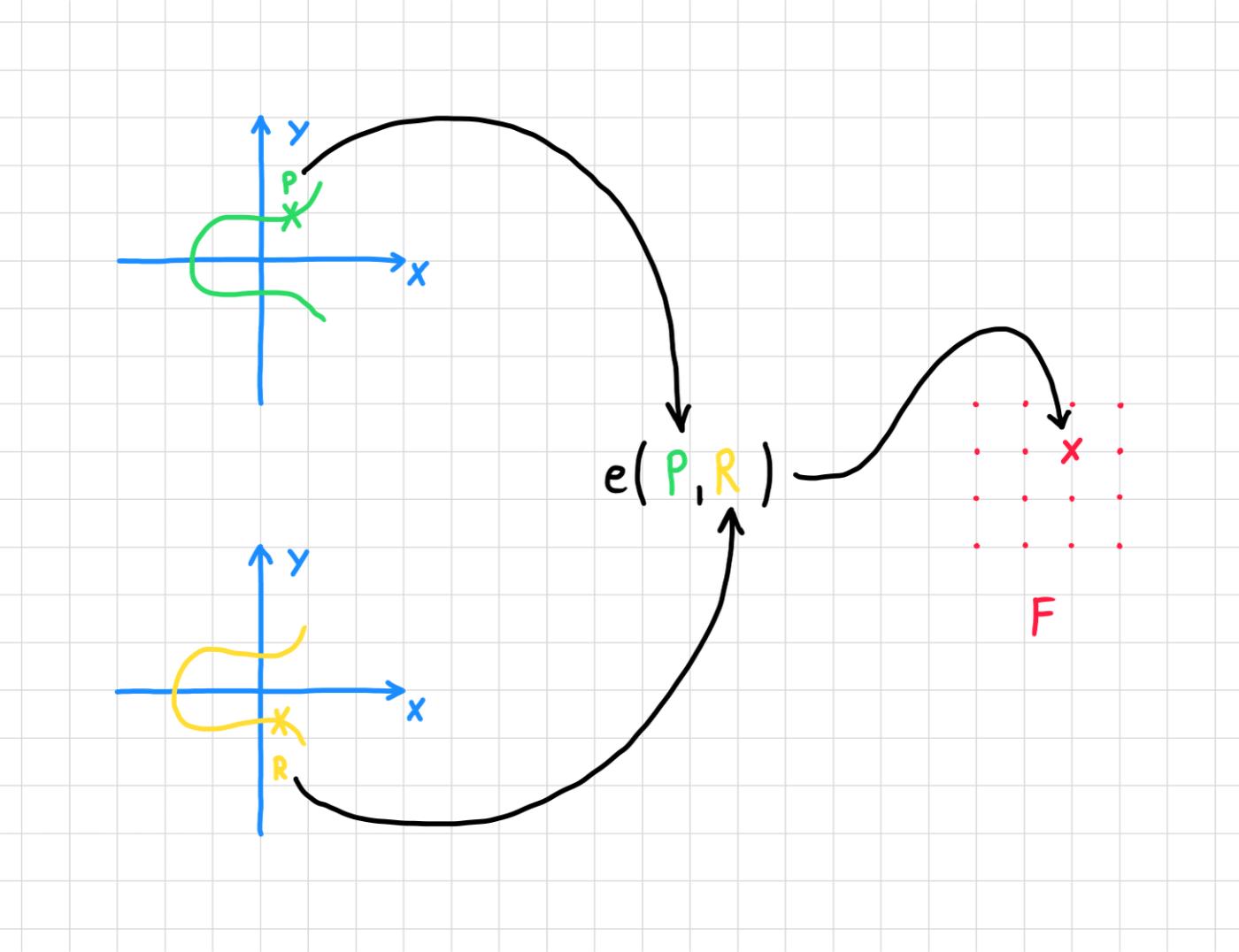
配對允許在橢圓曲線的點上測試更復雜的方程。
例如:
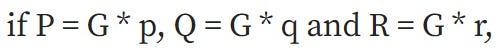
您可以僅根據P、Q和R檢查p * q是否等於r 。
儘管有關p的信息可能會從P洩漏,但這種洩漏是經過仔細控制的。
配對允許檢查二次約束。
例如:測試e(P, Q) * e(G, G * 5) = 1實際上是測試p * q + 5 = 0 。

是一種稱為配對的操作。數學家也稱其為雙線性映射。這裡的“雙線性”將遵守以下規則:

請注意,您可以以任何方式使用+和*運算符,只要它們符合以下規則:

和
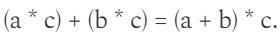
如果P、Q、R和S是簡單數字,則使用以下表達式可以輕鬆製作簡單的配對操作:
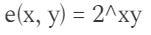
結果如下:
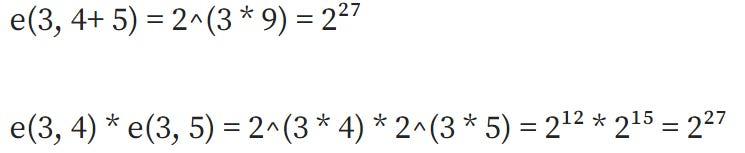
那就是平行線!
然而,這種簡單的配對操作並不適合密碼學,因為它們對簡單整數進行操作並且太容易分析。
當您在執行配對操作時知道一個數字及其結果時,您可以輕鬆計算並找到剩餘的數字。
我們使用像“黑匣子”這樣的數學運算,只能執行基本的數學運算,而無需進一步分析或理解。這就是為什麼橢圓曲線和橢圓曲線上的配對操作在密碼學中變得重要的原因。
素域和擴展域
可以在橢圓曲線點上製作雙線性映射- 即製作一個函數

其中P和Q是橢圓曲線點,結果是稱為F_p^2的元素類型
首先,讓我們瞭解素域和擴展域。
上圖中的橢圓曲線之所以如此美麗,是因為該曲線的方程是使用普通實數定義的。
然而,在密碼學中,使用傳統的實數可能會導致使用對數“倒退” ,並破壞事物,因為存儲和表示數字所需的空間量可以隨意上漲。因此,我們在素數域中使用數字。
素數字段包括數字0、1、2…p-1 的集合,其中p 是素數,各種運算定義如下:

所有運算均以p 為模
Chia是一種特殊情況;通常,3/2 不是整數,現在我只想處理整數,所以我嘗試找到數字x使得
x * 2 = 3 。
這可以使用擴展歐幾里得算法來完成。例如,如果p = 7 ,則:

接下來我們要講的是擴展字段。
您在數學書籍中經常遇到的一個常見示例是複數字段,其中實數字段通過附加元素sqrt(-1) = i進行“擴展”。
擴展字段的工作方式是採用現有字段,然後“添加”新元素並定義該新元素與原始字段中已有元素之間的關係(例如i² + 1 = 0 )。
重要的是這個方程對於原域中的任何數字都不成立,然後考慮原域中的元素和剛剛製作的新元素的所有線性組合。
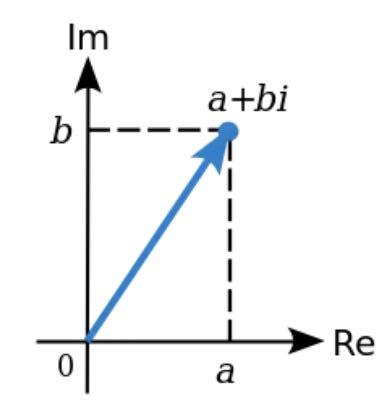
我們還可以擴展主要領域
例如,用 i擴展我們上面描述的素數域mod 7,我們可以執行以下操作:

如果您想查看代碼中完成的所有數學運算,則素數字段和字段擴展都可以在此處完成
橢圓曲線配對
橢圓曲線配對是一種從兩條橢圓曲線中獲取兩個點並將這些點映射為單個數字的機制。
您可以將此映射視為等效於橢圓曲線上的點相乘。
從數學上講,橢圓曲線配對定義為將橢圓曲線上的兩個點映射到另一個組(例如有限域)中的元素:
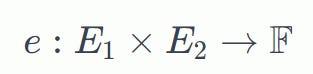
這裡e是配對, E 1 和E 2 是橢圓曲線,𝐹 是有限域。
請注意,橢圓曲線E 1 和E 2 不需要不同。
一旦發生串聯,結果是另一個組中的元素無法在下次串聯中重用。
橢圓曲線配對具有稱為雙線性映射的某些屬性:
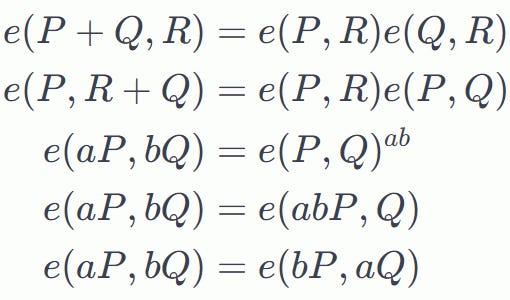
這裡P 、 Q和R是橢圓曲線上的點, 𝑎ε𝑍,𝑏ε𝑍
通過使用這些“雙線性映射” ,我們可以在這兩條曲線上“移動”係數𝑎和𝑏 ,同時保持映射不變:
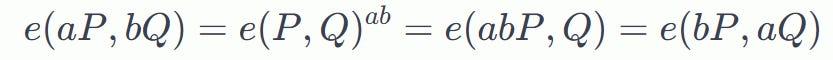
我們可以將橢圓曲線配對想象為G2 x G1 -> Gt的映射,其中:
G1是橢圓曲線,其中點滿足形式方程
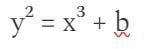
兩個座標都是F_p的元素(它們是簡單的數字,但運算是對特定素數取模)
G2也是一條橢圓曲線,其中的點滿足與G1相同的方程,但它們的座標屬於域F_p12 (我們定義一個新的“幻數” w ,由 12 次多項式定義,如下所示:

Gt是橢圓曲線的結果進入的對象類型。在我們考慮的曲線中, Gt是F_p^2 (與G2中使用的相同的強複數)
這裡它必須滿足雙線性:
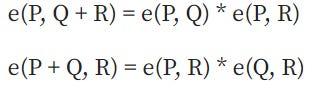
還有另外兩個重要標準:
- 高效的可計算性:高效的計算能力意味著能夠快速計算複合運算,並且不會太複雜。例如:如果我們簡單地取點的離散對數並將它們相乘以製作一個複合值,這在計算上會變得太困難,就像破壞原始的橢圓曲線頭一樣。因此,如果可以有效地計算複合運算而不施加太多的計算負擔,則該複合運算被認為是計算高效的。
- 非簡併性:非簡併性確保串聯不是無用的串聯,即它不只是返回獨立於輸入點的固定值。例如:如果我們將所有 P 和Q的耦合定義為e(P, Q) = 1 ,則這不會提供有關橢圓曲線上點之間關係的任何有用信息。因此,如果串聯提供了有關輸入點之間關係的有用信息,則該串聯被認為是非退化的。
那麼如何做到這一點呢?
首先,我們需要了解除數的概念,這是表示橢圓曲線上的點上的函數的另一種方式。
函數的除數本質上是計算函數的零數和無窮數。為了理解這意味著什麼,讓我們看一些例子。讓我們修復一些點P = (P_x, P_y) ,並考慮以下函數:
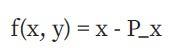
除數為[P] + [-P] – 2 * [O]
[P] + [Q]與[P + Q] 不同。原因如下:
- 該函數在P處為0,因為當x為P_x 時,因此x – P_x = 0。
- 該函數在-P處為0 ,因為-P和P具有相同的x座標。
- 當x趨於無窮大時,函數趨於無窮大,所以我們說函數在O處是無窮大的。
原因在於橢圓曲線的方程:
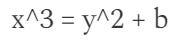
y上漲無窮大的速度大約比x快“1.5次”,以跟上x^3 的速度。因此,如果線性函數只有x ,則它將表示為 2 的倍數的無窮大,但如果函數有y ,則它將表示為 3 的倍數的無窮大。
現在,考慮一個“線函數” :
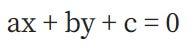
其中a、b和c經過精心選擇,使得直線穿過橢圓曲線上的點P和Q。
由於橢圓曲線上的加法的工作方式,這也意味著它通過點-PQ 。該函數也會根據x和y趨於無窮大,從而Chia成為的可能性
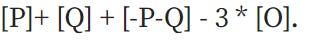

每個“有理函數” (在點座標上僅使用有限數量的+、-、*、/運算定義的函數)唯一對應於一個divsor ,其條件是乘以一個常數(即,如果兩個函數F和G有相同的除數,則F = G * k,其中k是常數)。
兩個函數的Chia等於每個函數的Chia之和,因此

然後
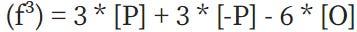
文章來源: Team Tech/Research Alphatrue
參考來源: