By: mutourend & lynndell, Bitlayer Labs

1 Introduction
For an algorithm f, two mutually distrusting parties, Alice and Bob, can establish trust in the following way:
Alice inputs x, runs algorithm f, and obtains result y. Bob also runs algorithm f based on the same input x, and the result is y′. If y = y′, then Bob recognizes the input x and output y provided by Alice. This is a special validity proof mechanism, which is often used in blockchain consensus. Among them, Alice is the node that packages the block, and Bob is the node that participates in the consensus.
Alice inputs x, runs the zk.prove program on algorithm f, and obtains the result y and proof. Bob runs the zk.verify program based on f, y, and proof. If the result is true, Bob recognizes Alice's result y; if the result is false, Bob does not recognize Alice's result y. This is a proof of validity. Among them, Bob can be an on-chain contract.
Alice inputs x, runs algorithm f, and obtains result y. Bob also runs algorithm f based on the same input x, and the result is y′. If y = y′, then do nothing; if y ≠ y′, then Bob challenges Alice, and the challenged program is f. Alice and Bob can interact once or multiple times. Arbitration is achieved according to the challenge response process. This is a fraud proof. Among them, Bob is the challenger, listening off-chain and challenging on-chain.
Alice inputs x and runs the zk.prove program on algorithm f to obtain the result y and proof. Bob runs the zk.verify program based on f, y and proof. If the result is true, nothing is done; if the result is false, Bob challenges Alice, and the challenged program is zk.verify. Alice and Bob can interact once or more. Alice and Bob can interact once or more. Arbitration is achieved according to the challenge response process. This is a fraud proof. Among them, Bob is the challenger, listening off-chain and challenging on-chain.
For 2, 3, and 4 above, let x be the Layer 2 transaction and the starting state, f be the Layer 2 consensus program, and y be the transaction end state, which corresponds to the blockchain Layer 2 expansion plan. Among them:
Validity Proof: Based on the pessimistic assumption, it must be proven to be valid before it is accepted, and it takes effect immediately. In the validity proof, it is necessary to provide evidence that the L2 state transition is correct, reflecting the pessimistic view of the world - a state will be accepted only if and only if it is proven to be correct.
Fraud Proof: Based on optimistic assumptions, it is accepted by default unless someone proves it is wrong. It has a challenge window period, and it will take effect only after the challenge window period. In a fraud proof, it is necessary to provide evidence that the L2 state transition is incorrect, reflecting an optimistic view of the world - a state transition is correct by default unless it is proven to be incorrect.
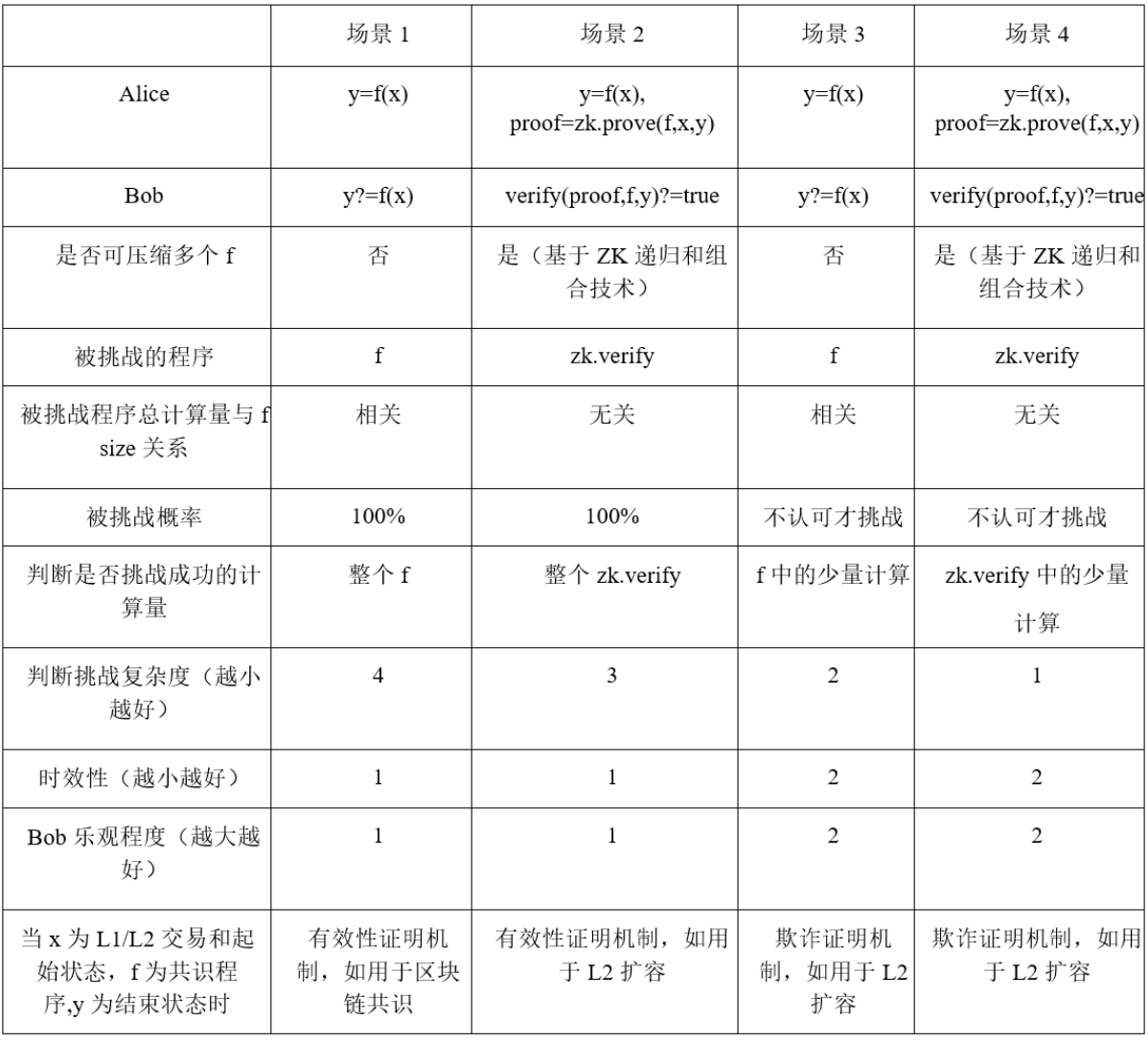
Table 1: Trust building methods
In addition, please note that:
The key to distinguishing fraud proofs from validity proofs is not whether a ZK proof system such as SNARK/STARK is used. The ZK proof system expresses the proof method used, while fraud or validity represents the content of the proof. This is why scenario 1 in Table 1 represents a validity proof.
The validity proof has better timeliness, but the on-chain verification complexity is relatively high; the fraud proof has lower on-chain verification complexity, but relatively poor timeliness.
For cases 2 and 4 in Table 1, with the help of ZK recursion and combination technology, multiple f can be calculated and compressed, greatly alleviating and reducing the verification cost of off-chain calculations on the chain.
Currently, benefiting from Solidity Turing-complete smart contracts, fraud proof and validity proof technologies are widely used in Ethereum Layer 2 expansion. However, under the Bitcoin paradigm, these technical applications are still in the exploratory stage due to Bitcoin's limited opcode functions, 1,000 stack elements and other limitations. This article summarizes the limitations and breakthrough technologies under the Bitcoin paradigm in the Bitcoin Layer 2 expansion scenario, studies validity proof and fraud proof technologies, and sorts out the script segmentation technology unique to the Bitcoin paradigm.
2 Limitations and Breakthroughs under the Bitcoin Paradigm
There are many limitations under the Bitcoin paradigm, but various clever methods or technologies can be used to break through these limitations. For example, Bit Commitment can break through the UTXO stateless limitation, taproot can break through the script space limitation, connector output can break through the UTXO spending method limitation, and contracts can break through the pre-signing limitation.
2.1 UTXO Model and Script Restrictions
Bitcoin uses the UTXO model, where each UTXO is locked in a locking script that defines the conditions that must be met to spend the UTXO. Bitcoin scripts have the following limitations:
Bitcoin Script is stateless;
For P2TR output types, the total number of opcodes that can be accommodated in a single transaction is up to about 4 million, which will fill the entire block, while for other output types it is only 10,000 opcodes;
The spending methods of a single UTXO are limited, and there is a lack of exploration of combined spending methods;
Does not support flexible contract functions;
The stack size is limited to 1000 elements (altstack + stack), and the maximum size of a single element is 520 bytes;
Arithmetic operations (such as addition and subtraction) are limited to 4-byte elements. They cannot be modified to longer elements, such as 20 bytes or larger, which is required for cryptographic operations;
Opcodes such as OP_MUL and OP_CAT have been disabled. If existing opcodes are used for simulation, the cost is extremely high. For example, to simulate a one-round BLAKE3 hash, the script size is about 75K.
2.2 Bit Commitment: Breaking through the UTXO stateless limitation
Currently Bitcoin scripts are completely stateless. When a Bitcoin script is executed, its execution environment is reset after each script. This results in Bitcoin scripts not being able to natively support constraining script 1 and script 2 to have the same value of x. However, there are ways to circumvent this problem, the core idea being to sign a value in some way. If a signature can be created for a value, then a stateful Bitcoin script can be implemented. That is, by checking the signature of the x value in script 1 and script 2, the same value of x can be enforced in script 1 and script 2. If there is a conflicting signature, that is, 2 different values are signed for the same variable x, it can be penalized. This solution is called bit commitment.
The principle of bit commitment is relatively simple. The so-called bit refers to setting two different hash values, hash0 and hash1, for each bit in the signature message. If the bit value to be signed is 0, the preimage preimage0 of hash0 is revealed; if the bit value to be signed is 1, the preimage preimage1 of hash1 is revealed.
Taking a single bit message m ∈ {0,1} as an example, the corresponding bit commitment unlocking script is just some preimages: if the bit value is 0, the corresponding unlocking script is preimage0 - "0xfa7fa5b1dea37d71a0b841967f6a3b119dbea140"; if the bit value is 1, the corresponding unlocking script is preimage1 - "0x47c31e611a3bd2f3a7a42207613046703fa27496". Therefore, with the help of bit commitment, the stateless limitation of UTXO can be broken and stateful Bitcoin scripts can be realized, making various interesting new features possible.
OP_HASH160
OP_DUP
<0xf592e757267b7f307324f1e78b34472f8b6f46f3> // This is hash1
OP_EQUAL
OP_DUP
OP_ROT
<0x100b9f19ebd537fdc371fa1367d7ccc802dc2524> // This is hash0
OP_EQUAL
OP_BOOLOR
OP_VERIFY
// Now the value of the bit commitment is on the stack. Either ”0” or ”1”.
There are currently two ways to implement Bit Commitment:
Lamport one-time signature: The principle is relatively simple and only requires the use of hash functions, so it is Bitcoin-friendly. For each bit in the message, 2 hash values need to be committed, resulting in a relatively large signature data. In other words, for a message of length v bits, the public key length is 2v bits and the signature length is v bits.
Winternitz one-time signature: Compared with Lamport signature, it can significantly reduce the length of signature and public key, but increase the complexity of signing and verification. This scheme can flexibly set different hash chain length d values, so as to make a trade-off between length and complexity. For example, when d = 15 is set, the length of public key and signature will be about 4 times shorter, but the complexity of signature verification will increase by 4 times. This is essentially a trade-off between Bitcoin stack space and script size. Lamport signature can be regarded as a special case of Winternitz signature when d = 1.
Currently, the BitVM2 library implements Winternitz signature based on Blake3's hash function. The signature length corresponding to a single bit is about 26 bytes. It can be seen that the cost of introducing state through bit commitment is expensive. Therefore, in the BitVM2 project implementation, the message is first hashed to obtain a 256-bit hash value, and then the hash value is bit committed, thereby saving overhead, rather than directly committing to each bit of the original longer message.
2.3 Taproot: Breaking through the script space limitation
The Bitcoin Taproot soft fork upgrade activated in November 2021 includes 3 proposals: Schnorr Signature (BIP 340), Taproot (BIP 341) and TapScript (BIP 342). A new transaction type, Pay-to-Taproot (P2TR) transactions, was introduced. P2TR transactions combine the advantages of Taproot, MAST (Merkle Abstract Syntax Tree) and Schnorr signatures to create a more private, flexible and scalable transaction format.
P2TR supports two spending methods: spending based on key path or script path.
According to the provisions in Taproot (BIP 341), when spending by script path, the maximum length of the corresponding Merkle path does not exceed 128. This means that the number of tapelafs in the taptree does not exceed 2128. Since the segwit upgrade in 2017, the Bitcoin network has measured block size in weight units, supporting a maximum of 4 million weight units (about 4MB). When a P2TR output is spent through a script path, it actually only needs to reveal a single tapelaf script, that is, the block is packaged with a single tapelaf script. This means that for P2TR transactions, the maximum script size for each tapelaf is about 4MB. However, in Bitcoin's default policy, many nodes only forward transactions smaller than 400K. If larger transactions want to be packaged, they need to cooperate with miners.
The script space premium brought by Taproot makes it more valuable to use existing opcodes to simulate cryptographic operations such as multiplication and hashing.
When building verifiable computations based on P2TR, the corresponding script size is no longer limited to 4MB. Instead, the computation can be divided into multiple sub-functions and distributed across multiple tapeleafs, thus breaking through the 4MB script space limit. In fact, the size of the Groth16 verifier algorithm currently implemented in BitVM2 is as high as 2GB. However, it can be divided and distributed across about 1,000 tapeleafs, and combined with bit commitment, the integrity and correctness of the entire computation can be constrained by constraining the consistency between the input and output of each sub-function.
2.4 Connector output: Breaking through the UTXO spending restrictions
Bitcoin currently provides two native spending methods for a single UTXO: spending by script or spending by public key. Therefore, as long as the corresponding correct public key signature is provided or the script conditions are met, the UTXO can be spent. The two UTXOs can be spent independently, and no restrictive measures can be added to constrain the two UTXOs so that they can only be spent if some additional conditions are met.
However, Burak, the founder of the Ark protocol, cleverly used the SIGHASH flag to implement connector output. Specifically, Alice can create a signature to send her BTC to Bob. However, since the signature can commit to multiple inputs, Alice can set her signature to be conditional: the signature is valid for the Take_tx transaction if and only if the transaction consumes the second input. The second input is called a connector, which connects UTXO A and UTXO B. In other words, the Take_tx transaction is valid if and only if UTXO B is not spent by Challenge_tx. Therefore, by destroying the connector output, the Take_tx transaction can be blocked from taking effect.
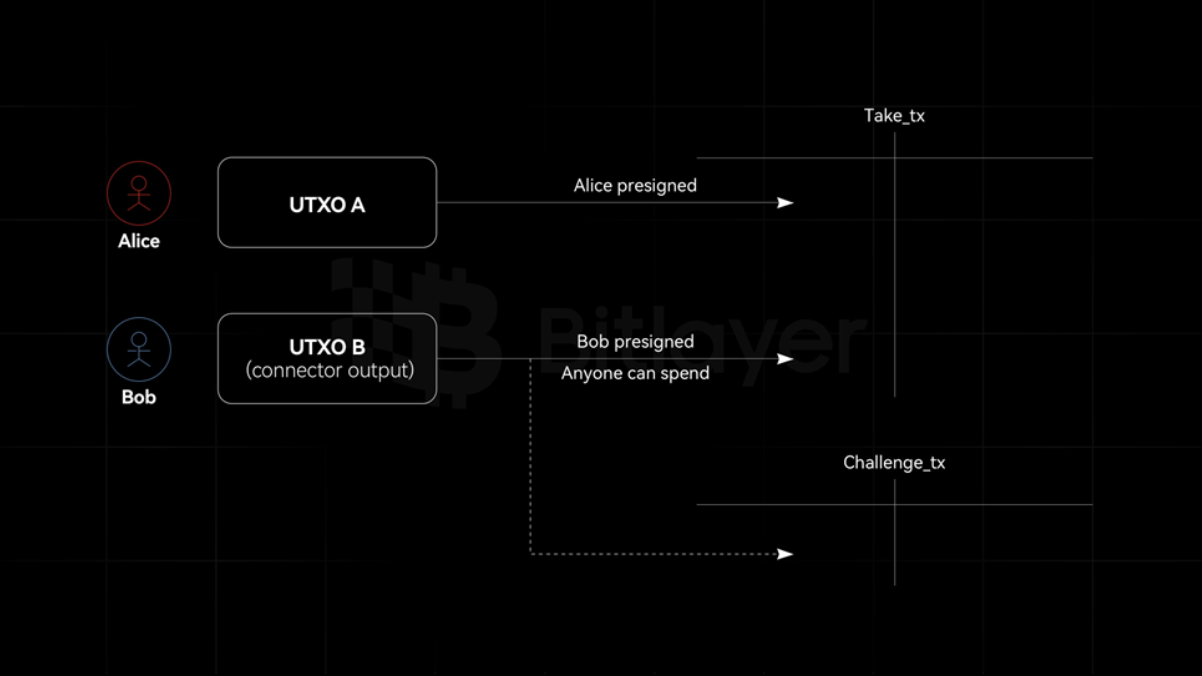
Figure 1: Schematic diagram of connector output
In the BitVM2 protocol, the connector output acts as an if...else function. Once a connector output is spent by a transaction, it cannot be spent by another transaction to ensure its exclusive spending. In actual deployment, in order to reserve the challenge response cycle, an additional UTXO with timelock is introduced. In addition, the corresponding connector output can also set different spending strategies as needed, such as setting the challenge transaction to be spendable by anyone, and setting the response transaction to be spendable only by the operator or by anyone after the expiration date.
2.5 Contract: Breaking through the pre-signing restrictions
Currently, Bitcoin scripts mainly restrict the conditions for unlocking, but do not restrict how the UTXO can be further spent. The reason is that Bitcoin scripts cannot read the content of the transaction itself, that is, they cannot realize transaction introspection. If Bitcoin scripts can check any content of the transaction (including output), the contract function can be realized.
The current contract implementation methods can be divided into two categories:
Pre-signing: Based on the existing Bitcoin scripting capabilities, a pre-determined contract with limited functions is constructed through pre-signing. That is, all possible future transactions are designed and signed in advance, locking the participants into specific private keys and rates. Some schemes even require participants to generate short-term private keys for all pre-signed transactions. When the pre-signing is completed, these short-term private keys are securely deleted, making it impossible for attackers to obtain the short-term private keys and steal funds. However, the above process needs to be repeated every time a new participant is added or an operation is updated, resulting in heavy maintenance costs. For example, the Lightning Network implements 2-party contracts through pre-signing, and with the help of hash time lock (HTLC) technology, it realizes the routing function of multiple 2-party contracts, thereby realizing a trust-minimized expansion strategy. However, the Lightning Network requires pre-signing multiple transactions and is limited to two parties, which is a bit cumbersome; in BitVM1, hundreds of transactions need to be pre-signed each time initialization, and in the optimized BitVM2, the number of transactions that need to be pre-signed each time initialization is also dozens. Whether it is BitVM1 or BitVM2, only the operator who participates in the pre-signing is eligible for reimbursement. If there are n participants involved in pre-signing, and each participant needs to pre-sign m transactions, the pre-signing complexity of each participant will be n ∗ m.
Introducing contract opcodes: Introducing new contract function opcodes can significantly reduce the complexity of communication and maintenance costs between contract participants, thereby introducing a more flexible contract implementation method for Bitcoin. For example, OP_CAT: used to concatenate byte strings. Although its function is very simple, it is very powerful and can significantly reduce the complexity of BitVM; OP_TXHASH: can control the actions within the contract with better granularity. If used in BitVM, it can support a larger set of operators, thereby greatly improving BitVM's security assumptions and minimizing its trust. In addition, the pre-signing method is destined to the BitVM design, in which the operator can only adopt the advance payment reimbursement process, and the efficiency of capital utilization is low; and through the new contract opcode, it is possible to realize the payment directly from the peg-in fund pool to the payer, further improving the efficiency of funds. Therefore, the flexible contract model will effectively break through the traditional pre-signing restrictions.
3 Bitcoin Layer2 Expansion: Proof of Validity and Proof of Fraud
Both validity proof and fraud proof can be used for Bitcoin L2 expansion. The main differences between the two are shown in Table 2.
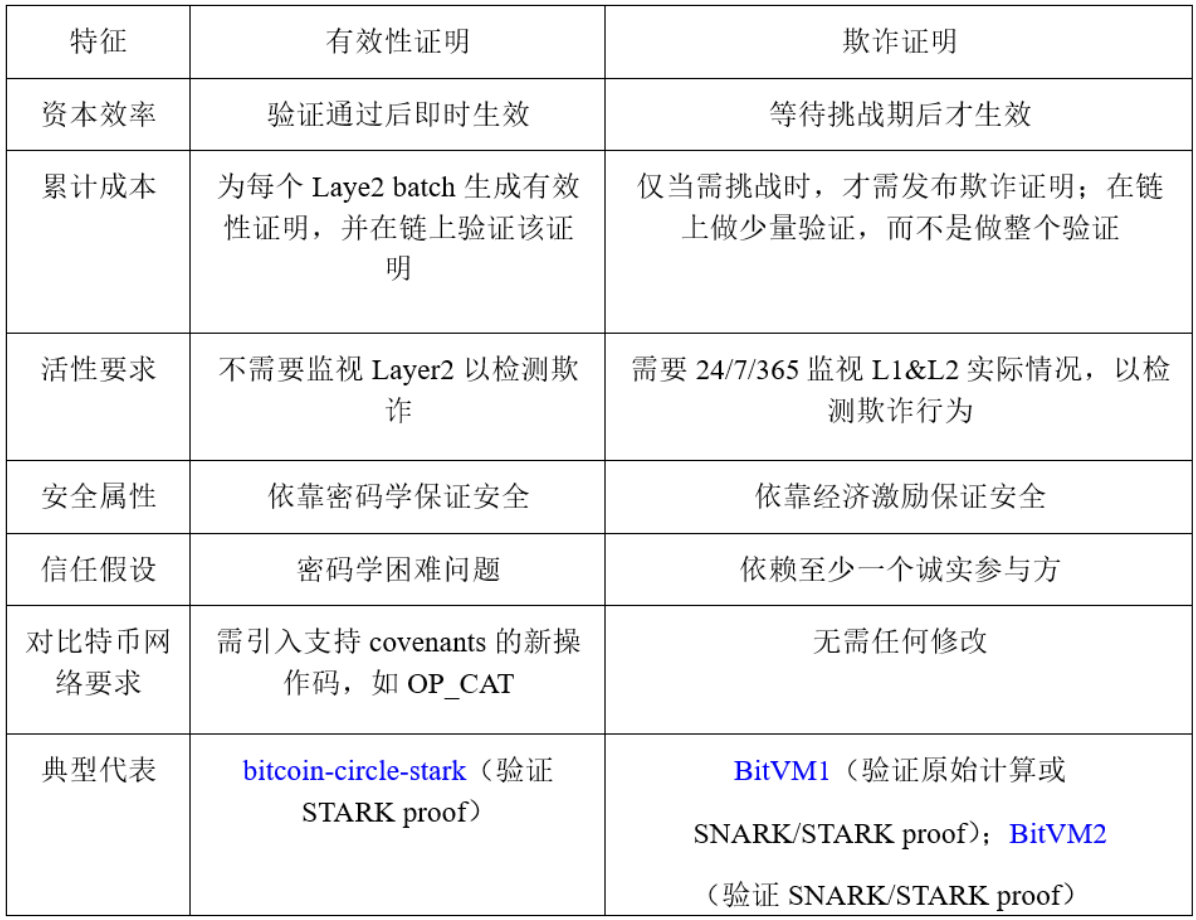
Table 2: Validity Proof and Fraud Proof
Based on bit commitment, taproot, pre-signature and connector output, a Bitcoin-based fraud proof can be constructed. Based on taproot, by introducing contract opcodes such as OP_CAT, a Bitcoin-based validity proof can be constructed. In addition, depending on whether Bob has an access system, fraud proofs can be divided into permissioned fraud proofs and permissionless fraud proofs. Among them, in the permissioned fraud proof, only a specific group can initiate a challenge as Bob, while in the permissionless fraud proof, any third party can initiate a challenge as Bob. The security of the permissionless type is better than that of the permissioned type, which can reduce the risk of collusion among the permitted participants.
According to the number of challenge-response interactions between Alice and Bob, fraud proofs can be divided into one-round fraud proofs and multi-round fraud proofs, as shown in Figure 2.
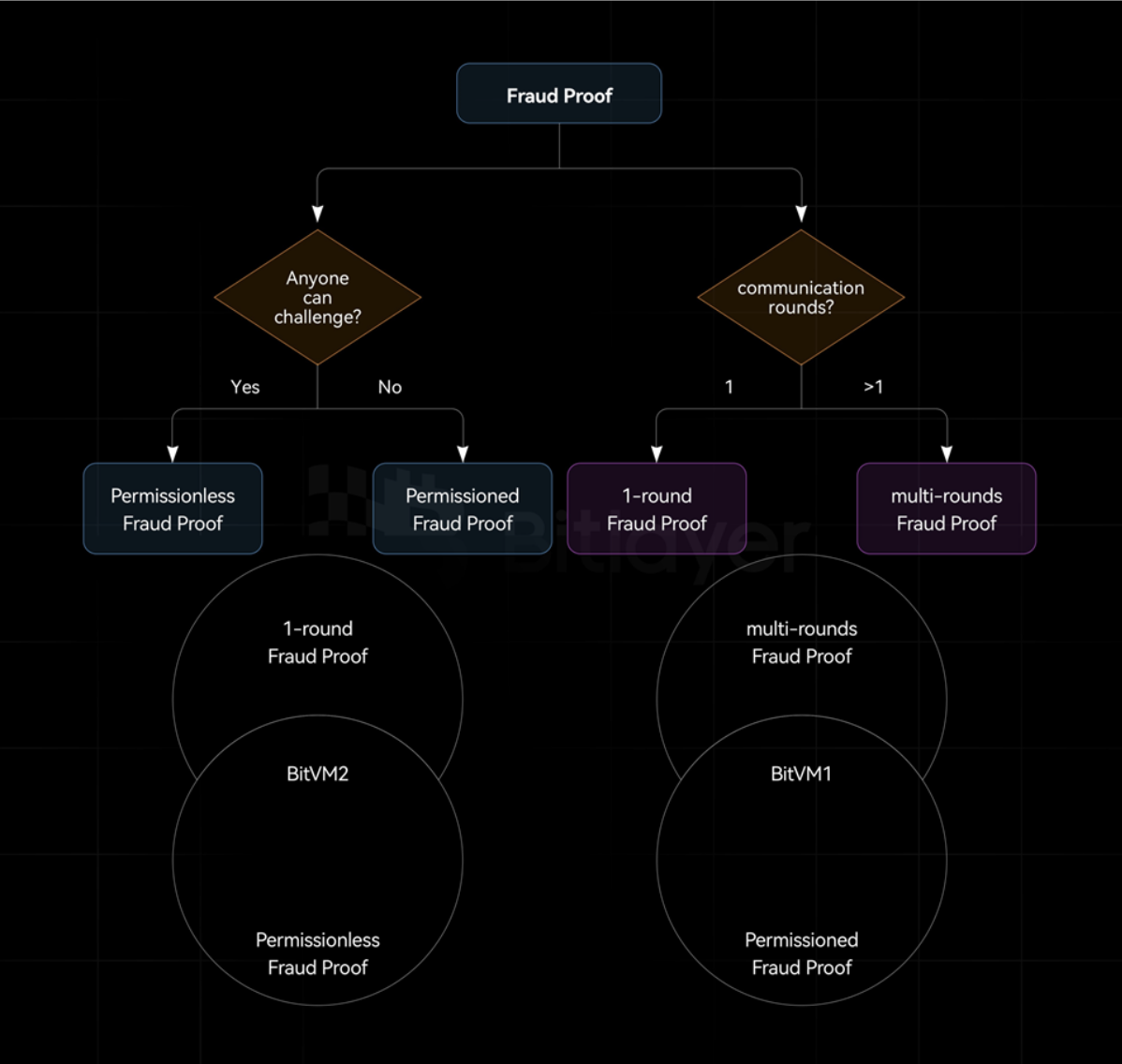
Figure 2: One-round fraud proof vs. multi-round fraud proof
As shown in Table 3, fraud proof can be implemented through different interaction models, including one-round interaction model and multi-round interaction model.
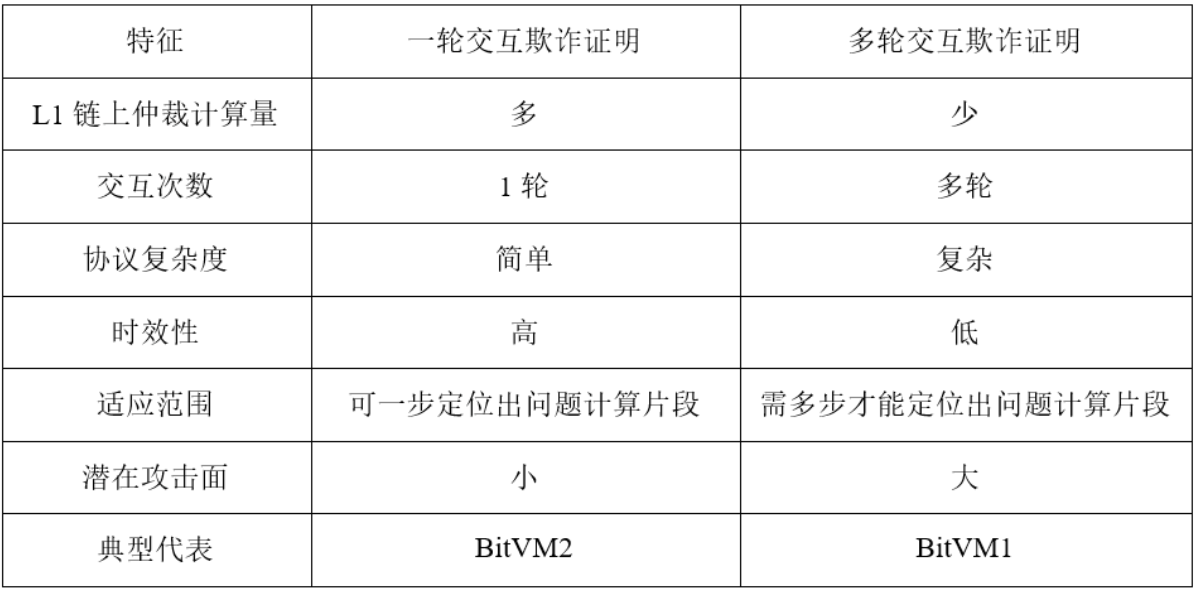
Table 3: One-round interaction and multiple-round interaction
Under the Bitcoin Layer2 expansion paradigm, BitVM1 uses a multi-round fraud proof mechanism, BitVM2 uses a single-round fraud proof mechanism, and bitcoincircle stark uses validity proof. Among them, BitVM1 and BitVM2 can be implemented without making any changes to the Bitcoin protocol, while bitcoin-circle stark needs to introduce a new opcode OP_CAT.
For most computing tasks, Bitcoin signet, testnet and mainnet cannot be fully expressed by a 4MB script, and the script split technology is required - that is, the script that expresses the complete calculation is divided into chunks smaller than 4MB and distributed to each tapelaf.
3.1 Multi-round Fraud Proofs on Bitcoin
As shown in Table 3, multi-round fraud proofs are suitable for scenarios where you want to reduce the amount of on-chain arbitration computation and/or cannot locate the problematic computation fragment in one step. As the name suggests, multi-round fraud proofs require multiple rounds of interaction between the prover and the verifier to locate the problematic computation fragment, and then conduct arbitration based on the located computation fragment.
Robin Linus's early BitVM white paper (often referred to as BitVM1) used multiple rounds of fraud proofs. Assuming that each round of challenge period is one week, and the binary search method is used to locate the problematic computational fragment, the on-chain challenge response cycle for Groth16 Verifier will be as high as 30 weeks, which is extremely time-sensitive. Although there are teams currently researching n-ary search methods that are more efficient than the binary search method, their timeliness is still much lower than the 2-week cycle in a round of fraud proofs.
At present, multi-round fraud proofs under the Bitcoin paradigm all use permissioned challenges, while one-round fraud proofs implement permissionless challenges, which reduces the risk of collusion among participants and provides higher security. To this end, Robin Linus took full advantage of taproot and optimized BitVM1. Not only did he reduce the number of interaction rounds to 1, he also expanded the challenge method to permissionless, but at the cost of increasing the amount of on-chain arbitration calculations.
3.2 A round of fraud proofs on Bitcoin
The fraud proof can be verified with only one interaction between the prover and the verifier. In this model, the verifier only needs to issue a challenge once, and the prover only needs to respond once. In the response, the prover needs to provide a proof that his calculation is correct. If the verifier can find inconsistencies in the proof, the challenge succeeds, otherwise the challenge fails. The characteristics of a round of interactive fraud proof are shown in Table 3.
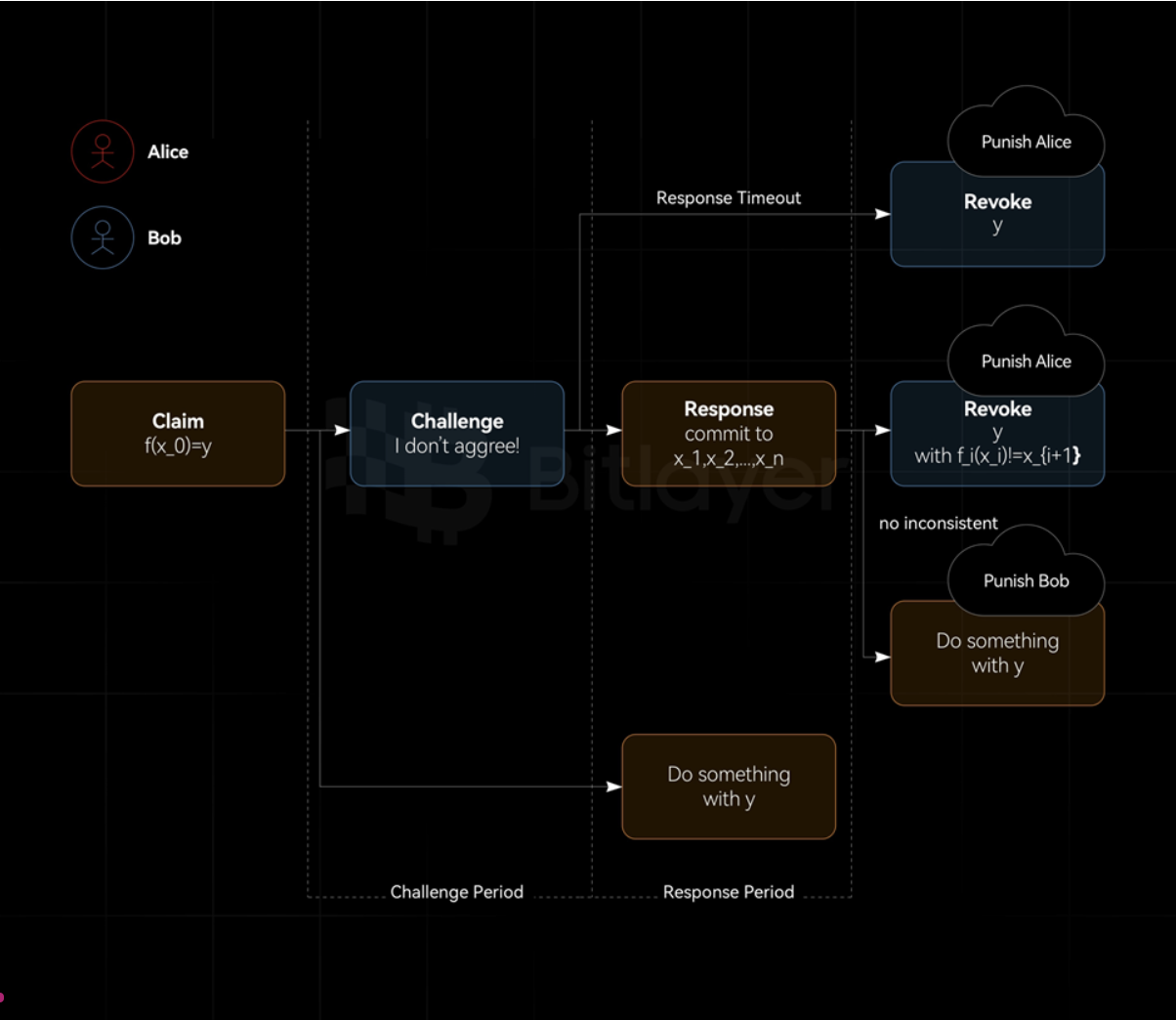
Figure 3: One round of fraud proofs
In the technical white paper BitVM2: Bridging Bitcoin to Second Layers released by Robin Linus on August 15, 2024, a method similar to Figure 3 was used to implement the BitVM2 cross-chain bridge using a round of fraud proofs.
3.3 Bitcoin + OP_CAT to achieve validity proof
OP_CAT was part of the scripting language when Bitcoin was first released, but was disabled in 2010 due to security vulnerabilities. However, the Bitcoin community has been discussing activating it for several years. Currently, OP_CAT has been assigned number 347 and has been enabled on the Bitcoin signet.
The main function of OP_CAT is to combine two elements in the stack and push the combined result back to the stack. This feature opens up contracts and STARK Verifier on Bitcoin:
Covenants: Andrew Poelstra proposed CAT and Schnorr Tricks I, using OP_CAT and Schnorr tricks to implement covenants on Bitcoin. The Schnorr algorithm is a digital signature for P2TR output types; for other output types, similar ECDSA tricks can be used, see Covenants with CAT and ECDSA. With the help of OP_CAT covenants, the STARK Verifier algorithm can be split into multiple transactions to gradually verify the entire STARK proof.
STARK Verifier: STARK Verifier essentially concatenates data together and hashes it. Unlike algebraic operations, hashing is a native Bitcoin script operation, which can save a lot of overhead. Take OP_SHA256 as an example. The native method is only one opcode, while the simulated method requires hundreds of K. The main hashing operations in STARK are the verification of Merkle paths and the Fiat-Shamir transformation. Therefore, OP_CAT is very friendly to the STARK Verifier algorithm.
3.4 Bitcoin Script Split Technology
Although after SNARK/STARK proof, the amount of computation required to run the corresponding verifier algorithm to verify the proof is much less than the amount of computation required to directly run the original calculation f. However, when it is converted to implement the verifier algorithm with Bitcoin script, the amount of script required is still huge. Currently, based on the existing Bitcoin opcodes, after optimization, the implemented Groth16 verifier script size and Fflonk verifier script size are still greater than 2GB. However, the size of a single Bitcoin block is only 4MB, and the entire verifier script cannot be run in a single block. However, since the taproot upgrade, Bitcoin supports script execution by tapeleaf, which can divide the verifier script into multiple chunks, and then build a taptree with each chunk as a tapeleaf. Between each chunk, bit commitment is used to ensure the consistency of values between chunks.
In the presence of an OP_CAT contract, the STARK Verifier can be split into multiple standard transactions of less than 400KB, so that the entire STARK validity proof can be verified without the need to collaborate with miners.
This section focuses on the relevant Split technology of Bitcoin Script in the existing case without introducing or activating any new opcodes.
When splitting scripts, the following dimension information needs to be balanced:
The size of a single chunk script shall not exceed 4MB and must include space for input bit commitment scripts, transaction signatures, etc.
The maximum size of a single chunk stack is no more than 1000. Therefore, only the required elements should be kept on each chunk stack, so as to reserve enough stack space to serve the script size optimization. Because the Bitcoin transaction fee does not depend on the stack size used.
Bit commitment on Bitcoin is expensive. So currently 1 bit corresponds to 26 bytes, and the number of input and output bits between 2 adjacent chunks should be minimized.
To facilitate auditing, the function of each chunk should be as clear as possible.
Currently, script segmentation methods are mainly divided into the following three categories:
Automatic segmentation: Based on the stack size and script size, find a segmentation method that minimizes the stack size while keeping the script size around 3MB. The advantages of this method are that it is independent of the specific verifier algorithm and can be extended to segment scripts for any calculation. The disadvantages are: (1) The entire block of logic needs to be marked separately. For example, the OP_IF code block cannot be segmented, otherwise the script execution result after segmentation will be incorrect; (2) The chunk execution result may correspond to multiple elements on the stack. The number of stack elements that need to apply bit commitment needs to be marked based on the actual calculation logic; (3) The logical functions implemented by each chunk script are poorly readable, which is not conducive to auditing; (4) The stack may contain elements that are not needed by the next chunk, wasting stack space.
Functional segmentation: segmentation is based on each functional sub-function in the calculation. The input and output values of the sub-function are clear. While segmenting the script, the bit commitment script required by each chunk is also implemented, so that the total script size of the final chunk is less than 4MB and the stack size is less than 1000. The advantages are: clear functions, clear logic of a single chunk, good readability, and easy auditing. The disadvantages are: the expression of the original calculation logic does not match the expression of the script-level logic. The original calculation sub-function may be optimal, but it does not mean the script-level is optimal.
Manual segmentation: The script segmentation point is not in the functional sub-function, but is manually set. It is especially suitable for the case where the size of a single sub-function is greater than 4MB. The advantages are: the heavy script size sub-function, such as the Fq12 related calculation sub-function, can be manually segmented; the logic of a single chunk is clear, the readability is good, and it is easy to audit. The disadvantages are: due to the limitation of manual tuning capabilities, when the overall script is optimized, the previously set manual segmentation points may not be optimal and need to be readjusted.
For example, after multiple rounds of optimization, the script size of the Groth16 verifier has been reduced from about 7GB to about 1.26GB. In addition to this overall computational optimization, each chunk can also be optimized separately to make full use of the stack space. For example, by introducing a better algorithm based on the lookup table and dynamically loading and unloading the lookup table, the script size of each chunk can be further reduced.
The computational cost and operating environment of the web2 programming language are completely different from those of Bitcoin scripts, so for Bitcoin script implementations of various algorithms, simply translating existing implementations is not feasible. Therefore, the following optimizations need to be considered for Bitcoin scenarios:
Finding an algorithm with optimal memory locality, even at the expense of some computational effort, can reduce the number of input and output bits between chunks, thereby reducing the amount of data required to commit to assertTx transactions in the BitVM2 design.
By taking advantage of the commutativity of related operations (such as logical operations), x&y = y&x, almost half of the lookup table is saved.
Currently, the amount of scripts corresponding to Fq12 operations is very large. We can consider using Fiat-Shamir, Schwartz-Zipple and polynomial commitment schemes to significantly reduce the computational complexity of Fq12 extended domain operations.
4 Summary
This article first introduces the Bitcoin script restrictions, and introduces how to break through the UTXO stateless restrictions using Bitcoin commitments, break through the script space restrictions using Taproot, break through the UTXO spending restrictions using connector outputs, and break through the pre-signing restrictions using contracts. Then, the characteristics of fraud proofs and validity proofs, the characteristics of permissioned fraud proofs and permissionless fraud proofs, the characteristics of one-round fraud proofs and multi-round fraud proofs, and Bitcoin script segmentation technology are comprehensively sorted out and summarized.