Faster block/blob propagation in Ethereum
Acknowledgements to @n1shantd, @ppopth and Ben Berger for discussions and feedback on this writeup and @dankrad for many useful discussions.
Abstract
We propose a change on the way we broadcast and transfer blocks and blobs in the P2P network, by using random linear network coding. We show that we can theoretically distribute the block consuming 5% of the bandwidth and with 57% of the number of network hops (thus half the latency per message) of the time it takes on the current gossipsub implementation. We provide specific benchmarks to the computational overhead.
Introduction
The current gossipsub mechanism for distribution of blocks roughly works as follows. The proposer picks a random subset (called its Mesh) of D=8 peers among all of its peers and broadcasts its block to them. Each peer receiving a block performs some very fast preliminary validation: mostly signature verification, but most importantly not including state transition nor execution of transactions. After this fast validation, the peer rebroadcasts its block to another D peers. There are two immediate consequences from such a design:
- Each hop adds at least the following delay: one full block transfer from one peer to the next one (including both network ping latency, essentially bandwidth independent, plus transfer of the full block, bound by bandwidth).
- Peers broadcast unnecessarily a full block to other peers that have already received the full block.
We propose to use random linear network coding (RLNC) at the broadcast level. With this coding, the proposer would split the block in N chunks (eg. N=10 for all simulations below) and instead of sending a full block to ~8 peers, it will send a single chunk to ~40 peers (not one of the original chunks, but rather a random linear combination of them, see below for privacy considerations). Peers still need to download a full block, or rather N chunks, but they can get them in parallel from different peers. After they have received these N chunks that each is a random linear combination of the original chunks composing the original block, peers need to solve a linear system of equations to recover the full block.
A proof of concept implementation highlights the following numbers
- Proposing a block takes extra 26ms that are CPU bound and can be fully parallelized to less than 2ms on a modern laptop (Apple M4 Pro)
- Verifying each chunk takes 2.6ms.
- Decoding the full block takes 1.4ms.
- With
10chunks andD=40, each node sends half the data than with current gossipsub and the network broadcasts a 100KB block in half the time with benefits increasing with block size.
The protocol
For an in-depth introduction to network coding and we refer the reader to loc. cit. and this textbook. We here mention minimal implementation details for the proof of concepts benchmarks cited above. In the case of block propagation (~110KB), latency or number of network hops dominate the propagation time, while in the case of large messages like blobs in full DAS, bandwidth dominates the propagation time.
We consider a finite field \mathbb{F}_pFp of prime characteristic. In the example above we choose the Ristretto scalar base field as implemented by the curve25519-dalek rust crate. The proposer takes a block, which is an opaque byte slice, and interprets it as a vector of elements in \mathbb{F}_pFp. A typical ethereum block is about B = 110KBB=110KB at the time of writing, given that each Ristretto scalar takes a little less than 32 bytes to encode, a block takes about B/32 = 3520B/32=3520 elements of \mathbb{F}_pFp. Dividing into N=10 chunks, each chunk can be viewed as a vector in \mathbb{F}_p^{M}FMp, where M \sim 352M∼352. The block is thus viewed as NN vectors v_i \in \mathbb{F}^M_pvi∈FMp, i=1,...,Ni=1,...,N. The proposer chooses a subset of D\sim 40D∼40 peers at random. To each such peer it will send one vector of \mathbb{F}_p^MFMp together with some extra information to validate the messages and prevent DOS on the network. We explain the proposer
The Proposer
We will use Pedersen commitments to the Ristretto elliptic curve EE as implemented by the above mentioned rust crate. We assume that we have already chosen at random a trusted setup of enough elements G_j \in EGj∈E, j = 1, ..., Kj=1,...,K with K \gg MK≫M. We choose a standard basis \{e_j\}_{j=1}^M{ej}Mj=1 for \mathbb{F}_p^MFMp. So each vector v_ivi can be written uniquely as
$$ v_i = \sum_{j=1}^M a_{ij} e_j, $$
for some scalars a_{ij} \in \mathbb{F}_paij∈Fp. To each vector v_ivi we have a Pedersen commitment
$$ C_i = \sum_{j=1}^M a_{ij}G_j \in E. $$
Finally for each peer in the subset of size D \sim 40D∼40 the proposer chooses uniformly random a collection of scalars b_ibi, i=1, ...,Ni=1,...,N and sends the following information to the peer
- The vector v = \sum_{i=1}^N b_i v_i \in \mathbb{F}_p^Mv=∑Ni=1bivi∈FMp. This is of size 32M32M bytes and it’s the content of the message.
- The NN commitments C_iCi, i=1,...,Ni=1,...,N. This is 32N32N bytes.
- The NN coefficients b_ibi, i=1, ...,Ni=1,...,N. This is 32N32N bytes.
- A BLS signature to the hash of the NN commitments C_1 || C_2 || ... || C_NC1||C2||...||CN, this is 9696 bytes.
A signed message is the collection of elements 1–4 above. We see that there are 64N \sim 64064N∼640 extra bytes sent on each message as a sidecar.
Receiving Peers
When a peer receives a message as in the previous section, the verification goes as follows
- It verifies that the signature is valid for the proposer and the hash of the receiving commitments.
- It writes the receiving vector v = \sum_{j=1}^M a_j e_jv=∑Mj=1ajej and then computes the Pedersen commitment C = \sum_{j=1}^M a_j G_jC=∑Mj=1ajGj.
- The received coefficients b_ibi are a claim that v = \sum_{i=1}^N b_i v_iv=∑Ni=1bivi. The peer computes C'= \sum_{i=1}^N b_i C_iC′=∑Ni=1biCi, and then verifies that C = C'C=C′.
Peers keep track of the messages that they have received, say they are the vectors w_iwi, i = 1,...,Li=1,...,L for L < NL<N. They generate a subspace W \subset \mathbb{F}_p^MW⊂FMp. When they receive vv, they first check that if this vector is in WW. If it is, then they discard it as this vector is already a linear combination of the previous ones. The key of the protocol is that this is very unlikely to happen (for the numbers above the probability of this happening is much less than 2^{-256}2−256). As a corollary of this, when the node has received NN messages, then it knows that it can recover the original v_ivi, and thus the block, from the messages w_iwi, i=1,...,Ni=1,...,N.
Notice also that there is only one signature verification that is needed, all incoming messages have the same commitments C_iCi and the same signature over the same set of commitments, thus the peer may cache the result of the first valid verification.
Sending Peers
Peers can send chunks to other peers as soon as they receive one chunk. Suppose a node holds w_iwi, i=1,...,Li=1,...,L with L \leq NL≤N as in the previous section. A node also keeps track of the scalar coefficients they received, thus they know the chunks they hold satisfy
$$ w_i = \sum_{j=1}^N b_{ij} v_j \quad \forall i,$$
for some scalars b_{ij} \in \mathbb{F}_pbij∈Fp they save in their internal state. Finally, nodes also keep the full commitments C_iCi and the signature from the proposer that they have validated when they validated the first chunk they received.
The procedure by which a node sends a message is as follows.
- They choose randomly LL scalars \alpha_i \in \mathbb{F}_pαi∈Fp, i=1,...,Li=1,...,L.
- They form the chunk w = \sum_{i=1}^L \alpha_i w_iw=∑Li=1αiwi.
- They form the NN scalars a_jaj, i=1,...,Ni=1,...,N by
$$ a_j = \sum_{i=1}^L \alpha_i b_{ij}, \quad \forall j=1,…,N. $$
The message they send consists of the chunk ww, the coefficients a_jaj and the commitments C_iCi with the signature from the proposer.
Benchmarks
The protocol has some components that are in common with gossipsub, for example the proposer needs to make one BLS signature and the verifier has to check one BLS signature. We record here the benchmarks of the operations that need to be carried in addition to the usual gossipsub operations. These are the CPU overhead that the protocol has on nodes. Benchmarks have been carried on a Macbook M4 Pro laptop and on an Intel i7-8550U CPU @ 1.80GHz.
Parameters for these benchmarks were N=10N=10 for the number of chunks and the total block size was considered to be 118.75KB. All benchmarks are single threaded and all can be parallelized
Proposer
The proposer needs to perform NN Pedersen commitments. This was benchmarked to be
| Timing | Model |
|---|---|
| [25.588 ms 25.646 ms 25.715 ms] | Apple |
| [46.7ms 47.640 ms 48.667 ms] | Intel |
Nodes
A receiving node needs to compute 1 Pedersen commitment per chunk and perform a corresponding linear combination of the commitments supplied by the proposer. The timing for these were as follows
| Timing | Model |
|---|---|
| [2.6817 ms 2.6983 ms 2.7193 ms] | Apple |
| [4.9479 ms 5.1023 ms 5.2832 ms] | Intel |
When sending a new chunk, the node needs to perform a linear combination of the chunks it has available. Timing for these were as follows
| Timing | Model |
|---|---|
| [246.67 µs 247.85 µs 249.46 µs] | Apple |
| [616.97 µs 627.94 µs 640.59 µs] | Intel |
When decoding the full block after receiving NN chunks, the node needs to solve a linear system of equations. Timings were as follows
| Timing | Model |
|---|---|
| [2.5280 ms 2.5328 ms 2.5382 ms] | Apple |
| [5.1208 ms 5.1421 ms 5.1705 ms] | Intel |
Overall CPU overhead.
The overall overhead for the proposer on the Apple M4 is 26ms single threaded while for the receiving nodes it is 29.6ms single threaded. Both processes are fully parallelizable. In the case of the proposer, it can compute each commitment in parallel, and in the case of the receiving node these are naturally parallel events since the node is receiving the chunks in parallel from different peers. Running these process in parallel on the Apple M4 leads to 2.6ms in the proposer side and 2.7ms in the receiving peer. For real life applications it is reasonable to consider these overheads as zero compared to the network latencies involved.
Optimizations
Some premature optimizations that were not implemented consist on inverting the linear system as the chunks come, although the proof of concept cited above does keep the incoming coefficient matrix in Eschelon form. Most importantly, the random coefficients for messages do not need to be in such a large field as the Ristretto field. A small prime field like \mathbb{F}_{257}F257 suffices. However, since the Pedersen commitments take place in the Ristretto curve, we are forced to perform the scalar operations in the larger field. The implementation of these benchmarks chooses small coefficients for the linear combinations, and these coefficients grow on each hop. By controlling and choosing the random coefficients correctly, we may be able to bound the coefficients of the linear system (and thus the bandwidth overhead in sending the blocks) to be encoded with say 4 bytes instead of 32.
The simplest way to perform such optimization would be to work over an elliptic curve defined over \mathbb{F}_qFq with q = p^rq=pr for some small prime pp. This way the coefficients can be chosen over the subfield \mathbb{F}_p \subset \mathbb{F}_qFp⊂Fq.
Privacy considerations the implementation in the PoC linked above considers that each node, including the proposer, picks small coefficients to compound its linear transformation. This allows a peer receiving a chunk with small coefficients to recognize the proposer of the block. Either the optimization above is employed to keep all coefficients small by performing an algorithm like Bareiss’ expansions or we should allow the proposer to choose random coefficients from the field \mathbb{F}_pFp.
Simulations
We performed simulations of block propagation under some simplifying assumptions as follows.
- We choose a random network modeled as a directed graph with 10000 nodes and each node having DD peers to send messages to. DD is called the Mesh size in this note and was chosen varying on a large range from 3 to 80.
- Peers where chosen randomly and uniformly on the full node set.
- Each connection was chosen with the same bandwidth of XX MBps (this is typically assumed to be X=20X=20 in Ethereum but we can leave this number as a parameter)
- Each network hop, incurs in an extra constant latency of LL milliseconds (this is typically measured as L=70L=70 but we can leave this number as a parameter)
- The message size is assumed to be BB KB in total size.
- For the simulation with RLNC, we used N=10N=10 chunks to divide the block.
- Each time a node would send a message to a peer that would drop it because of being redundant (for example the peer already had the full block), we record the size of the message as wasted bandwidth.
Gossipsub
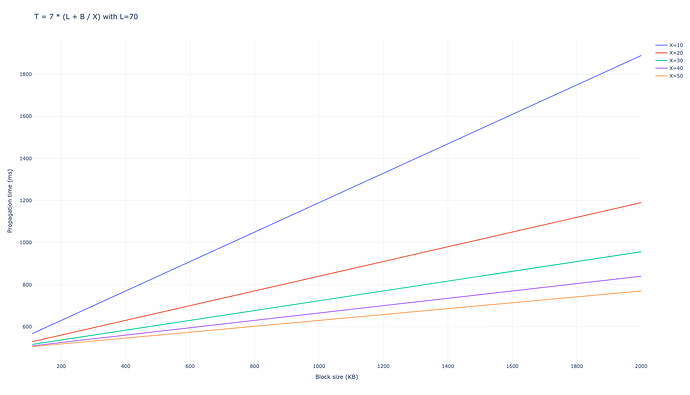
We used the number of peers to send messages D=6D=6. We obtain that the network takes 7 hops in average to propagate the full block to 99% of the network, leading to a total propagation time of
$$ T_{\mathrm{gossipsub, D=6}} = 7 \cdot (L + B/X), $$
in milliseconds.
With D=8D=8 the result is similar
$$ T_{\mathrm{gossipsub, D=8}} = 6 \cdot (L + B/X), $$
The wasted bandwidth is 94,060 \cdot B94,060⋅B for D=6D=6 and 100,297 \cdot B100,297⋅B for D=8D=8.
For low values of BB, like the current Ethereum blocks, latency dominates the propagation, while for larger values, for example propagating blobs after peer-DAS, bandwidth becomes the main factor.
RLNC
Single chunk per peer
With random linear network coding we can use different strategies. We simulated a system in which each node will only send a single chunk to all of the peers in their mesh of size DD, this way we guarantee that the latency incurred is the same as in gossipsub: a single latency cost of LL milliseconds per hop. This requires the mesh size to be considerably larger than NN, the number of chunks. Notice that for a gossipsub mesh size of D_{gossipsub}Dgossipsub (for example 88 in current Ethereum), we would need to set D_{RLNC} = D_{gossipsub} \cdot NDRLNC=Dgossipsub⋅N to consume the same bandwidth per node, this would be 8080 with the current values.
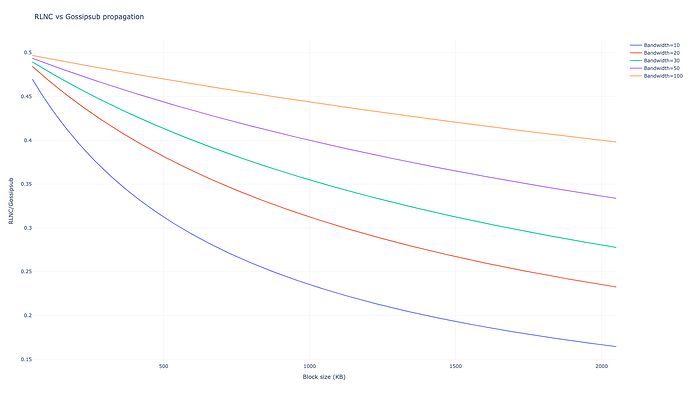
With a much more conservative value of half this bandwidth, that is D=40D=40 we obtain
$$T_{RLNC, D=40} = 4 \cdot \left(L + \frac{B}{10 X} \right), $$
with a wasted bandwidth of 29,917\cdot B29,917⋅B. Assuming the same bandwidth as today we obtain with D=80D=80 we get the impressive
$$T_{RLNC, D=80} = 3 \cdot \left(L + \frac{B}{10 X} \right), $$
with a wasted bandwidth of 28,124\cdot B28,124⋅B, which is 28% of the corresponding wasted bandwidth in gossipsub.
Differences
For the same bandwidth sent per node, we see that the propagation time differs both by dividing the latency in two (there are 3 hops vs 6) and by propagating the block faster consuming a tenth of the bandwidth per unit of time. In addition the wasted bandwidth by superfluous messages gets slashed to 28% of the gossipsub wasted messages. Similar results are obtained for propagation time and wasted bandwidth but reducing the bandwidth sent per node by a half.
In the lower block size end, latency is dominant and the 3 hops vs 6 on gossipsub make most of the difference, in the higher block size end, bandwidth performance is dominant. For much larger blocksizes CPU overhead in RLNC gets worse, but given the order of magnitude of the transmission times, these are negligible.
Multiple chunks per peer
In the single chunk per peer approach in production, nodes with higher bandwidth could choose to broadcast to more peers. At the node level this can be implemented by simply broadcasting to all the current peers and node operators would simply chose the number of peers via a configuration flag. Another approach is to allow nodes to send multiple chunks to a single peer, sequentially. The results of these simulations are exactly the same as the above, but with much lower DD as expected. For example with D=6D=6, which would never broadcast a full block in the case of a single chunk sent per peer. The simulation takes 10 hops to broadcast the full block. With D=10D=10 the number of hops is reduced to 9.
Conclusions, omissions and further work
Our results show that one expects considerable improvement in both block propagation time and bandwidth usage per node if we were to use RLNC over the current routing protocol. These benefits become more apparent the larger the block/blob size or the shorter the latency cost per hop. Implementation of this protocol requires substantial changes to the current architecture and it may entail a new pubsub mechanism altogether. In order to justify this we may want to implement the full networking stack to simulate under Shadow. An alternative would be to implement Reed-Solomon erasure coding and routing, similar to what we do with Peer-DAS. It should be simple to extend the above simulations to this situation, but op. cit already includes many such comparisons.