When I left academia, I promised myself not to write any more papers. But desperate times call for desperate measures! One LVR question bothered me for literally years. Then came along @MartinTassy and solved it. Below is a bit of history & some intuition 1/n

When @jason_of_cs, @ciamac, @Tim_Roughgarden, and @alz_zyd_ first introduced the idea of LVR, they did it in a model without swap fees. This, of course, immediately raised the question: What would the *net* LVR be in a model with swap fees? 2/n moallemi.com/ciamac/papers/lvr...

I enlisted two friends (Dmitry Livdan, UC Berkeley, and Alex Boulatov, HSE University) to prove the following result. The loss of LPs is: * cubic in volatility * inversely related to the swap fee * proportional to sqrt of block time There were however still two issues... 3/n

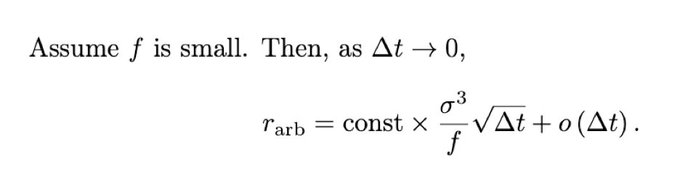
First, our proof was a bit hand-wavy (something something Fokker–Planck equation) or so I understood it to be. Second, I couldn't figure out the exact constant to make the equation work. So naturally I gave up and dropped a twitter thread instead 4/n

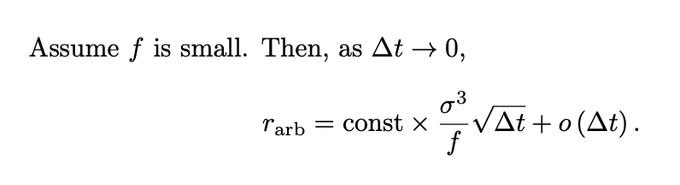
But then @jason_of_cs, @ciamac, @Tim_Roughgarden published their "LVR with fees" piece, which had among other things: * an exact formula for the loss of LPs in the model with fees * a complete proof of the result They were able to accomplish this... 5/n moallemi.com/ciamac/papers/lvr...

with one elegant assumption: that blocks arrive according to a Poisson process. This assumption is descriptive for proof-of-work chains. But most proof-of-stake chains have fixed block times. This got me thinking: holding the average block time fixed, what is the... 6/n

impact of block time uncertainty on the LP losses to arbitrageurs? Basically, we still need to determine that constant! I locked in. I stopped reading to my kids. Canceled gym membership. Told friends that I was having health issues. Asked every stats professor I knew... 7/n

Then I remembered that @MartinTassy and @_Dave__White_ worked on a similar question before but used somewhat different tools. (I do as much as possible in continuous time and then figure out what happens in a nearby discrete model, but they went in the opposite direction) 8/n

So I reached out to Martin. One thing was pretty clear from comparing the models with fixed times and Poisson block arrival. The loss of LPs is the product of: Probability of an arb swap * Loss per arb swap. It turns out that the *probability* of an arb swap... 9/n

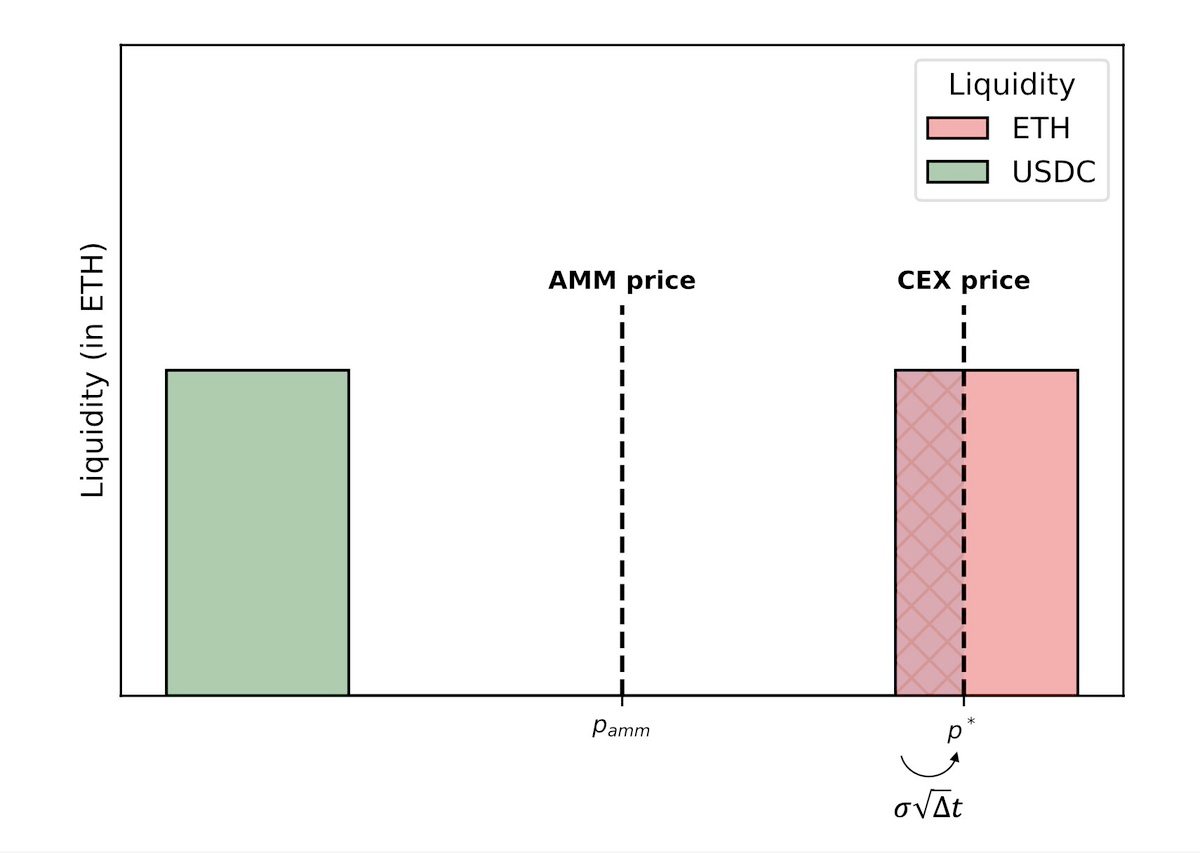
is only a function of the *average* block time. It doesn't matter if blocks arrive at constant intervals or according to the Poisson model. But the loss per arbitrage swap is smaller when block times are fixed. Why? The loss increases in the amount by which CEX price... 10/n

overshoots the bid-ask spread of the DEX during the interblock time. To overshoot, the CEX price first needs to reach the boundary of the spread, and then use the time remaining until the next block to overshoot. In the Poisson model, if the mean block time is 12s... 11/n

and the price reaches the boundary 2s after the previous block, then it still has on average 12s for the overshoot. But with fixed block times, it would only have 10s. In the paper below, Martin and I provide the exact expression for the loss with fixed block times. 12/n

Turns out that the constant we were looking for includes the Riemann zeta function evaluated at 1/2. I feel like we are getting close to connecting AMM research to the Riemann hypothesis, which is pretty impressive given that it all started with xy=k! http:/arxiv.org/pdf/2505.05113