Microsoft's former AI Vice President and Distinguished Scientist Sebastien Bubeck stated that GPT-5 Pro solved an unresolved interval in a mathematical paper from scratch, which shocked him. This discovery led to widespread sharing among experts, with OpenAI's president believing AI might accelerate mathematical research.
Can AI really solve humanity's cutting-edge problems?
Such as the Poincaré conjecture, Maxwell's equations, Fermat's Last Theorem, Riemann hypothesis, and other problems.
Today, this question has an answer.
AI can indeed do it! Completely independently, without referencing any existing human methods.
Last night, GPT-5 Pro could solve a complex mathematical problem from scratch.
And again, it did not use any previous human proof methods.
Moreover, its answer was better than the solution in the paper.
Fortunately for humans, the paper's authors later provided a new method that surpassed the AI.
Sebastien Bubeck is an OpenAI research engineer, previously serving as Microsoft's AI Vice President and Distinguished Scientist.
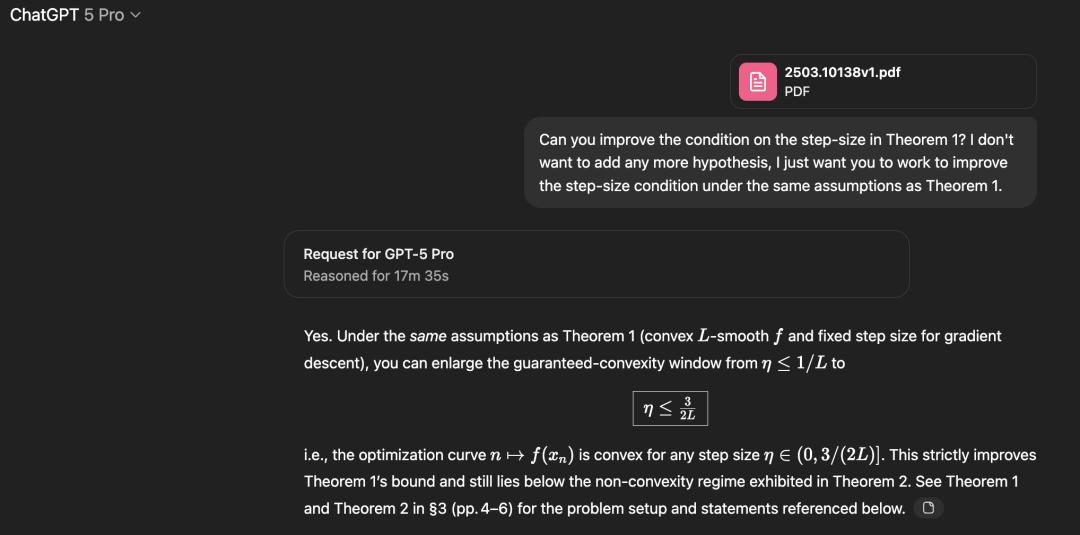
He directly threw a paper at GPT-5 Pro.
This paper studied a very natural problem: Under what conditions does the step size η in gradient descent for smooth convex optimization result in a convex curve of function values at iteration points?
Paper address: https://arxiv.org/pdf/2503.10138v1
In the v1 version of the paper, they proved that if η is less than 1/L (L being smoothness), this property can be obtained.
If η is greater than 1.75/L, the authors constructed a counterexample.
Therefore, the unresolved problem is: What happens in the interval [1/L, 1.75/L]?
First, a simple explanation of this problem.
Gradient descent is like going downhill, where you choose a step size η. L can be understood as the "curvature" of the terrain (the larger it is, the steeper/more sensitive).
The paper is not only concerned with "will it go down" (monotonic descent) but also whether the descent trajectory is "convex": that is, the improvement at each step is not drastically different, not "like a plateau at the beginning and then suddenly a cliff".
This is very useful for knowing when to stop - convexity means becoming increasingly stable, without sudden large drops.
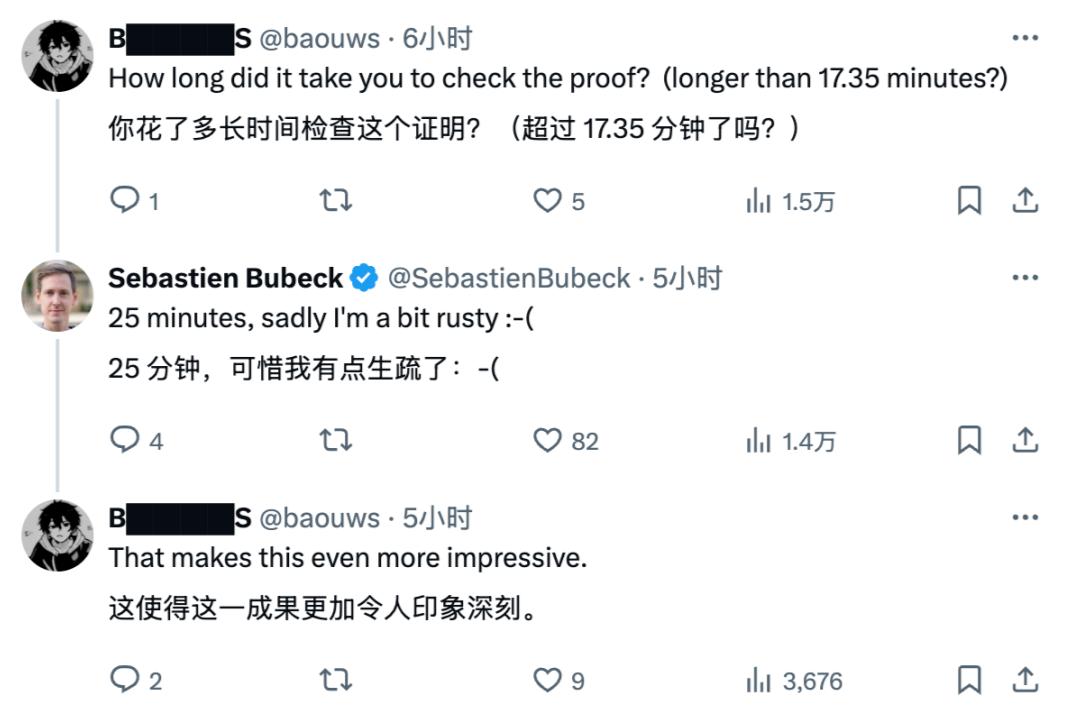
Sebastien used GPT-5 Pro to attack this unresolved interval, and the model pushed the known lower bound from 1/L to 1.5/L.
Here is the proof provided by GPT-5 Pro.
Although initially incomprehensible, the overall proof process looks very elegant.
Sebastien was initially excited about this discovery and even wanted to publish an arXiv paper directly.
However, humans were still one step ahead.
The original paper authors quickly released a v2 version, completely concluding the matter by rewriting the threshold to 1.75/L.
Sebastien still found this discovery very encouraging. Why? Didn't AI fail to defeat humans?
Because in the proof, GPT-5 Pro was trying to prove 1.5/L, not 1.75/L, which also shows that GPT-5 Pro did not directly search for the v2 version.
Additionally, the above proof is very different from the v2 proof, and it looks more like an evolution of the v1 proof.
Looking at this, the current AI capabilities are not just at the doctoral level, but often exceed it.
This discovery also led many experts to believe that the next field AI might change and influence is mathematics.
With AI's help, the boundaries of human knowledge will be expanded once again.
OpenAI's president Greg Brockman even suggested this might be a sign of AI's vitality in the mathematical field.
Moreover, this discovery is different from OpenAI's previous announcement of winning IMO and IOI gold medals.
The model that broke through this mathematical problem is the user-facing GPT-5 Pro version, not an internal reasoning model.
Sebastien stated that this conclusion was verified by himself in 25 minutes.
As a former Microsoft AI Vice President and Distinguished Scientist, his proof should be reliable, and it seems that AI has indeed practically proven this mathematical problem.
Although GPT-5's release has been mixed with praise and criticism.
However, GPT-5 Pro has truly reached, and even exceeded, the "doctoral-level" AI mentioned by Altman.
Although the problem solved this time has not yet surpassed humans, the potential for completely autonomous, self-discovered capabilities still demonstrates AI's capabilities.
This reminds me of MOSS from The Wandering Earth, an AI that is self-discovering, self-organizing, and self-programming.
Sebastien is an impressive person.
He is currently working on artificial intelligence at OpenAI.
Previously, Sebastien served as Microsoft's Vice President and Chief Scientist, working at Microsoft Research for 10 years (initially joining the theoretical research group).
Sebastien also served as an assistant professor at Princeton University for 3 years.
In the first 15 years of Sebastien's career, he mainly researched convex optimization, online algorithms, and adversarial robustness in machine learning.
He has received multiple best paper awards for these research works (including STOC2023, NeurIPS2018 and 2021 best paper awards, best student paper awards at ALT2018 and 2023 with Microsoft Research interns, COLT2016 best paper award, and COLT2009 best student paper award).
He is now more focused on understanding how intelligence emerges in large language models and how to use this understanding to improve the intelligence of large language models, potentially ultimately achieving Artificial General Intelligence (AGI).
Sebastien and others call this method "AGI physics" because he tries to reveal how different parts of AI systems work together at different scales (parameters, neurons, neuron groups, layers, data curriculum, etc.) to produce these models' surprising and unexpected behaviors.
It seems that mathematicians and scientists like Sebastien are working to try to crack the black box of large models.
Hope that while AI expands the boundaries of human cognition, humans can also unravel the secrets of large models.
References:
https://x.com/Sebastien%20Bubeck/status/1958198661139009862
This article is from the WeChat official account "New Intelligence", author: New Intelligence, editor: Ding Hui, published with authorization from 36Kr.