Compared with other zk-SNARKs, Groth16 has a relatively small proof size and fast verification time, which makes it very suitable for DeGate's requirements for efficient and secure transaction processing.
Written by: Carlos Ramos
DeGate is a decentralized transaction protocol based on zero-knowledge (ZK) technology built on Ethereum. As a ZK Rollup decentralized exchange (DEX), DeGate provides a trading experience similar to popular centralized exchanges (CEX) such as Binance or Bybit. The protocol supports multiple functions, including spot trading and grid trading, and more functions will be added continuously to ensure a smooth trading experience. DeGate is designed to make transactions fast and at low cost, providing users with more efficient and convenient transactions when acquiring various asset tokens.
In this paper, we dig into DeGate's architecture and the zero-knowledge and Groth16 techniques behind it.
DeGate's technical architecture
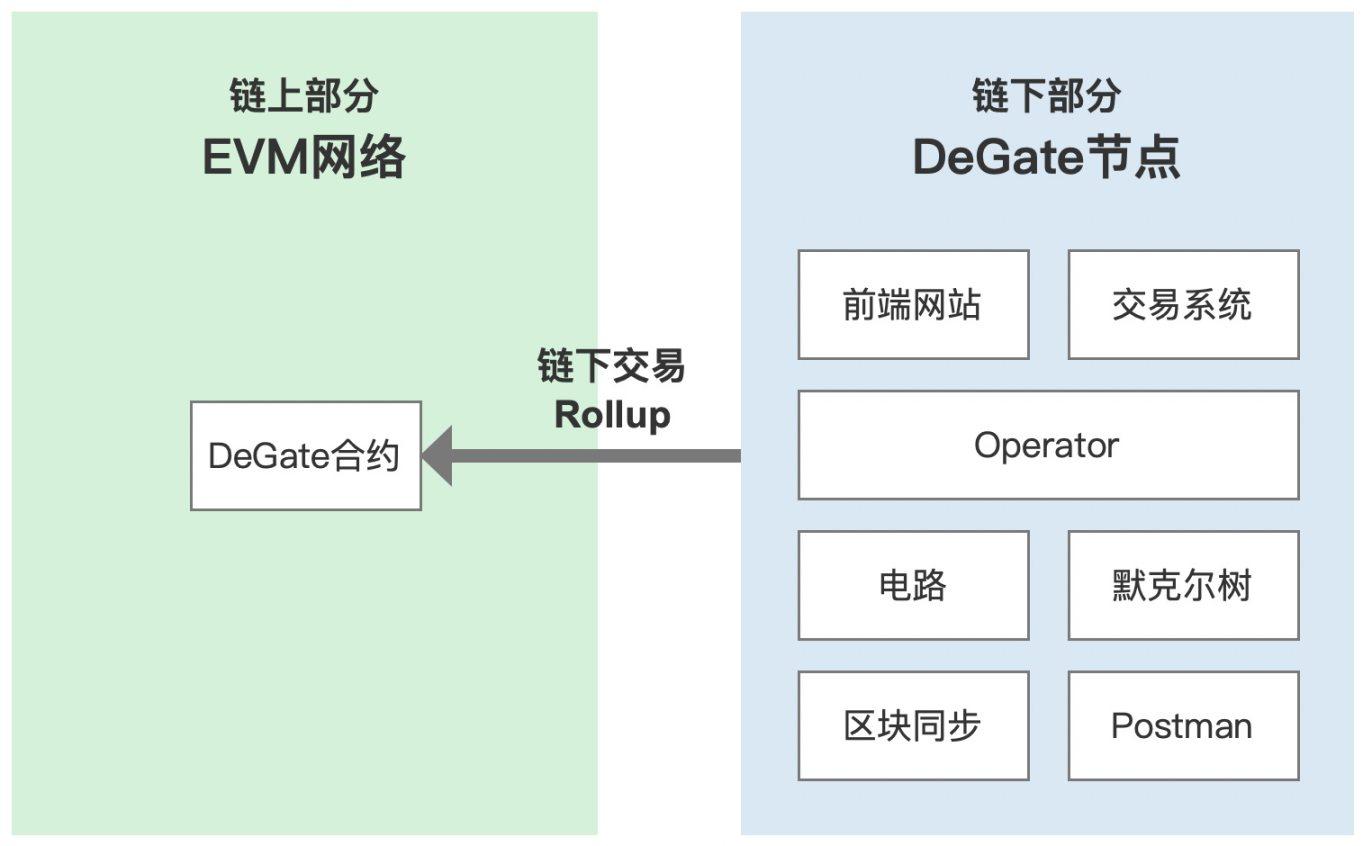
The core technology of DeGate is zero-knowledge rollup (ZK- Rollup), which contains some on-chain and off-chain components. Account and asset changes are processed off-chain and aggregated into on-chain smart contracts.
On-chain components
DeGate smart contracts are on-chain components. The smart contract is deployed on the Ethereum blockchain and is accessible to anyone who wants to interact with the exchange. This makes the transaction trustless and transparent, users have full control over their funds, and their assets can be withdrawn without relying on DeGate at all (refer to the Exodus model ). Smart contracts deployed on the EVM network store assets, verify Zero-knowledge Proof, and provide recharge and withdrawal methods.
Off-chain components
DeGate also utilizes off-chain order matching and Order-book management to reduce transaction costs and increase transaction execution speed. This is thanks to the zk-rollups technology, which allows high volumes of transactions to be processed quickly and efficiently without burdening the Ethereum network, while remaining secure and trustless.
DeGate off-chain nodes mainly include:
- Trading system: process user's orders, match orders in the Order-book, and handle events of account and asset status changes.
- Operator: Regularly process off-chain account and asset transactions, generate zkBlock, call zkp-worker, and submit proof (zkBlock data).
- zkp-worker: Describe events that require Zero-knowledge Proof, and generate Zero-knowledge Proof. Merkle tree: Store accounts, assets and orders of the DeGate protocol in a tree structure.
- Chain Synchronization: Observe and confirm all transactions that occur within the DeGate smart contract.
- Postman: Call the DeGate smart contract method on the EVM network and submit zkBlock data to the smart contract.
ZK- Rollup Technology
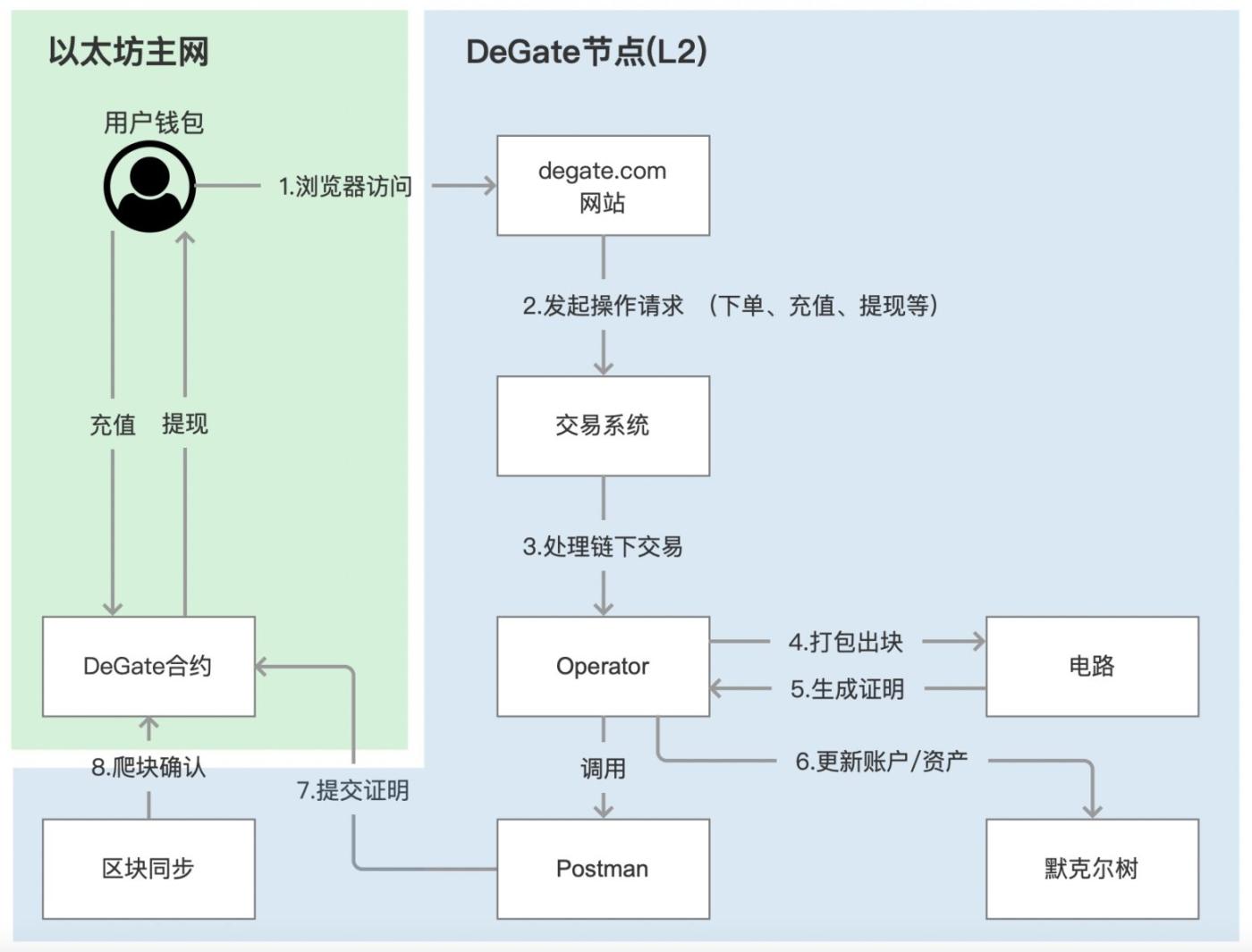
From the previous figure, we can see that DeGate has a main component named DeGate Node L2, and the Rollup process can be summarized into the following three steps:
- User signing request can be done through DeGate using asset private key (PK) or user wallet PK (transfer, deposit).
- Nodes verify and process user requests, package off-chain transactions into blocks in batches, and call circuits to generate Zero-knowledge Proof.
- The node sends the proof result to the smart contract on the chain for verification, completes ZK- Rollup and realizes data availability.
data availability
DeGate's ZK- Rollup is guaranteed by two key factors: proof generation and proof verification. In the DeGate protocol, proof generation is done by nodes through off-chain circuit programs. Relayers collect a large number of transactions to generate SNARK proofs. A SNARK proof is a hash-like content that represents a set of changes to the DeGate state. In order to achieve and prove the decentralized trust of the blockchain system, DeGate uses open source smart contracts and fixed verification keys for verification.
circuit program
About the circuit: The circuit of the Zero-knowledge Proof is a logic circuit composed of some logic gates. Any computation can be described as an arithmetic circuit. Based on this premise, complex logic operations can be broken down and described by simple addition and multiplication gates.
Zero-knowledge Proof(Zero Knowledge Proof) is a protocol that enables one party (the prover) to convince another party (the verifier) that a statement is true without revealing any information about the statement. A non-interactive Zero-knowledge Proof(NIZK) is a specific type of Zero-knowledge Proof in which the prover can generate the proof without interaction with the verifier. NIZK protocols are well suited for Ethereum applications as they allow smart contracts to act as validators. This way, anyone can generate a proof and send it to a smart contract as part of a transaction, and the smart contract can perform certain actions based on the validity of the proof. In this context, the most popular NIZK is zk-SNARK (Zero-Knowledge Succinct Non-Interactive Proof of Knowledge), which is a set of non-interactive zero-knowledge protocols with succinct proof size and sublinear verification time. The importance of these protocols is reflected in two aspects: on the one hand, they help to increase the degree of privacy protection, and on the other hand, they are a possible solution to the scalability problem, so they are very suitable for DeGate's architecture.
Like most Zero-knowledge Proof(ZKPs), zk-SNARKs allow proving computational statements. For example, the fact that knowledge of a private key associated with a particular public key, correct computation of a transaction, or knowledge of the preimage of a particular hash can be proven. Importantly, these actions can be made without divulging any information about these statements. In other words, do not reveal any information about private keys, transaction details, or preimage values. More specifically, zk-SNARKs allow proving any computational statement that can be simulated by an arithmetic circuit, such circuits are often referred to as zk-SNARK circuits. It is worth mentioning that most implementations of zk-SNARK protocols (such as Pinnochio, GGPR13, and Groth16) use elliptic curve cryptography.
Introducing Groth16 in detail
Groth16 is a Zero-knowledge Proof system implemented using elliptic curves, enabling efficient verification of computations involving arithmetic circuits. The construction is based on the following components:
- The bilinear pairing e between the two sets of points of G1 and G2: G1 x G2 -> GT, G1, G2 is a collection of some points on the relevant elliptic curve, and the size of the two point sets is r; GT is the corresponding finite field The multiplicative group of .
- A Common Reference String (CRS), which is a set of common parameters generated ahead of time and used during proof generation and verification.
- Describe the circuit C(x) whose computation is to be proven, where x is a vector of inputs to the circuit. The Groth16 construction consists of three phases: key generation, proof generation, and verification.
Groth16 construction involves several mathematical formulas and concepts, including elliptic curves, bilinear pairing functions, and Zero-knowledge Proof.
Groth16: Trusted Setup
In Groth16, the trusted setup process involves generating a Common Reference String (CRS) that is used in the proof generation and verification process. The CRS is a set of public parameters that are generated in advance and distributed to all interested parties. The process involves generating random values that are used to create the public parameters of the CRS in a way that ensures they cannot be predicted or manipulated. Private values used to generate public parameters are then destroyed to prevent them from being used to compromise the security of the system. The trusted setup process is critical to ensuring the security and integrity of the system.
Groth16: QAP and FFT
In Groth16, the proof generation process involves creating a Quadratic Arithmetic Program (QAP) that represents the computation to be proved. The QAP is then transformed using a Fast Fourier Transform (FFT) algorithm to create a compact representation of the computation that can be used in the proof.
QAP represents the computation to be proven as a set of quadratic equations, where the variables are the inputs and intermediate values of the computation. The QAP is then transformed using the FFT algorithm to create a polynomial commitment representing the computation, expressing the computation in compact form. This polynomial commitment is then used to prove the correctness of the verification computation.
The FFT algorithm used in Groth16 is based on the Cooley-Tukey algorithm, a widely used algorithm for computing the discrete Fourier transform (DFT) of a sequence. The Cooley-Tukey algorithm is used to perform an FFT on the QAP, converting it into a polynomial commitment much smaller than the original QAP.
Using QAP and FFT in Groth16 enables Zero-knowledge Proof for efficient generation and verification of computations involving arithmetic circuits. Using FFT reduces the size of the proof, making computation and verification more efficient, while using QAP allows a more natural representation of the computation to be proved.
Groth16: ALT_BN128
Curve ALT_BN128 is a known elliptic curve. A precompiled contract for this curve has been added in Ethereum's EIP196 and EIP197, which enables more gas savings by using this curve for on-chain computation.
The ALT_BN128 curve is a popular choice for pairing-based cryptography, and the earliest supported and widely used pairing curve in Ethereum. DeGate uses it for efficient verification of transactions in the protocol. Here is a comparison of the ALT_BN128 curve with some other curves commonly used in blockchain applications:
1. secp256k1: The secp256k1 curve is widely used in blockchain applications, including Bitcoin. It is defined by the equation y^2=x^3+7(mod p), where p is 2²⁵⁶-2³²-2⁹-2⁸-2⁷-2⁶-2⁴-1, which is a 256bit large prime number. The secp256k1 curve is faster than the ALT_BN128 curve in some operations, but it is not suitable for FFT calculations, so it is not used in the zk-SNARK scheme.
2. BLS12-381: The BLS12-381 curve is another popular choice for pairing-based cryptography and is used in several blockchain applications, including Zcash. It is given by the equation y^2=x^3+4(mod p), where p=2^381-3. The BLS12-381 curve is slower than the ALT_BN128 curve for some operations, but has a higher security strength.
Groth16 and ZK block sizes in DeGate
After a lot of research and discussion, DeGate finally chose Groth16 as its zk-SNARK protocol. Groth16 is widely used by many famous projects such as Zcash, and has a rich program implementation library, making it friendly to developers. It also enables DeGate to achieve fast proof generation and low ZK- Rollup cost with high security strength.
DeGate packages off-chain transactions into zk blocks and submits them to the blockchain. The number of transactions in a zk block is determined before deployment based on the number of constraints supported by the ALT_BN128 curve and the difficulty of FFT calculations. The larger the number of transactions in a zk block, the more complex the problem and the larger the number of R1CS circuit constraints. In order to ensure efficient and secure processing of zk blocks, DeGate determined several zk block sizes with a specific number of transactions. These sizes range from 5 to 355 transactions, and different sizes correspond to different sets of PK and VK. Currently, zk blocks generated by DeGate have the following sizes: 355, 300, 250, 200, 150, 100, 50, 25, 10.
trusted settings
When the DeGate protocol is deployed to the Ethereum mainnet, both circuits and smart contracts are initialized. This process, also known as trusted setup, involves random entropy. The trusted setup of the DeGate protocol is divided into two phases:
- Refer to the Power of Tau configuration as an initial value.
- Based on the initial value, first refer to the future Bitcoin block hash, then get the random entropy provided by 5 community members, and then refer to another future Bitcoin block hash. Finally, calculate and store a Proving Key and a Verifying Key, which are stored in the circuit and smart contract respectively.
Comparison of Groth16 with other schemes
Here is how Groth16 compares to some other popular and modern zk-SNARK constructions in terms of proof size and verification time:
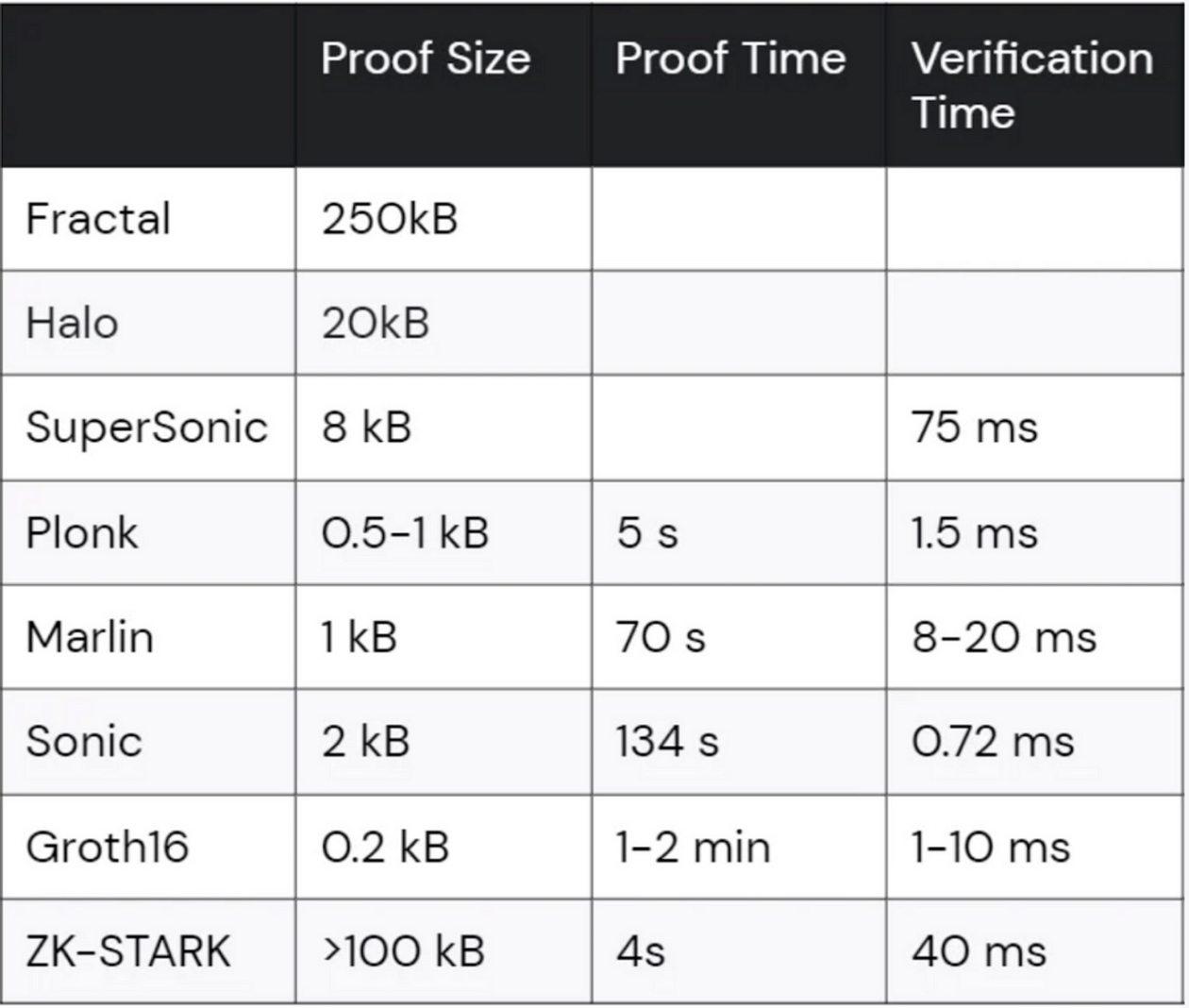
Reference source: https://www.cth.group/insights/page/zk/
GROTH VS PLONK
Although both Groth16 and PLONK are efficient zk-SNARK constructions, they have some key differences in design and implementation.
- Ease of Interpretation: Groth16 is considered more transparent than PLONK because the algorithmic principles involved are more intuitive and easier to understand and audit. PLONK involves a more complex mathematical operation and constraint process, which may make it more difficult to verify the correctness of the implementation
- The size of the proof: the proof of Groth16 is only 3 group elements, and the proof size of Plonk is generally about 2.5 times that of Groth16 under the same conditions
- Verification calculation amount: Groth16 requires more pairing calculations than PLONK; in particular, when performing batch verification of k certificates, Groth16 needs to do (k+3) pairings, while PLONK verification can be combined, always Only 2 pair calculations
- Flexibility: Groth16 adopts CRS, which requires a new trusted setup every time the circuit is changed; PLONK adopts SRS, and the circuit structure change does not require a new setup, which is more suitable for diverse tasks and needs
Overall, Groth16 is the most suitable choice when an application needs to generate multiple proofs for the same circuit (e.g. a single logic computation) and memory-related performance is critical, whereas when an application needs to handle many different circuits ( For example, business logic that can be updated quickly) and maintain high performance, PlonK is a more suitable choice.
DeGate's Zero-knowledge Proof scheme selection
DeGate chose Groth16 because of its high efficiency and safety features. Compared with other zk-SNARK constructions, Groth16 has relatively small proof size and fast verification time, which makes it very suitable for DeGate's requirements for efficient and secure transaction processing. Groth16 also has the advantage of being simple and understandable, which helps in security auditing and testing.
Therefore, for DeGate, Groth16 is currently a more suitable zk-SNARK construction, because it provides the efficiency, security and simplicity required to process transactions on the Ethereum blockchain, but the technology we choose is also For products and user services, the adoption and innovation of various advanced ZK solutions will be considered based on the following characteristics
- Efficiency: According to the DeGate product overview, the protocol is designed to handle blocks of up to 355 transactions. Groth16 is well suited for this task as it has been shown to be very efficient in pairing-based cryptography, while pairing operations are widely used in zk-SNARKs.
- Security: As mentioned earlier, Groth16 is considered very secure and has a strong track record of use in blockchain applications. This is very important for DeGate as it deals with processing financial transactions and requires a high level of security.
- Performance: The verification time of Groth16 is about 10 ms on a typical CPU, much faster than other zk-SNARK constructions. Additionally, the proof size of Groth16 is relatively small, which means less data needs to be transferred on the blockchain. This is very important for DeGate, because it helps to reduce the gas cost required to process transactions on the Ethereum blockchain; in addition, in order to further reduce the cost of verification and other processes, it can be combined with the PLONK scheme to improve the performance of the verification phase
- Scalability: In order to support more functions, realize an updatable circuit structure and fast iteration, Degate will also adopt Halo2 and other more powerful and advanced Zero-knowledge Proof schemes under diverse tasks to protect user privacy and asset security. Reduce transaction costs and meet more demands on the basis of
Summarize
This article provides an in-depth analysis of the DeGate protocol and its underlying Groth16 proof system, explaining how DeGate utilizes the Groth16 proof system to create a secure and efficient decentralized exchange platform. It focuses on the various components of DeGate's architecture, and clearly explains the Zero-knowledge Proof technology adopted by DeGate.