WHIR for Ethereum

Authors: Thomas Coratger, Giacomo Fenzi

Thank you to Justin Drake and Tom Wambsgans for the insightful and constructive feedback.

Introduction: why and how WHIR could be used for Ethereum in the future?

As Ethereum continues to scale, the demands on SNARK proof systems become increasingly sharp: proofs must be tiny, verification must be lightning-fast, and the overall system must remain simple and robust enough to be verifiable on minimal hardware — ideally something as constrained as a Raspberry Pi Pico 2, as Justin Drake recently suggested during Ethproofs call n°2. In this context, one application stands out as a proving ground for next-generation SNARKs: signature aggregation for Ethereum’s upcoming lean chain. It captures the right constraints — high throughput, strict latency, minimal verification costs, post-quantum setting — and will serve as a running example throughout this post.

These demands are driving a broader trend in proof systems: the shift from univariate to multilinear polynomial representations in proof systems. Yet working in the multilinear setting calls for new tools — especially for proximity testing, where protocols like FRI (Fast Reed-Solomon Interactive Oracle Proof of Proximity) no longer shine. This is where WHIR comes in. WHIR is a recursive, hash-based proximity testing protocol for constrained Reed–Solomon codes. It is designed to operate efficiently in both univariate and multilinear modes, making it flexible enough for a wide range of proof systems. At its core, WHIR combines two elegant ideas: a recursive folding mechanism (inspired by STIR) that compresses the domain round by round, and a lightweight sumcheck-based constraint check (à la BaseFold) that ensures algebraic correctness with minimal overhead.

The result is a tool that embodies succinctness — a key property for Ethereum — by offering small proofs (typically under 100 kilobytes with 128 bits of security conjecturing that Reed Solomon codes have mutual correlated agreement up to capacity), fast verification (typically under a millisecond to a few milliseconds, depending on the chosen hash function), and low memory usage, all while relying only on hash-based cryptographic assumptions. WHIR supports compact, low-gas SNARKs, enables efficient signature aggregation, and paves the way for recursive proofs in systems where verifier simplicity is paramount.

In the rest of this post, we will unpack how WHIR works, why it matters, and how it can help shape the future of efficient proof systems on Ethereum.

Some context on modern SNARKs

Modern SNARKs are typically built by layering a Polynomial Commitment Scheme (PCS) on top of a Polynomial Interactive Oracle Proof (PIOP). A common example is the AIR (Algebraic Intermediate Representation) model, where the prover commits to an execution trace by encoding each column of the table as a univariate polynomial. This strategy, while simple, introduces scalability bottlenecks: every column becomes a separate polynomial, leading to large proof sizes and expensive verification — often on the order of a megabyte when hundreds of columns are involved.

To overcome this, recent proof systems are shifting from univariate to multilinear representations. Instead of committing to each column separately, the entire witness is encoded as a single multilinear polynomial. This change offers several advantages: better compression, simpler constraint expression, and proof sizes that depend on the total surface of the trace, rather than its shape. Systems like Binius, Jolt, and SP1 Hypercube have embraced this trend — with SP1 being the first to demonstrate real-time proving for Ethereum blocks, using multilinear commitments.

Constraint verification in this multilinear setting can be done using the sumcheck protocol, rather than constructing and evaluating a quotient polynomial. Sumcheck offers better modularity and works seamlessly with multilinear encodings, although it comes with a performance tradeoff when using small fields. This limitation has recently been addressed by the “univariate skip” optimization, which accelerates sumcheck by folding multiple variables in the first round entirely within the base field. By doing more work upfront in a cheap, base-field domain, univariate skip reduces costly extension field evaluations in later rounds, leading to significant prover speedups without sacrificing soundness. In addition to this method, other approaches to accelerate the sumcheck protocol are being explored. A notable recent avenue of investigation is the one proposed by S. Bagad and coauthors.

Within this new stack, WHIR plays a critical role: it performs the proximity testing step, verifying that the committed multilinear function is indeed close to a valid codeword.

How does WHIR work?

This section gives an intuitive yet rigorous explanation of how WHIR operates, highlighting its core mechanisms without delving into full formal proofs. The goal is to provide a clear and accessible understanding for engineers.

Reed–Solomon code proximity testing

At a high level, WHIR is a tool to verify that a function f : \mathcal{L} \to \mathbb{F}f:L→F is “close” to a low-degree polynomial — and that this polynomial satisfies some algebraic constraint.

What is a Reed–Solomon code?

Reed–Solomon codes are sets of functions that arise from evaluating low-degree polynomials over a finite field. More precisely, suppose we choose a finite field \mathbb{F}F and a subset \mathcal{L} \subseteq \mathbb{F}L⊆F called the evaluation domain. A Reed–Solomon code of degree dd is:

In other words, these are just all possible evaluation tables of degree less than dd polynomials over the domain \mathcal{L}L. When we say a function ff is “in the code,” we mean that it is consistent with such a polynomial. When ff is “close” to the code, we mean it agrees with some codeword on most points in \mathcal{L}L — this is called proximity.

Why do we care about proximity testing?

In proof systems, a prover may send to the verifier a function ff that looks like it is evaluating a low-degree polynomial — but might not actually be. To ensure soundness, the verifier must check that ff is close to a real codeword in a Reed–Solomon code. This is the heart of a proximity test.

Multilinear view and smooth codes

WHIR works with a more structured version of RS codes. Instead of arbitrary polynomials, it uses multilinear ones — that is, polynomials where each variable appears with degree at most 1. For example, in variables x, y, zx,y,z, a multilinear polynomial could look like 3 + 2x + 5y + 7xz3+2x+5y+7xz, but not x^2x2 or y^2zy2z.

To do this, WHIR assumes that:

• The domain \mathcal{L}L is a multiplicative subgroup of \mathbb{F}^*F∗ whose size is a power of 2,
• The degree bound dd is also a power of 2, say d = 2^md=2m.

Under these conditions, any univariate polynomial \hat{f}^f of degree less than 2^m2m can be uniquely treated as a multilinear polynomial in mm variables. The evaluation of the original polynomial at a point x \in \mathcal{L}x∈L becomes equivalent to evaluating its new multilinear counterpart, which we also call \hat{f}^f, at a special vector derived from xx. This gives us the following elegant reinterpretation:

This transformation maps each point in the simple univariate domain \mathcal{L}L to a point on an mm-dimensional boolean hypercube. It allows us to apply efficient multilinear techniques (like the sumcheck protocol) while retaining the simplicity of the original code structure.

Adding constraints to the code

In many protocols, we don’t just want to check that ff is close to a polynomial — we also want to ensure that this polynomial satisfies a certain algebraic condition. For example, we might want to enforce that:

where \hat{w}^w is a fixed constraint polynomial and \sigmaσ is a known value.

To express this, WHIR uses a variant of RS codes called constrained Reed–Solomon codes. Formally, we define:

where ff is the evaluation of a multilinear polynomial \hat{f}^f on \mathcal{L}L.

This constraint ensures that ff not only comes from a polynomial — but one that satisfies a specific algebraic identity.

Folding the problem: recursive compression

To make proximity testing efficient, WHIR applies a recursive compression technique known as folding. Inspired by protocols like FRI and STIR, folding gradually reduces a large problem into a smaller, equivalent one. Each round shrinks the function’s domain and complexity while preserving its essential properties, making the final check easy for the verifier. After enough rounds, the problem becomes so small that it can be checked directly and inexpensively.

The WHIR round: combining folding and sumcheck

The core operation in this process is folding, which is best understood through an intuitive interleaved Reed-Solomon interpretation. Instead of a complex recursive formula, we can think of the domain \mathcal{L}L as being grouped into small blocks. The prover’s data within each block defines a small, local multilinear polynomial. Folding an entire block is then as simple as evaluating this local polynomial at a random challenge \alphaα from the verifier.

Mathematically, if we let p_y(X_1, \dots, X_k)py(X1,…,Xk) be the local polynomial for the block of points corresponding to a point yy in the new, smaller domain, the folding operation is just:

This single evaluation, using a random challenge vector \alpha \in \mathbb{F}^kα∈Fk, elegantly compresses the information from 2^k2k points in the original block into a single value for the new function.

WHIR powerfully enhances this idea. In a single round, it uses a kk-dimensional random challenge \alphaα to eliminate kk variables at once by applying it to two processes in parallel:

• A kk-round sumcheck reduces the main algebraic constraint to a new, simpler one.
• Folding (as local evaluation) reduces the function itself to a smaller one.

This entire round transforms the original proximity instance into a new one that is significantly smaller, where both the constraint polynomial \hat{w}^w and target \sigmaσ are updated:

This leads to a crucial efficiency gain. While we reduce the number of variables by kk (shrinking the polynomial space by a factor of 2^k2k), the evaluation domain only halves. This improves the code rate \rho = 2^m / |\mathcal{L}|ρ=2m/|L| significantly. The new rate \rho'ρ′ is given by:

The 2^{-k}2−k term comes from reducing the message space (fewer polynomial coefficients), while the 2^121 term comes from only halving the domain size. Reducing the code rate at each round is a key reason for WHIR’s low query complexity.

Soundness guarantees of folding

The folding process is carefully designed to be sound and robust, which is essential for the security of the entire proof system.

• Folding preserves a function’s distance from the code. If a function starts far from any valid codeword, it remains far after folding. Errors cannot be hidden or cancelled out by the algebraic mixing.
• In the list-decoding setting, multiple valid codewords might be close to the prover’s function. Folding is guaranteed (with high probability) to map this entire list of nearby codewords faithfully to the new, smaller problem. No spurious or false solutions are introduced during the recursion, ensuring the verifier is not misled.

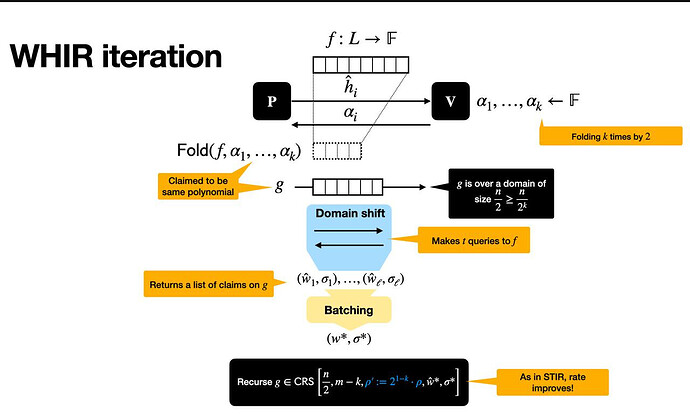
Summary of a WHIR iteration

Each WHIR iteration, illustrated in the following figure, reduces a proximity testing problem into a smaller one, while preserving soundness.

image1280×771 91.2 KB

This happens in three main phases:

Setup

We start with a function f : \mathcal{L} \to \mathbb{F}f:L→F, defined over a structured domain \mathcal{L}L (a multiplicative subgroup of size 2^m2m). The prover claims that ff comes from evaluating a multilinear polynomial \hat{f}^f, and that this polynomial satisfies a constraint like:

where \hat{w}^w is a simple constraint polynomial. This is the core statement we want to verify.

Interaction phase

The verifier sends a random challenge \alphaα, which instructs the prover to fold the function — compressing two inputs into one by hiding one variable. This produces a new function f' = \mathrm{Fold}(f, \alpha)f′=Fold(f,α), defined over a smaller domain \mathcal{L}^{(2)}L(2) and involving m - 1m−1 variables instead of mm.

To ensure that folding was done honestly, the verifier performs several checks:

• It samples a random point outside the domain and asks the prover for its evaluation, ensuring that f'f′ really comes from a low-degree polynomial.
• It samples a few values from the folded function and compares them against what ff says they should be, enforcing consistency.
• It combines all these checks (along with the constraint) into a single equation using a random linear combination, and prepares a new constraint polynomial for the next round.

Recursive claim

At the end of the round, the verifier and prover agree on a new claim: that f'f′ is close to a new polynomial \hat{f}'^f′ over a smaller domain and fewer variables, and that \hat{f}'^f′ satisfies a new constraint:

This new instance has exactly the same form as the original, just smaller. WHIR then recurses on this claim, repeating the same steps until the function is small enough to check directly.

The beauty of this approach is that each round can strip away kk variables at once, while only shrinking the domain by a factor 22, and thus reducing the rate. At the end, the verifier has high confidence that the original function ff was close to a valid codeword that satisfied the constraint — all with very little effort.

What WHIR can offer to Ethereum

What makes WHIR different is how it performs the proximity check. Instead of relying on traditional techniques like FRI, WHIR uses a recursive approach based on folding plus sumcheck, making it especially effective in the multilinear setting (where the witness is a function over \{0,1\}^m{0,1}m). This design enables several benefits particularly relevant to Ethereum and similar onchain environments.

• Extremely low query complexity. WHIR requires only a handful of queries to perform a proximity test. This means fewer Merkle openings, less data sent onchain, and ultimately much lower verification costs.

• Fast verification, often in microseconds to low milliseconds. WHIR is designed for ultra-fast verification — typically within a few hundred microseconds when using fast hash functions like Keccak or Blake3, and up to a few milliseconds when using SNARK-friendly hash functions like Poseidon2. It achieves this by combining two powerful ideas: the sumcheck protocol from BaseFold, which verifies polynomial identities with minimal overhead, and recursive folding from STIR, which compresses the problem size in each round. Together, they turn a global proximity check into a series of smaller ones that are easy to verify.

• Smaller proofs. WHIR significantly reduces proof size, especially in multilinear settings. Instead of committing to each column of the trace as a separate univariate polynomial, WHIR allows the entire witness to be represented as a single multilinear polynomial \hat{f}^f. Only one commitment is needed, and recursive folding reduces the size of the domain round-by-round. This leads to fewer commitments, fewer queries, and less encoding overhead, resulting in dramatically smaller proofs even for large computations.

• Flexible encoding. WHIR supports both univariate and multilinear encodings. This makes it compatible with a wide range of SNARK constructions — whether they use traditional univariate encodings (like PLONK or FRI-based systems), or multilinear approaches.

Applications on Ethereum

Thanks to its compact proofs and microsecond-level verification, WHIR is especially well-suited to Ethereum applications:

• Rollups. State transitions in rollups can be encoded as multilinear polynomials. WHIR helps prove these transitions compactly, with extremely fast verification for the Ethereum L1 verifier.
• Signature aggregation: With the future need for a post-quantum replacement for BLS signatures, efficiently verifying thousands of hash-based signatures is paramount. WHIR provides the cryptographic engine to compress these large collections into a single, constant-size proof with a minimal on-chain verification footprint.
• Low-gas SNARK verification: On-chain gas costs are dominated by data storage and computation. WHIR targets both by minimizing its query complexity (reducing Merkle path data) and its verifier’s computational work. While certain pre-quantum SNARKs remain highly optimized, WHIR’s performance establishes it as a leading contender for post-quantum systems where on-chain efficiency is non-negotiable, as explored in this research post.

In short, WHIR is a fast, recursive, and flexible proximity protocol that fits naturally into modern SNARK stacks. For Ethereum, it offers a path to smaller, cheaper, and faster proofs — especially in systems that already benefit from multilinear encodings.

WHIR vs. FRI: A Generational leap in proximity testing

FRI has been a cornerstone of modern proof systems, particularly STARKs. Its design uses recursive folding to efficiently test that a committed function is close to a low-degree polynomial. In the classic STARK pipeline, you first combine all your algebraic constraints into a single, high-degree “composition polynomial,” and then you run FRI on it to prove it is actually a polynomial of the expected low degree. This approach is powerful and established the viability of post-quantum proofs with polylogarithmic verifiers.

However, the landscape of SNARK design is shifting. Modern systems like Jolt, Binius, and SP1 Hypercube are moving away from this two-step “combine-then-test” model towards a more integrated, multilinear approach. In this new paradigm, proofs are built around the sumcheck protocol, a tool for verifying claims over multilinear polynomials. This is where WHIR represents a fundamental evolution.

WHIR rethinks the proximity test for this modern, sumcheck-native world. Instead of being a generic low-degree test that you run after handling constraints, WHIR integrates the constraint verification directly into its recursive process. An FRI round roughly consists of folding the domain and performing a consistency check on a random point. A WHIR round, in contrast, combines this folding with a lightweight sumcheck, which not only ensures the folding was correct but also carries the algebraic constraints of the computation forward to the next, smaller instance.

This architectural difference leads to critical performance advantages:

• Asymptotically fewer queries. This is WHIR’s biggest advantage. For a computation with 2^m2m elements, FRI’s query complexity grows linearly with mm, while WHIR’s grows logarithmically with mm. For large-scale computations, this is a dramatic improvement. In practice, it means far fewer Merkle path openings, which are a major driver of proof size and on-chain verification gas costs.

• Native multilinear and constraint support. WHIR is an IOP of proximity for constrained Reed-Solomon codes. It is built to handle the multilinear polynomials and sumcheck-based relations that define modern proof systems. While FRI can be adapted to these settings, WHIR treats them as first-class citizens, resulting in a cleaner, more efficient design.

• Exceptionally fast verification. The combination of fewer queries and a lightweight, sumcheck-based verifier logic allows WHIR to achieve verification times in the hundreds of microseconds. This makes it ideal for on-chain applications where every microsecond of verifier work translates directly to user costs and network throughput.

Signature aggregation: a concrete use case for WHIR

One of the key challenges facing Ethereum’s future consensus layer is finding a post-quantum replacement for BLS signatures. Several proposals have been explored — including lattice-based schemes and accumulation-based protocols — but many of them struggle to balance scalability, efficiency, and post-quantum security.

A particularly promising direction is to use XMSS signatures, which are hash-based and quantum-safe by design. However, XMSS signatures are large and expensive to verify individually, so aggregation becomes essential. The idea is to compress thousands of individual signatures into a single, succinct proof using a hash-based SNARK that would be then posted onchain. As described in this Ethereum Research post, such a protocol must support two operations:

• Aggregate: compress a large batch of raw signatures into one SNARK proof,
• Merge: recursively combine two existing aggregate proofs into a single proof.

The Merge operation introduces a recursive proving requirement — and this is where WHIR shines. Thanks to its folding mechanism and minimal query complexity, WHIR makes it much easier to build small and easy to verify SNARKs. Fewer queries mean fewer hash evaluations, directly reducing the cost of verifying each layer of recursion. Compared to traditional PCS constructions like FRI, WHIR enables much faster recursive proofs — a critical factor for real-time signature aggregation.

Performance today, and what’s next

A natural way to measure performance in this context is by the number of hashes (e.g., Poseidon2) that can be proven per second. Our current WHIR implementation achieves:

• 1 million Poseidon2 hashes per second on a high-end GPU (RTX 4090),
• 100,000 Poseidon2 hashes per second on a consumer-grade CPU.

Both the PCS logic (WHIR-P3) and PIOP layer (Whirlaway) are public and actively optimized. While the current bottleneck is CPU performance, ongoing efforts aim to reach parity with GPU speeds — targeting 1 million hashes per second on CPU, comparable to what systems like Plonky3 already demonstrate.

Summary and next steps

WHIR offers a compelling new approach to proximity testing, especially well-suited to the needs of Ethereum: small proof sizes, fast verification, and seamless integration with both univariate and multilinear proof systems. Its recursive folding strategy and constraint-checking mechanism via sumcheck make it an ideal fit for modern SNARK stacks, particularly in applications where efficiency and simplicity are paramount — like rollups, zkVMs, and signature aggregation for the lean chain.

In this post, we’ve focused on the WHIR protocol itself and its advantages. But WHIR is only one component of a complete SNARK. In a future post, we’ll describe how to build a full proof system around WHIR, showing how it fits into a complete pipeline for signature aggregation using hash-based cryptography.

Meanwhile, we are actively optimizing our implementation — aiming for GPU and CPU proving speeds that match or surpass today’s best systems, while keeping the protocol modular and easy to adopt. We currently maintain an open-source WHIR implementation based on Plonky3 (WHIR-P3), and we plan to upstream it directly to Plonky3 as a community-driven effort. This aligns with our vision of making WHIR a public good — open, maintained collectively, and easily integrated into other projects.

Already, several teams working on zkVMs have expressed interest in adopting WHIR, and we believe many more use cases will emerge as the Ethereum ecosystem evolves.

Our goal is to make WHIR not just a fast and elegant idea — but a practical building block for the next generation of onchain proofs.