By BitMEX Research
Source: https://blog.bitmex.com/quantum-safe-lamport-signatures/
Abstract : We introduce Lamport signatures, a quantum-safe digital signature scheme based on hash functions, invented in 1979. We use them to explain how quantum-safe signatures can be very simple, requiring no complexity or new mathematics. We argue that these hash-based signatures may be the path we should take if Bitcoin were to adopt a quantum-safe signature scheme. There is no definitive reason to believe that quantum computing poses an imminent threat to Bitcoin (not for some time to come). However, we believe that the first step in mitigating the perceived threat of quantum computing is to provide users with a quantum-safe method for spending their Bitcoin. Once such an option becomes available, adoption by ordinary users will naturally drive the next step.

- Lesslie Lamport, American mathematician and computer scientist -
Overview
"Bitcoin's exposure to quantum computing threats" has been a hot topic lately. There was even a recent conference at the Presidio Bitcoin in San Francisco dedicated to this issue. We believe that people should act as rationally as possible. We don't understand quantum computing, and we haven't seen any impressive results with quantum computing hardware yet, so there seems to be little cause for concern. However, we also understand that our ideas may be frightening to some; quantum computing could (in theory) advance very rapidly. A common concern is that Bitcoin may need to upgrade to a new, complex, and risky post-quantum cryptographic digital signature scheme. You can read about a host of trendy-sounding schemes, including HAWK , SQI , Falcon , and CRYSTALS . These new schemes may also have their own risks. What if we choose the wrong one? In 2023, there were reports that a new post-quantum cryptographic scheme, the " SIKE algorithm ," was broken by conventional, non-quantum computing. Moreover, if quantum computing advances so rapidly that almost no one understands it, who can say for sure that these schemes are truly secure?
However, if Bitcoin were to upgrade to a post-quantum digital signature scheme, there would be no need for complex, risky new technology. Recall that Bitcoin's digital signature scheme, the Elliptic Curve Digital Signature Algorithm (ECDSA), is potentially quantum-vulnerable due to its use of Shor's algorithm for rapid prime factorization. However, hash functions are very secure against quantum computing. The vulnerability of hash functions like SHA256 is that their security is quadratically degraded by Grover's algorithm , meaning that instead of having 256 bits of security, they will only have 128 bits. This seems to be largely acceptable, and if necessary, you can always use a hash function with a sufficiently long output.
In fact, there is a signature scheme that relies entirely on hash functions. For example, the Lamport signature , invented in 1979, is very simple, much simpler than the elliptic curve-based scheme used by Bitcoin. Moreover, because it relies solely on hash functions, it is quantum-safe. Therefore, if Bitcoin were to incorporate a quantum-safe signature scheme, it wouldn't need to rely on fancy new math; instead, we could simply choose a scheme based on hash functions. Bitcoin could then use hash functions for everything, including proof-of-work mining and signatures, making Bitcoin even simpler. In the remainder of this article, we'll explore the concept of Lamport signatures and how they work.
How does Lamport signature work?
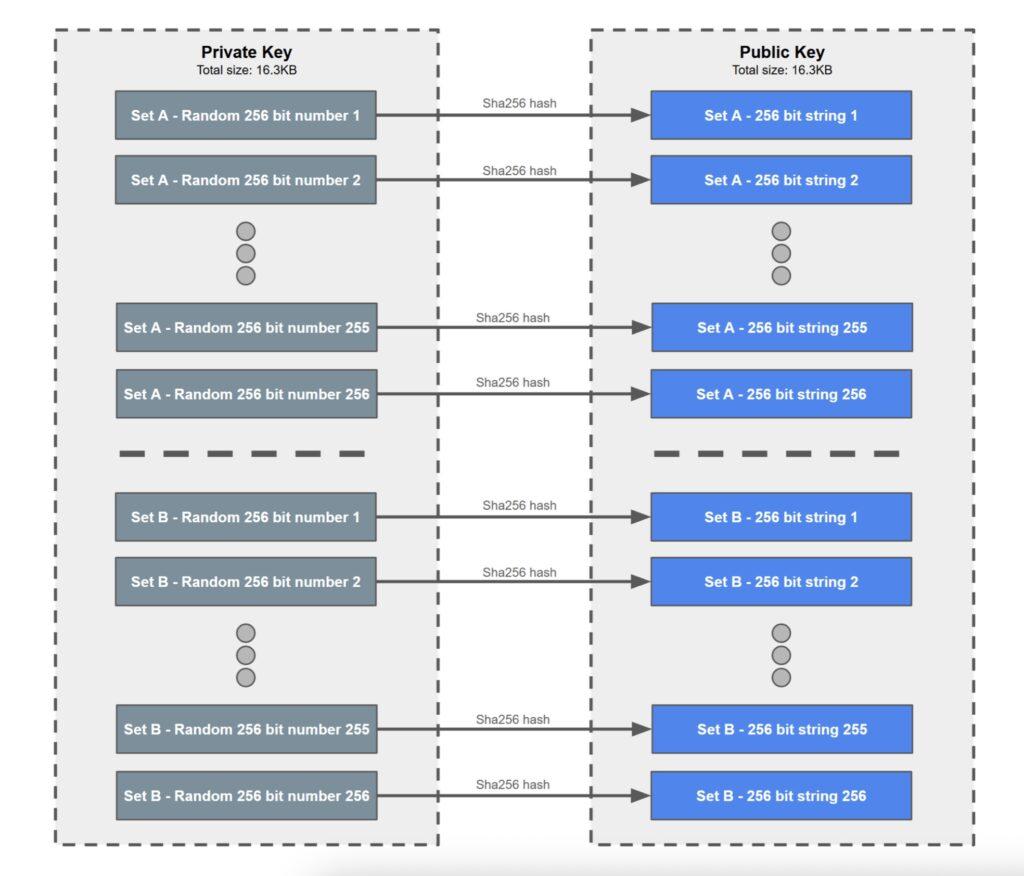
In the following examples, we assume Lamport signatures use the SHA256 hash algorithm, but almost any hash function can be used without affecting the working principle. In Lamport signatures, a private key is not a single 256-bit random number like in ECDSA signatures. Instead, it consists of two sets of random numbers, each containing 256 256-bit random numbers. In this example, we call these two sets "Set A" and "Set B." Therefore, in Lamport signatures, a private key is 2 * 256 * 256 = 131072 bits = 16.3 KB . Each of these 512 256-bit random numbers is hashed, and the resulting hash becomes the corresponding public key, resulting in a public key size 16.3 KB . A Bitcoin address can be the SHA256 hash of the concatenation of all the strings that make up the public key. The following diagram illustrates the correspondence between private and public keys.
When signing a message, the first step is to hash it, also using SHA256, and convert the output (the hash value) to binary. Each digit of this binary number determines which private key is included in the signature—0 for set A, 1 for set B. The first bit of the hash value corresponds to the first random number in the private key, the second bit to the second random number, and so on. Therefore, the signature is generated entirely by a random selection of 50% of the private key.
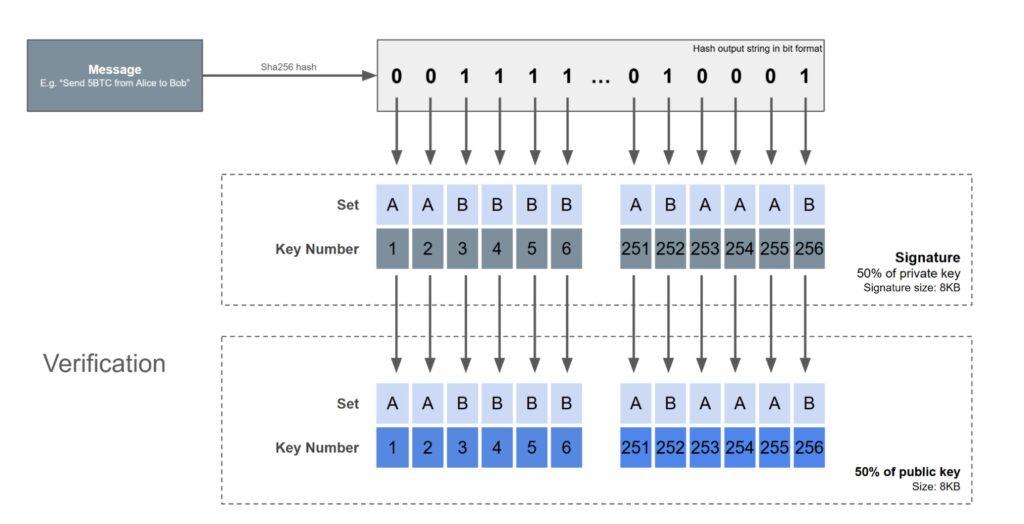
To verify this message, all the verifiers need to do is hash the message and use each bit of the binary representation of the hash value to determine which public key to use for verification. The verifier then hashes each digit in the signature to see if it matches the corresponding public key. If they match exactly, the signature is valid. The signer needs to know all the private keys, and because the hash function is random, it's impossible to predict which piece of Set A or Set B the signature will require until the message to be signed is known. Therefore, it's easy to see why this scheme is secure; the verification process is computationally straightforward.
Disposable
A key weakness of Lamport signatures is that the public/private key pair can only be used once. Once a transaction is signed and published to the blockchain, 50% of the private key is exposed. If the same public key is used again, another 50% of the remaining private key is exposed. Statistically speaking, this means that 75% of the total private key is exposed. It's easy to see that its security decreases dramatically the more times a private key is reused. This means that people may not be able to reuse addresses, which is good for privacy, but it also has some problems:
- People are used to reusing addresses
- What happens if someone sends funds to an address that has already been used?
- How to implement RBF? It can be achieved by adding an additional input and only signing this additional input, but this will also bring about the UTXO selection problem.
No flexible math
Another disadvantage is that it cannot use flexible mathematical techniques like ECDSA. For example, BIP-32 deterministic hierarchical wallets take advantage of ECDS features to allow the use of "xpub (extended public keys)"; this is not possible in a system with only hash functions.
volume
Another major issue is the sheer size of Lamport's public key and signature. A public key is 16 KB, and a signature is 8 KB, for a total of 24 KB. A Bitcoin block can only contain a few dozen transactions, while today's blocks can contain thousands. However, all quantum-safe solutions appear to share this issue to some degree.
SPHINCS+
We've just analyzed the original Lamport signature scheme for demonstration purposes, demonstrating how a signature scheme relying solely on hash functions can work and be quantum-safe. If Bitcoin were to incorporate a hash-based signature scheme, there's a much more advanced option. In 1982, Winternitz published a variant of Lamport's scheme. Winternitz's scheme split the message hash in half and mapped these two numbers to different parts of the private key, requiring more rounds of hashing. In 2011, a newer variant, XMSS , emerged, and in 2015, SPHINCS , another variant of the hash-based signature scheme, was introduced.
SPHINCS+ allows for significantly smaller signatures, and private keys can be reused multiple times. These schemes all use a Merkle tree construction, with a "global public key" at the top, resulting in a generally small signature size of just 32 bytes. If Bitcoin were to adopt a post-quantum signature scheme, these hash function signature schemes with Merkle trees could be used. Because Bitcoin already makes extensive use of Merkle trees, they are also very convenient for signatures.
Olaoluwa Osuntokun, co-founder of Lightning Labs, presented SPHINCS+ signatures at the recent Quantum Security Conference in San Francisco. In his presentation, he explained the trade-offs faced when using SPHINCS+ and how to achieve desired features based on your priorities. Adjustable parameters include the hashing cost of generating the signature, the hashing cost of verifying the signature, the number of secure reuses, and the size of the signature. Olaoluwa stated that these adjustments could ultimately reduce the signature size to 2 KB, which seems reasonable. Of course, this is still significantly larger than the current signature size on the Bitcoin chain (approximately 70 bytes).
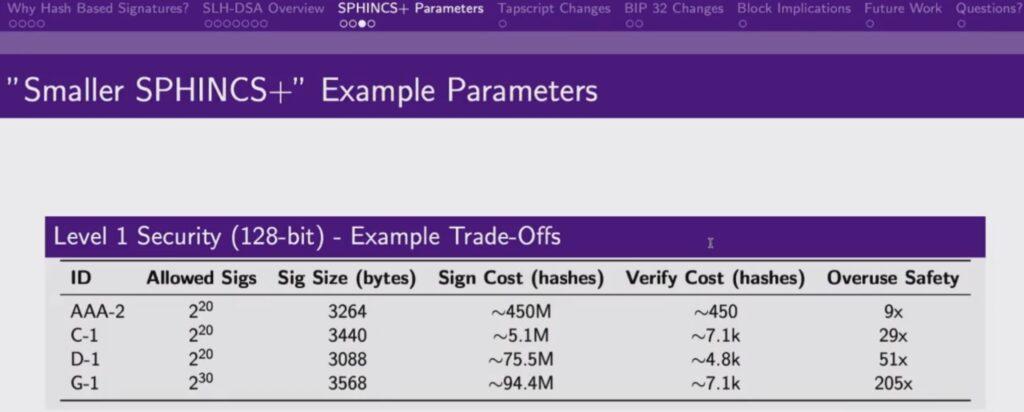
Source: https://x.com/PresidioBitcoin/status/1945877820657508650
in conclusion
We don't have a deep understanding of the quantum threat facing ECDSA, but we don't see a compelling reason to seek it. In our view, the ECDSA scheme used in Bitcoin is likely to remain secure for decades, so the rational decision might be to hold off until more concrete demonstrations of the capabilities of quantum computers emerge. However, it might be worthwhile to consider how Bitcoin could be made quantum-safe. The first step would be to create a quantum-safe method for spending Bitcoin, perhaps using a hash-based signature scheme. In our view, discussing plans to freeze vulnerable funds doesn't make any serious sense until a quantum-safe spending method is available and widely used. Only if a quantum-safe spending method is available and widely adopted would there be a point in engaging in this debate.
Of course, adding a hash-based signature scheme requires significant work. Given the significantly larger signature size, and therefore the significantly higher transaction fees, how can such a quantum-safe signature scheme gain adoption? Do we need to reinvent the wheel with block weight discounts and block size limits? Alternatively, we could measure adoption by value rather than the number of transactions/UTXOs. Perhaps these quantum-safe schemes will first be adopted by entities holding a few thousand bitcoins, such as ETF providers and Bitcoin Reserves, who rarely issue transactions. For these entities, the additional transaction fee overhead will be insignificant. Individual users can store their savings in quantum-safe outputs that require a 2KB signature to spend, while spending their daily expenses in quantum-vulnerable outputs. These daily expenses can be relatively secure by using P2WPKH outputs to avoid address reuse; P2WPKH also uses hash functions as a quantum-proof measure, so users are only at risk while their transactions are unconfirmed.
If quantum-safe signature schemes achieve widespread adoption, discussing the next steps to mitigate quantum risk will become much easier. In our view, once quantum-safe redemption options exist, ultimately, rational users will guide the path forward. If they prefer quantum-safe outputs, that's fine; that's their choice. If adoption truly becomes widespread, we can then discuss other controversial steps, such as freezing funds, changing block weight limits, quantum-safe recovery schemes like BIP-39 seed words, and whatever else people deem necessary. Let the coin holders decide.
(over)