이더리움에서 더 빠른 블록/블롭 전파
이 글에 대한 토론과 피드백을 해주신 @n1shantd , @ppopth , Ben Berger께 감사드리고, 많은 유익한 토론을 해주신 @dankrad 께도 감사드립니다.
추상적인
우리는 P2P 네트워크에서 블록과 블롭을 브로드캐스트하고 전송하는 방식을 랜덤 선형 네트워크 코딩을 사용하여 변경할 것을 제안합니다. 우리는 이론적으로 대역폭의 5%를 소비하고 현재 gossipsub 구현에서 걸리는 시간의 네트워크 홉 수의 57%(따라서 메시지당 대기 시간의 절반)로 블록을 분산할 수 있음을 보여줍니다. 우리는 계산 오버헤드에 대한 구체적인 벤치마크를 제공합니다.
소개
블록을 분배하기 위한 현재의 gossipsub 메커니즘은 대략 다음과 같이 작동합니다. 제안자는 모든 피어 중에서 D=8 피어의 랜덤 서브세트( Mesh 라고 함)를 선택하여 블록을 브로드캐스트합니다. 블록을 수신하는 각 피어는 매우 빠른 예비 검증을 수행합니다. 대부분은 서명 검증이지만 가장 중요한 것은 상태 전환이나 거래 실행을 포함하지 않는다는 것입니다. 이 빠른 검증 후 피어는 블록을 다른 D 피어에게 다시 브로드캐스트합니다. 이러한 설계에서 즉각적인 두 가지 결과가 있습니다.
- 각 홉은 최소한 다음과 같은 지연을 추가합니다. 한 피어에서 다음 피어로 전체 블록을 한 번 전송합니다(네트워크 ping 지연 시간 포함, 기본적으로 대역폭과 무관하며 대역폭에 의해 제한된 전체 블록 전송).
- 피어는 이미 전체 블록을 수신한 다른 피어에게 불필요하게 전체 블록을 브로드캐스트합니다.
우리는 브로드캐스트 레벨에서 랜덤 선형 네트워크 코딩 (RLNC)을 사용할 것을 제안합니다. 이 코딩을 사용하면 제안자는 블록을 N 개의 청크로 분할하고(예: 아래 모든 시뮬레이션의 경우 N=10 ) 전체 블록을 ~8명의 피어에게 보내는 대신 단일 청크를 ~40명의 피어에게 보냅니다(원래 청크 중 하나가 아니라 청크의 랜덤 선형 조합, 개인정보 보호 고려 사항은 아래 참조). 피어는 여전히 전체 블록 또는 N 개의 청크를 다운로드해야 하지만 다른 피어로부터 병렬로 받을 수 있습니다. 원래 블록을 구성하는 원래 청크의 랜덤 선형 조합인 N 개의 청크를 받은 후 피어는 선형 방정식 시스템을 풀어 전체 블록을 복구해야 합니다.
개념 증명 구현은 다음 숫자를 강조합니다.
- 블록을 제안하는 데는 CPU에 얽매인 26ms가 추가로 소요되며 최신 노트북(Apple M4 Pro)에서는 2ms 미만으로 완전히 병렬화될 수 있습니다.
- 각 청크를 검증하는 데 2.6ms가 걸립니다.
- 전체 블록을 디코딩하는 데 1.4ms가 걸립니다.
-
10청크와D=40사용하면, 각 노드는 현재의 가십서브보다 절반의 데이터를 전송하고 네트워크는 절반의 시간에 100KB 블록을 브로드캐스트하며 블록 크기에 따라 이점이 증가합니다.
프로토콜
네트워크 코딩에 대한 심층적인 소개를 위해 독자는 loc. cit.와이 교과서를 참조하세요. 여기서는 위에서 언급한 개념 증명 벤치마크에 대한 최소한의 구현 세부 사항을 언급합니다. 블록 전파(~110KB)의 경우 지연 시간 또는 네트워크 홉 수가 전파 시간을 지배하는 반면, 전체 DAS의 블롭과 같은 대용량 메시지의 경우 대역폭이 전파 시간을 지배합니다.
우리는 소수 특성의 유한체 \mathbb{F}_p F p 를 고려합니다. 위의 예에서 우리는 curve25519-dalek rust crate에 의해 구현된 Ristretto 스칼라 기본 필드를 선택합니다. 제안자는 불투명한 바이트 슬라이스인 블록을 가져와 \mathbb{F}_p F p 의 요소 벡터로 해석합니다. 일반적인 이더리움 블록은 약 B = 110KB B = 110KB 입니다 . 각 Ristretto 스칼라가 인코딩하는 데 32바이트보다 약간 적게 걸리므로 블록은 \mathbb{F}_p F p 의 약 B/32 = 3520 B / 32 = 3520 요소를 차지합니다. N=10 개의 청크로 나누면 각 청크는 \mathbb{F}_p^{M} F M p 의 벡터로 볼 수 있습니다. 여기서 M \sim 352 M ∼ 352 . 따라서 블록은 N N 벡터 v_i \in \mathbb{F}^M_p v i ∈ F M p , i=1,...,N i = 1 , . . . , N 으로 간주됩니다. 제안자는 D\sim 40 D ∼ 40 피어의 하위 집합을 무작위로 선택합니다. 이러한 각 피어에 추가 정보와 함께 \mathbb{F}_p^M F M p 벡터 하나를 보내 메시지를 검증하고 네트워크에서 DOS를 방지합니다. 제안자를 설명합니다.
제안자
우리는 위에 언급된 rust crate에 의해 구현된 Ristretto 타원 곡선 E E 에 대한 Pedersen 커미트먼트를 사용할 것입니다. 우리는 이미 충분한 요소 G_j \in E G j ∈ E , j = 1, ..., K j = 1 , . . . , K 의 신뢰할 수 있는 설정을 무작위로 선택했다고 가정합니다. 여기서 K \gg M K ≫ M 입니다. 우리는 \mathbb{F}_p^M F M p 에 대해 표준 기반 \{e_j\}_{j=1}^M { e j } M j = 1을 선택합니다. 따라서 각 벡터 v_i v i 는 다음과 같이 고유하게 작성할 수 있습니다.
$$ v_i = \sum_{j=1}^M a_{ij} e_j, $$
일부 스칼라 a_{ij} \in \mathbb{F}_p a i j ∈ F p 에 대해 각 벡터 v_i v i 에 대해 Pedersen 커미트먼트가 있습니다.
$$ C_i = \sum_{j=1}^M a_{ij}G_j \in E. $$
마지막으로 크기 D \sim 40 D ∼ 40 의 하위 집합에 있는 각 피어에 대해 제안자는 스칼라 b_i b i , i=1, ...,N i = 1 , . . . , N 의 균일하게 무작위적인 컬렉션을 선택하고 피어에 다음 정보를 보냅니다.
- 벡터 v = \sum_{i=1}^N b_i v_i \in \mathbb{F}_p^M v = ∑ N i = 1 b i v i ∈ F M p . 크기는 32M 32 M 바이트이고 메시지의 내용입니다.
- N N 커밋먼트 C_i C i , i=1,...,N i = 1 , . . . , N . 이는 32N 32 N 바이트입니다.
- N N 계수 b_i b i , i=1, ...,N i = 1 , . . . , N . 이는 32N 32 N 바이트입니다.
- N N 커밋 C_1 || C_2 || ... || C_N C 1 | | C 2 | | . . . | | C N 의 해시에 대한 BLS 서명은 96 96 바이트입니다.
서명된 메시지 는 위의 1~4개 요소의 모음입니다. 각 메시지에 사이드카로 전송된 64N \sim 640 64 N ∼ 640개의 추가 바이트가 있음을 알 수 있습니다.
동료 수신
피어가 이전 섹션과 같은 메시지를 수신하면 검증은 다음과 같이 진행됩니다.
- 이는 제안자의 서명과 수신 커밋먼트의 해시가 유효한지 확인합니다.
- 수신 벡터 v = \sum_{j=1}^M a_j e_j v = ∑ M j = 1 a j e j 를 쓰고 페데르센 커미트먼트 C = \sum_{j=1}^M a_j G_j C = ∑ M j = 1 a j G j 를 계산합니다.
- 수신된 계수 b_i b i 는 v = \sum_{i=1}^N b_i v_i v = ∑ N i = 1 b i v i 라는 주장입니다. 피어는 C'= \sum_{i=1}^N b_i C_i C ′ = ∑ N i = 1 b i C i 를 계산한 다음 C = C' C = C ′ 임을 확인합니다.
피어는 수신한 메시지를 추적하며, 이를 벡터 w_i w i , i = 1,...,L i = 1 , . . . , L ( L < N L < N) 이라고 합니다. 이들은 부분 공간 W \subset \mathbb{F}_p^M W ⊂ F M p 를 생성합니다. 이들이 v v 를 수신하면 먼저 이 벡터가 W W 에 있는지 확인합니다. 그렇다면 이 벡터가 이미 이전 벡터의 선형 결합이므로 버립니다. 이 프로토콜의 핵심은 이런 일이 일어날 가능성이 매우 낮다는 것입니다(위의 숫자의 경우 이런 일이 일어날 확률은 2^{-256} 2 − 256 보다 훨씬 낮습니다). 이에 대한 추론으로 노드가 N N 개의 메시지를 수신하면 메시지 w_i w i , i=1,...,N i = 1 , . . . 에서 원래 v_i v i 와 블록을 복구할 수 있다는 것을 알게 됩니다. , N .
또한 필요한 서명 검증이 단 하나뿐이고, 모든 수신 메시지는 동일한 커밋먼트 C_i C i 와 동일한 커밋먼트 세트에 대한 동일한 서명을 가지므로 피어는 첫 번째 유효한 검증의 결과를 캐시할 수 있습니다.
동료 보내기
피어는 청크를 하나 받는 즉시 다른 피어에게 청크를 보낼 수 있습니다. 노드가 w_i w i , i=1,...,L i = 1 , . . . , L 을 보유하고 있고 이전 섹션과 같이 L \leq N L ≤ N 이라고 가정합니다. 노드는 또한 수신한 스칼라 계수를 추적하므로 보유한 청크가 다음을 만족한다는 것을 알고 있습니다.
$$ w_i = \sum_{j=1}^N b_{ij} v_j \quad \forall i,$$
일부 스칼라 b_{ij} \in \mathbb{F}_p b i j ∈ F p 의 경우 내부 상태에 저장합니다. 마지막으로 노드는 수신한 첫 번째 청크를 검증할 때 검증한 제안자의 전체 커미트먼트 C_i C i 및 서명도 보관합니다.
노드가 메시지를 보내는 절차는 다음과 같습니다.
- 그들은 무작위로 L L 스칼라 \alpha_i \in \mathbb{F}_p α i ∈ F p , i=1,...,L i = 1 , . . . , L 을 선택합니다.
- 이들은 덩어리 w = \sum_{i=1}^L \alpha_i w_i w = ∑ L i = 1 α i w i 를 형성합니다.
- 이들은 다음과 같이 N N 스칼라 a_j a j , i=1,...,N i = 1 , . . . , N 을 형성합니다.
$$ a_j = \sum_{i=1}^L \alpha_i b_{ij}, \quad \forall j=1,…,N. $$
이들이 보내는 메시지는 제안자의 서명이 포함된 청크 w w , 계수 a_j a j 및 커미트먼트 C_i C i 로 구성됩니다.
벤치마크
이 프로토콜은 gossipsub과 공통적인 몇 가지 구성 요소를 가지고 있습니다. 예를 들어, 제안자는 하나의 BLS 서명을 만들어야 하고 검증자는 하나의 BLS 서명을 확인해야 합니다. 우리는 일반적인 gossipsub 작업 외에도 수행해야 하는 작업의 벤치마크를 여기에 기록합니다. 이는 프로토콜이 노드에서 갖는 CPU 오버헤드 입니다. 벤치마크는 Macbook M4 Pro 랩톱과 Intel i7-8550U CPU @ 1.80GHz에서 수행되었습니다.
이러한 벤치마크의 매개변수는 청크 수에 대해 N=10, N = 10 이고 총 블록 크기는 118.75KB로 간주되었습니다. 모든 벤치마크는 단일 스레드이며 모두 병렬화할 수 있습니다.
제안자
제안자는 N N Pedersen 약속을 이행해야 합니다. 이는 벤치마킹되었습니다.
| 타이밍 | 모델 |
|---|---|
| [25.588ms 25.646ms 25.715ms] | 사과 |
| [46.7ms 47.640ms 48.667ms] | 인텔 |
노드
수신 노드는 청크당 1 Pedersen 커미트먼트를 계산하고 제안자가 제공한 커미트먼트의 해당 선형 조합을 수행해야 합니다. 이에 대한 타이밍은 다음과 같습니다.
| 타이밍 | 모델 |
|---|---|
| [2.6817밀리초 2.6983밀리초 2.7193밀리초] | 사과 |
| [4.9479밀리초 5.1023밀리초 5.2832밀리초] | 인텔 |
새로운 청크를 보낼 때 노드는 사용 가능한 청크의 선형 조합을 수행해야 합니다. 이에 대한 타이밍은 다음과 같습니다.
| 타이밍 | 모델 |
|---|---|
| [246.67μs 247.85μs 249.46μs] | 사과 |
| [616.97μs 627.94μs 640.59μs] | 인텔 |
N N 청크를 수신한 후 전체 블록을 디코딩할 때 노드는 선형 방정식 시스템을 풀어야 합니다. 타이밍은 다음과 같습니다.
| 타이밍 | 모델 |
|---|---|
| [2.5280밀리초 2.5328밀리초 2.5382밀리초] | 사과 |
| [5.1208밀리초 5.1421밀리초 5.1705밀리초] | 인텔 |
전반적인 CPU 오버헤드.
Apple M4에서 Proposer의 전체 오버헤드는 단일 스레드로 26ms이고 수신 노드의 경우 단일 스레드로 29.6ms입니다. 두 프로세스 모두 완전히 병렬화 가능합니다. Proposer의 경우 각 커밋을 병렬로 계산할 수 있으며 수신 노드의 경우 노드가 다른 피어에서 청크를 병렬로 수신하기 때문에 자연스럽게 병렬 이벤트입니다. Apple M4에서 이러한 프로세스를 병렬로 실행하면 Proposer 측에서 2.6ms, 수신 피어에서 2.7ms가 발생합니다. 실제 애플리케이션의 경우 관련 네트워크 대기 시간에 비해 이러한 오버헤드를 0으로 간주하는 것이 합리적입니다.
최적화
구현되지 않은 일부 조기 최적화는 청크가 올 때 선형 시스템을 반전하는 것으로 구성되지만, 위에 인용된 개념 증명은 들어오는 계수 행렬을 Eschelon 형태로 유지합니다. 가장 중요한 것은 메시지의 임의 계수가 Ristretto 필드와 같이 큰 필드에 있을 필요가 없다는 것입니다. \mathbb{F}_{257} F 257 과 같은 작은 소수 필드로 충분합니다. 그러나 Pedersen 커밋먼트가 Ristretto 곡선에서 발생하기 때문에 더 큰 필드에서 스칼라 연산을 수행해야 합니다. 이러한 벤치마크를 구현하면 선형 조합에 대해 작은 계수를 선택하고 이러한 계수는 각 홉에서 증가합니다. 임의 계수를 올바르게 제어하고 선택함으로써 선형 시스템의 계수(따라서 블록을 보내는 데 필요한 대역폭 오버헤드)를 32바이트 대신 4바이트로 인코딩할 수 있습니다.
이러한 최적화를 수행하는 가장 간단한 방법은 q = p^r q = p r 인 작은 소수 p p 에 대해 \mathbb{F}_q F q 에 대해 정의된 타원 곡선을 작업하는 것입니다. 이런 식으로 계수는 부분 필드 \mathbb{F}_p \subset \mathbb{F}_q F p ⊂ F q 에 대해 선택될 수 있습니다.
개인 정보 보호 고려 사항 위에 링크된 PoC의 구현은 제안자를 포함한 각 노드가 선형 변환을 합성하기 위해 작은 계수를 선택한다는 것을 고려합니다. 이를 통해 작은 계수가 있는 청크를 수신하는 피어는 블록의 제안자를 인식할 수 있습니다. 위의 최적화는 Bareiss의 확장과 같은 알고리즘을 수행하여 모든 계수를 작게 유지하는 데 사용되거나 제안자가 필드 \mathbb{F}_p F p 에서 임의의 계수를 선택하도록 허용해야 합니다.
시뮬레이션
우리는 다음과 같은 몇 가지 단순화된 가정 하에 블록 전파에 대한 시뮬레이션을 수행했습니다.
- 우리는 10000개의 노드와 각 노드가 메시지를 보낼 D D 피어를 갖는 방향성 그래프로 모델링된 무작위 네트워크를 선택합니다. 이 노트에서 D D 는 메시 크기 라고 하며 3에서 80까지 큰 범위로 선택되었습니다.
- 피어는 전체 노드 집합에서 무작위로 균일하게 선택되었습니다.
- 각 연결은 X X MBps의 동일한 대역폭으로 선택되었습니다(이것은 일반적으로 Ethereum에서 X=20 X = 20 으로 가정되지만 이 숫자를 매개변수로 남겨둘 수 있음)
- 각 네트워크 홉은 L L 밀리초의 추가 상수 대기 시간을 발생시킵니다. (이것은 일반적으로 L=70 L = 70 으로 측정되지만 이 숫자를 매개변수로 남겨둘 수 있습니다.)
- 메시지 크기는 전체 크기인 B B KB로 가정합니다.
- RLNC를 사용한 시뮬레이션의 경우, 블록을 나누기 위해 N=10 N = 10 개의 청크를 사용했습니다.
- 노드가 중복으로 인해 해당 피어에게 메시지를 보냈을 때 해당 메시지를 삭제하는 경우(예: 피어가 이미 전체 블록을 가지고 있는 경우), 해당 메시지의 크기를 낭비된 대역폭 으로 기록합니다.
가십서브
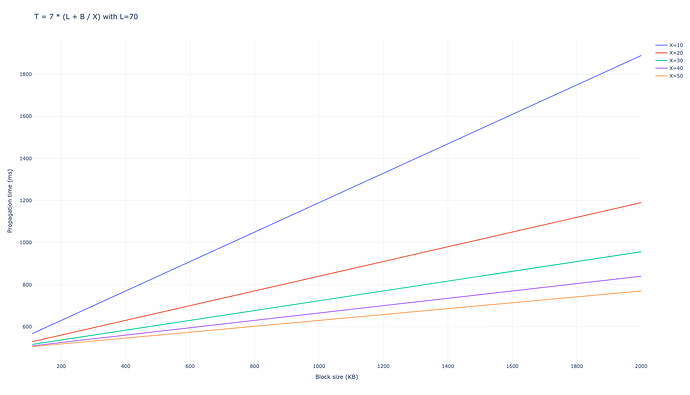
우리는 D=6 D = 6 의 메시지를 보내기 위해 피어의 수를 사용했습니다. 네트워크가 전체 블록을 네트워크의 99%로 전파하는 데 평균 7개의 홉이 걸리며, 이로 인해 총 전파 시간이 다음과 같이 됩니다.
$$ T_{\mathrm{gossipsub, D=6}} = 7 \cdot (L + B/X), $$
밀리초 단위.
D=8 D = 8 인 경우 결과는 비슷합니다.
$$ T_{\mathrm{gossipsub, D=8}} = 6 \cdot (L + B/X), $$
낭비되는 대역폭은 D=6 D = 6 의 경우 94,060 \cdot B 94 , 060 ⋅ B 이고 D=8 D = 8 의 경우 100,297 \cdot B 100 , 297 ⋅ B 입니다.
현재 이더리움 블록과 같은 B B 의 낮은 값의 경우 지연 시간이 전파에 가장 큰 영향을 미치지만, 피어 DAS 이후의 블롭 전파와 같이 더 큰 값의 경우 대역폭이 주요 요인이 됩니다.
RLNC
피어당 단일 청크
무작위 선형 네트워크 코딩을 사용하면 다양한 전략을 사용할 수 있습니다.각 노드가 크기 D D 의 메시에 있는 모든 피어에게 단일 청크만 보내는 시스템을 시뮬레이션했습니다.이렇게 하면 발생하는 지연 시간이 gossipsub에서와 동일함을 보장합니다.홉당 단일 지연 비용은 L L 밀리초입니다.이렇게 하려면 메시 크기가 청크 수인 N N 보다 상당히 커야 합니다.D_ {gossipsub} D gossipsub ( 현재 이더 리움 의 경우 8 8 ) 의 gossipsub 메시 크기의 경우 D_{RLNC} = D_{gossipsub} \cdot N D R L N C = D gossipsub ⋅ N 으로 설정 하여 노드 당 동일한 대역폭 을 사용해야 하며 현재 값으로는 80 80 이 됩니다.
이 대역폭의 절반인 훨씬 더 보수적인 값인 D=40 D = 40을 얻으면
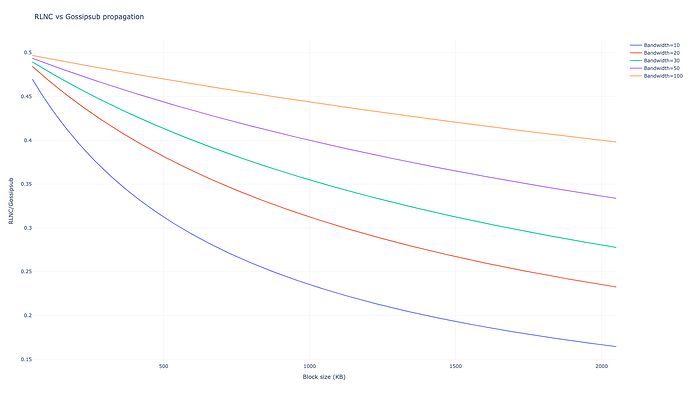
$$T_{RLNC, D=40} = 4 \cdot \left(L + \frac{B}{10 X} \right), $$
낭비된 대역폭은 29,917\cdot B 29 , 917 ⋅ B 입니다. 오늘날 D=80 D = 80 으로 얻는 것과 동일한 대역폭을 가정하면 인상적인 결과를 얻습니다.
$$T_{RLNC, D=80} = 3 \cdot \left(L + \frac{B}{10 X} \right), $$
낭비된 대역폭은 28,124\cdot B 28 , 124 ⋅ B 로, 이는 gossipsub의 해당 낭비된 대역폭의 28%입니다.
차이점
노드당 전송되는 동일한 대역폭에 대해, 지연 시간을 두 부분으로 나누는 것(홉이 3개 대 6개)과 블록을 더 빠르게 전파하여 단위 시간당 대역폭의 1/10을 소모하는 것 모두에서 전파 시간이 다르다는 것을 알 수 있습니다. 또한 불필요한 메시지로 인한 낭비 대역폭은 가십서브 낭비 메시지의 28%로 줄어듭니다. 전파 시간과 낭비 대역폭에 대한 결과는 비슷하지만 노드당 전송되는 대역폭은 절반으로 줄어듭니다.
더 낮은 블록 크기 끝에서 지연이 지배적이며 gossipsub의 3홉 대 6홉이 가장 큰 차이를 만들고, 더 높은 블록 크기 끝에서 대역폭 성능이 지배적입니다. 훨씬 더 큰 블록 크기의 경우 RLNC의 CPU 오버헤드가 악화되지만 전송 시간의 규모를 감안하면 이는 무시할 수 있습니다.
피어당 여러 청크
프로덕션에서 피어당 단일 청크 접근 방식에서 대역폭이 더 높은 노드는 더 많은 피어에 브로드캐스트하도록 선택할 수 있습니다.노드 수준에서는 현재 모든 피어에 간단히 브로드캐스트하여 구현할 수 있으며 노드 운영자는 구성 플래그를 통해 피어 수를 선택하기만 하면 됩니다.또 다른 접근 방식은 노드가 여러 청크를 단일 피어에 순차적으로 보낼 수 있도록 하는 것입니다.이러한 시뮬레이션의 결과는 위와 정확히 동일하지만 예상대로 D D가 훨씬 낮습니다.예를 들어 D=6 D = 6 인 경우 피어당 단일 청크가 전송되는 경우 전체 블록을 브로드캐스트하지 않습니다.시뮬레이션은 전체 블록을 브로드캐스트하는 데 10홉이 필요합니다.D =10 D = 10 인 경우 홉 수가 9로 줄어듭니다.
결론, 누락 및 추가 작업
우리의 결과는 현재 라우팅 프로토콜 대신 RLNC를 사용한다면 블록 전파 시간과 노드당 대역폭 사용량이 상당히 개선될 것으로 예상된다는 것을 보여줍니다. 이러한 이점은 블록/블롭 크기가 클수록 또는 홉당 지연 비용이 짧을수록 더욱 분명해집니다. 이 프로토콜을 구현하려면 현재 아키텍처에 상당한 변경이 필요하며 완전히 새로운 pub-sub 메커니즘이 필요할 수 있습니다. 이를 정당화하기 위해 Shadow 에서 시뮬레이션하기 위해 전체 네트워킹 스택을 구현하고자 할 수 있습니다. 대안은 Peer-DAS에서 하는 것과 유사하게 Reed-Solomon 삭제 코딩 및 라우팅을 구현하는 것입니다. 위의 시뮬레이션을 이 상황으로 확장하는 것은 간단할 것이지만 op. cit에는 이미 이러한 비교가 많이 포함되어 있습니다.