격자 기반 서명 집계
본 보고서는 David Nevado, 김도훈, Miha Stopar의 공동 보고서입니다.
이더리움의 지분증명(PoS)에서 BLS 서명은 여러 검증자의 증명을 하나의 컴팩트한 서명으로 통합하는 데 사용됩니다. 그러나 BLS는 양자 보안을 제공하지 않으며, 양자 이후의 미래에는 대체되어야 합니다. 유망한 방향 중 하나는 격자 기반 집계입니다. 최근 LaBRADOR를 이용한 Falcon 서명 집계(Aggregating Falcon Signatures with LaBRADOR) 와 같은 이 방식은 작은 크기와 빠른 검증 속도를 유지하면서 양자 이후 Falcon 서명을 효율적으로 집계하는 방법을 탐구합니다.
LaBRADOR는 Falcon 서명을 압축 증명(10,000개 서명의 경우 약 74KB)으로 집계하는 유망한 접근 방식을 제공하지만, 다른 포스트 양자(post-quantum) 대안도 존재합니다. 하나는 STARK를 사용하여 많은 해시 기반 서명이 유효함을 영지식(zero-knowledge)으로 증명하는 것입니다. 이러한 접근 방식은 일반적으로 더 큰 증명 크기( 10,000개 서명의 경우 약 300KB) 를 초래하지만, 검증 시간이 더 빠르다는 장점이 있습니다.
이 글을 마무리하며, LaBRADOR 방식을 최근의 해시 기반 서명 집계 방식과 비교합니다. 이 방식에서 서명은 Poseidon2로 인스턴스화되고, 집계는 머클 트리 기반 다항식 커미트먼트 방식을 위해 Keccak을 사용합니다. 집계 자체는 Plonk 방식의 증명 시스템 내에서 서명 검증기를 산술 연산하는 것으로 구성됩니다.
LaBRADOR는 비교적 새로운 프로토콜이며, 구현 지원이 아직 제한적입니다. 일부 Rust 구현이 개발되고 있지만, 아직 완성되지 않았기 때문에 현재로서는 원본 C 참조 코드가 주요 옵션으로 남아 있습니다. 벤치마킹을 위해 LaBRADOR C 구현을 래핑하는 Lazer 저장소의 agg_sig.py 스크립트를 사용했습니다. 아래에서는 먼저 몇 가지 벤치마크 결과를 제시하고, Lazer 방식이 원본 논문 "LaBRADOR를 사용한 Falcon 시그니처 집계"에 설명된 방식과 어떻게 다른지 설명합니다.
성과 결과
접근하다 :
저희는 LaBRADOR 포크를 사용했는데, 여기에는 2,000개 이상의 서명 배치를 지원하기 위한 수정 사항이 포함되어 있습니다. 이러한 수정 사항은 집계 과정에서 발생하는 더 큰 중간 값을 처리하기 위해 모듈러스를 약 2^{48} 2 48 로 증가시킬 수 있도록 이루어졌습니다.
결과 :
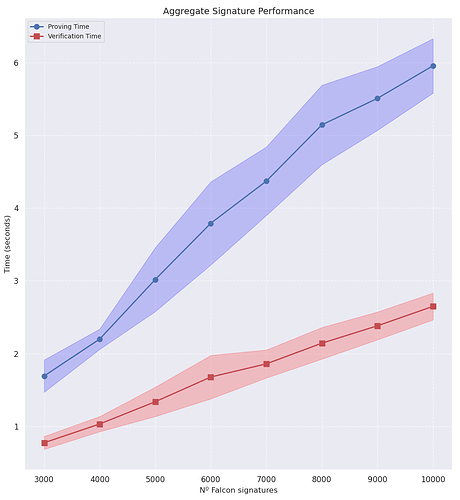
3,000개에서 10,000개까지의 Falcon-512 시그니처 배치를 집계하는 데 걸리는 시간을 측정했습니다. 벤치마크는 11th Gen Intel(R) Core(TM) i5-11400H @ 2.70GHz 프로세서에서 단일 스레드 실행으로 수행되었습니다.
| # 서명 | 증명 시간(들) | 검증 시간(초) | 증명 크기 |
|---|---|---|---|
| 3000 | 1.6921 ± 0.2220 | 0.7739 ± 0.0888 | 77.83KB |
| 4000 | 2.1991 ± 0.1403 | 1.0321 ± 0.1044 | 69.82KB |
| 5000 | 3.0182 ± 0.4394 | 1.3380 ± 0.2021 | 72.45KB |
| 6000 | 3.7914 ± 0.5716 | 1.6779 ± 0.2989 | 72.11KB |
| 7000 | 4.3709 ± 0.4716 | 1.8586 ± 0.1928 | 71.83KB |
| 8000 | 5.1447 ± 0.5469 | 2.1430 ± 0.2175 | 74.02KB |
| 9000 | 5.5085 ± 0.4382 | 2.3821 ± 0.1915 | 72.27KB |
| 10000 | 5.9565 ± 0.3750 | 2.6492 ± 0.1848 | 74.07KB |
참고 : 그래프에는 표시되지 않았지만, 이 구성은 더 큰 서명 배치를 지원합니다. 더 작은 배치(<2,000개 서명)는 모듈러스를 2^{40} 2 40 으로 줄일 수 있으므로 더 나은 성능을 달성하고, 증명/검증 시간과 증명 크기를 줄입니다.
핵심 요점 :
10k Falcon-512 서명을 LaBRADOR로 집계하면 다음과 같은 결과가 발생합니다.
- 증명 크기 74.07KB .
- 5.95초 증명 생성.
- 2.65초 증명 검증.
이러한 결과를 통해 검증 시간이 도입에 가장 큰 걸림돌로 나타났습니다. 본 연구에서는 검증의 성능을 개선하기 위해 검증 과정을 분석했습니다.
검증 세부내역
Falcon 시그니처 집계는 LaBRADOR 라이브러리에서 제공하는 압축 증명과 Dachshund 프런트엔드(Dachshund에 대한 간략한 설명은 Lazer 논문 참조)를 사용하여 수행됩니다. Dachshund 테스트에서 검증 프로세스를 프로파일링하여 병목 현상과 잠재적인 최적화 기회를 파악했습니다. 병렬화를 통해 원래 검증 시간을 개선하려고 시도했지만, 이러한 노력은 실패했습니다.
분석
팩형 증명의 검증은 1.2510 초가 걸리고 두 단계로 구성된 composite_verify_simple 에서 수행됩니다.
- simple_reduce : 간단한 문장
st와 증명p로부터 원래의 합성 문장tst파생합니다(1.1356초, 총 시간의 약 90%). - composite_verify :
ptst와 비교합니다(나머지 10%).
우리는 simple_reduce 의 우위를 고려하여 최적화에 집중했습니다.
simple_reduce 분석
48비트 모듈러스를 사용하면 상수 LIFTS = 3 . LIFTS 루프는 런타임의 77%를 소모하지만, 순차적 종속성(Fiat-Shamir 문제로 인한)으로 인해 병렬화가 불가능합니다.
| 기능 | 시간(초) | 총 런타임의 % |
|---|---|---|
init_statement() + betasq | 0.0000 | 0.00% |
reduce_simple_commit() | 0.0000 | 0.00% |
reduce_project() | 0.0451 | 3.97% |
init_constraint() | 0.0000 | 0.00% |
| 리프트 루프(3x) | 0.8800 | 77.50% |
free_constraint() + 정리 | 0.0016 | 0.14% |
simple_aggregate() | 0.1067 | 9.40% |
aggregate_sparsecnst() | 0.0969 | 8.53% |
reduce_amortize() | 0.0053 | 0.47% |
| 총 | 1.1356 | 100% |
루프 내에서 최적화 후보로 여겨지는 여러 함수를 발견했습니다. 특히 collaps_jlproj_raw() 그렇습니다.
LIFTS 루프 분석(반복당)
| 기능 | 평균 시간(초) | 총 런타임의 % |
|---|---|---|
collaps_jlproj_raw() | 0.1166 | 10.27% |
polxvec_setzero() | 0.0178 | 1.57% |
simple_collaps() | 0.0537 | 4.73% |
reduce_lift_aggregate_zqcnst | 0.1053 | 9.27% |
| 총계(반복당) | 0.2934 | 25.84% |
| 총 (3회 반복) | 0.8802 | 77.51% |
최적화 시도
LaBRADOR는 AVX-512 명령어로 고도로 최적화되었지만, 여전히 단일 스레드로 동작합니다. 병렬화를 시도했지만 다음과 같은 문제에 직면했습니다.
Fiat-Shamir 종속성 :
FS 과제의 도출은 불가피하게 순차적이며, 이로 인해 병렬화 기회가 제한됩니다.행렬 연산 :
polxvec_jlproj_collapsmat(simple_reduce의 30%)를 OpenMP로 병렬화하면 성능이 저하될 수 있습니다 . 그 이유는 다음과 같습니다.- 거짓 공유 (캐시 라인에 대한 스레드 경합)
- 메모리 대역폭 포화 상태 (AVX-512는 이미 대역폭을 최대치로 사용 중).
그러나 근본 원인을 분리하기 위해서는 추가적인 프로파일링이 필요합니다.
비교: LaBRADOR를 사용한 Lazer 및 Aggregating Falcon Signatures
처음 보면 LaBRADOR를 이용한 Falcon Signatures 집계 기술이 Lazer 기술과 상당히 다른 것처럼 보일 수 있지만, 실제로는 그렇지 않습니다.
먼저 Falcon 서명 집계가 어떻게 작동하는지 살펴보고, 두 가지 접근 방식의 차이점을 자세히 살펴보겠습니다.
팔콘 시그니처
Falcon 시그니처는 (s_1, s_2) ( s 1 , s 2 ) 로 구성되며 다음과 같습니다.
여기서 \mathbf{h} h 는 공개 키의 일부이고 \mathbf{t} t는 메시지의 해시입니다.
우리는 q q 이외의 모듈로를 사용하는 증명 체계를 통해 \mathbf{s}_1 s 1 및 \mathbf{s}_2 s 2 에 대한 지식을 증명하고 있으므로 방정식은 다음과 같이 다시 작성됩니다.
어떤 다항식 \mathbf{v} v 에 대해서.
Falcon 서명의 집계
우리는 N 개의 Falcon 서명을 집계하려고 합니다. 즉, 다음을 증명해야 합니다.
i=1,...,N인 경우 i = 1 , . . . , N .
q q 는 Falcon 체계의 모듈러스이고, 방정식은 q' > q q ′ > q 인 R_{q'} R q ′ 에서 성립해야 하지만, 링 차수는 d.d 와 같아야 합니다 . R 에 대해 등식이 성립함을 증명하기 위해 방정식에 모듈러스 q' q ′ 가 포함되어서는 안 됩니다 .
"LaBRADOR를 이용한 Falcon Signatures 집계" 논문은 LaBRADOR를 증명 시스템으로 사용합니다. 논문이 제출될 당시, 아래에 설명된 문제들로 인해 LaBRADOR는 추가적인 제약 조건 없이는 사용할 수 없었습니다. LaBRADOR 소스 코드와 Dachshund 프런트엔드는 나중에 공개되었으며, 실제로 Dachshund 프런트엔드는 LaBRADOR를 원래 그대로 사용할 수 없었던 바로 그 문제들을 직접적으로 해결합니다.
문제 1: 규범 확인
LaBRADOR에서 Johnson-Lindenstrauss 투영법을 사용한 노름 검사는 근사치이며 전체 위트니스에 한 번에 적용됩니다. 이 접근 방식은 이제 LaBRADOR 소스 코드에서 Chihuahua 프런트엔드라고 합니다. 이와 대조적으로 Dachshund 프런트엔드는 각 위트니스 벡터에 대해 개별적으로 노름 검사를 수행합니다. 위에서 언급했듯이, 서명 집계의 맥락에서 여러 개의 위트니스 벡터, 즉 \mathbf{s}_{i,1} s i , 1 과 \mathbf{s}_{i,2} s i , 2 가 있습니다.
닥스훈트가 아직 출시되지 않았기 때문에, 본 논문은 치와와 프런트엔드를 사용한다는 가정 하에 작성되었습니다. 이 프런트엔드는 전체 위트니스(즉, 모든 위트니스 벡터의 합)의 노름이 작음을 증명하며, 이는 특정 응용 분야에 적합한 접근법입니다.
존슨-린덴스트라우스 투영의 아이디어는 무작위 투영 행렬 \Pi Π를 사용하는 것입니다. 증인 \mathbf{s} s 에 대해 투영 \Pi \mathbf{s} Π s (행렬-벡터 곱셈)가 계산되고, 검증자는 투영된 벡터의 노름을 직접 계산합니다. 대략적으로 투영이 작으면 원래 벡터도 작다는 것을 나타내는 보조정리가 있습니다. 어떤 경계 b b 에 대해 |\Pi \mathbf{s}|_2 \leq \sqrt{30} b | Π s | 2 ≤ √ 30 b 이면 |\mathbf{s}|_2 \leq b | s | 2 ≤ b 입니다. 또한 \sqrt{\lambda} b \leq \frac{q}{C_1} √ λ b ≤ q C 1 이어야 합니다. 보안 수준 λ 와 상수 C_1 C 1 에 대해. 이는 집계 방식에 사용되는 모듈러스 q q 에 제약을 가합니다. 이는 본 논문에서 Falcon의 원래 모듈러스 q q 대신 더 큰 모듈러스 q' > q q ′ > q를 사용하는 이유 중 하나입니다.
그러나 서명 집계의 경우, 각 개별 위트니스 벡터(예: \mathbf{s}_{i,1} s i , 1 및 $\mathbf{s}_{i,2}$)가 작음을 증명해야 하는데, 이는 바로 Dachshund가 지원하도록 설계된 것입니다. Dachshund가 아직 출시되지 않았기 때문에, 본 논문의 저자들은 개별 위트니스 벡터에 노름 경계를 적용하기 위해 추가적인 명시적 제약 조건을 도입했습니다. 본 논문에서는 존슨-린덴스트라우스 투영을 계속 사용하지만, 모듈로 랩어라운드를 방지하기 위한 다른 목적으로 사용됩니다. 아래에서 명시적 노름 제약 조건과 모듈로 랩어라운드를 방지하기 위한 존슨-린덴스트라우스 투영의 사용을 요약합니다.
개별 증인 벡터 규범 제약 조건
||\mathbf{s}_{i,1}||^2_2 + ||\mathbf{s}_{i,2}||^2_2 \leq \beta^2 | | s i , 1 | | 2 2 + | | s i , 2 | | 2 2 ≤ β 2 임을 증명하는 것은 \beta^2 - ||\mathbf{s}_{i,1}||^2_2 - ||\mathbf{s}_{i,2}||^2_2 β 2 − | | s i , 1 | | 2 2 − | | s i , 2 | | 2 2가 음수가 아님을 증명하는 것과 동일합니다.
라그랑주의 4제곱 정리는 음이 아닌 모든 정수를 네 제곱의 합으로 나타낼 수 있다고 말합니다. 따라서 다음 네 개의 정수 \epsilon_{i,0}, \epsilon_{i,1}, \epsilon_{i,2}, \epsilon_{i,3} \in \mathbb{Z} ϵ i , 0 , ϵ i , 1 , ϵ i , 2 , ϵ i , 3 ∈ Z를 구할 수 있습니다.
i i 번째 서명의 값 \epsilon_{i,j} ϵ i , j 는 다항식의 계수로 증인에 추가됩니다.
다항식 \mathbf{a} = a_0 + a_1 X + ... + a_{d-1} X^{d-1}, a = a 0 + a 1 X + . . . + a d − 1 X d − 1 이 있을 때 , 다음 과 같이 노름을 계산할 수 있습니다( 공액 자기 동형 \sigma_{-1} σ − 1 및 X^d = -1 X d = − 1에 대해 ||\mathbf{a}||^2 = ct(\langle \mathbf{a}, \sigma_{-1}(\mathbf{a } ) \ rangle ) | | a | | 2 = c t ( ⟨ a , σ − 1 ( a ) ⟩ ) 라는 사실 사용 ) :
우리는 \mathbf{a}' = a_0 - a_{d-1} X - ... - a_1 X^{d-1}로 표시합니다. a ′ = a 0 − a d − 1 X − . . . − a 1 X d − 1 .
이제 우리는 규범 제약 조건을 LaBRADOR 제약 조건으로 다시 쓸 수 있습니다.
하지만 새로운 증인 요소가 올바르게 구성되었는지, 증인 요소의 계수가 q'. q ′ 주위를 감싸지 않을 정도로 작은지도 확인해야 합니다 .
다항식 \mathbf{a} a 의 j j 번째 계수가 어떤 값, 예를 들어 b라는 제약 조건을 표현하는 방법을 살펴보겠습니다. b :
각 \epsilon_i ϵ i 에 대해 \epsilon_{i,4},..., \epsilon_{i, d-1} ϵ i , 4 , . . . , ϵ i , d − 1 이 0이 되도록 제약 조건을 준비해야 합니다.
또한, 예를 들어 \mathbf{s}'_{i,1} s ′ i , 1 이 \mathbf{s}_{i,1} s i , 1 에서 올바르게 구성되었는지 확인해야 합니다.
\mathbf{s}_{i,2} s i , 2 및 \epsilon_i ϵ i 의 경우도 마찬가지입니다.
네 제곱의 합에 기반한 접근 방식과는 달리, 닥스훈트는 2진 분해 벡터를 사용하며, 이 벡터에 부울 계수를 갖는 다항식을 곱합니다. 성능에는 큰 차이가 없을 것으로 예상됩니다.
랩어라운드 방지
논문의 접근 방식에 따르면 다음 두 방정식에서 랩어라운드가 발생하지 않도록 해야 합니다.
결과적으로 첫 번째 방법이 더 제한적이라는 것이 밝혀졌습니다.
두 번째 방정식에서 다음을 얻습니다.
이것이 성립하는지 확인하기 위해 존슨-린덴스트라우스 투영법을 사용합니다.
이슈 2: 증인의 재편
Chihuahua 프런트엔드의 서명 집계 맥락에서의 또 다른 한계는 수많은 소위 가비지 다항식을 계산해야 하기 때문에 많은 증인 벡터를 처리할 때 비효율적이라는 점입니다.
증명자의 런타임과 LaBRADOR가 기본 케이스로 수렴하는 속도(즉, 증명 크기를 압축하는 데 필요한 재귀 단계 수)는 두 가지 주요 매개변수에 따라 달라집니다.
- 다중성 r r : 증인 벡터의 수
- 순위 n n : 각 증인 벡터의 다항식 수
이 논문에서는 보다 균형 잡힌 구성을 달성하기 위해 증인을 재구성하여 순위 n = N n = N 의 증인 벡터 r = O(\sqrt{N}) r = O ( √ N )을 목표로 하는 것을 제안합니다. 여기서 N N 은 서명의 수입니다.
원래 위트니스는 r = 2N r = 2 N 벡터로 구성되며(정확한 노름 제약 조건이 추가되면 더 많아짐), 각 벡터의 순위는 n = 1 n = 1입니다 . 이는 매우 불균형한 구성입니다. LaBRADOR의 재귀적 압축이 효율적이려면 r r 과 n n 의 크기가 더 가까운 것이 좋습니다. 이를 해결하기 위해 이 계획은 패딩 전략을 도입합니다. 위트니스는 n \approx N n ≈ N 과 r \approx \sqrt{N} r ≈ √ N 이 되도록 재구성되며, 필요에 따라 새로운 위트니스 벡터에 0을 채웁니다.
하지만 이 문제는 Dachshund 프런트엔드에서도 해결됩니다. Dachshund는 많은 수의 증인 벡터를 효율적으로 처리하도록 설계되었습니다.
반지 선택
또 다른 측면은 링의 선택입니다. 이 논문에서는 여러 옵션을 분석하지만 궁극적으로는 Lazer에서 사용한 것과 동일한 구성을 채택합니다. 다항식은 여러 개의 작은 소수 p_i p i를 모듈 로 곱하고(NTT 사용), 결과는 명시적 CRT 모듈로 q q를 사용하여 결합합니다. \mathbb{Z}_r[X]/(X^{64} + 1) Z r [ X ] / ( X 64 + 1 ) 에서 완전히 분할되는 작은 16비트 소수 p_i p i (2^{12} 2 12 ~ 2^{14} 2 14 사이 )를 사용하면 효율적인 몽고메리 산술이 가능합니다(자세한 내용은 Greyhound 논문 참조).
요약
서명 집계를 위한 두 가지 접근 방식( LaBRADOR를 사용한 Falcon 서명 집계 논문의 접근 방식과 Lazer 접근 방식)은 매우 유사하므로, Lazer 코드에 기반한 벤치마크가 두 가지 모두에 관련이 있다고 생각합니다.
벤치마크된 격자 기반 서명 집계 방식의 가장 매력적인 특징은 증명 크기이며, 도입에 있어 가장 큰 걸림돌은 검증 시간일 수 있습니다. 멀티스레딩 기술을 사용하면 검증 성능을 향상시킬 수 있지만, 이에 대한 추가 연구가 필요합니다. LaBRADOR 개발자들은 이미 LaBRADOR 프로토콜과 C 구현 모두에 대한 개선 작업을 진행 중이며, 이를 통해 검증 속도가 향상될 것으로 예상되지만, 현재로서는 그 효과를 정량화하기 어렵습니다.
향후 최적화를 통해 검증 시간이 개선될 수는 있지만, 검증에 몇 밀리초만 걸리는 해시 기반 방식 (아래 표 참조)과 비교할 수는 없습니다.
| 미터법 | LaBRADOR + Falcon(10000개 서명, 1개 스레드) | 해시 기반(8192개 서명, 4개 스레드) |
|---|---|---|
| 증명 크기 | 74.07KB | 1.7MB(최적화 시 ~128KB 목표) |
| 증명의 시간 | 5.95초 | 5초 |
| 검증 시간 | 2.65초 | 106밀리초 |
| PQ 보안 | 예(격자 기반) | 예(해시 기반: Poseidon2 서명, PCS 머클라이제이션의 Keccak) |
| 병렬화 | 탐험할 것 | 매우 좋음 - 4개의 스레드 사용; 4개까지는 거의 선형적으로 확장되고 4개 이상은 비선형적으로 확장되지만 그 이상은 효과적으로 확장됩니다. |
결론적으로, LaBRADOR 방식은 Falcon 서명 집계 시 발생하는 특정 제약 조건에 매우 적합한 것으로 보입니다. 검증 시간을 단축하기 위해 Dory 와 유사한 위임 기법을 모색하는 것이 유망한 방향이 될 수 있습니다. 이러한 프로토콜은 검증자의 복잡성을 줄여주며, 특히 증명의 규모가 크지만 검증자의 리소스가 제한된 상황에서 매우 유용합니다.