1차원 및 2차원에서 보안 DAS 재검토

저자: Benedikt ( @b-wagn ), Francesco ( @fradamt )

모든 코드는 노트북 에서 확인할 수 있습니다 .

I. 서론

Fusaka 업그레이드를 통해 이더리움은 PeerDAS 라는 데이터 가용성 샘플링(DAS) 메커니즘을 도입합니다. 기본 데이터 단위인 블롭 (blob)은 리드-솔로몬 코드를 사용하여 수평으로 확장되고 행렬의 행으로 배열됩니다. 샘플은 열로 구성됩니다.

이미지 2752×736 133KB

열은 네트워크의 전송 단위 이기도 하며, 현재 열보다 작은 것은 교환할 수 없습니다. 이로 인해 PeerDAS 초기 버전에는 두 가지 기능이 부족합니다.

• 부분적 재구성 : 데이터의 일부만 재구성하고 다시 시딩하여 재구성에 기여할 수 있는 기능입니다. 예를 들어, 전체 행렬 대신 한 행(또는 몇 행)만 재구성하고 다시 시딩하는 기능입니다.
• 완전한 메모리풀 호환성 : 트랜잭션은 블롭/행과 함께 제공되며, 종종 메모리풀에 미리 분산됩니다. 하지만 블롭이 하나만 누락되어도 노드가 열을 생성할 수 없으므로, 다른 모든 메모리풀 블롭은 쓸모없게 됩니다.

이러한 한계를 해결하기 위해 셀 수준 메시징이 프로토콜의 차기 버전 후보로 강력히 검토되었습니다(예: 여기 참조). 셀 수준 메시징은 2차원 DAS 구조 의 핵심 구성 요소이기도 하므로, 다음과 같은 사항에 대한 의문이 제기됩니다.

• 셀 수준 메시징을 통해 1D PeerDAS를 향상시키거나
• 2D 구조로 전환합니다.

또는 적어도 이 전환이 후속 반복으로 이어질지 여부에 대해서는 의문이 있습니다. 이 글에서는 두 접근 방식 모두 대역폭 소비를 최소화하면서 동일한 수준의 보안을 제공한다는 가정 하에 두 접근 방식의 효율성을 비교합니다.

면책 조항: "암호화 계층", 즉 사용되는 KZG 커밋의 보안 속성은 완전히 무시합니다. 이 계층은 여기 와 여기에서 광범위하게 연구되었습니다. 저희는 샘플링 프로세스와 관련된 통계적 보안 속성에 중점을 두고 암호화 계층을 이상적인 것으로 간주합니다.

배경: 데이터 가용성 샘플링

먼저, 데이터 가용성 샘플링(DAS)의 핵심 아이디어를 추상적으로 회상해 보겠습니다.

DAS에서 제안자는 데이터를 보유하고 이를 네트워크 전체에 배포하려고 합니다. 클라이언트(전체 노드 또는 검증자)는 데이터를 완전히 다운로드하지 않고도 해당 데이터가 실제로 사용 가능한지 검증하는 것을 목표로 합니다.

이를 달성하기 위해 제안자는 삭제 코드(erasure code)를 사용하여 데이터를 확장합니다. 각 클라이언트는 결과 코드워드의 k k 개의 임의 심볼을 다운로드하고, 모든 클라이언트가 다운로드하는 간결한 암호화 약속(succint cryptographic commitment)과 비교하여 확인합니다. DAS 환경에서 이러한 심볼은 샘플(sample) 또는 쿼리( query) 라고도 합니다. 클라이언트는 모든 k k 개의 쿼리가 성공적으로 검증된 경우에만 데이터를 수락합니다(예: 포크 선택에 해당 블록을 포함).

DAS 보안(잠재적으로 악의적인 제안자에 대한)의 핵심적인 직관은 다음과 같습니다.

• 암호화된 약속은 제안자가 유효한 코드워드를 약속한다는 것을 보장합니다( 여기서 코드 바인딩 의 개념을 참조하세요).
• 충분한 수의 클라이언트가 수락하면 삭제 코드의 속성 덕분에 이들의 집합적 쿼리를 통해 전체 데이터를 재구성할 수 있습니다.

이 글은 두 번째 요점에 초점을 맞춥니다. 재건은 실제로 어떻게 이루어지는가? 클라이언트 수는 얼마나 충분 할까? 그리고 매개변수 k k 는 어떻게 설정해야 할까?

먼저 첫 번째 질문부터 다루고, 부분 재건이 무엇을 의미하는지 설명하겠습니다. 그런 다음 보안에 초점을 맞추겠습니다.

배경: 부분 재건

DAS의 핵심 질문 중 하나는 " 누가 언제 데이터를 재구성할 수 있는가?"입니다. 네트워크에서 충분한 샘플을 다운로드하여 삭제 코드로 인코딩된 전체 데이터를 재구성할 수 있는 전능한 "슈퍼노드"가 있다고 가정해 보겠습니다. 이 경우, 악의적인 제안자가 숨겼을 가능성이 있는 몇 개의 코드 심볼만 누락된 경우, 이 슈퍼노드는 누락된 부분을 다시 계산하여 네트워크에 다시 추가할 수 있습니다(즉 , 재시딩 ). 결국 이러한 심볼은 전파되고 모든 클라이언트가 이를 수락합니다.

이러한 설정은 강력한 슈퍼노드에 의존하는 것에 대한 우려를 불러일으키며, 이는 중앙집중화 요인이 될 수 있습니다. 실제로, 최소 재구성 임계값을 가진 삭제 코드, 즉 리드-솔로몬 과 같은 소위 MDS 코드를 사용하더라도, 슈퍼노드는 재구성하기 전에 전체 원본 데이터만큼의 샘플을 다운로드해야 합니다.

바로 이 지점에서 부분 재구성 이라는 개념이 등장합니다. 전체 재구성에 필요한 샘플 수보다 훨씬 적은 수의 샘플을 사용하여 데이터의 작고 국소적인 부분들을 복구할 수 있다면, 코드가 부분 재구성을 허용한다고 합니다. 거의 모든 부분을 수집하기 위해 슈퍼노드가 필요한 대신, 여러 개의 작은 노드들이 데이터의 일부를 독립적으로 재구성할 수 있습니다. 이러한 방식으로 부분 재구성은 재구성 작업을 여러 참여자에게 분산시켜 중앙 집중식 슈퍼노드에 대한 의존도를 줄일 수 있습니다.

더 강력한 노드에 대한 의존도를 줄임으로써 네트워크의 견고성을 강화하는 것 외에도, 재구성에 필요한 CPU 부하 와 재구성된 데이터를 다시 시딩하는 데 필요한 대역폭 부하를 분산하는 것도 성능 향상으로 볼 수 있습니다. 현재 재구성은 중요 경로에서 데이터 전파에 도움이 되지 않을 가능성이 높으며, 이는 삭제 코딩을 사용하는 또 다른 이점이 될 수 있습니다. 모든 증명을 포함하여 단일 블롭을 재구성하는 데 약 100ms가 걸리기 때문입니다. 이 부하를 각각 하나 또는 몇 개의 블롭만 담당하는 여러 노드에 분산함으로써, 삭제 코딩은 보안 보장 이상의 효과를 제공할 수 있습니다.

배경: 하위 집합 건전성

이 글에서는 다양한 인코딩 방식(1D vs. 2D)의 효율성을 비교하고자 합니다. 단, 모든 인코딩 방식이 동일한 수준의 보안을 제공한다는 가정 하에 비교합니다. 이러한 비교를 의미 있게 만들기 위해서는 먼저 DAS 환경에서 "보안"이 무엇을 의미하는지 명확하게 이해해야 합니다.

우리가 고려하는 보안 개념은 부분집합 건전성(subset soundness) 으로, 적응형 공격자(adaptive adversary)를 고려합니다. 이 개념은 DAS 기초 논문 의 정의 2 로 공식적으로 소개되었으며, PeerDAS의 보안 논리를 뒷받침합니다.

직관적으로, 부분집합 건전성은 n n 개의 클라이언트/노드로 구성된 대규모 집합에서 생성된 쿼리를 관찰하는 강력한 공격자를 모델링합니다. 공격자는 어떤 심볼을 공개하고 어떤 심볼을 공개하지 않을지 적응적으로 결정하여 각 노드가 보는 관점을 효과적으로 조작할 수 있습니다. 공격자는 또한 노드의 일부(예: 고정된 ϵ > 0 ϵ > 0 에 대해 ϵ n ≤ n ) 를 선택하여 데이터가 완전히 사용 가능하다고 믿도록 속이는 것을 목표로 합니다. 특히, 이러한 선택은 노드가 생성한 쿼리에 따라 달라질 수 있습니다. 공격자가 이 게임에서 이길 확률 p p , 즉

• \epsilon n ϵ n 노드는 모두 허용하고
• 데이터를 완전히 사용할 수 없습니다. 즉, 질의를 통해 데이터를 재구성할 수 없습니다.

우리의 목적을 위해, p p 는 (어떤 적대자에 대해서든) 최대 2^{-30} 2 − 30 이 되기를 원합니다. 아래에서, n n , \epsilon ϵ , 그리고 인코딩 방식에 따라 노드당 쿼리 수 k k 를 설정하여 p \leq 2^{-30} p ≤ 2 − 30 이 보장되도록 하겠습니다.

\epsilon ϵ 의 영향 및 선택 :
위에서 설명한 보안 개념은 \epsilon \in (0, 1] ϵ ∈ ( 0 , 1 ] 로 매개변수화되며, 이는 적대자가 속이려 는 노드의 비율을 모델링합니다. 형식적 정의 와 간단한 암호화 축소를 통해 주어진 \epsilon ϵ (고정된 n n )에 대한 부분 집합 건전성은 더 큰 \epsilon' \geq \epsilon ϵ ′ ≥ ϵ 에 대한 부분 집합 건전성을 의미합니다 . 다시 말해, 적대자가 \epsilon ϵ - 분수의 노드를 속일 수 없다면 더 큰 분수의 \epsilon' ϵ ′ 를 속일 수 없다는 것은 확실합니다.

하지만 이것이 전체 합의 프로토콜과 어떤 관련이 있을까요? 공격자가 노드의 \epsilon ϵ 분율보다 많은 노드를 속일 수 없다고 가정해 보겠습니다. 속은 각 노드는 합의 과정에서 사실상 추가적인 악성 노드 로 동작합니다. 따라서 데이터 가용성 샘플링을 사용하면 공격자는 최대 \epsilon ϵ 분율의 추가적인 악성 노드를 확보하게 됩니다.

예를 들어, DAS가 없는 합의가 최대 <{1}/{3} < 1 / 3개의 악성 노드를 허용하는 경우 DAS가 있는 경우 시스템은 이제 최대 <{1}/{3} - \epsilon < 1 / 3 − ϵ 개의 악성 노드만 허용할 수 있습니다.

따라서 실제로는 적대자의 영향력이 무시할 수 있을 정도로 작게 하려면 \epsilon ϵ을 작게 선택해야 합니다. 예를 들어 \epsilon = 1\% ϵ = 1 % .

II. PeerDAS - 1D 구성

이 섹션에서는 Fusaka 업그레이드에 포함될 PeerDAS의 작동 방식을 설명합니다. 또한, 셀 수준 메시징을 통해 부분 재구성을 어떻게 지원하는지 설명합니다.

작동 원리

우리는 "암호화 계층"과 관련된 모든 것(예: 약속 및 개방)을 무시하고 데이터를 인코딩하는 방법과 클라이언트가 쿼리를 만드는 방법을 설명합니다.

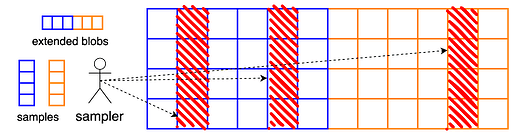
블롭은 m m 개의 셀로 구성된 집합으로, 각 셀은 f f 개의 필드 요소를 가집니다. PeerDAS의 현재 매개변수 설정에서는 셀당 f = 64 , f = 64 개의 필드 요소와 블롭당 m = 64 개의 셀 이 있습니다. 다양한 셀 크기를 고려하기 위해 fm = 4096 , f m = 4096을 상수로 두고(즉, 데이터 크기를 고정), f \in \{64,32,16,8\} f ∈ { 64 , 32 , 16 , 8 }을 변경하여 m = 4096 / f m = 4096 / f 로 설정합니다.

단일 블롭을 인코딩하려면 1/2 1/2 비율 의 리드-솔로몬 코드를 사용하여 블롭을 확장합니다 . 그 결과 2m x 2m 개의 셀, 즉 2fm = 8192 x 2fm = 8192 개의 필드 요소가 생성됩니다. PeerDAS에서는 이 인코딩 과정을 b b 개의 블롭에 독립적으로 적용하고, 확장된 블롭을 b \times 2m b × 2m 셀 행렬의 행으로 간주합니다.

이제 클라이언트는 이 행렬의 전체 열을 쿼리합니다 . 즉, b 개의 셀을 한 번에 다운로드하려고 시도합니다. 이는 "심볼" 또는 삭제 코드가 확장된 블롭 행렬의 열임을 의미합니다. 이러한 열 중 m 개 에서 전체 행렬과 데이터를 재구성할 수 있습니다.

샘플링 기능을 지원하는 구체적인 네트워킹 인프라는 열에 대한 GossipSub 주제 입니다. 즉, 특정 샘플(= 열)에 관심이 있는 노드만 참여하는 하위 네트워크입니다.

부분 재건

예상대로 현재 PeerDAS 설계는 부분 재구성을 지원하지 않습니다 . 그러나 PeerDAS처럼 여러 블롭에 독립적으로 적용할 경우 , 이러한 1차원 인코딩조차도 원칙적으로 이 기능을 지원할 수 있습니다. 실제로 셀과 같이 열보다 작은 수직 단위를 사용하면 전체 행렬의 일부(예: 개별 행 또는 행 그룹)만 재구성하는 것이 가능합니다. 이는 두 가지 과제를 야기합니다.

1. 부분적 재시드 : 노드가 단일 행을 재구성할 때 전체 샘플(열)을 재구성하지는 않지만 여전히 재구성된 데이터를 네트워크에 다시 제공할 수 있어야 합니다.
2. 재구성에 필요한 충분한 셀 확보 : 열만 샘플링하는 경우, 재구성 능력은 전부 아니면 전무입니다. 즉, 노드가 전체 행렬을 재구성할 만큼 충분한 열을 확보하거나, 아니면 그 일부를 재구성할 수 없습니다. 다시 말해, 슈퍼노드만 재구성에 참여할 수 있습니다. 노드가 전체 데이터의 일부만 다운로드하면서도 재구성에 참여할 수 있도록 하고 싶습니다.

이러한 접근 방법에는 잘 알려진 방법이 있으며, 이를 통해 부분적인 재구성을 얻을 수 있습니다.

1. 셀 수준 메시징 : 노드가 전체 열이 아닌 셀을 교환할 수 있도록 하여 행을 재구성하는 노드가 최소한 참여하는 열 토픽에서 셀 단위로 다시 시드할 수 있습니다.
2. 행 토픽 : 노드가 셀 수준 메시징 기능을 갖춘 행 토픽에 참여하여 일부 행을 다운로드하려고 시도합니다. 중요한 것은 이것이 샘플링이 아니며, 획득하는 행 수에 대한 보안 문제가 없으므로 단일 행 토픽에 참여하더라도 충분합니다. 실제로 1차원 구조에서는 수직 중복성이 없으므로 행 샘플링은 무의미합니다. 행 토픽의 목적은 열 토픽의 셀이 슈퍼노드 없이도 행 토픽으로 유입되어 행 단위 재구성을 가능하게 하는 것입니다. 재구성된 셀은 행 토픽에서 모든 열 토픽으로 유입될 수 있으며, 이 경우에도 단일 노드가 모든 셀에 참여할 필요는 없습니다.

참고: 수직 중복성이 부족하므로 모든 행 토픽이 재구성 작업을 성공적으로 수행해야 합니다. 단 하나의 행 토픽이라도 재구성 작업에 실패하면(예: 해당 토픽에 국한된 네트워크 수준의 공격으로 인해) 전체 재구성이 완료될 수 없습니다.

샘플 수

이제 PeerDAS의 클라이언트당 샘플 수 k k 를 결정해 보겠습니다. 위에서 논의한 바와 같이, 공격자가 부분집합 건전성을 위반할 확률 p p 가 최대 2^{-30} 2 − 30 이 되도록 k k 를 선택하고자 합니다.

PeerDAS의 보안은 여기 와 여기에서 광범위하게 분석되었습니다. 후자의 연구는 여기 의 보안 프레임워크를 기반으로 하며, 보조정리 1과 보조정리 3을 결합하여 부분집합 건전성에 대한 구체적인 경계를 도출할 수 있습니다. 궁극적으로 이 모든 과정을 통해 부분집합 건전성에 대한 동일한 경계를 도출할 수 있습니다. 즉, 다음과 같습니다 .

p \leq \binom{n}{n\epsilon}\cdot \binom{2m}{m-1} \cdot (\frac{m-1}{2m})^{kn\epsilon} \leq \binom{n}{n\epsilon}\cdot \binom{2m}{m-1} \cdot 2^{-kn\epsilon}. p ≤ ( n n ϵ ) ⋅ ( 2 m m − 1 ) ⋅ ( m − 1 2 m ) k n ϵ ≤ ( n n ϵ ) ⋅ ( 2 m m − 1 ) ⋅ 2 − k n ϵ .

직관적으로, 첫 번째 이항식은 적대자가 속일 n\epsilon n ϵ 노드를 자유롭고 적응적으로 선택할 수 있는 능력을 설명하고, 두 번째 이항식은 적대자가 이러한 노드에서 사용할 수 있도록 m-1 m − 1개의 심볼을 선택하는 것을 설명하며, 마지막 항은 모든 샘플이 인코딩의 이 사용 가능한 부분에 포함될 확률입니다.

p \leq 2^{-30} p ≤ 2 − 30 이고 n,m,\epsilon n , m , ϵ가 주어지기를 원한다면 다음을 설정해야 합니다.

k \geq \frac{1}{n\epsilon} \left( \log_2 \binom{n}{n\epsilon} + \log_2 \binom{2m}{m-1} + 30 \right) k ≥ 1 n ϵ ( 로그 2 ( n n ϵ ) + 로그 2 ( 2 m m − 1 ) + 30 ) .

k k를 계산하는 코드는 다음과 같습니다.

 from math import comb, log2, ceil # used later from tabulate import tabulate # used later import numpy as np # used later import matplotlib.pyplot as plt # used later def min_samples_per_node ( n: int , m: int , r: int = 2 , eps: float = 0.01 ): """Finds the smallest integer k such that k samples per nodeachieve security of 30 bits for the 1D construction.Inputs:n: total number of nodesm: number of symbols in original datar: inverse coding rate (total symbols = r*m), default=2eps: fraction of nodes to be fooled (0 < eps <= 1), default=0.01Returns:Smallest integer k satisfying the bound""" neps = int (n * eps)binom_n = comb(n, neps)binom_m = comb(m*r, m- 1 )log2_binom = log2(binom_n) + log2(binom_m)k = -(log2_binom + 30 )/(n*eps*log2( 1 /r)) return ceil(k)

열은 네트워크의 전송 단위 이기도 하며, 현재 열보다 작은 것은 교환할 수 없습니다. 이로 인해 PeerDAS 초기 버전에는 두 가지 기능이 부족합니다.

• 부분적 재구성 : 데이터의 일부만 재구성하고 다시 시딩하여 재구성에 기여할 수 있는 기능입니다. 예를 들어, 전체 행렬 대신 한 행(또는 몇 행)만 재구성하고 다시 시딩하는 기능입니다.
• 완전한 메모리풀 호환성 : 트랜잭션은 블롭/행과 함께 제공되며, 종종 메모리풀에 미리 분산됩니다. 하지만 블롭이 하나만 누락되어도 노드가 열을 생성할 수 없으므로, 다른 모든 메모리풀 블롭은 쓸모없게 됩니다.

이러한 한계를 해결하기 위해 셀 수준 메시징이 프로토콜의 차기 버전 후보로 강력히 검토되었습니다(예: 여기 참조). 셀 수준 메시징은 2차원 DAS 구조 의 핵심 구성 요소이기도 하므로, 다음과 같은 사항에 대한 의문이 제기됩니다.

• 셀 수준 메시징을 통해 1D PeerDAS를 향상시키거나
• 2D 구조로 전환합니다.

또는 적어도 이 전환이 후속 반복으로 이어질지 여부에 대해서는 의문이 있습니다. 이 글에서는 두 접근 방식 모두 대역폭 소비를 최소화하면서 동일한 수준의 보안을 제공한다는 가정 하에 두 접근 방식의 효율성을 비교합니다.

면책 조항: "암호화 계층", 즉 사용되는 KZG 커밋의 보안 속성은 완전히 무시합니다. 이 계층은 여기 와 여기에서 광범위하게 연구되었습니다. 저희는 샘플링 프로세스와 관련된 통계적 보안 속성에 중점을 두고 암호화 계층을 이상적인 것으로 간주합니다.

배경: 데이터 가용성 샘플링

먼저, 데이터 가용성 샘플링(DAS)의 핵심 아이디어를 추상적으로 회상해 보겠습니다.

DAS에서 제안자는 데이터를 보유하고 이를 네트워크 전체에 배포하려고 합니다. 클라이언트(전체 노드 또는 검증자)는 데이터를 완전히 다운로드하지 않고도 해당 데이터가 실제로 사용 가능한지 검증하는 것을 목표로 합니다.

이를 달성하기 위해 제안자는 삭제 코드(erasure code)를 사용하여 데이터를 확장합니다. 각 클라이언트는 결과 코드워드의 k k 개의 임의 심볼을 다운로드하고, 모든 클라이언트가 다운로드하는 간결한 암호화 약속(succint cryptographic commitment)과 비교하여 확인합니다. DAS 환경에서 이러한 심볼은 샘플(sample) 또는 쿼리( query) 라고도 합니다. 클라이언트는 모든 k k 개의 쿼리가 성공적으로 검증된 경우에만 데이터를 수락합니다(예: 포크 선택에 해당 블록을 포함).

DAS 보안(잠재적으로 악의적인 제안자에 대한)의 핵심적인 직관은 다음과 같습니다.

• 암호화된 약속은 제안자가 유효한 코드워드를 약속한다는 것을 보장합니다( 여기서 코드 바인딩 의 개념을 참조하세요).
• 충분한 수의 클라이언트가 수락하면 삭제 코드의 속성 덕분에 이들의 집합적 쿼리를 통해 전체 데이터를 재구성할 수 있습니다.

이 글은 두 번째 요점에 초점을 맞춥니다. 재건은 실제로 어떻게 이루어지는가? 클라이언트 수는 얼마나 충분 할까? 그리고 매개변수 k k 는 어떻게 설정해야 할까?

먼저 첫 번째 질문부터 다루고, 부분 재건이 무엇을 의미하는지 설명하겠습니다. 그런 다음 보안에 초점을 맞추겠습니다.

배경: 부분 재건

DAS의 핵심 질문 중 하나는 " 누가 언제 데이터를 재구성할 수 있는가?"입니다. 네트워크에서 충분한 샘플을 다운로드하여 삭제 코드로 인코딩된 전체 데이터를 재구성할 수 있는 전능한 "슈퍼노드"가 있다고 가정해 보겠습니다. 이 경우, 악의적인 제안자가 숨겼을 가능성이 있는 몇 개의 코드 심볼만 누락된 경우, 이 슈퍼노드는 누락된 부분을 다시 계산하여 네트워크에 다시 추가할 수 있습니다(즉 , 재시딩 ). 결국 이러한 심볼은 전파되고 모든 클라이언트가 이를 수락합니다.

이러한 설정은 강력한 슈퍼노드에 의존하는 것에 대한 우려를 불러일으키며, 이는 중앙집중화 요인이 될 수 있습니다. 실제로, 최소 재구성 임계값을 가진 삭제 코드, 즉 리드-솔로몬 과 같은 소위 MDS 코드를 사용하더라도, 슈퍼노드는 재구성하기 전에 전체 원본 데이터만큼의 샘플을 다운로드해야 합니다.

바로 이 지점에서 부분 재구성 이라는 개념이 등장합니다. 전체 재구성에 필요한 샘플 수보다 훨씬 적은 수의 샘플을 사용하여 데이터의 작고 국소적인 부분들을 복구할 수 있다면, 코드가 부분 재구성을 허용한다고 합니다. 거의 모든 부분을 수집하기 위해 슈퍼노드가 필요한 대신, 여러 개의 작은 노드들이 데이터의 일부를 독립적으로 재구성할 수 있습니다. 이러한 방식으로 부분 재구성은 재구성 작업을 여러 참여자에게 분산시켜 중앙 집중식 슈퍼노드에 대한 의존도를 줄일 수 있습니다.

더 강력한 노드에 대한 의존도를 줄임으로써 네트워크의 견고성을 강화하는 것 외에도, 재구성에 필요한 CPU 부하 와 재구성된 데이터를 다시 시딩하는 데 필요한 대역폭 부하를 분산하는 것도 성능 향상으로 볼 수 있습니다. 현재 재구성은 중요 경로에서 데이터 전파에 도움이 되지 않을 가능성이 높으며, 이는 삭제 코딩을 사용하는 또 다른 이점이 될 수 있습니다. 모든 증명을 포함하여 단일 블롭을 재구성하는 데 약 100ms가 걸리기 때문입니다. 이 부하를 각각 하나 또는 몇 개의 블롭만 담당하는 여러 노드에 분산함으로써, 삭제 코딩은 보안 보장 이상의 효과를 제공할 수 있습니다.

배경: 하위 집합 건전성

이 글에서는 다양한 인코딩 방식(1D vs. 2D)의 효율성을 비교하고자 합니다. 단, 모든 인코딩 방식이 동일한 수준의 보안을 제공한다는 가정 하에 비교합니다. 이러한 비교를 의미 있게 만들기 위해서는 먼저 DAS 환경에서 "보안"이 무엇을 의미하는지 명확하게 이해해야 합니다.

우리가 고려하는 보안 개념은 부분집합 건전성(subset soundness) 으로, 적응형 공격자(adaptive adversary)를 고려합니다. 이 개념은 DAS 기초 논문 의 정의 2 로 공식적으로 소개되었으며, PeerDAS의 보안 논리를 뒷받침합니다.

직관적으로, 부분집합 건전성은 n n 개의 클라이언트/노드로 구성된 대규모 집합에서 생성된 쿼리를 관찰하는 강력한 공격자를 모델링합니다. 공격자는 어떤 심볼을 공개하고 어떤 심볼을 공개하지 않을지 적응적으로 결정하여 각 노드가 보는 관점을 효과적으로 조작할 수 있습니다. 공격자는 또한 노드의 일부(예: 고정된 ϵ > 0 ϵ > 0 에 대해 ϵ n ≤ n ) 를 선택하여 데이터가 완전히 사용 가능하다고 믿도록 속이는 것을 목표로 합니다. 특히, 이러한 선택은 노드가 생성한 쿼리에 따라 달라질 수 있습니다. 공격자가 이 게임에서 이길 확률 p p , 즉

• \epsilon n ϵ n 노드는 모두 허용하고
• 데이터를 완전히 사용할 수 없습니다. 즉, 질의를 통해 데이터를 재구성할 수 없습니다.

우리의 목적을 위해, p p 는 (어떤 적대자에 대해서든) 최대 2^{-30} 2 − 30 이 되기를 원합니다. 아래에서, n n , \epsilon ϵ , 그리고 인코딩 방식에 따라 노드당 쿼리 수 k k 를 설정하여 p \leq 2^{-30} p ≤ 2 − 30 이 보장되도록 하겠습니다.

\epsilon ϵ 의 영향 및 선택 :
위에서 설명한 보안 개념은 \epsilon \in (0, 1] ϵ ∈ ( 0 , 1 ] 로 매개변수화되며, 이는 적대자가 속이려 는 노드의 비율을 모델링합니다. 형식적 정의 와 간단한 암호화 축소를 통해 주어진 \epsilon ϵ (고정된 n n )에 대한 부분 집합 건전성은 더 큰 \epsilon' \geq \epsilon ϵ ′ ≥ ϵ 에 대한 부분 집합 건전성을 의미합니다 . 다시 말해, 적대자가 \epsilon ϵ - 분수의 노드를 속일 수 없다면 더 큰 분수의 \epsilon' ϵ ′ 를 속일 수 없다는 것은 확실합니다.

하지만 이것이 전체 합의 프로토콜과 어떤 관련이 있을까요? 공격자가 노드의 \epsilon ϵ 분율보다 많은 노드를 속일 수 없다고 가정해 보겠습니다. 속은 각 노드는 합의 과정에서 사실상 추가적인 악성 노드 로 동작합니다. 따라서 데이터 가용성 샘플링을 사용하면 공격자는 최대 \epsilon ϵ 분율의 추가적인 악성 노드를 확보하게 됩니다.

예를 들어, DAS가 없는 합의가 최대 <{1}/{3} < 1 / 3개의 악성 노드를 허용하는 경우 DAS가 있는 경우 시스템은 이제 최대 <{1}/{3} - \epsilon < 1 / 3 − ϵ 개의 악성 노드만 허용할 수 있습니다.

따라서 실제로는 적대자의 영향력이 무시할 수 있을 정도로 작게 하려면 \epsilon ϵ을 작게 선택해야 합니다. 예를 들어 \epsilon = 1\% ϵ = 1 % .

II. PeerDAS - 1D 구성

이 섹션에서는 Fusaka 업그레이드에 포함될 PeerDAS의 작동 방식을 설명합니다. 또한, 셀 수준 메시징을 통해 부분 재구성을 어떻게 지원하는지 설명합니다.

작동 원리

우리는 "암호화 계층"과 관련된 모든 것(예: 약속 및 개방)을 무시하고 데이터를 인코딩하는 방법과 클라이언트가 쿼리를 만드는 방법을 설명합니다.

블롭은 m m 개의 셀로 구성된 집합으로, 각 셀은 f f 개의 필드 요소를 가집니다. PeerDAS의 현재 매개변수 설정에서는 셀당 f = 64 , f = 64 개의 필드 요소와 블롭당 m = 64 개의 셀 이 있습니다. 다양한 셀 크기를 고려하기 위해 fm = 4096 , f m = 4096을 상수로 두고(즉, 데이터 크기를 고정), f \in \{64,32,16,8\} f ∈ { 64 , 32 , 16 , 8 }을 변경하여 m = 4096 / f m = 4096 / f 로 설정합니다.

단일 블롭을 인코딩하려면 1/2 1/2 비율 의 리드-솔로몬 코드를 사용하여 블롭을 확장합니다 . 그 결과 2m x 2m 개의 셀, 즉 2fm = 8192 x 2fm = 8192 개의 필드 요소가 생성됩니다. PeerDAS에서는 이 인코딩 과정을 b b 개의 블롭에 독립적으로 적용하고, 확장된 블롭을 b \times 2m b × 2m 셀 행렬의 행으로 간주합니다.

이제 클라이언트는 이 행렬의 전체 열을 쿼리합니다 . 즉, b 개의 셀을 한 번에 다운로드하려고 시도합니다. 이는 "심볼" 또는 삭제 코드가 확장된 블롭 행렬의 열임을 의미합니다. 이러한 열 중 m 개 에서 전체 행렬과 데이터를 재구성할 수 있습니다.

샘플링 기능을 지원하는 구체적인 네트워킹 인프라는 열에 대한 GossipSub 주제 입니다. 즉, 특정 샘플(= 열)에 관심이 있는 노드만 참여하는 하위 네트워크입니다.

부분 재건

예상대로 현재 PeerDAS 설계는 부분 재구성을 지원하지 않습니다 . 그러나 PeerDAS처럼 여러 블롭에 독립적으로 적용할 경우 , 이러한 1차원 인코딩조차도 원칙적으로 이 기능을 지원할 수 있습니다. 실제로 셀과 같이 열보다 작은 수직 단위를 사용하면 전체 행렬의 일부(예: 개별 행 또는 행 그룹)만 재구성하는 것이 가능합니다. 이는 두 가지 과제를 야기합니다.

1. 부분적 재시드 : 노드가 단일 행을 재구성할 때 전체 샘플(열)을 재구성하지는 않지만 여전히 재구성된 데이터를 네트워크에 다시 제공할 수 있어야 합니다.
2. 재구성에 필요한 충분한 셀 확보 : 열만 샘플링하는 경우, 재구성 능력은 전부 아니면 전무입니다. 즉, 노드가 전체 행렬을 재구성할 만큼 충분한 열을 확보하거나, 아니면 그 일부를 재구성할 수 없습니다. 다시 말해, 슈퍼노드만 재구성에 참여할 수 있습니다. 노드가 전체 데이터의 일부만 다운로드하면서도 재구성에 참여할 수 있도록 하고 싶습니다.

이러한 접근 방법에는 잘 알려진 방법이 있으며, 이를 통해 부분적인 재구성을 얻을 수 있습니다.

1. 셀 수준 메시징 : 노드가 전체 열이 아닌 셀을 교환할 수 있도록 하여 행을 재구성하는 노드가 최소한 참여하는 열 토픽에서 셀 단위로 다시 시드할 수 있습니다.
2. 행 토픽 : 노드가 셀 수준 메시징 기능을 갖춘 행 토픽에 참여하여 일부 행을 다운로드하려고 시도합니다. 중요한 것은 이것이 샘플링이 아니며, 획득하는 행 수에 대한 보안 문제가 없으므로 단일 행 토픽에 참여하더라도 충분합니다. 실제로 1차원 구조에서는 수직 중복성이 없으므로 행 샘플링은 무의미합니다. 행 토픽의 목적은 열 토픽의 셀이 슈퍼노드 없이도 행 토픽으로 유입되어 행 단위 재구성을 가능하게 하는 것입니다. 재구성된 셀은 행 토픽에서 모든 열 토픽으로 유입될 수 있으며, 이 경우에도 단일 노드가 모든 셀에 참여할 필요는 없습니다.

참고: 수직 중복성이 부족하므로 모든 행 토픽이 재구성 작업을 성공적으로 수행해야 합니다. 단 하나의 행 토픽이라도 재구성 작업에 실패하면(예: 해당 토픽에 국한된 네트워크 수준의 공격으로 인해) 전체 재구성이 완료될 수 없습니다.

샘플 수

이제 PeerDAS의 클라이언트당 샘플 수 k k 를 결정해 보겠습니다. 위에서 논의한 바와 같이, 공격자가 부분집합 건전성을 위반할 확률 p p 가 최대 2^{-30} 2 − 30 이 되도록 k k 를 선택하고자 합니다.

PeerDAS의 보안은 여기 와 여기에서 광범위하게 분석되었습니다. 후자의 연구는 여기 의 보안 프레임워크를 기반으로 하며, 보조정리 1과 보조정리 3을 결합하여 부분집합 건전성에 대한 구체적인 경계를 도출할 수 있습니다. 궁극적으로 이 모든 과정을 통해 부분집합 건전성에 대한 동일한 경계를 도출할 수 있습니다. 즉, 다음과 같습니다 .

p \leq \binom{n}{n\epsilon}\cdot \binom{2m}{m-1} \cdot (\frac{m-1}{2m})^{kn\epsilon} \leq \binom{n}{n\epsilon}\cdot \binom{2m}{m-1} \cdot 2^{-kn\epsilon}. p ≤ ( n n ϵ ) ⋅ ( 2 m m − 1 ) ⋅ ( m − 1 2 m ) k n ϵ ≤ ( n n ϵ ) ⋅ ( 2 m m − 1 ) ⋅ 2 − k n ϵ .

직관적으로, 첫 번째 이항식은 적대자가 속일 n\epsilon n ϵ 노드를 자유롭고 적응적으로 선택할 수 있는 능력을 설명하고, 두 번째 이항식은 적대자가 이러한 노드에서 사용할 수 있도록 m-1 m − 1개의 심볼을 선택하는 것을 설명하며, 마지막 항은 모든 샘플이 인코딩의 이 사용 가능한 부분에 포함될 확률입니다.

p \leq 2^{-30} p ≤ 2 − 30 이고 n,m,\epsilon n , m , ϵ가 주어지기를 원한다면 다음을 설정해야 합니다.

k \geq \frac{1}{n\epsilon} \left( \log_2 \binom{n}{n\epsilon} + \log_2 \binom{2m}{m-1} + 30 \right) k ≥ 1 n ϵ ( 로그 2 ( n n ϵ ) + 로그 2 ( 2 m m − 1 ) + 30 ) .

k k를 계산하는 코드는 다음과 같습니다.

 from math import comb, log2, ceil # used later from tabulate import tabulate # used later import numpy as np # used later import matplotlib.pyplot as plt # used later def min_samples_per_node ( n: int , m: int , r: int = 2 , eps: float = 0.01 ): """Finds the smallest integer k such that k samples per nodeachieve security of 30 bits for the 1D construction.Inputs:n: total number of nodesm: number of symbols in original datar: inverse coding rate (total symbols = r*m), default=2eps: fraction of nodes to be fooled (0 < eps <= 1), default=0.01Returns:Smallest integer k satisfying the bound""" neps = int (n * eps)binom_n = comb(n, neps)binom_m = comb(m*r, m- 1 )log2_binom = log2(binom_n) + log2(binom_m)k = -(log2_binom + 30 )/(n*eps*log2( 1 /r)) return ceil(k)

III. 2D 구조

PeerDAS의 대안은 2차원 구조로, 이미 논의된 바 있습니다( 여기 , 여기 , 여기 ). 이 구조는 리드-솔로몬 코드의 텐서 코드를 기반으로 하며, 8절에서 분석되었습니다. 이 구조는 자연스러운 형태의 부분 재구성을 지원합니다.

작동 원리

PeerDAS는 b \times m b × m 행렬(블롭당 m m개의 셀이 있는 b b 개의 블롭)을 수평으로 확장하여 b \times 2m b × 2 m 크기 의 셀 행렬로 표현할 수 있습니다. 즉, 이는 각 셀이 f f 개의 필드 요소를 포함하는 b \times 2mf b × 2 m f 크기의 필드 요소 행렬입니다. 확장은 수평축을 따라서만 이루어지므로 PeerDAS는 1차원 구조라고 합니다.

2차원 구성에서는 다음과 같이 진행합니다. PeerDAS에서처럼 유도된 b \times 2mf