제가 꽤 오랫동안 작업해 온 게 있어요. 완벽하진 않지만, 최대한 개인 정보를 보호하는 멀티시그 방식이에요. 여러분의 의견을 듣고 싶어요!

제가 쓴 다른 관련 연구 논문도 꼭 확인해 보세요: 기밀로 포장된 이더리움 과 ZEX: 기밀 피어투피어 DEX .

또한, 훌륭한이더리움 개인정보 보호 로드맵 도 살펴보세요.

추상적인

본 논문은 집단 의사 결정의 프라이버시와 기밀성을 보호하기 위해 영지식(ZK) EVM 기반 다중 서명 지갑을 구현하는 실용적인 접근법을 제안합니다. 이 접근법은 세 가지 핵심 기능을 결합합니다. 익명성을 위한 머클 트리 멤버십 증명, 편향 없는 의사 결정을 통해 참여자 투표 기밀성을 보장하는 통합 ECC ElGamal 암호화, 그리고 중앙 집중형 신뢰 개체의 키 추론 및 제거 시 상호 작용이 없는 분산 키 생성(DKG)을 구현합니다.

제안된 솔루션은 Solidity 스마트 계약과 ZK 회로로 구성됩니다. 전자는 계정 팩토리 역할을 하며, 사용자가 멀티시그를 생성하고 공동 제안을 실행하기 위해 상호작용하는 실제 계정 역할을 합니다. 후자는 사용자가 멀티시그 세트에 속하는지 확인하고 제안 실행 여부에 대한 결정을 중간 결과 공개 없이 검증합니다.

제안된 접근 방식의 단점은 결과를 계산하기 위해 모든 다중 서명 참여자가 제안에 투표해야 한다는 것입니다.

1. 서론

퍼블릭 블록체인의 투명성은 향상된 추적성, 실행 검증 가능성, 그리고 누구나 이용할 수 있는 데이터의 개방성 등 다양한 이점을 제공합니다. 그러나 다자간 의사 결정, 특히 안전하고 공정한 멀티시그 지갑의 핵심 요소인 개인정보 보호 및 투표 편향 방지 측면에서 고유한 과제를 안고 있습니다.

목표는 회원에 대한 어떤 정보도 공개하지 않고 멀티시그 투표자에게 투표용지가 비밀로 유지되고, 조기 참여자의 투표 방식에 따라 선택이 영향을 받지 않는다는 확신을 제공하는 간단하고 허가가 필요 없는 멀티시그를 만드는 것입니다.

다중 서명을 통해 사용자는 회원 목록에 포함되거나 제외될 수 있으며, "서명 임계값"을 설정하고, 공동으로 승인된 거래를 실행할 수 있으며, 개인정보 보호는 (거의) 전혀 침해되지 않습니다. 또한, 회원 목록에 있는 모든 사용자가 투표를 완료할 때까지 사용자는 개별 투표 내용이나 결과를 알지 못한 채 제안에 찬성 또는 반대 투표를 할 수 있습니다.

물론, 가장 중요한 제한 사항은 마지막 투표 참여자가 투표를 하고 공개하기 전에 진행 중인 제안의 방향을 해독하고 볼 수 있다는 것입니다.

2. 사양

2.1. 애플리케이션 흐름

기술적인 심층 분석을 진행하기 전에 전반적인 그림을 살펴보고 기본적인 애플리케이션 흐름을 이해하는 것이 중요합니다. 다중 서명 지갑 생성, 제안서 생성, 그리고 제안서 투표를 통한 일반 다중 서명 거래 실행 흐름이 제공됩니다.

2.1.1. 멀티시그 생성

이 애플리케이션의 핵심은 멀티시그 지갑입니다. 사용자는 애플리케이션과 상호 작용하면서 비즈니스 로직에 따라 허용된 투표자 목록을 사용하여 멀티시그를 생성합니다.

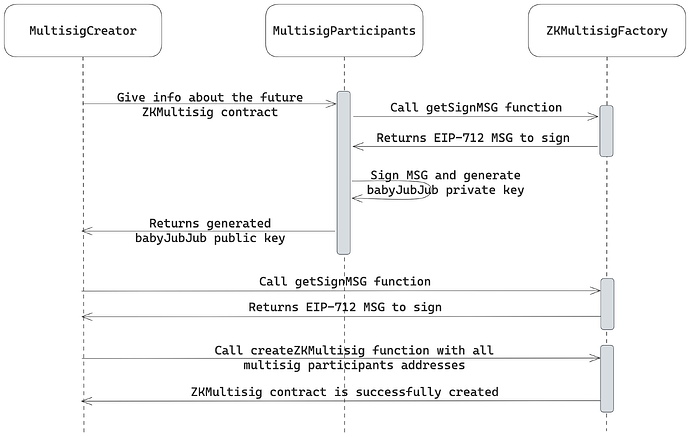
다중서명 생성 흐름은 다음 다이어그램에 나와 있습니다.

그림 1: ZKMultisig 계약 생성 흐름 3159×2003 245KB

1. 생성 과정은 사용자(지갑 생성자)가 허용 목록에 추가할 투표자들의 공개 키를 수집하는 것으로 시작됩니다. 다중 서명은 개인정보 보호를 위해 ZK(영문 키 인증)를 활용하므로, 모든 사용자는 애플리케이션을 사용하기 전에 고유 식별자로 사용될 babyJubJub 키 쌍을 생성해야 합니다.

   이러한 키를 생성하려면 사용자는 EIP-712 구조화된 메시지에 이더리움(ECDSA) 개인 키로 서명하고, 생성된 서명을 해싱합니다. 해싱 결과인 babyJubJub 개인 키는 다음과 같습니다.

   사용자는 참여하려는 모든 멀티시그에 대해 고유한 공개 키를 얻기 위해 고유한 메시지에 서명하는 것(개인정보 보호 강화)이나 플랫폼 전반에서 사용할 단일 공개 키를 고수하는 "기본" 메시지를 사용하는 것(UX가 더 좋아질 수 있음) 중에서 선택할 수 있습니다.

2. 필요한 모든 babyJubJub 공개 키를 획득한 지갑 생성자는 ZKMultisigFactory 스마트 계약에서 지갑 생성 함수를 호출하여 허용 목록에 추가할 모든 공개 키를 제공합니다. 내부적으로, 멀티시그는 참여자를 희소 머클 트리(SMT) 데이터 구조에 저장하여 ZK 증명 가능한 멤버십 증명과 저렴한 목록 유지 관리를 가능하게 합니다.

3. 멀티시그 지갑이 배포되면 회원은 제안을 만들고 회원 자격에 대한 ZK 증명을 생성하고 EdDSA 블라인더를 적용하여 재사용 불가능한 결정을 내려 투표할 수 있습니다.

설명된 접근 방식을 사용하면 결정적 키 유도 함수(KDF)를 통해 사용자의 실제 "지갑 주소"를 babyJubJub 주소로 추상화하여 사용자의 완전한 개인 정보 보호를 달성하고 의사 결정 주소를 결정할 확률을 1에서 1/N 1 / N 으로 줄일 수 있습니다. 여기서 N N 은 멀티시그 구성원의 수입니다.

2.1.2 제안서 생성

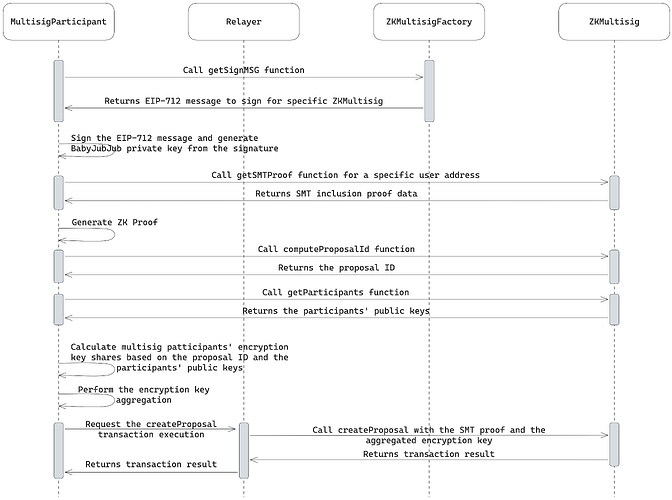
제안서 작성 흐름은 아래 다이어그램에 나와 있습니다.

그림 2: 멀티시그 제안 생성 흐름 4360×3240 434KB

1. 제안 생성자(멀티시그 허용 목록에 있는 사용자)는 "멀티시그 지갑 생성" 단계에서 babyJubJub 키 쌍을 확실하게 복구하여 애플리케이션에 로그인합니다.

   KDF 알고리즘은 동일하게 유지됩니다. EIP-712 구조화된 메시지는 ZKMultisigFactory 에서 가져온 후 서명되고, 서명은 해싱되어 babyJubJub 개인 키를 계산합니다.

2. 사용자는 SMT 포함 증명을 통해 멀티시그에 대한 멤버십을 허가 없이 검증하는 ZK 증명을 생성합니다.

3. 제안 생성자는 일회성 집계 암호화 키 생성에 사용될 제안의 ID를 계산합니다.

4. 생성자는 제안 ID와 참여자의 babyJubJub 공개 키를 기반으로 KDF를 사용하여 모든 멀티시그 참여자의 암호화 키 공유량을 비대화적으로 계산합니다.

5. 생성자는 모든 암호화 키 공유를 계산한 후 이를 최종 암호화 키로 집계합니다.

6. 제안 생성자는 릴레이어를 통해 createProposal 함수를 호출하여 SMT 포함 증명과 투표 암호화에 사용될 집계 키를 제공합니다.

제안이 생성된 후, 다중서명 참여자는 투표를 시작할 수 있습니다.

2.1.3. 제안에 대한 투표

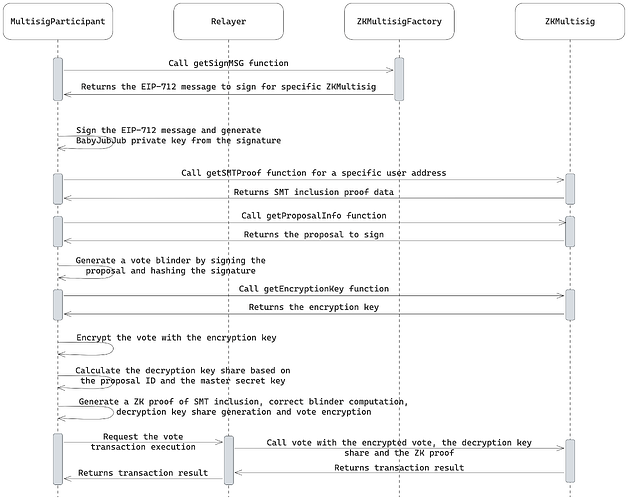
제안 흐름에 대한 투표는 다음 다이어그램에 표시되어 있습니다.

그림 3: 다중 서명 제안 투표 흐름 4120×3280 468KB

1. SMT 포함(Merkle) 증명은 사용자가 멀티시그의 회원임을 나타내기 위해 계약에서 가져옵니다.

2. 사용자는 투표할 제안서에 (babyJubJub 개인 키로) 서명하여 획득한 EdDSA 서명을 해싱하여 블라인더를 생성합니다. 이는 사용자가 이전에 동일한 제안서에 투표한 적이 없음을 확인하는 데 사용됩니다.

3. 사용자는 제안서의 암호화 키를 가져옵니다.

4. 수신된 임시 암호화 키는 투표를 암호화하는 데 사용됩니다.

5. 제안 ID를 기반으로 사용자는 babyJubJub 개인 키와 KDF를 사용하여 복호화 키 공유를 계산합니다.

6. 필요한 모든 데이터를 계산한 후, 멀티시그 참여자는 릴레이어를 통해 vote 기능을 호출하여 암호화된 투표, 복호화 키 공유, ZK 증명을 제공합니다.

7. 스마트 계약은 제공된 복호화 키 공유를 집계 가능한 최종 복호화 키에 추가하고 투표가 성공적으로 실시된 것으로 설정합니다.

2.1.4 투표 공개 및 제안 실행

마지막 참여자가 투표를 완료해야만 복호화 키가 완성되어 투표 결과를 공개하는 데 사용할 수 있습니다. 이는 reveal 함수를 호출하여 수행됩니다. 이 함수는 집계된 투표를 복호화하고 투표 결과에 따라 제안 상태를 변경합니다. "찬성" 투표 수가 "서명 임계값"을 초과하면 제안은 "승인"으로 설정되어 실행될 수 있고, 그렇지 않으면 "거부"됩니다.

아래 다이어그램은 투표 공개 프로세스를 보여주며, 복호화와 실행 논리를 단일 함수 revealAndExecute 로 캡슐화합니다.

그림 4: 다중 서명 제안 투표 공개 흐름 2390×1540 169KB

2.2. 암호화 수학

이 섹션에서는 프로토콜에서 사용되는 투표 암호화 논리의 수학적 기초를 제공합니다.

2.2.1. 타원 곡선 산술 연산

이 문서의 맥락에서 특정 연산은 타원 곡선에서 수행되며 기존 산술과 구별되는 특정 수학 연산을 포함합니다.

• 점 추가 P + Q P + Q 는 타원 곡선 위의 점인 경우 정의된 군 연산 논리에 따라 수행됩니다.
• 스칼라 곱셈 k \times P k × P 는 k k 가 스칼라이고 P P 가 타원 곡선 위의 점일 때 점 P P 를 자기 자신에 k k 번 더하는 것을 의미합니다.
• 점 뺄셈 P - Q P − Q , 여기서 P P 와 Q Q 는 타원 곡선 위의 점이며 P + (-Q) P + ( − Q ) 와 동일합니다. 여기서 -Q − Q 는 점 Q Q 의 역입니다.

2.2.2. 암호화 키용 KDF

이 프로토콜은 결정론적 KDF로 스텔스 키 스키마 CoM17[1]을 사용합니다. 이러한 스키마를 사용하면 마스터 키에서 각 제안에 대한 투표를 암호화하고 복호화하기 위한 고유 키 공유를 생성할 수 있습니다.

마스터 키 쌍은 다음을 만족해야 합니다.

pk = sk \times G, p k = s k × G ,

여기서 pk p k — 마스터 공개 키,
sk s k — 마스터 시크릿 키,
G G — 타원 곡선의 기준점.

지갑 생성 과정에서 생성된 babyJubJub 키 쌍은 ElGamal 암호화 및 복호화 키의 마스터 키 쌍으로 사용됩니다. 키 도출 절차는 아래와 같습니다.

먼저, 챌린지는 제안 ID를 기반으로 계산됩니다. 다중 서명은 ZKP 재전송 및 프런트러닝 공격을 방지하기 위해 제안의 증분 열거를 의도적으로 생략합니다. 이는 제안 생성자에게 생성 중인 제안의 챌린지에 서명하도록 요청함으로써 가능합니다. 제안 ID와 챌린지는 다음과 같이 결정론적으로 계산됩니다.

 proposalId = keccak256(abi.encode(target, value, data, salt));challenge = poseidon(uint248(keccak256(abi.encode(chainid, zkMultisigAddress, proposalId))));

r r 이 도전과 같고 R R 이 도전 지점이라고 하자.

R = r \times G R = r × G

암호화 키 공유는 다음과 같이 도출됩니다.

P_i = 포세이돈 ( r × pk_i ) × G + pk_i P i = 포세이돈 ( r × pk_i ) × G + pk_i

이에 따라 복호화 키 공유는 다음과 같이 도출됩니다.

x_i = (포세이돈 ( sk_i × R ) + sk_i ) \ mod n x i = ( 포세이돈 ( sk_i × R ) + sk_i ) 모드 N

여기서 n n 은 타원 곡선의 순서입니다.

키 유도 방식의 일관성은 다음을 통해 증명할 수 있습니다.

P_i = x_i \times G = (포세이돈(sk_i \ times R ) + sk_i ) \ times G = P i = x i × G = ( 포세이돈 ( sk_i × R ) + sk_i ) × G =
= 포세이돈(sk_i \cdot r \times G) \times G + sk_i \ times G = 포세이돈 ( r \ times pk_i ) \ times G + pk_i = 포즈 아이 돈 ( sk i ⋅ r × G ) × G + sk i × G = 포즈 아이 돈 ( r × pki ) × G + pki

2.2.3. ECC ElGamal 암호화 체계

이 프로토콜은 ElGamal 암호화 방식[2]의 타원 곡선 암호화(ECC) 수정을 활용하여 다중 서명 투표를 암호화하고 이후에는 암호 해독합니다.

집계된 암호화 키 P P는 모든 암호화 키 공유를 합산하여 계산된 타원 곡선의 점입니다.

P = \sum_{i=1}^N P_i, P = ∑ N i = 1 P i ,

여기서 N N — 다중 서명 참여자 수,
P_i P i — 암호화 키 공유(타원 곡선 점).

참가자의 투표는 타원 곡선 상의 점 M M 에 매핑됩니다. 생성점 G G 는 "찬성" 투표로, 무한대점은 "반대" 투표로 사용됩니다. 0<k<n 0 < k < n 을 만족하는 난수 k k 가 선택됩니다. 이후, 암호문 ( C_1 C 1 , C_2 C 2 )은 다음과 같이 계산됩니다.

C_1 = k × G C 1 = k × G
C_2 = M + k × P C 2 = M + k × P

투표를 해독하려면 먼저 집계된 해독 키 공유를 계산합니다.

x = \sum_{i=1}^N x_i \mod n, x = ∑ N i = 1 x i 모드 N ,

여기서 n n — 타원 곡선의 순서,
x_i x i — 복호화 키 공유(스칼라).

그런 다음 계산된 집계된 복호화 키 x x를 사용하여 메시지 지점 M M 을 복구합니다.

M = C_2 - x \times C_1 M = C 2 − x × C 1

ECC ElGamal 체계 내 키 집계의 일관성은 다음과 같이 증명할 수 있습니다.

P = \sum_{i=1}^N P_i = \sum_{i=1}^N x_i \times G P = ∑ N i = 1 P i = ∑ N i = 1 x i × G

D = x \times C_1 = \sum_{i=1}^N x_i \times C_1 = \sum_{i=1}^N x_i \cdot k \times G = k \times (\sum_{i=1}^N x_i \times G) = k \times P D = x × C 1 = ∑ N i = 1 x i × C 1 = ∑ N i = 1 x i ⋅ k × G = k × ( ∑ N i = 1 x i × G ) = k × P

M = C_2 - D = M + k × P - k × P M = C 2 − D = M + k × P − k × P

2.2.4. 투표의 동형 집계

점 G G 와 무한대를 투표로 사용하면 각 투표 동안 암호화된 투표를 합산하여 누적 투표 결과를 준동형으로 형성할 수 있습니다.

SC_1 = \sum_{i=1}^N C_{1_i} S C 1 = ∑ N i = 1 C 1 i
SC_2 = \sum_{i=1}^N C_{2_i} S C 2 = ∑ N i = 1 C 2 i

합계를 복호화하여 집계된 결과 T T를 얻습니다.

T = \sum_{i=1}^N M_i = SC_2 - x \times SC_1 T = ∑ N i = 1 M i = S C 2 − x × S C 1

복호화된 총 T T 는 v \times G v × G 와 같습니다. 여기서 v v 는 제안에 "찬성" 투표한 총 유권자 수입니다.

투표 결과를 공개하기 위해 멀티시그 참여자는 가능한 스칼라 값 v_i v i 를 오프체인으로 반복해야 합니다. 여기서 0 \leq v_i \leq N 0 ≤ v i ≤ N 이며 다음 방정식을 만족하는 값을 찾습니다.

v_i \times G = T v i × G = T

그런 다음 이 값을 스마트 계약에 제출하면 위의 방정식이 확인됩니다.

• v < signaturesQuorum v < signaturesQuorum 이면 제안 에 " 찬성 " 투표 한 참여자 가 충분 하지 않아 제안 의 상태가 "거부됨"으로 설정됩니다.
• v \geq signaturesQuorum v ≥ sign a t u r e s Quorum 이면 충분한 수 의 참여자 가 제안 에 "찬성" 투표했으며 해당 제안의 상태는 "수락됨"으로 설정됩니다.

2.2.5. 체인상 암호화 키 계산

제안이 생성되면 개별 공개 키와 챌린지에서 집계된 암호화 키가 올바르게 계산되었는지 확인하는 것이 필수적입니다.

이 값은 공개적으로 계산 가능하므로 스마트 계약에서 참여자의 마스터 공개 키를 반복하여 암호화 지분을 도출하여 평가할 수 있습니다. 그러나 이 방법은 최적이 아니며, 모든 참여자의 마스터 공개 키의 합을 나타내는 누적 공개 키를 도입하여 개선할 수 있습니다. 이 키는 스마트 계약에 저장되며 멤버십 목록이 업데이트될 때마다 업데이트되어야 합니다.

각 참가자의 암호화 키 공유를 개별적으로 계산하는 대신:

P_i = 포세이돈 ( r × pk_i ) × G + pk_i P i = 포세이돈 ( r × pk_i ) × G + pk_i

해시 부분만 계산하고 이를 이전 해시의 합계에 더하면 루프 내부의 작업 수가 줄어듭니다.

sumHash = sumHash + poseidon ( r \ times pk_i ) sumHash = sumHash + poseidon ( r × pki )​​​​​​​​​​​

그러면 집계된 암호화 키는 다음과 같이 계산될 수 있습니다.

aggKey = sumHash \ times G + cumulativePk agg Key = sumHash × G + cumulativePk​​​​​​​​​​​​​​

2.3. 기능

이 섹션에서는 스마트 계약 및 회로에 대한 기술적 설명을 제공합니다. 또한, 실행 가능한 프로토타입을 구현하기 위해 구성 요소가 지원해야 하는 필수 기능을 간략하게 설명합니다.

2.3.1. ZK멀티시그팩토리

애플리케이션에는 ZKMultisigFactory 와 ZKMultisig 두 가지 계약이 있습니다. 이 팩토리는 멀티시그 지갑을 생성하고 키 도출 절차에 필요한 EIP-712 메시지를 생성하는 데 사용됩니다. ZKMultisig 지갑 자체의 구현입니다.

ZKMultisigFactory 인터페이스는 다음과 같이 정의됩니다.

 interface IZKMultisigFactory {event ZKMultisigCreated(address indexed zkMultisigAddress,uint256[2][] initialParticipants,uint256 initialQuorumPercentage);function createZKMultisig(uint256[2][] calldata participants,uint256 quorumPercentage,uint256 salt) external returns (address);function computeZKMultisigAddress(address deployer,uint256 salt) external view returns (address);function getKDFMSGToSign(address zkMultisigAddress) external viewreturns (bytes32);function getDefaultKDFMSGToSign() external view returns (bytes32);function isZKMultisig(address multisigAddress) external view returns(bool);}

ZKMultisigFactory 지갑을 직접 배포하지 않고 ERC-1967 프록시를 배포합니다. 또한, create2 방식을 사용하여 지갑 주소에 대한 결정성을 확보하고 KDF 메시지를 사전에 생성합니다.

create2의 salt는 다음과 같이 정의됩니다.

 realSalt = keccak256(abi.encode(msg.sender, salt));

사용자는 어떤 KDF 메시지에 서명할지 결정할 수 있습니다.

• 지갑당 고유한 메시지(개인정보 보호 가정 증가)
• 기본 설정(UX가 더 좋을 수 있음).

반환된 메시지의 구조는 섹션 2.3.6에서 확인할 수 있습니다.

2.3.2 ZK멀티시그

ZKMultisig 는 멀티시그 기능을 구현하는 컨트랙트입니다. 구현에는 멀티시그 참여자 관리, 쿼럼 설정, 제안 생성, 투표 및 실행이 포함됩니다. ZKMultisig 인터페이스는 다음과 같이 정의됩니다.

 import "@solarity/solidity-lib/libs/data-structures/SparseMerkleTree.sol";interface IZKMultisig {enum ProposalStatus {NONE,VOTING,ACCEPTED,REJECTED,EXPIRED,EXECUTED}struct ZKParams {uint256[2] a;uint256[2][2] b;uint256[2] c;uint256[] inputs;}struct ProposalContent {address target;uint256 value;bytes data;}struct ProposalInfoView {ProposalContent content;ProposalStatus status;uint256 proposalEndTime;uint256 votesCount;uint256 requiredQuorum;}event ProposalCreated(uint256 indexed proposalId, ProposalContent content);event ProposalVoted(uint256 indexed proposalId, uint256 voterBlinder);event ProposalExecuted(uint256 indexed proposalId);function addParticipants(uint256[2][] calldata participantsToAdd) external;function removeParticipants(uint256[2][] calldata participantsToRemove) external;function updateQuorumPercentage(uint256 newQuorumPercentage) external;function create(ProposalContent calldata content,uint256 duration,uint256 salt,ZKParams calldata proofData) external returns (uint256);function vote(uint256 proposalId,bytes calldata encryptedVote,uint256 decryptionKeyShare,ZKParams calldata proofData) external;function reveal(uint256 proposalId, uint256 approvalVoteCount) external;function execute(uint256 proposalId) external;function revealAndExecute(uint256 proposalId,uint256 approvalVoteCount) external;function getPerticipantsSMTRoot() external view returns (bytes32);function getParticipantsSMTProof(bytes32 publicKeyHash)external view returns (SparseMerkleTree.Proof memory);function getParticipantsCount() external view returns (uint256);function getParticipants() external view returns (uint256[2][] memory);function getProposalsCount() external view returns (uint256);function getProposalsIds(uint256 offset, uint256 limit)external view returns (uint256[] memory);function getQuorumPercentage() external view returns (uint256);function getEncryptionKey(uint256 proposalId) external viewreturns (uint256[2] memory);function getProposalInfo(uint256 proposalId) external viewreturns (ProposalInfoView memory);function getProposalStatus(uint256 proposalId) external viewreturns (ProposalStatus);function getProposalChallenge(uint256 proposalId)external view returns (uint256);function computeProposalId(ProposalContent calldata content,uint256 salt) external view returns (uint256);function isBlinderVoted(uint256 proposalId,uint256 blinderToCheck) external view returns (bool);}

주어진 제안에 대해 createProposal 함수 내에서 ElGamal 암호화 키 집계를 검증하는 것이 중요합니다. 스마트 계약은 활성 멤버의 마스터 공개 키를 반복하여 암호화 키 공유를 도출하고, 이를 다시 암호화 키로 집계해야 합니다(2.2.5절 참조).

2.3.3 제안 생성 회로

본 논문의 모든 매개변수는 증명 가능하고 영지식 회로와 호환되도록 설계되었습니다. 제안 생성 증명을 위한 회로 신호 목록은 다음과 같습니다.

공공 신호:

• SMT 루트(입력)
• 제안 ID(입력).

개인 신호:

• 마스터 비밀 키;
• 마스터 공개 키 [선택 사항]
• SMT 포함 증명.

이러한 신호를 활용하려면 회로에 다음과 같은 제약 조건이 있어야 합니다.

• 제공된 마스터 비밀 키는 실제로 제공된 마스터 공개 키의 비밀 키입니다.
• 마스터 공개 키는 SMT 루트에 고정되어 SMT에 속합니다.

2.3.4. 제안 투표 회로

제안 투표 증명을 위한 회로 신호 목록은 다음과 같습니다.

공공 신호:

• 사용자 블라인더(출력);
• 복호화 키 공유(출력)
• 암호화 지점 C_1 C 1 (출력);
• 암호화 지점 C_2 C 2 (출력);
• 집계된 암호화 키(입력)
• 제안에 대한 이의 제기(입력);
• SMT 루트(입력).

개인 신호:

• 마스터 비밀 키;
• 마스터 공개 키 [선택 사항]
• EdDSA 챌린지의 마스터 서명;
• 실제 투표: G G 지점 또는 무한대 ;
• 무작위 암호화 값 k k ;
• SMT 포함 증명.

이러한 신호를 활용하려면 회로에 다음과 같은 제약 조건이 있어야 합니다.

• 제공된 마스터 비밀 키는 실제로 제공된 마스터 공개 키의 비밀 키입니다.
• 마스터 공개 키는 SMT 루트에 고정되어 SMT에 속합니다.
• EdDSA 챌린지의 마스터 서명은 마스터 공개 키와 대조하여 검증됩니다.
• 서명의 포세이돈 해시는 사용자 블라인더와 같습니다.
• 마스터 비밀 키와 제안 챌린지가 주어지면 복호화 키 공유가 올바르게 계산됩니다(섹션 2.2.2 참조).
• 제공된 투표는 G G 또는 inf i n f 와 같습니다.
• 집계된 암호화 키, 난수 암호화 값 k k 및 투표가 주어지면 암호화가 올바르게 수행되었습니다(섹션 2.2.3 참조).

2.3.5. KDF

키 유도 함수(KDF)는 특정 입력으로부터 babyJubJub 개인 키를 결정론적으로 생성하는 함수입니다. 이 경우, 입력은 EIP-712 형식 메시지의 이더리움 ECDSA 서명입니다.

KDF는 다음과 같이 정의됩니다.

 message = getKDFMSGToSign() or getDefaultKDFMSGToSign();signature = eth_signTypedData_v4(message);privateKey = keccak256(keccak256(signature));

개인 키는 서명에서 직접 파생되므로 서명을 공개하지 않는 것이 중요합니다.

2.3.6. KD EIP-712 메시지

키 파생 EIP-712 메시지를 생성하기 위해 계약의 ZKMultisig 주소를 포함하는 KDF 메시지 유형 해시가 사용됩니다. 네트워크와 계약 정보가 표준 EIP-712 도메인 구조에 포함되어 있으므로 이것으로 충분합니다.

 bytes32 KDF_MSG_TYPEHASH = keccak256("KDF(address zkMultisigAddr)");bytes32 kdfStructHash = keccak256(abi.encode(KDF_MSG_TYPEHASH, zkMultisigAddress));

getKDFMSGToSign() 및 getDefaultKDFMSGToSign() 함수는 위에서 설명한 대로 EIP-712 메시지를 생성합니다. getDefaultKDFMSGToSign() 함수는 기본 메시지 생성에 0 주소를 사용합니다.

2.3.7. 릴레이어

위의 접근 방식은 거래가 전송되는 EVM 주소와 완전히 독립적이므로, 사용자는 익명성을 유지하기 위해 다양한 릴레이어를 활용할 수 있습니다. GSN과 같은 프로토콜 친화적인 릴레이어를 사용할 수도 있지만, 프런트엔드에 추가적인 통합 로직이 필요합니다.

3. 근거

ElGamal 암호화 체계[2]의 ECC 수정은 키 유도 함수(KDF) 및 키 집계와의 호환성을 위해 선택되었습니다. ElGamal의 비결정적 특성은 난수 값 k k 에 의해 도입되며, 각 암호화 연산이 고유한 암호문을 생성하도록 보장하여 보안을 강화합니다.

샤미르 비밀 공유(SSS) 방식처럼 비밀 공유 전에 복호화 키가 있어야 하는 기존 복호화 키 관리 방식과 관련된 중앙 집중화 위험을 완화하기 위해 분산 키 생성(DKG) 방식이 채택되었습니다. 이 방식은 모든 참여자가 분산된 방식으로 복호화 키를 생성할 수 있는 메커니즘을 제공하여, 공개 전에 어느 누구도 완전한 키를 소유하지 못하게 합니다.

대부분의 DKG 프로토콜은 검증 가능한 비밀 공유(VSS) 방식을 채택하여 신뢰할 수 있는 당사자의 필요성을 제거합니다. VSS는 참여자 간의 상호작용을 통해 공유 유효성을 검증하도록 요구합니다. 이 프로세스는 투표 시 필요에 따라 복호화 키 공유에 대한 ZK 증명을 검증하는 방식으로 대체됩니다.

DKG는 당사자 간 키 공유 교환의 필요성을 없애지만, 제안서 작성 과정에서 암호화 키 공유를 공개해야 합니다. 결정론적 KDF를 사용하면 참여자는 상호 작용 과정을 피할 수 있으며, 제안서 작성자는 최종 암호화 키를 비동기적이고 독립적으로 집계할 수 있습니다.

4. 보안 고려 사항 및 제한 사항

이 프로토콜에는 고려해야 할 몇 가지 보안 위험과 제한 사항이 내재되어 있습니다.

• 신뢰할 수 있는 설정. Groth16을 zk-SNARK 검증 시스템으로 사용하는 경우, 회로별 신뢰할 수 있는 설정이 필요하며, 이를 올바르게 수행해야 합니다.

• 개인 키/서명 유출. 키 파생 ECDSA 서명을 비공개로 유지하는 것이 필수적입니다. babyJubJub 키 쌍은 이 서명에서 직접 파생되므로, 서명 유출 시 사용자가 속한 다중 서명 시스템이 피싱/스팸 공격에 취약해집니다.

• 제안 선행 실행. 제안 챌린지는 제안 내용에서 결정적으로 도출되지만, 동일한 제안으로 제안 생성을 선행 실행하는 것은 여전히 가능합니다. 이는 보안에 직접적인 영향을 미치지는 않지만, 유의해야 합니다.

• 참여자 제거 교착 상태. 제거될 참여자가 투표하지 않으면 (참가자에게는 당연한 일이지만), 제거 제안은 만료되고 해당 참여자는 다중 서명 회원으로 남게 됩니다. 이러한 제안에 대해 공개적으로 투표하는 것이 해결책이 될 수 있습니다.

• 참여자 목록 수정. 활성(진행 중인) 제안이 있을 때마다 다중 서명에서 참여자를 추가하거나 제거하는 것은 어렵습니다. 이로 인해 암호화 체계에 사용되는 키의 불일치가 발생할 수 있습니다. 가능한 해결책은 이러한 제안을 추적하고 다른 진행 중인 제안이 없을 때만 생성되도록 허용하는 것입니다.

• 마지막 투표자의 이점. 모든 복호화 키 공유가 알려지면 투표 복호화가 가능하므로, 마지막 참여자는 자신의 투표를 하기 전에 이전 투표를 재구성할 수 있습니다.

• 확장성. 투표 공개 및 제안 결과 계산의 복잡성은 참여자 수에 따라 선형적으로 증가합니다.

참고문헌

[1] Nicolas T. Courtois 및 Rebekah Mercer. 스텔스 주소 및 키 관리 기술
블록체인 시스템. 2017. url: https://www.scitepress.org/papers/2017/62700/62700.pdf .
[2] Neal Koblitz. 타원 곡선 암호 시스템. 1987. url: https://www.ams.org/journals/mcom/1987-48-177/S0025-5718-1987-0866109-5/S0025-5718-1987-0866109-5.pdf .