저자: 데이비드 웡
출처: https://www.cryptologie.net/posts/hash-based-signatures-part-i-one-time-signatures-ots/
램포트 서명
1979년 10월 18일, 레슬리 램포트는 일회성 서명 이라는 자신의 발명품을 발표했습니다 .
대부분의 서명 방식은 보안 증명을 위해 단방향 함수, 일반적으로 해시 함수에 의존합니다. 램포트 방식의 장점은 서명이 이러한 단방향 함수의 보안에만 의존한다는 점입니다.
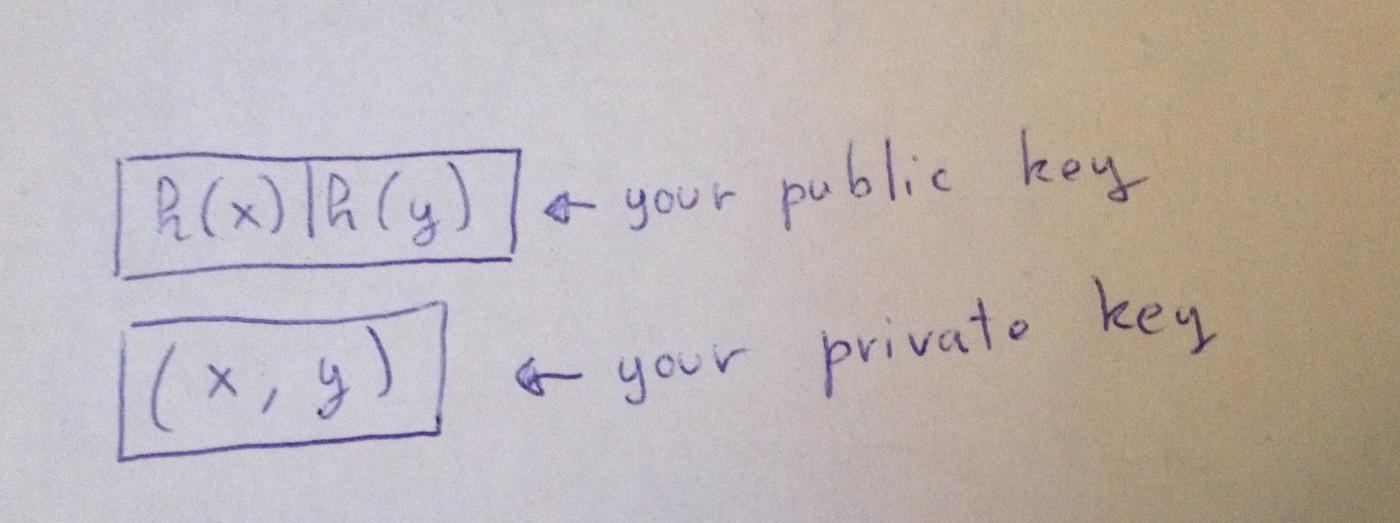
(H(x) | H(y)) <-- 你的公钥(x, y) <-- 你的私钥램포트 방식은 매우 간단합니다. 우선, x 와 y 는 모두 정수입니다. 단일 비트를 서명할 때:
- 이 비트의 값이
0이면x - 이 비트의 값이
1이면y
아주 간단하죠? 하지만 당연히 같은 공개키로 여러 번 서명할 수는 없습니다.
그렇다면 여러 비트를 서명해야 하는 경우는 어떻게 해야 할까요? 먼저 서명하려는 메시지를 해시 처리할 수 있습니다. 예를 들어 SHA-256 해시 함수를 사용하면 됩니다. (이 함수의 출력 길이는 예측 가능하므로 서명해야 할 데이터의 길이를 고정할 수 있습니다.)
자, (256비트를 서명하려면) 256개의 개인 키 쌍이 필요합니다.
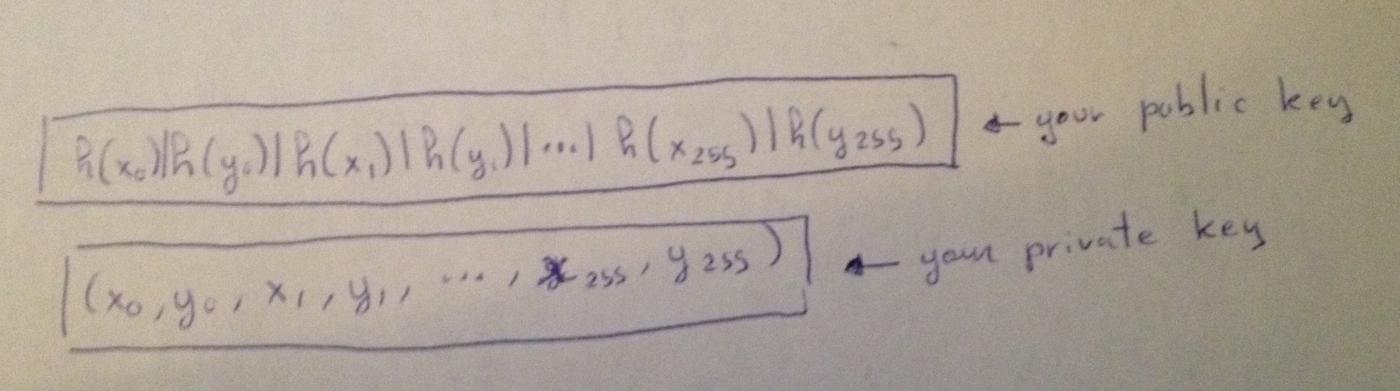
(H(x_0) | H(y_0) | H(x_1) | H(y_1) | ... | H(x_255) | H(y_255)) <-- 你的公钥(x_0, y_0, x_1, y_1, ... x_255, y_255) <-- 你的私钥예를 들어, 100110 에 서명하려면 (y_0, x_1, x_2, y_3, y_4, x_5) 를 게시해야 합니다.
윈터니츠 OTS (WOTS)
램포트의 논문이 발표된 지 몇 달 후, 스탠포드 대학교 수학과의 로버트 윈터니츠는 $h(x) | h(y)$ 대신 $h^w(x)$를 발표할 수 있다고 제안했습니다.
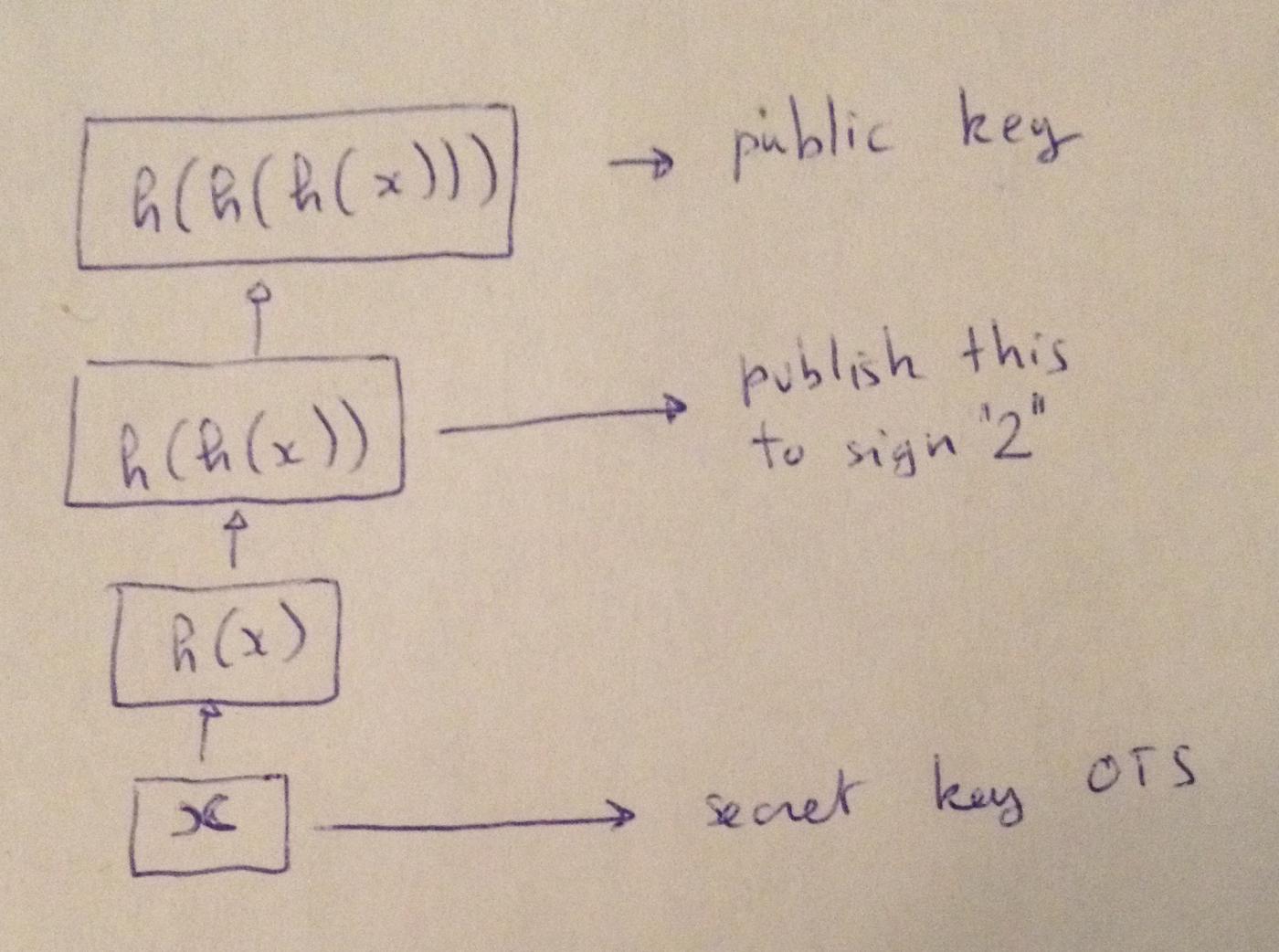
(역자 주: 일회용 서명을 위한 개인 키로 정수 x 사용합니다. H(x) 사용하여 1 숫자에 서명하고, H(H(x)) 사용하여 2 숫자에 서명하는 식으로 진행합니다. 서명하려는 가장 큰 숫자가 n 이라고 가정하면, x n + 1 번 연속으로 해싱한 결과가 공개 키가 됩니다.)
예를 들어, $w = 16$을 선택하고 $h^{16}(x)$을 공개 키로 게시하면 $x$만 개인 키로 저장하면 됩니다. 이제 이진수 $1010$(십진수로 $9$)에 서명하려면 $h^{9}(x)$만 게시하면 됩니다.
이제 또 다른 문제는 악의적인 사람이 이 서명을 보고 해시할 수 있다는 것입니다. 예를 들어, 다시 해시하면 $h^{10}(x)$를 얻을 수 있는데, 이는 이진수 1010 (또는 십진수 10 )에 대한 유효한 서명을 위조하는 것입니다.
윈터니츠의 일회성 서명의 변형
훨씬 후인 2011년에 Buchmann 등이 Winternitz 일회용 서명에 대한 업데이트를 발표하면서 키를 인수로 받는 함수 계열을 도입하는 변형을 제시했습니다. 이 함수는 일종의 "메시지 인증 코드(MAC)"라고 생각할 수 있습니다.
이제 여러분의 개인 키는 MAC에서 사용될 키들의 집합이 되고, 메시지는 이 MAC을 몇 번 반복할지 결정합니다. 이는 이전 반복의 결과가 함수에 사용된 키를 대체하고, 함수에 제공하는 입력값이 항상 동일하며 공개되어 있다는 점에서 특별한 반복 방식입니다. 예를 들어 보겠습니다.
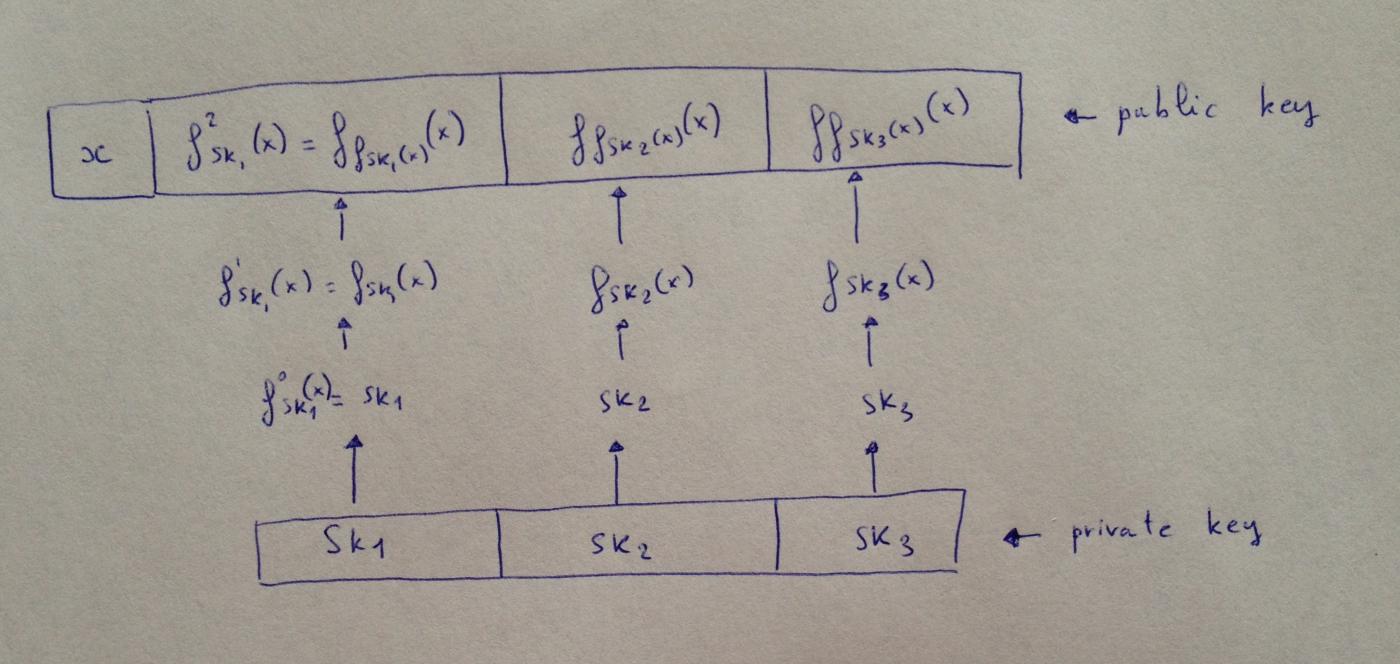
(역자 주: 그림에서 보는 바와 같이, 먼저 키 sk_i 생성됩니다. 값 0 에 대한 서명은 sk_i 자체입니다. 그 후, 1 이상의 값에 서명하기 위해, 모든 sk_i 에 대해 sk_i 매개변수로, x 입력으로 하여 함수를 한 번 실행합니다. 이것이 한 번의 반복입니다. 이 반복에서 얻은 값은 다음 반복의 매개변수가 됩니다. x 는 공개 키의 일부이며 항상 공개됩니다.)
서명해야 할 메시지는 이진수 1011 이며, 이는 십진수 11 입니다. W-OTS 변형이 3 진법을 사용한다고 가정합니다(실제로 어떤 w 이든 사용할 수 있습니다). 따라서 메시지를 삼진수 $M = (M_0, M_1, M_2) = (1, 0, 2)$로 변환합니다.
이 메시지에 서명하려면 마지막 항목이 $f^2_{sk_3}(x) = f_{f_{sk_3}(x)}(x))$인 $(f_{sk_1}(x), sk_2, f^2_{sk_3}(x))$만 게시하면 됩니다.
여기서 언급하지 않은 사항이 하나 있는데, 저희 메시지에는 체크섬이 있으며 이 체크섬에도 서명이 필요합니다. 따라서 $(M_2 = 2)$의 서명이 이미 공개 키에 노출되어 있더라도 상관없습니다.
직관적으로 생각해보면 공개 키에 반복 과정을 추가하면 보안이 향상될 수 있을 것 같습니다.
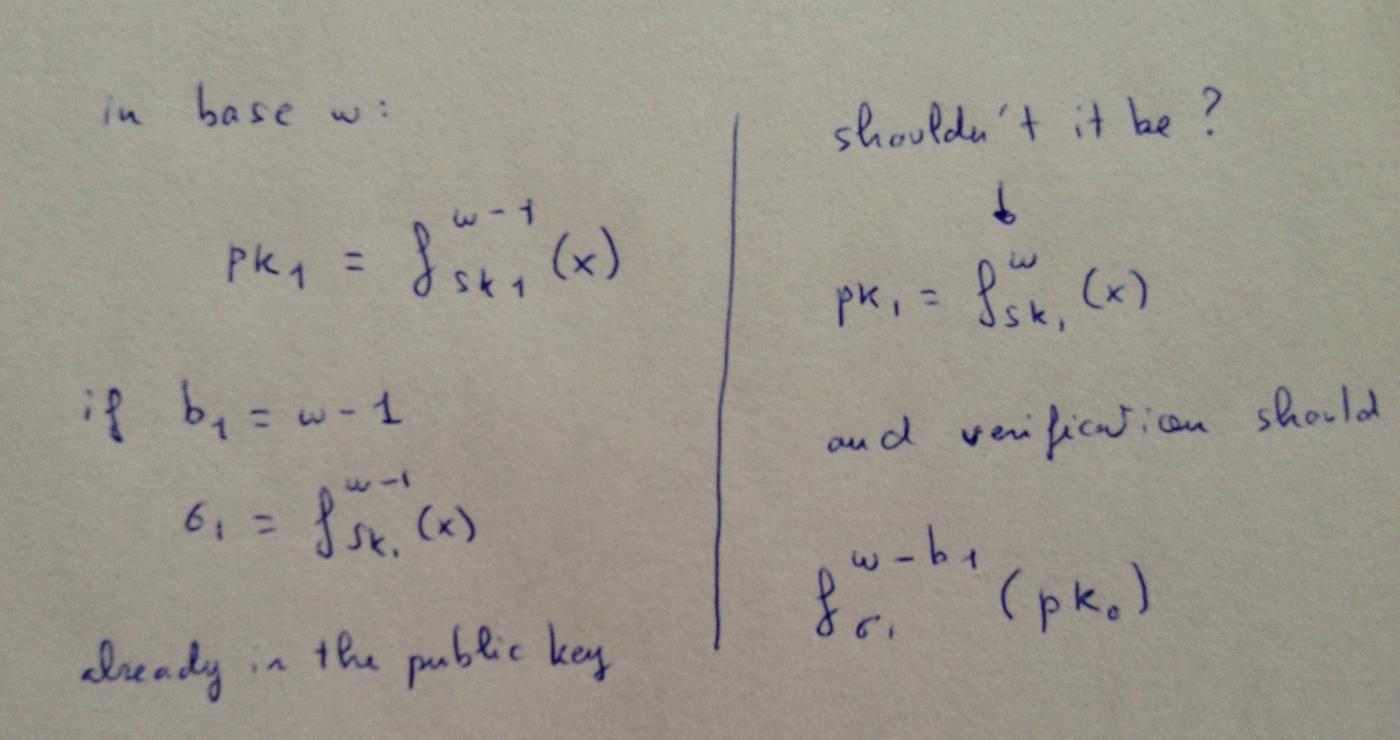
다음은 안드레스 훌싱이 이 주제에 대한 강연 에서 제 질문에 답한 내용입니다.
왜 그럴까요? 첫 번째 비트를 예로 들면, 체크섬은 0이 됩니다. 따라서 이 메시지에 서명하려면 공개 키 요소의 역상만 알면 됩니다. 이 방식이 안전하려면 보안 매개변수에 따라 난이도가 기하급수적으로 증가해야 합니다. 공격자가 두 값에 대해 해시 함수를 역으로 수행하거나, 동일한 값에 대해 두 번 역으로 수행할 수 있도록 요구하는 것은 공격 복잡성을 2배로만 증가시킬 뿐입니다. 이는 방식의 보안을 크게 향상시키지 않습니다. 비트 보안 관점에서 보면, 실행 시간을 두 배로 늘리는 대가로 보안이 단 1비트만 더 향상될 뿐입니다.
(역자 주: "비트 보안"은 시스템을 뚫는 데 필요한 무차별 대입 검색 횟수를 나타냅니다. 예를 들어, "80비트 보안"은 $2^{80}$번의 검색이 필요하다는 의미입니다.)
윈터니츠 OTS+ (WOTS+)
W-OTS+ 방식에 대해서는 특별히 언급할 내용이 많지 않습니다. 앞서 언급한 변종이 등장한 지 2년 후, 훌싱은 서명 크기를 줄이고 보안을 강화한 업그레이드 버전을 독자적으로 발표했습니다. 이 업그레이드 버전은 키를 매개변수로 받는 함수들 외에도 체이닝 함수를 사용합니다. 업데이트된 방식에서는 각 반복마다 키는 동일하게 유지되며, 입력값만 이전 반복의 출력값이 됩니다. 또한, 이전 출력값에 단방향 함수를 적용하기 전에 임의의 값(또는 "마스크")과 XOR 연산을 수행합니다.
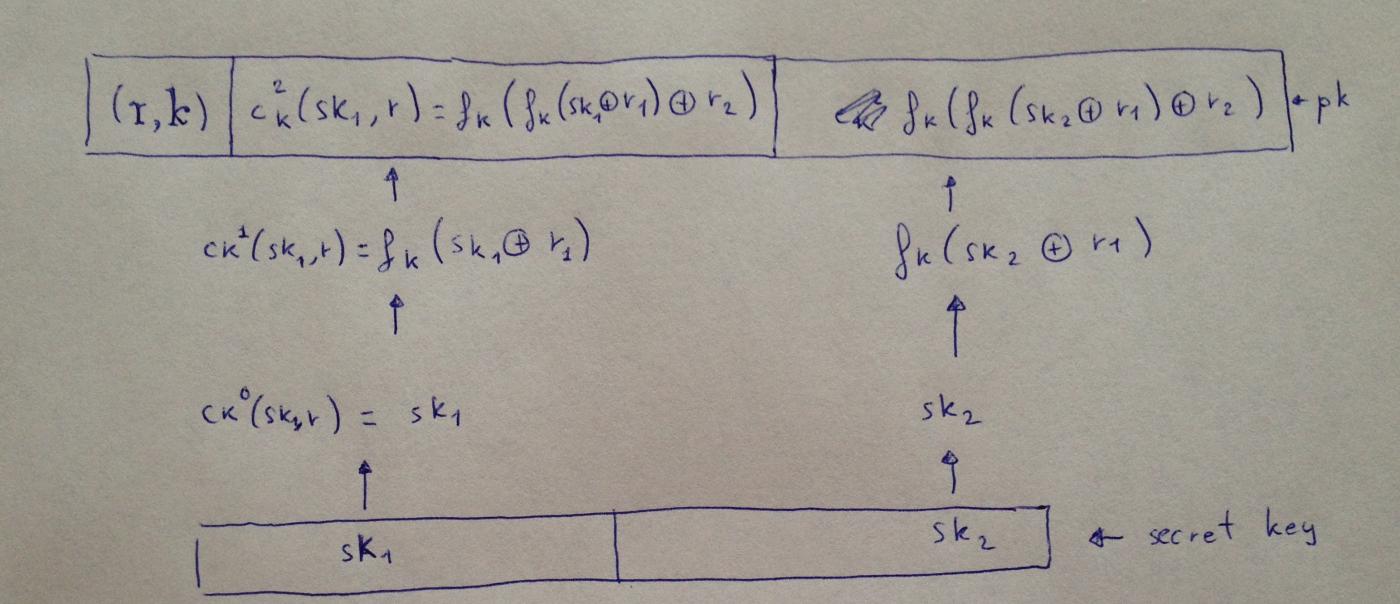
훌싱이 제시한 축약 서명에 대한 정확한 설명:
WOTS+는 더 짧은 해시 함수를 사용할 수 있기 때문에 서명 크기를 줄일 수 있습니다(동일한 보안 수준 또는 더 긴 해시 체인을 사용하는 다른 WOTS 변형과 비교). 즉, 모든 WOTS 변형에 동일한 해시 함수, 동일한 출력 길이 및 동일한 Winternitz 매개변수
w사용하는 경우 WOTS+는 다른 변형보다 더 높은 보안 수준을 달성할 수 있습니다. 이는 예를 들어 128비트 해시 함수를 사용하려는 경우 중요합니다. 원래 WOTS는 해시 함수가 충돌 방지 기능을 갖춰야 했지만, 2011년 변형과 WOTS+는 의사 난수 함수/2차 역상 저항 해시 함수만 요구한다는 점을 기억하십시오. 이 경우 원래 WOTS는 64비트의 보안 수준만 달성할 수 있으며, 이는 안전하지 않다고 볼 수 있습니다. 2011년 제안과 WOTS+는128 - f(m, w)비트의 보안 수준을 달성할 수 있습니다. 후자 두 가지의 차이점에 대해 설명하자면, WOTS-2011에서는f(m, w)w에 비례하여 선형적으로 증가합니다. WOTS+에서f(m, w)w에 따라 선형적으로 증가하며, 로그 함수적 성장을 보인다.
기타 OTS
오늘의 블로그 포스팅은 여기까지입니다! 하지만 일회용 서명 방식은 이 외에도 많이 있습니다. 관심 있으시면 아래 목록을 참고하세요. 이 중 일부는 일회용 서명을 넘어 소량으로 재사용할 수 있는 방식입니다. 따라서 이러한 방식을 "소량 재사용 서명 방식(Few-Time Signature Schemes, FTS)"이라고 부를 수 있습니다.
- 1994년, 블라이헨바허-마우러 OTS
- 2001년, BiBa OTS
- 2002년, 말
- 2014, HORST (나무가 있는 말)
현재까지는 적용 분야가 해시 함수 기반 서명으로 좁혀진 것으로 보입니다. 이는 양자 후 보안에 현재 권장되는 서명 방식이기 때문입니다. 몇 달 전에 발표된 " 양자 후 암호화에 대한 예비 권고 사항 "을 참조하십시오.