전문
이전 부분 에서 우리는 기본적으로 zk-SNARK의 수학적 및 코딩 기반 에 대해 배웠습니다. 이제 저는 여러분이 zk-SNARK 이면의 기술을 더 깊이 이해할 수 있도록 더욱 새롭고 복잡한 개념을 계속해서 탐구하겠습니다!
산술 회로(산술 회로)
산술 회로의 개념
산술 회로는 DAG(방향성 비순환 그래프) , 즉 간단히 말하면 다음을 포함하는 방향성 비순환 그래프입니다.
- 노드는 덧셈과 곱셈 게이트 역할을 합니다.
- 모서리는 유한 필드 Fp에 설정된 도체 를 나타냅니다 . 와이어는 한 포트의 출력을 다른 포트의 입력에 연결합니다. 각 포트에는 2개의 입력과 1개의 출력이 있습니다.
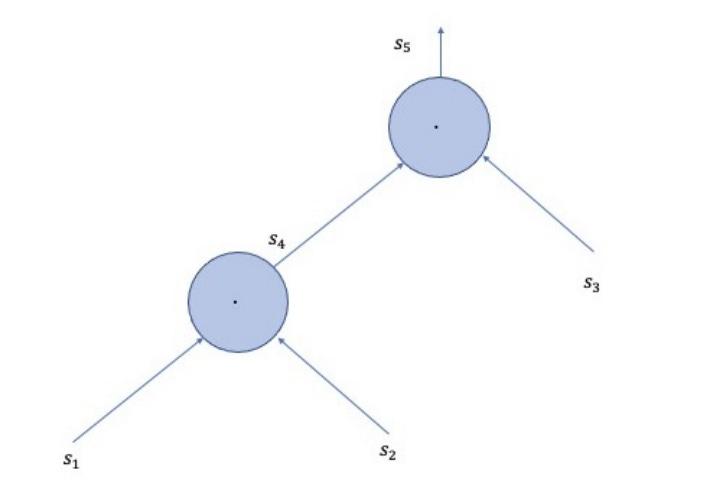
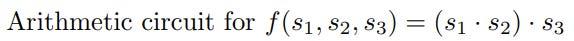
산술 회로는 최종 출력으로 끝납니다. 위 그림은 데이터가 어떻게 처리되고 각 게이트를 통과하여 최종 결과를 생성하는지 볼 수 있는 산술 회로의 예를 보여줍니다.
산술 회로는 zk-SNARK가 정보를 공개하지 않고 계산을 처리하고 증명하는 방법을 알려줍니다. 산술 회로는 체계적으로 배열된 산술 연산을 포함하는 다이어그램으로 설명할 수 있습니다.
산술 회로의 작동
위의 그림을 고려하면 산술 회로를 통해 다음을 계산할 수 있습니다.
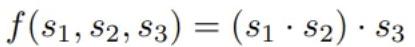
위 이미지를 보면 이 프로세스는 s1 과 s2를 입력으로 받고 s4를 출력으로 생성하는 첫 번째 커널 게이트 에서 시작되는 것을 알 수 있습니다. 다음으로, s4 와 s3은 두 번째 커널 게이트 에 공급되어 최종 출력 s5를 생성합니다.
m- 포트, n- 와이어 회로의 경우 이를 결정할 수 있습니다.
증인 s = (s1, s2, s3,…, sn)
각 게이트의 입력과 출력이 게이트의 동작에 의해 결정된 제약 조건을 만족하도록 회로의 n 와이어에 할당합니다.
M 포트, N 와이어 산술 회로가 증인의 관계를 결정합니다.
s = (s1, s2, …, sn)
그렇게 끊임없이

그 다음에
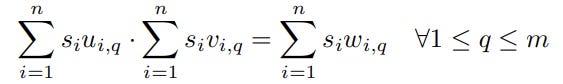
위의 제약 조건은 m 개의 랭크-1 제약 조건 집합에 속하며, 그 목적은 산술 회로에서 곱셈기 게이트의 입력과 출력 간의 관계를 시뮬레이션하는 것입니다.
특정 순위 1 제약 조건의 예는 Eq입니다.
s1 . s2 – s3 = 0.
이 방정식은 회로의 곱셈기 게이트를 설명합니다. 이 게이트는 두 개의 입력 s1 과 s2를 사용하여 출력 s3을 생성합니다. 따라서 방정식이 충족되려면 s1 과 s2 의 곱이 s3 과 같아야 합니다.
이와 같은 m개의 랭크-1 제약 조건 세트는 이차 산술 프로그램 으로 일반화될 수 있습니다.
QAP는 전체 회로를 다시 렌더링하지 않고도 연산을 더 쉽게 확인할 수 있는 형태로 산술 회로를 변환하고 줄이는 도구입니다.
이차 산술 프로그램
zk-SNARK 의 핵심은 QAP(Quadratic Arithmetic Programs )에 있습니다. QAP는 덧셈과 곱셈 게이트를 포함한 모든 산술 회로를 나타낼 수 있습니다. QAP를 기반으로 증명자는 해당 값이나 프로그램의 내부 동작에 대해 아무것도 공개하지 않고도 입력 값을 알고 있다는 증거를 생성할 수 있습니다.
zk-SNARK 연구원 Eran Tromer는 다음과 같이 기본 수학적 원리로부터 zk-SNARK 구성 프로세스를 도출했습니다.

위의 단계는 두 부분으로 나눌 수 있습니다. 이 기사에서는 프로세스의 "전반부"에 대해 자세히 설명합니다. 프로세스의 "전반"은 "계산" 부터 "QAP" 까지의 단계로 간주될 수 있습니다. 이는 초기 계산이 zk-SNARK를 설정하는 데 사용할 수 있는 수학적 형식으로 변환되는 부분입니다.
다음과 같이 이해하기 쉽게 설명하겠습니다.
계산 문제에 zk-SNARK를 사용하려면 먼저 문제를 적절한 "형식" 으로 변환해야 합니다. 이 형식을 QAP 또는 " 이차 산술 프로그램 "이라고 합니다.
문제를 QAP 로 변환한 후에는 몇 가지 특정 입력을 통해 문제 해결을 진행합니다. 찾아낸 해결책을 ' 간증 '이라고 합니다. 이는 마치 우리가 퍼즐을 풀고 답을 아는 것과 같습니다.
이제 답을 얻었으므로 답을 공개하지 않고도 답을 알고 있음을 증명할 수 있는 방법을 만들어야 합니다. 이 프로세스는 " 비공개 증거 "를 생성합니다. 즉, 말하지 않고도 답을 알고 있음을 증명할 수 있다는 의미입니다.
마지막으로, 다른 사람이 별도의 프로세스를 사용하여 우리가 만든 증거를 확인하고, 실제로 답이 무엇인지 알지 못한 채 우리가 실제로 답을 알고 있는지 확인할 수 있습니다!
예를 들어 다음과 같은 방정식이 있습니다.
x**3 + x + 5 == 37 (권장 답변은 3입니다)
우리는 다음과 같이 간단한 컴퓨터 프로그램을 작성함으로써 해를 공개할 필요 없이 위 수학 방정식의 해를 알고 있음을 증명할 것입니다.

qevel 함수는 방정식 x**3 + x + 5 의 값을 계산합니다. 숫자 3을 x에 대입하면 함수는 우리가 원하는 결과인 35를 반환합니다.
그러나 이 경우에는 프로그래밍 언어의 한계를 보게 됩니다. 이 언어는 기본 산술 연산(+, -, *, /) 과 고정 지수를 사용한 거듭제곱(x**y가 아닌 x**7) 만 지원합니다. 유한 순환 그룹 산술에서는 모듈로 또는 비교를 직접 수행할 수 있는 효율적인 방법이 없기 때문에 나머지(%) 또는 비교(>, <, ≤, ≥)를 사용한 나눗셈을 지원하지 않습니다.
여기서 해결책은 이 언어를 확장하여 나머지 나누기 및 비교 와 같은 추가 작업을 지원할 수 있다는 것입니다.
예를 들어:
x < 5인 경우: y = 7; 그렇지 않으면: y = 9
이를 산술로 변환하여:
y = 7 * (x < 5) + 9 * (x >= 5)
opcode를 vbuterin 이 구현한 zk-SNARK 에 사용 가능한 형식으로 변환하는 데 사용할 수 있는 컴파일러 를 참조할 수 있습니다(교육 목적으로만 사용되며 실제로 zk-SNARK 용 QAP를 생성할 준비가 아직 되지 않음).
평탄화
이러한 형태 의 QAP 로 변환하는 첫 번째 단계는 "평탄화" 단계입니다. 간단히 말해서 프로그래밍 코드를 더 간단하게 변환하는 단계입니다. 각 줄은 하나의 기본 작업만 수행합니다.
위의 예에서 초기 컴퓨터 프로그램에는 복잡한 수학적 표현이 있습니다. " 평탄화" 프로세스는 이 표현식을 작은 부분으로 분할하고 각 부분은 단 하나의 간단한 계산을 수행합니다.
Sym_1 = x * x
x 자체를 곱하여 Sym_1 이라는 중간 값을 생성합니다.
y = Sym_1 * x
그런 다음 정확한 계산 x^3 에 따라 중간 값 Sym_1 에 x를 다시 곱하여 y를 생성합니다.
Sym_2 = y + x
x 로 방금 계산한 y를 더하세요.
~아웃 = Sym_2 + 5
마지막으로 Sym_2 에 5를 추가하여 최종 결과를 얻고, 출력 앞에 ~를 추가하여 이것이 프로그램의 최종 결과임을 나타냅니다.
매우 이해하기 쉽습니다! 이 "평탄화" 프로세스는 zk-SNARK 에서 처리할 코드를 준비하는 데 도움이 됩니다. 왜냐하면 zk-SNARK는 작업할 수 있는 수학적 형식으로 쉽게 변환할 수 있는 간단한 형식의 프로그래밍 코드를 요구하기 때문입니다.
R1CS로 가는 문
다음으로 일련의 계산을 수행하여 (랭크-1 제약 시스템) , 약어로 R1CS라고 하는 좀 더 복잡한 형태로 변환합니다.
R1CS는 세 벡터 (a, b, c) 로 구성된 그룹의 시퀀스이고 R1CS 에 대한 해는 벡터 s 입니다. 여기서 s는 다음 방정식을 충족해야 합니다.
s. 처럼 . b – s. c = 0
출력 값이 두 입력 값의 올바른 곱인지 확인합니다. 이러한 조건이 모두 충족되면 시스템에 대한 정확한 솔루션 벡터를 갖게 됩니다.
R1CS를 더 잘 이해하기 위해 아래 이미지를 볼 수 있습니다.
먼저, 시스템에서 사용되는 변수를 정의하고, 다음과 같이 변수를 매핑하는 단계를 제공하겠습니다.
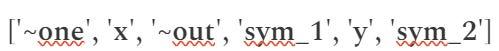
- “~one” (첫 번째 아래 첨자는 숫자 1을 나타냄)
- “x” (입력 변수)
- “~out” (출력 변수)
- “sym_1”, “y”, “sym_2” (중간 변수)
벡터 "s" 에는 정의된 순서대로 이러한 모든 변수에 대한 값이 포함됩니다.
# 첫 번째 게이트 ( x * x 곱셈)에 대한 트리플을 (a, b, c) 에 제공합니다.

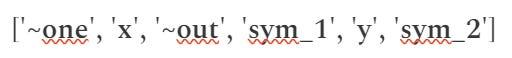
- 벡터 a 와 b는 모두 [0, 1, 0, 0, 0, 0] 값을 포함합니다. 각 벡터의 두 번째 위치에 있는 숫자 1은 변수 x 의 값이 계산에 사용됨을 나타냅니다. 특히, a 와 b 모두 위치 x 에 가중치를 두기 때문에 이 값은 자체적으로 곱해집니다.
- 벡터 c 의 값은 [0, 0, 0, 1, 0, 0] 이며 네 번째 위치에 숫자 1이 있습니다. 이는 a 와 b 에서 계산된 값이 벡터 s 의 변수 Sym_1 과 비교됨을 나타냅니다.
a = [0, 1, 0, 0, 0, 0] : 변수 " x "가 계산에 참여하도록 지정합니다.
b = [0, 1, 0, 0, 0, 0] : " x "가 자체적으로 곱해지도록 다시 지정합니다.
c = [0, 0, 0, 1, 0, 0] : 결과는 변수 “ sym_1 ”에 저장됩니다.
" x = 3 "인 경우 계산은 " 3 * 3 = 9" 가 되며 "sym_1 = x * x" 제약 조건을 충족합니다.
#다음은 두 번째 게이트 입니다(곱셈 Sym_1 * x 의 경우).

비슷한,
a = [0, 0, 0, 1, 0, 0] : " sym_1 "을 지정합니다( "x = 3"인 경우 9 ).
b = [0, 1, 0, 0, 0, 0] : " x "를 지정합니다( "x = 3"인 경우 3 ).
c = [0, 0, 0, 0, 1, 0] : 결과는 “ y ”에 저장됩니다.
계산은 " 9 * 3 = 27 "이며 제약 조건을 충족합니다.
#다음은 세 번째 게이트 입니다( x + y 추가용).

비슷한,
a = [0, 1, 0, 0, 1, 0] : "x" 및 "y" 지정
b = [1, 0, 0, 0, 0, 0] : 덧셈이 올바르게 수행되도록 "1" ( "~one"을 나타냄) 값을 사용합니다.
c = [0, 0, 0, 0, 0, 1] : 결과는 “sym_2” 에 저장됩니다.
계산은 "3 + 27 = 30" 이며 "sym_2 = x + y" 제약 조건을 충족합니다.
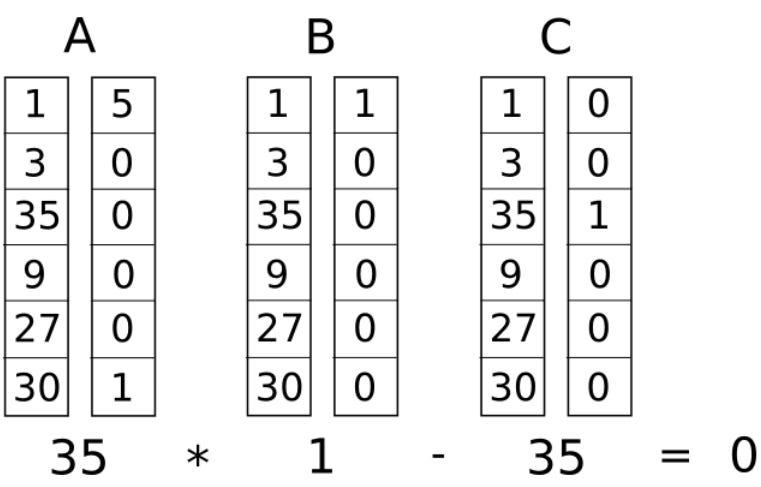
#마지막으로 네 번째 게이트 (추가를 위해 Sym_2 + 5 ):

비슷한,
a = [5, 0, 0, 0, 0, 1] : "~one" 의 " 5 " 값과 "sym_2" 의 " 1 " 값을 사용합니다.
b = [1, 0, 0, 0, 0, 0] : 다시 " ~one" 이므로 덧셈이 올바르게 수행됩니다.
c = [0, 0, 1, 0, 0, 0] : 결과는 " ~out" 에 저장됩니다.
계산은 "30 + (5*1) = 35" 이며, 이는 "~out = Sym_2 + 5" 제약 조건을 충족합니다.
세 개의 열 A, B , C 는 벡터 " a" , " b" 및 "c "에 해당합니다. C 열 하단의 숫자 “ 35 ”가 최종 결과( “~out”) 입니다.
(s . a) * (s . b) 및 (s . c)를 비교하면 동일해야 합니다(차이는 0이어야 함).
이 시점에서 벡터 "s" 에는 다음 값이 포함됩니다.
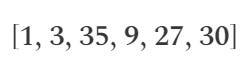
- 1: 상수 1을 나타내기 위해 항상 1인 더미 변수 ~one 의 값입니다.
- 3: 입력 변수 x 의 값입니다.
- 35: 이것은 원하는 값이며 프로그램의 최종 결과입니다 (변수 ~out) .
- 9: x * x 의 결과, Sym_1 에 저장됨.
- 27: Sym_1 * x 의 결과, y 에 저장됨.
- 30: y + x 의 결과, Sym_2 에 저장됨.
마지막으로 완전한 R1CS는 아래와 같이 구성됩니다.

R1CS에서 QAP로
다음 단계는 이 R1CS를 QAP 형식으로 변환하는 것입니다. 단, R1CS 와 같이 벡터 와 내적을 사용하는 대신

QAP는 테스트 프로세스를 더 쉽게 만드는 특별한 수학적 속성을 갖고 있기 때문에 " 다항식"을 사용합니다.
라그랑주 보간법은 일련의 알려진 점을 통과 하는 곡선(다항식)을 그리는 방법입니다. 특정 수의 점이 있고 해당 점 모두에 닿는 곡선 (다항식) 을 원하는 경우 라그랑주 보간법을 사용하면 해당 곡선을 찾을 수 있습니다.
예를 들어, (1, 3), (2, 2) 및 (3, 4)를 통과하는 다항식을 원한다고 가정합니다. (1, 3), (2, 0) 및 (3, 0)을 통과하는 다항식을 만드는 것으로 시작합니다.
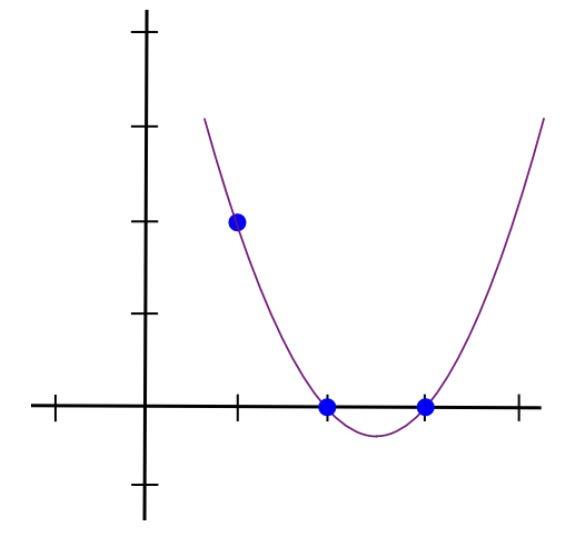
이를 수행하는 간단한 방법은 (x-2) 와 (x-3) 의 곱을 취하는 것입니다. 이 함수는 x=1에서 상승하고 x=2 및 x=3 에서 수평 축을 자르는 곡선 모양을 갖습니다.
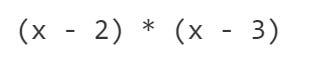
아래:
이제 x=1 의 높이가 정확하도록 " 조정" 하면 됩니다.
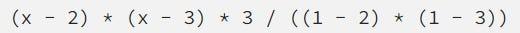
그러면 다항식이 만들어지고 그래프는 아래와 같이 표시됩니다.

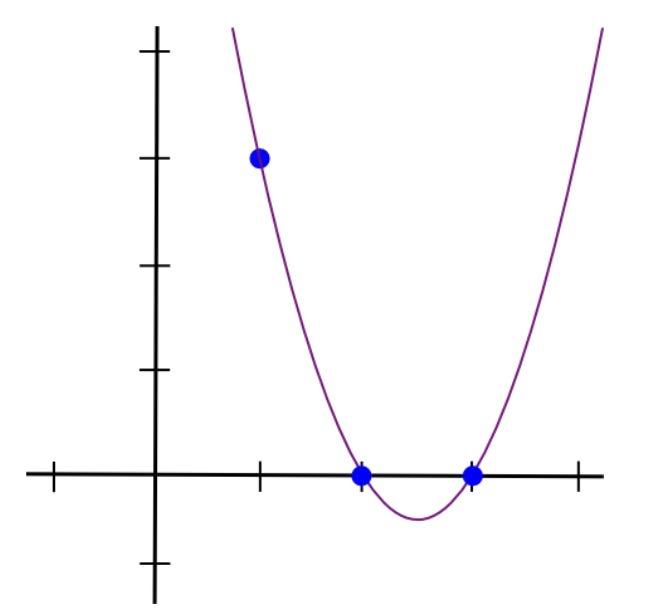
그런 다음 나머지 두 점에 대해 동일한 작업을 수행하고 두 개의 다항식을 더 얻고 세 개를 모두 더하면 다음을 얻습니다.


원래 알고리즘은 계산하는 데 O(n^3) 시간이 걸립니다. 왜냐하면 n 점 각각에 다항식을 곱하는 데 O(n^2)가 필요하기 때문입니다. 그러나 더 똑똑하게 생각하면 이 시간을 O(n^2) 로 줄일 수 있습니다.
FFT 변환과 같은 알고리즘을 적용하면 계산 시간을 더욱 빠르게 줄일 수 있으며 이는 수천 개의 게이트가 있는 zk-SNARK 와 같은 애플리케이션에서 중요합니다.
각 벡터 a 의 첫 번째 값을 취하여 R1CS를 변환하기 위해 라그랑주 보간을 적용한 다음 이 보간을 사용하여 각 벡터에 대한 다항식을 생성하므로 인덱스 특정 숫자에서 다항식을 평가할 때 다음의 첫 번째 값을 얻습니다. 해당 벡터.
벡터 b 와 c 의 첫 번째 값에 대해 동일한 작업을 수행한 다음 이 방법을 각 벡터의 다음 요소에 차례로 적용합니다.
우리는 아래와 같은 결과를 얻게 될 것입니다:

알고리즘은 일련의 증가하는 계수를 사용하여 다항식을 생성합니다.
이 다항식은 고려 중인 QAP(Quadratic Arithmetic Program) 버전에 대한 매개변수의 일부입니다.
이러한 매개변수 설정은 zk-SNARK 로 검증된 각 기능에 대해 한 번만 수행하면 된다는 점에 유의해야 합니다. 일단 설정되면 재사용이 가능합니다.
x=1 에서 모든 다항식을 평가할 때 모든 계수를 더하기만 하면 되기 때문에 프로세스가 매우 간단합니다( k 의 모든 값에 대해 1^k 는 항상 1 이므로). 다음 결과를 얻게 됩니다.

- x = 1에서 평가될 때 다항식 A는 두 번째 결과인 1을 제외하고 모든 결과가 0입니다.
- x = 1에서 평가할 때 다항식 B는 두 번째 결과인 1을 제외하고 모든 결과를 0으로 제공합니다.
- x = 1에서 평가될 때 다항식 C는 네 번째 결과인 1을 제외하고 모든 결과가 0입니다.
여기에 있는 것은 위에서 만든 첫 번째 논리 게이트 와 정확히 동일한 벡터 삼중항(a, b, c) 입니다.
기사 출처: 팀 기술/연구 AlphaTrue
참고 출처:
- Chen, T., Lu, H., Kunpittaya, T., & Luo, A. (2022). zk-snarks에 대한 리뷰입니다. arXiv 사전 인쇄 arXiv:2202.06877 . https://arxiv.org/pdf/2202.06877.pdf
- https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649
- https://eprint.iacr.org/2012/215.pd