Truyền khối/blob nhanh hơn trong Ethereum
Xin cảm ơn @n1shantd , @ppopth và Ben Berger đã thảo luận và phản hồi về bài viết này và @dankrad đã có nhiều cuộc thảo luận hữu ích.
Tóm tắt
Chúng tôi đề xuất một thay đổi về cách chúng tôi phát và chuyển các khối và blob trong mạng P2P, bằng cách sử dụng mã hóa mạng tuyến tính ngẫu nhiên. Chúng tôi chỉ ra rằng về mặt lý thuyết, chúng tôi có thể phân phối khối tiêu thụ 5% băng thông và với 57% số lần nhảy mạng (do đó giảm một nửa độ trễ cho mỗi tin nhắn) so với thời gian thực hiện gossipsub hiện tại. Chúng tôi cung cấp các điểm chuẩn cụ thể cho chi phí tính toán.
Giới thiệu
Cơ chế phân phối khối hiện tại của gossipsub hoạt động như sau. Người đề xuất chọn một tập hợp con ngẫu nhiên (gọi là Mesh ) gồm D=8 đối tác trong số tất cả các đối tác của mình và phát khối của mình cho họ. Mỗi đối tác nhận được một khối thực hiện một số xác thực sơ bộ rất nhanh: chủ yếu là xác minh chữ ký, nhưng quan trọng nhất là không bao gồm quá trình chuyển đổi trạng thái hoặc thực hiện giao dịch. Sau khi xác thực nhanh này, đối tác phát lại khối của mình cho D đối tác khác. Có hai hậu quả tức thời từ thiết kế như vậy:
- Mỗi lần nhảy sẽ thêm ít nhất độ trễ sau: một lần chuyển khối đầy đủ từ một đối tác này sang đối tác tiếp theo (bao gồm cả độ trễ ping mạng, về cơ bản là không phụ thuộc vào băng thông, cộng với việc chuyển toàn bộ khối, bị giới hạn bởi băng thông).
- Các đối tác phát sóng một khối đầy đủ không cần thiết tới các đối tác khác đã nhận được khối đầy đủ.
Chúng tôi đề xuất sử dụng mã hóa mạng tuyến tính ngẫu nhiên (RLNC) ở cấp độ phát sóng. Với mã hóa này, người đề xuất sẽ chia khối thành N khối (ví dụ: N=10 cho tất cả các mô phỏng bên dưới) và thay vì gửi một khối đầy đủ cho ~8 đối tác, nó sẽ gửi một khối duy nhất cho ~40 đối tác (không phải một trong các khối ban đầu, mà là một tổ hợp tuyến tính ngẫu nhiên của chúng, xem bên dưới để biết các cân nhắc về quyền riêng tư). Các đối tác vẫn cần tải xuống một khối đầy đủ hoặc đúng hơn là N khối, nhưng họ có thể nhận chúng song song từ các đối tác khác nhau. Sau khi họ nhận được N khối này, mỗi khối là một tổ hợp tuyến tính ngẫu nhiên của các khối ban đầu tạo nên khối ban đầu, các đối tác cần giải một hệ phương trình tuyến tính để khôi phục toàn bộ khối.
Một bằng chứng về việc triển khai khái niệm làm nổi bật các con số sau
- Việc đề xuất một khối mất thêm 26ms bị giới hạn bởi CPU và có thể được song song hóa hoàn toàn trong vòng chưa đầy 2ms trên máy tính xách tay hiện đại (Apple M4 Pro)
- Việc xác minh từng khối mất 2,6ms.
- Giải mã toàn bộ khối mất 1,4ms.
- Với
10khối vàD=40, mỗi nút gửi một nửa dữ liệu so với gossipsub hiện tại và mạng phát một khối 100KB trong một nửa thời gian với lợi ích tăng dần theo kích thước khối.
Giao thức
Để có phần giới thiệu sâu hơn về mã hóa mạng và chúng tôi giới thiệu người đọc đến loc. cit. vàsách giáo khoa này . Ở đây chúng tôi đề cập đến các chi tiết triển khai tối thiểu cho các điểm chuẩn chứng minh khái niệm được trích dẫn ở trên. Trong trường hợp truyền khối (~110KB), độ trễ hoặc số lượng bước nhảy mạng chi phối thời gian truyền, trong khi trong trường hợp các thông điệp lớn như blob trong DAS đầy đủ, băng thông chi phối thời gian truyền.
Chúng tôi xem xét một trường hữu hạn \mathbb{F}_p F p có đặc tính nguyên tố. Trong ví dụ trên, chúng tôi chọn trường cơ sở vô hướng Ristretto được triển khai bởi thùng gỉ curve25519-dalek . Người đề xuất lấy một khối, là một lát byte mờ đục và diễn giải nó như một vectơ các phần tử trong \mathbb{F}_p F p . Một khối ethereum điển hình có kích thước khoảng B = 110KB B = 110 K B tại thời điểm viết bài, với điều kiện là mỗi vô hướng Ristretto chỉ cần ít hơn 32 byte để mã hóa, một khối cần khoảng B/32 = 3520 B / 32 = 3520 phần tử của \mathbb{F}_p F p . Chia thành N=10 khối, mỗi khối có thể được xem như một vectơ trong \mathbb{F}_p^{M} F M p , trong đó M \sim 352 M ∼ 352 . Khối do đó được xem như N N vectơ v_i \in \mathbb{F}^M_p v i ∈ F M p , i=1,...,N i = 1 , . . . , N . Người đề xuất chọn một tập hợp con của D\sim 40 D ∼ 40 đối tác ngẫu nhiên. Đối với mỗi đối tác như vậy, nó sẽ gửi một vectơ \mathbb{F}_p^M F M p cùng với một số thông tin bổ sung để xác thực các thông báo và ngăn chặn DOS trên mạng. Chúng tôi giải thích người đề xuất
Người đề xuất
Chúng ta sẽ sử dụng các cam kết Pedersen cho đường cong elliptic Ristretto E E như được triển khai bởi rust crate đã đề cập ở trên. Chúng ta giả sử rằng chúng ta đã chọn ngẫu nhiên một thiết lập đáng tin cậy gồm đủ các phần tử G_j \in E G j ∈ E , j = 1, ..., K j = 1 , . . . , K với K \gg M K ≫ M . Chúng ta chọn một cơ sở chuẩn \{e_j\}_{j=1}^M { e j } M j = 1 đối với \mathbb{F}_p^M F M p . Vì vậy, mỗi vectơ v_i v i có thể được viết duy nhất dưới dạng
$$ v_i = \sum_{j=1}^M a_{ij} e_j, $$
đối với một số số vô hướng a_{ij} \in \mathbb{F}_p a i j ∈ F p . Đối với mỗi vectơ v_i v i, chúng ta có một cam kết Pedersen
$$ C_i = \sum_{j=1}^M a_{ij}G_j \trong E. $$
Cuối cùng, đối với mỗi đối tác trong tập hợp con có kích thước D \sim 40 D ∼ 40, người đề xuất chọn ngẫu nhiên đồng đều một tập hợp các số vô hướng b_i b i , i=1, ...,N i = 1 , . . . , N và gửi thông tin sau cho đối tác
- Vectơ v = \sum_{i=1}^N b_i v_i \in \mathbb{F}_p^M v = ∑ N i = 1 b i v i ∈ F M p . Vectơ này có kích thước 32M 32 M byte và là nội dung của tin nhắn.
- N N cam kết C_i C i , i=1,...,N i = 1 , . . . , N . Đây là 32N 32 N byte.
- Các hệ số N N b_i b i , i=1, ...,N i = 1 , . . . , N . Đây là 32N 32 N byte.
- Chữ ký BLS cho hàm băm của N N cam kết C_1 || C_2 || ... || C_N C 1 | | C 2 | | . . . | | C N , đây là 96 96 byte.
Một thông điệp đã ký là tập hợp các phần tử 1–4 ở trên. Chúng ta thấy rằng có 64N \sim 640 64 N ∼ 640 byte bổ sung được gửi trên mỗi thông điệp dưới dạng sidecar.
Tiếp nhận đồng nghiệp
Khi một đối tác nhận được tin nhắn như trong phần trước, quá trình xác minh diễn ra như sau
- Nó xác minh rằng chữ ký là hợp lệ đối với người đề xuất và hàm băm của các cam kết nhận được.
- Nó ghi vectơ nhận v = \sum_{j=1}^M a_j e_j v = ∑ M j = 1 a j e j và sau đó tính toán cam kết Pedersen C = \sum_{j=1}^M a_j G_j C = ∑ M j = 1 a j G j .
- Các hệ số nhận được b_i b i là một yêu cầu rằng v = \sum_{i=1}^N b_i v_i v = ∑ N i = 1 b i v i . Đối tác tính toán C'= \sum_{i=1}^N b_i C_i C ′ = ∑ N i = 1 b i C i , sau đó xác minh rằng C = C' C = C ′ .
Các đối tác theo dõi các thông điệp mà họ đã nhận được, chẳng hạn như các vectơ w_i w i , i = 1,...,L i = 1 , . . . , L với L < N L < N . Chúng tạo ra một không gian con W \subset \mathbb{F}_p^M W ⊂ F M p . Khi chúng nhận được v v , trước tiên chúng kiểm tra xem vectơ này có nằm trong W W . Nếu có, thì chúng loại bỏ nó vì vectơ này đã là tổ hợp tuyến tính của các vectơ trước đó. Điểm mấu chốt của giao thức là điều này rất khó xảy ra (đối với các số ở trên, xác suất xảy ra điều này nhỏ hơn nhiều so với 2^{-256} 2 − 256 ). Hệ quả của điều này là khi nút đã nhận được N N thông điệp, thì nó biết rằng nó có thể khôi phục v_i v i ban đầu và do đó là khối, từ các thông điệp w_i w i , i=1,...,N i = 1 , . . . , N .
Lưu ý rằng chỉ cần một xác minh chữ ký, tất cả các tin nhắn đến đều có cùng cam kết C_i C i và cùng chữ ký trên cùng một tập hợp các cam kết, do đó, đối tác có thể lưu trữ đệm kết quả của xác minh hợp lệ đầu tiên.
Gửi đồng nghiệp
Các đối tác có thể gửi các khối cho các đối tác khác ngay khi họ nhận được một khối. Giả sử một nút giữ w_i w i , i=1,...,L i = 1 , . . . , L với L \leq N L ≤ N như trong phần trước. Một nút cũng theo dõi các hệ số vô hướng mà họ nhận được, do đó họ biết các khối mà họ giữ thỏa mãn
$$ w_i = \sum_{j=1}^N b_{ij} v_j \quad \forall i,$$
đối với một số số vô hướng b_{ij} \in \mathbb{F}_p b i j ∈ F p chúng lưu trong trạng thái nội bộ của chúng. Cuối cùng, các nút cũng giữ lại toàn bộ các cam kết C_i C i và chữ ký từ người đề xuất mà họ đã xác thực khi họ xác thực khối đầu tiên họ nhận được.
Quy trình một nút gửi tin nhắn như sau.
- Họ chọn ngẫu nhiên các số vô hướng L L \alpha_i \in \mathbb{F}_p α i ∈ F p , i=1,...,L i = 1 , . . . , L .
- Chúng tạo thành khối w = \sum_{i=1}^L \alpha_i w_i w = ∑ L i = 1 α i w i .
- Chúng tạo thành các số vô hướng N N a_j a j , i=1,...,N i = 1 , . . . , N theo
$$ a_j = \sum_{i=1}^L \alpha_i b_{ij}, \quad \forall j=1,…,N. $$
Thông điệp họ gửi bao gồm khối w w , các hệ số a_j a j và các cam kết C_i C i có chữ ký từ người đề xuất.
Tiêu chuẩn
Giao thức có một số thành phần chung với gossipsub, ví dụ người đề xuất cần tạo một chữ ký BLS và người xác minh phải kiểm tra một chữ ký BLS. Chúng tôi ghi lại ở đây các điểm chuẩn của các hoạt động cần thực hiện ngoài các hoạt động gossipsub thông thường. Đây là chi phí CPU mà giao thức có trên các nút. Các điểm chuẩn đã được thực hiện trên máy tính xách tay Macbook M4 Pro và trên CPU Intel i7-8550U @ 1,80GHz.
Các tham số cho các chuẩn mực này là N=10 N = 10 cho số lượng khối và tổng kích thước khối được coi là 118,75KB. Tất cả các chuẩn mực đều là luồng đơn và tất cả đều có thể song song hóa
Người đề xuất
Người đề xuất cần thực hiện các cam kết N N Pedersen. Điều này được đánh giá là
| Thời gian | Người mẫu |
|---|---|
| [25.588 ms 25.646 ms 25.715 ms] | Quả táo |
| [46,7ms 47,640ms 48,667ms] | Trí tuệ |
Các nút
Một nút nhận cần tính toán 1 cam kết Pedersen cho mỗi khối và thực hiện một tổ hợp tuyến tính tương ứng của các cam kết do người đề xuất cung cấp. Thời gian cho những điều này như sau
| Thời gian | Người mẫu |
|---|---|
| [2,6817 ms 2,6983 ms 2,7193 ms] | Quả táo |
| [4,9479 ms 5,1023 ms 5,2832 ms] | Trí tuệ |
Khi gửi một khối mới, nút cần thực hiện một sự kết hợp tuyến tính của các khối mà nó có sẵn. Thời gian cho những điều này như sau
| Thời gian | Người mẫu |
|---|---|
| [246,67 µs 247,85 µs 249,46 µs] | Quả táo |
| [616,97 µs 627,94 µs 640,59 µs] | Trí tuệ |
Khi giải mã toàn bộ khối sau khi nhận được N N khối, nút cần giải hệ phương trình tuyến tính. Thời gian như sau
| Thời gian | Người mẫu |
|---|---|
| [2,5280 ms 2,5328 ms 2,5382 ms] | Quả táo |
| [5.1208 ms 5.1421 ms 5.1705 ms] | Trí tuệ |
Tổng chi phí CPU.
Tổng chi phí chung cho bên đề xuất trên Apple M4 là 26ms luồng đơn trong khi đối với các nút nhận là 29,6ms luồng đơn. Cả hai quy trình đều có thể song song hóa hoàn toàn. Trong trường hợp của bên đề xuất, nó có thể tính toán từng cam kết song song và trong trường hợp của nút nhận, đây là các sự kiện song song tự nhiên vì nút đang nhận các khối song song từ các đối tác khác nhau. Chạy các quy trình này song song trên Apple M4 dẫn đến 2,6ms ở phía bên đề xuất và 2,7ms ở phía đối tác nhận. Đối với các ứng dụng thực tế, có thể coi các chi phí chung này là bằng không so với độ trễ mạng liên quan.
Tối ưu hóa
Một số tối ưu hóa sớm không được triển khai bao gồm việc đảo ngược hệ thống tuyến tính khi các khối xuất hiện, mặc dù bằng chứng về khái niệm được trích dẫn ở trên vẫn giữ nguyên ma trận hệ số đầu vào ở dạng Eschelon. Quan trọng nhất là các hệ số ngẫu nhiên cho các thông báo không cần phải nằm trong một trường lớn như trường Ristretto. Một trường nguyên tố nhỏ như \mathbb{F}_{257} F 257 là đủ. Tuy nhiên, vì các cam kết Pedersen diễn ra trong đường cong Ristretto, nên chúng ta buộc phải thực hiện các phép toán vô hướng trong trường lớn hơn. Việc triển khai các điểm chuẩn này chọn các hệ số nhỏ cho các tổ hợp tuyến tính và các hệ số này tăng lên ở mỗi lần nhảy. Bằng cách kiểm soát và chọn đúng các hệ số ngẫu nhiên, chúng ta có thể ràng buộc các hệ số của hệ thống tuyến tính (và do đó là chi phí băng thông khi gửi các khối) để được mã hóa bằng 4 byte thay vì 32.
Cách đơn giản nhất để thực hiện tối ưu hóa như vậy là làm việc trên một đường cong elliptic được xác định trên \mathbb{F}_q F q với q = p^r q = p r đối với một số nguyên tố nhỏ p p . Theo cách này, các hệ số có thể được chọn trên trường con \mathbb{F}_p \subset \mathbb{F}_q F p ⊂ F q .
Các cân nhắc về quyền riêng tư việc triển khai trong PoC được liên kết ở trên coi rằng mỗi nút, bao gồm cả nút đề xuất, chọn các hệ số nhỏ để kết hợp phép biến đổi tuyến tính của nó. Điều này cho phép một nút ngang hàng nhận được một khối có hệ số nhỏ để nhận ra nút đề xuất của khối. Hoặc là tối ưu hóa ở trên được sử dụng để giữ cho tất cả các hệ số nhỏ bằng cách thực hiện một thuật toán như phép mở rộng của Bareiss hoặc chúng ta nên cho phép nút đề xuất chọn các hệ số ngẫu nhiên từ trường \mathbb{F}_p F p .
Mô phỏng
Chúng tôi đã thực hiện mô phỏng quá trình lan truyền khối theo một số giả định đơn giản hóa như sau.
- Chúng tôi chọn một mạng ngẫu nhiên được mô hình hóa như một đồ thị có hướng với 10000 nút và mỗi nút có D D ngang hàng để gửi tin nhắn đến. D D được gọi là kích thước lưới trong ghi chú này và được chọn thay đổi trong phạm vi lớn từ 3 đến 80.
- Các nút ngang hàng được chọn ngẫu nhiên và thống nhất trên toàn bộ tập hợp nút.
- Mỗi kết nối được chọn với cùng băng thông X X MBps (thường được coi là X = 20 X = 20 trong Ethereum nhưng chúng ta có thể để con số này làm tham số)
- Mỗi lần nhảy mạng sẽ phát sinh độ trễ không đổi bổ sung là L L mili giây (thường được đo là L = 70 L = 70 nhưng chúng ta có thể để con số này làm tham số)
- Kích thước tin nhắn được coi là tổng kích thước B B KB.
- Đối với mô phỏng với RLNC, chúng tôi sử dụng N=10 N = 10 khối để chia khối.
- Mỗi lần một nút gửi tin nhắn đến một nút ngang hàng nhưng nút này lại hủy tin nhắn đó vì lý do trùng lặp (ví dụ: nút ngang hàng đã có khối đầy đủ), chúng tôi sẽ ghi lại kích thước của tin nhắn là băng thông bị lãng phí .
Tin đồn
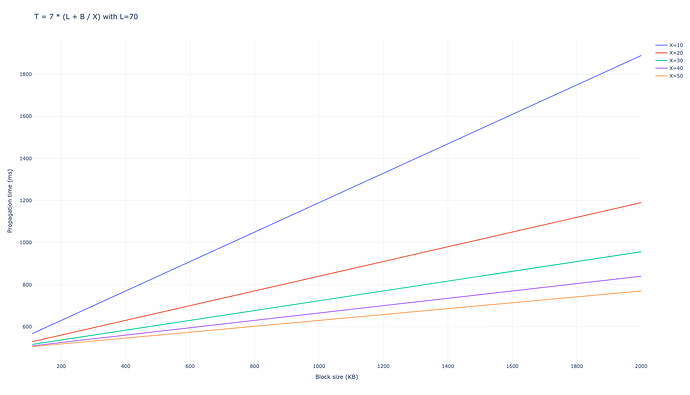
Chúng tôi đã sử dụng số lượng các đối tác để gửi tin nhắn D=6 D = 6. Chúng tôi thu được rằng mạng mất trung bình 7 lần nhảy để truyền toàn bộ khối đến 99% mạng, dẫn đến tổng thời gian truyền là
$$ T_{\mathrm{gossipsub, D=6}} = 7 \cdot (L + B/X), $$
tính bằng mili giây.
Với D=8 D = 8 kết quả tương tự
$$ T_{\mathrm{gossipsub, D=8}} = 6 \cdot (L + B/X), $$
Băng thông bị lãng phí là 94.060 \cdot B 94 , 060 ⋅ B cho D=6 D = 6 và 100.297 \cdot B 100 , 297 ⋅ B cho D=8 D = 8 .
Đối với các giá trị B B thấp, như các khối Ethereum hiện tại, độ trễ sẽ chi phối quá trình truyền bá, trong khi đối với các giá trị lớn hơn, ví dụ như truyền bá các blob sau peer-DAS, băng thông sẽ trở thành yếu tố chính.
RLNC
Một khối duy nhất cho mỗi đồng nghiệp
Với mã hóa mạng tuyến tính ngẫu nhiên, chúng ta có thể sử dụng các chiến lược khác nhau. Chúng tôi đã mô phỏng một hệ thống trong đó mỗi nút sẽ chỉ gửi một khối duy nhất cho tất cả các nút ngang hàng trong lưới có kích thước D D của chúng, theo cách này, chúng tôi đảm bảo rằng độ trễ phát sinh giống như trong gossipsub: chi phí độ trễ duy nhất là L L mili giây cho mỗi lần nhảy. Điều này yêu cầu kích thước lưới phải lớn hơn đáng kể so với N N , số lượng khối. Lưu ý rằng đối với kích thước lưới gossipsub là D_{gossipsub} D g o s s i p s u b (ví dụ: 8 8 trong Ethereum hiện tại), chúng ta sẽ cần đặt D_{RLNC} = D_{gossipsub} \cdot N D R L N C = D g o s s i p s u b ⋅ N để sử dụng cùng một băng thông cho mỗi nút, điều này sẽ là 80 80 với các giá trị hiện tại.
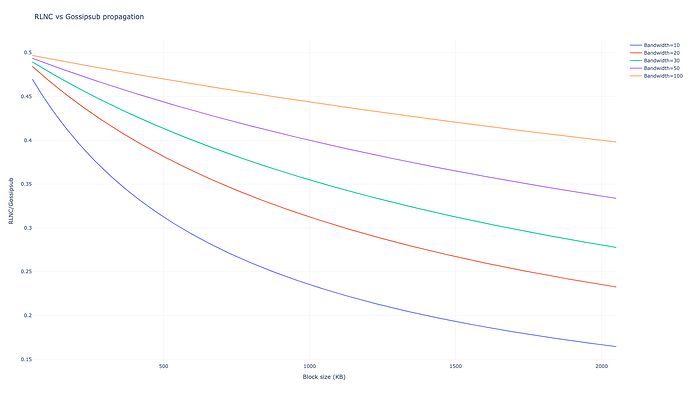
Với giá trị bảo thủ hơn nhiều là một nửa băng thông này, tức là D = 40 D = 40, chúng ta thu được
$$T_{RLNC, D=40} = 4 \cdot \left(L + \frac{B}{10 X} \right), $$
với băng thông lãng phí là 29.917\cdot B 29 , 917 ⋅ B . Giả sử cùng băng thông như ngày nay chúng ta thu được với D = 80 D = 80 chúng ta có được ấn tượng
$$T_{RLNC, D=80} = 3 \cdot \left(L + \frac{B}{10 X} \right), $$
với băng thông bị lãng phí là 28.124\cdot B 28 , 124 ⋅ B , bằng 28% băng thông bị lãng phí tương ứng trong gossipsub.
Sự khác biệt
Đối với cùng một băng thông được gửi trên mỗi nút, chúng ta thấy rằng thời gian lan truyền khác nhau cả khi chia độ trễ thành hai (có 3 hop so với 6) và khi lan truyền khối nhanh hơn, tiêu tốn một phần mười băng thông trên một đơn vị thời gian. Ngoài ra, băng thông bị lãng phí bởi các tin nhắn thừa được cắt giảm xuống còn 28% so với các tin nhắn bị lãng phí của gossipsub. Kết quả tương tự cũng thu được đối với thời gian lan truyền và băng thông bị lãng phí nhưng giảm một nửa băng thông được gửi trên mỗi nút.
Ở kích thước khối thấp hơn, độ trễ chiếm ưu thế và 3 hop so với 6 hop trên gossipsub tạo nên sự khác biệt lớn nhất, ở kích thước khối cao hơn, hiệu suất băng thông chiếm ưu thế. Đối với kích thước khối lớn hơn nhiều, chi phí CPU trong RLNC trở nên tệ hơn, nhưng xét theo thứ tự độ lớn của thời gian truyền, những điều này không đáng kể.
Nhiều khối cho mỗi đối tác
Trong phương pháp tiếp cận từng khối đơn trên mỗi đối tác trong sản xuất, các nút có băng thông cao hơn có thể chọn phát tới nhiều đối tác hơn. Ở cấp độ nút, điều này có thể được triển khai bằng cách chỉ cần phát tới tất cả các đối tác hiện tại và các nhà điều hành nút sẽ chỉ cần chọn số lượng đối tác thông qua cờ cấu hình. Một phương pháp tiếp cận khác là cho phép các nút gửi nhiều khối tới một đối tác duy nhất, theo trình tự. Kết quả của các mô phỏng này giống hệt như trên, nhưng với D D thấp hơn nhiều so với mong đợi. Ví dụ với D = 6 D = 6 , điều này sẽ không bao giờ phát một khối đầy đủ trong trường hợp một khối đơn được gửi cho mỗi đối tác. Mô phỏng mất 10 bước nhảy để phát toàn bộ khối. Với D = 10 D = 10, số bước nhảy giảm xuống còn 9.
Kết luận, thiếu sót và công việc tiếp theo
Kết quả của chúng tôi cho thấy rằng người ta mong đợi sự cải thiện đáng kể về cả thời gian truyền khối và mức sử dụng băng thông trên mỗi nút nếu chúng ta sử dụng RLNC qua giao thức định tuyến hiện tại. Những lợi ích này trở nên rõ ràng hơn khi kích thước khối/blob lớn hơn hoặc chi phí độ trễ trên mỗi bước nhảy càng ngắn. Việc triển khai giao thức này đòi hỏi những thay đổi đáng kể đối với kiến trúc hiện tại và nó có thể đòi hỏi một cơ chế pubsub hoàn toàn mới. Để biện minh cho điều này, chúng ta có thể muốn triển khai toàn bộ ngăn xếp mạng để mô phỏng theo Shadow . Một giải pháp thay thế là triển khai mã hóa và định tuyến xóa Reed-Solomon, tương tự như những gì chúng ta làm với Peer-DAS. Sẽ rất đơn giản để mở rộng các mô phỏng trên sang tình huống này, nhưng op. cit đã bao gồm nhiều so sánh như vậy.