Chúng ta luôn nghĩ rằng chúng ta có thể lật ngược thế cờ chỉ với một vòng chơi nữa, chính xác là vì chúng ta nhầm lẫn giữa số trung bình của nhóm với số phận cá nhân của mình. Hãy tưởng tượng bạn tham gia vào một trò chơi thử thách tung đồng xu như vậy với số vốn ban đầu là 1.000 nhân dân tệ và bạn có thể chọn tiếp tục chơi:
Mỗi vòng, một đồng xu sẽ được tung lên.
- Nếu bạn lật nó về mặt trước, tài sản của bạn sẽ tăng 80%.
- Nếu lật ngược lại, của cải sẽ giảm đi 50%.
Nghe có vẻ như đây là một trò chơi chắc chắn sẽ thắng!
Nhưng thực tế là…
Nếu bạn cho 100.000 người chơi tham gia trò chơi này và mỗi người chơi 100 vòng, bạn sẽ thấy rằng: tài sản trung bình của họ thực sự tăng trưởng theo cấp số nhân, nhưng tài sản cuối cùng của phần lớn họ chỉ dưới 72 nhân dân tệ, thậm chí là phá sản!
Tại sao mức tài sản trung bình tăng trưởng nhưng hầu hết mọi người lại ngày càng nghèo đi khi chơi?
Đây là một cái bẫy phi ergodic điển hình. Chúng ta luôn nghĩ rằng chúng ta có thể lật ngược tình thế chỉ với một vòng nữa, chính xác là vì chúng ta nhầm lẫn giữa số trung bình của nhóm với số phận cá nhân của mình.
Cái bẫy phi ergodic: trung bình dài hạn ≠ số phận thực sự của bạn
Tính ergodic là gì?
Khái niệm ergodicity lần đầu tiên xuất hiện trong vật lý thống kê và có tác động sâu sắc đến lý thuyết xác suất, tài chính, khoa học hành vi, học máy và các lĩnh vực khác. Câu hỏi cốt lõi mà nó cố gắng trả lời là: Liệu mức trung bình dài hạn có áp dụng được cho cá nhân không? Khi chúng ta đưa ra quyết định, chúng ta nên tin vào "mức trung bình dài hạn" hay thực tế của "trải nghiệm lần"?
Vào thế kỷ 19, nhà vật lý Ludwig Boltzmann đã đề xuất giả thuyết ergodic khi nghiên cứu chuyển động của các phân tử khí: nếu bạn quan sát một phân tử khí đủ lâu, nó sẽ trải qua mọi trạng thái có thể có.
Hãy tưởng tượng một bình chứa khí kín chứa vô số phân tử khí bên trong, mỗi phân tử trải qua một quỹ đạo vận tốc khác nhau trong quá trình va chạm. Quỹ đạo dài hạn của một phân tử riêng lẻ giống với phân phối thống kê của toàn bộ khí, điều đó có nghĩa là chúng ta có thể sử dụng trạng thái của tất cả các phân tử tại một thời điểm nhất định để suy ra quỹ đạo dài hạn của một phân tử riêng lẻ.
Đây là giả thuyết ergodic Boltzmann nổi tiếng.

Về mặt toán học, tính ergodic có nghĩa là:
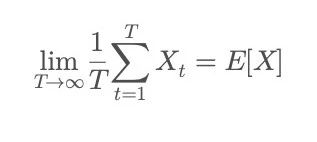
Phía bên trái là thời gian trung bình: mô tả kết quả trung bình thu được sau khi một cá nhân trải qua cùng một quá trình lần trong một khoảng thời gian đủ dài;
Phía bên phải là trung bình nhóm: mô tả kỳ vọng thống kê về kết quả quan sát vô số cá nhân tại một thời điểm nhất định. Nói cách khác, khi hệ thống đáp ứng các điều kiện ergodic, hiệu suất của một cá nhân cuối cùng sẽ hội tụ đến "trung bình dài hạn" của nhóm.
Nếu thế giới là ergodic, sự giàu có của mọi người cuối cùng sẽ hội tụ đến mức độ giàu có trung bình của xã hội. Trong một thế giới ergodic, mọi người có thể trải nghiệm tất cả các trạng thái kinh tế có thể (giàu, nghèo, thành công, thất bại), và số phận của cá nhân sẽ luôn hội tụ đến "mức trung bình dài hạn" của nhóm.
Nhưng cuộc sống thực tế thường không theo nguyên lý ergodic: các cá nhân có nguồn lực hạn chế và lần bị loại do thất bại trước khi trải nghiệm hết mọi con đường có thể.
Chúng ta thường nghe những lời nhận xét quan trọng sau:
"Thu nhập trung bình hàng năm trong một ngành công nghiệp nhất định là hơn một triệu đô la."
“Có người đã trở nên độc lập về tài chính ở tuổi 30 và bắt đầu kinh doanh riêng chỉ sau hai năm.”
"Một quỹ chỉ số nhất định có lợi nhuận hàng năm dài hạn cao. Chỉ cần bạn tiếp tục đầu tư, bạn sẽ trở nên giàu có."
…
Những số liệu thống kê có vẻ hợp lý này dường như cho chúng ta biết một sự thật nào đó. Có vẻ như miễn là chúng ta hành động, lợi nhuận trung bình dài hạn sẽ áp dụng cho các cá nhân. Nhưng những trường hợp này thuộc về sự phụ thuộc vào đường dẫn + các quá trình không ergodic không thể sao chép. Những người bắt chước không thể trải nghiệm cùng một bối cảnh lịch sử , mạng lưới quan hệ, nút may mắn hoặc thậm chí biết được số lượng những kẻ thua cuộc ẩn.
Dữ liệu cho bạn biết mức trung bình dài hạn của một nhóm, nhưng thực tế lại đầy rẫy những "thất bại thảm hại" trong ngắn hạn.
Đây là cái bẫy nguy hiểm nhất của tính phi ergodic —giá trị trung bình của số liệu thống kê dữ liệu lớn ≠ số phận thực sự của cá nhân.
Một sự sụp đổ có thể không bao giờ được bù đắp bởi một cá nhân, và một thất bại có thể loại bỏ hoàn toàn một người khỏi trò chơi, khiến không thể quay lại "trạng thái trung bình". Mỗi người chúng ta chỉ có thể trải nghiệm con đường cuộc sống một lần và chúng ta không thể lấy mức trung bình dài hạn của nhóm như một sòng bạc, chờ đợi xác suất được tính trung bình giữa lần người đánh bạc.
Tại sao số phận lâu dài của cá nhân thường tệ hơn mức "trung bình"?
Trong một hệ thống không phải ergodic, hiệu suất dài hạn của các cá nhân thường thấp hơn mức trung bình của nhóm. Đây không phải là ngẫu nhiên, mà là một đặc điểm cấu trúc có hệ thống. Mức trung bình hấp dẫn thường được đưa ra bởi những câu chuyện về một số rất ít doanh nhân thành đạt, những nhà đầu tư làm giàu nhanh chóng và phản công để vào bờ, trong khi thất bại của nhiều người khác chưa bao giờ được đưa vào số liệu thống kê.
Hệ thống thực tế có tính nhân trong hầu hết các trường hợp và có các đặc điểm phụ thuộc vào đường đi - chẳng hạn như sự kết hợp của các khoản đầu tư, suy giảm sức khỏe và tổn hại đến danh tiếng. Các đặc điểm điển hình của các hệ thống như vậy là: tăng có giới hạn và sự sụt giảm không đáy.
Phá sản có thể hủy hoại cuộc sống của bạn;
Một quyết định sai lầm lần có thể thay đổi hoàn toàn số phận của bạn;
Chỉ cần một lần vi phạm lòng tin cũng có thể phá hủy hoàn toàn lòng tin;
Tuy nhiên, sự giàu có có thể kiếm được, hiệu suất có thể tăng lên và những lợi thế có thể đạt được luôn luôn có hạn.
Đây là lý do tại sao, về mặt toán học, tăng trưởng dài hạn của một quá trình nhân không bằng “lợi nhuận trung bình”, mà gần hơn với:
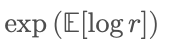
Ngược lại, điểm trung bình của nhóm thường được tính bằng cách sử dụng trung bình số học.
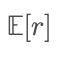
Vì hàm logarit là hàm lõm nghiêm ngặt, dựa trên bất đẳng thức Jensen, ta có:

Do đó, tăng trưởng dài hạn của hệ thống nhân (tức là trung bình nhân) luôn nhỏ hơn trung bình cộng. Biến động càng lớn, sự khác biệt này càng rõ ràng. Trung bình cộng cho bạn biết 'nếu bạn luôn may mắn thì sao', trong khi trung bình nhân cho bạn biết 'bạn còn lại bao nhiêu sau khi trải qua những thăng trầm trong thế giới thực.
Điều này có nghĩa là hiệu suất dài hạn của một cá nhân luôn thấp hơn nhiều so với "lợi nhuận trung bình của nhóm", không phải do vận rủi mà do cấu trúc.
Làm thế nào để đưa ra quyết định tốt nhất? Phần vàng của công thức Kelly
Vậy chúng ta có thể làm gì trong các quyết định cuộc sống để tránh số phận về 0 trong trò chơi dài hạn? Làm thế nào chúng ta có thể đạt được lãi kép dài hạn mà không bị phá sản?
Câu trả lời là: Đừng bao giờ cược hết tiền, hãy học cách cược cùng Kelly!
Tiêu chuẩn Kelly là một chiến lược cá cược tối ưu được sử dụng trong các trò chơi lặp lại, với mục tiêu tối đa hóa lợi nhuận dài hạn trong khi tránh thua lỗ ngắn hạn. Nó được John L. Kelly Jr. tại Bell Labs đề xuất lần đầu tiên vào năm 1956 để giải quyết vấn đề "cách phân bổ công suất tín hiệu trong kênh nhiễu" trong các hệ thống truyền thông để tối đa hóa hiệu quả truyền thông tin.
Sau đó, lý thuyết này nhanh chóng lan rộng trên nhiều lĩnh vực khác nhau.
Edward Thorp, một nhà toán học và phù thủy đầu tư người Mỹ, đã phát hiện ra rằng công thức Kelly có thể tối ưu hóa con đường tăng trưởng của cải. Ông đã mang công thức Kelly vào sòng bạc và sử dụng nó để đánh bại người chia bài blackjack một cách có hệ thống lần đầu tiên trong "Beat the Dealer". Sau đó, ông đã mang nó đến Phố Wall và tiếp tục "thu hoạch" trong "Beat the Market".
Nguyên tắc này về cơ bản tương đương với việc tối đa hóa lợi nhuận kỳ vọng logarit (log-utility), do đó tính đến sự cân bằng động giữa tăng trưởng và rủi ro. Nó giúp bạn tìm được sự cân bằng tối ưu giữa "sống lâu" và "kiếm đủ tiền".
Công thức của Kelly:
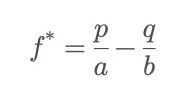
Trong đó, xác suất thành công là p, xác suất thất bại là q = 1-p; tỷ lệ lợi nhuận(không bao gồm tiền gốc) trong trường hợp thành công là b, tỷ lệ lỗ vốn trong trường hợp thất bại là a (thường là 1, nếu số tiền thua lỗ là toàn bộ số tiền đặt cược).
Quay trở lại trò chơi tung đồng xu đã đề cập ở đầu, bạn có thể chọn đặt cược một tỷ lệ phần trăm nhất định của số tiền gốc và tiếp tục chơi, nhưng số tiền cược hợp lý nhất cho lần là bao nhiêu?
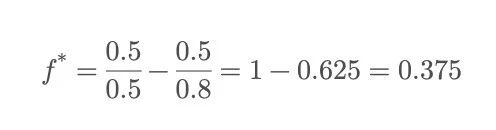
Nói cách khác, công thức Kelly khuyên bạn nên đầu tư 37,5% tổng số tiền của mình lần . Nếu bạn cược quá nhiều, ngay cả khi bạn có lợi thế, bạn có thể bị cháy tài khoản do thua lỗ lần tiếp; nếu bạn cược quá ít, bạn sẽ bỏ lỡ tăng trưởng đáng lẽ phải thuộc về bạn.
Ý nghĩa của công thức Kelly là tìm ra điểm mà bạn có thể kiếm được nhiều tiền nhất về lâu dài và vẫn có thể tồn tại.
Ngoài ra, công thức Kelly rất nhạy cảm với tỷ lệ chiến thắng, nhưng trên thực tế, các thông số này thường không chắc chắn hoặc thay đổi linh hoạt, vì vậy nhiều học viên thận trọng sẽ chọn một nửa giá trị được Kelly khuyến nghị (gọi là chiến lược nửa Kelly) để đổi lấy đường lợi nhuận mượt mà hơn.
Thí nghiệm mô phỏng: 100.000 người chơi trò tung đồng xu. Có bao nhiêu người có thể "sống sót"?
Để hiểu trực quan hơn về tác động của các chiến lược cá cược khác nhau đến vận mệnh của mỗi người, tôi đã mô phỏng 100.000 người chơi tham gia trò chơi tung đồng xu mở đầu trong tổng số 200 vòng, với mỗi người chơi chơi trò chơi một cách độc lập.
Luật chơi vẫn như vậy: tiền cược gốc là 1.000, tiền cược trước thắng 80%, tiền cược sau thua 50%. Người chơi có thể lựa chọn tỷ lệ cược cố định: ví dụ cược tất cả (100%), cược 65%, 37,5%,...
Kết quả là... 100% người chơi đặt cược đều gần như bị xóa sổ!
Cuối cùng, sự giàu có tuân theo "quy luật phân phối lũy thừa". Mặc dù một số rất ít người trở nên giàu có, nhưng phần lớn người chơi đều phá sản.
Chúng tôi đã so sánh sự phân bổ tài sản của người chơi với 4 chiến lược cá cược khác nhau này. Phân bổ tài sản càng về bên phải thì tài sản của người chơi càng cao.
a. Cược 100%: hầu như ai cũng phá sản
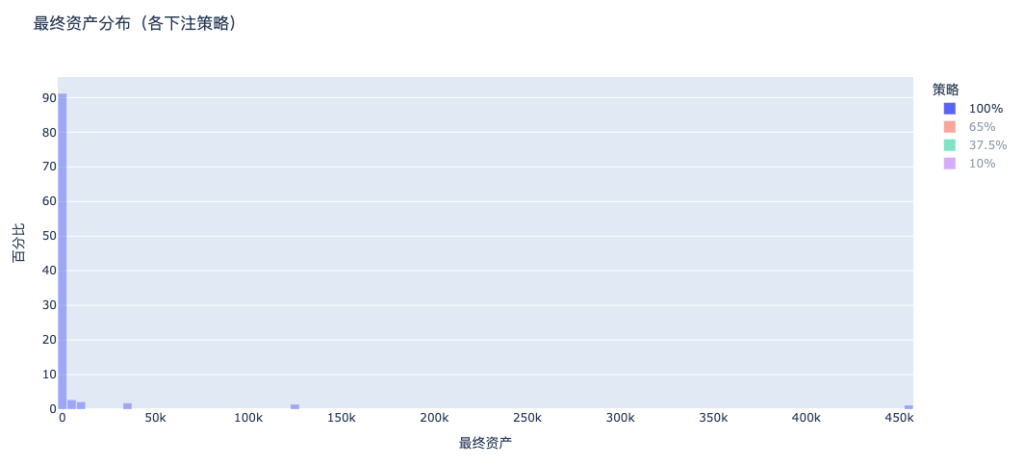
Phân phối tài sản cuối cùng theo chiến lược all-in có đỉnh nghèo đói lớn ở bên trái và đuôi giàu rất mỏng ở bên phải: hầu hết mọi người đều phá sản và rất ít người lấy hết tiền. Đây là biểu hiện thực sự của sự bất đối xứng trong trò chơi + thiên kiến sống sót.
b. Cược 65%: Vẫn phân cực, lượng lớn người dân vẫn phá sản
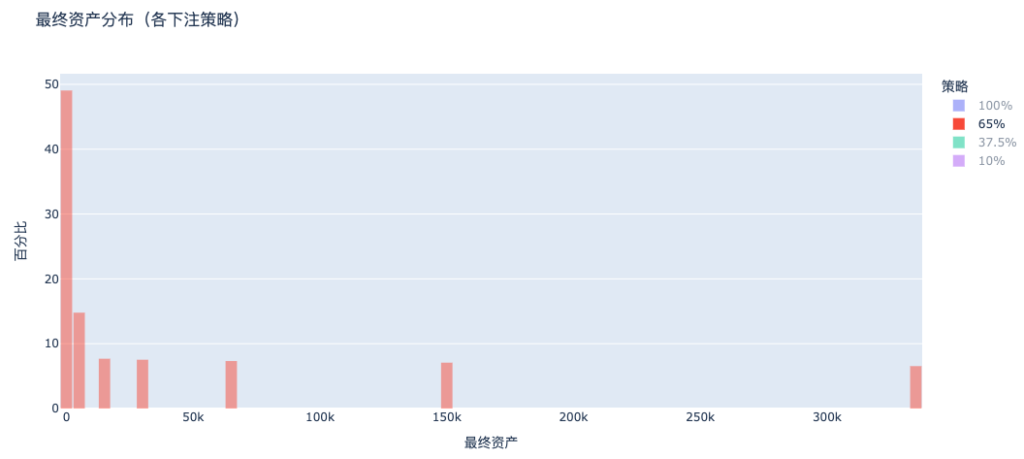
c. 37,5% cược (công thức Kelly): tăng trưởng ổn định của sự giàu có
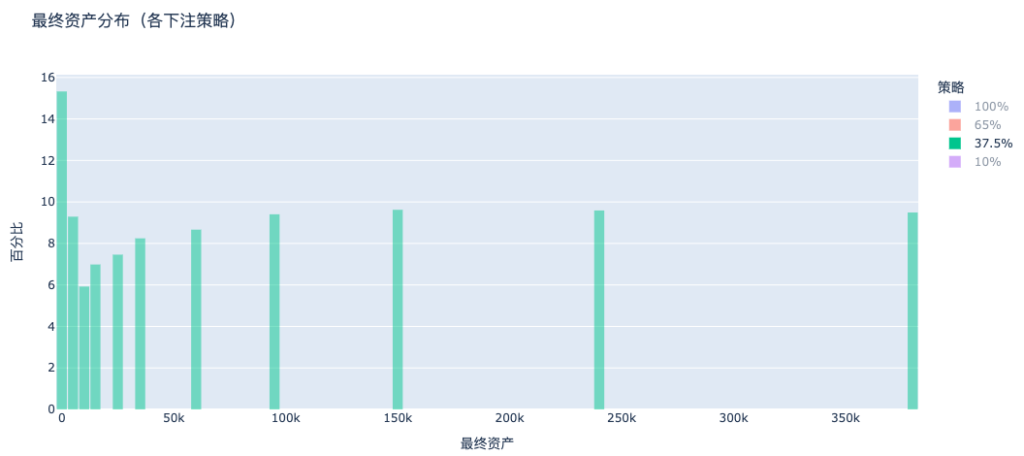
Theo chiến lược cá cược của Kelly, phân bổ tài sản đã dịch chuyển rõ ràng sang bên phải, tài sản hầu hết mọi người tăng trưởng và tập trung, đây chính là mô hình tích lũy của cải tối ưu.
d. Cược 10%: hầu như không ai phá sản nhưng lợi nhuận quá thấp
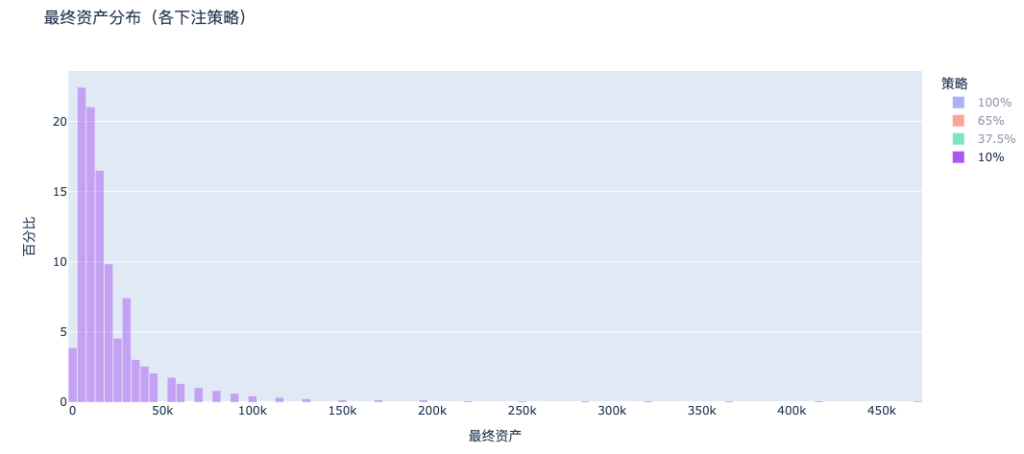
Không có đột biến phân phối phá sản như trong tình huống all-in, nhưng tổng tài sản tập trung vào khu vực tài sản thấp. Ngược lại, chiến lược 37,5% sẽ kéo ra một cái đuôi dài rõ ràng ở phía bên phải, đạt được sự nhân đôi tài sản.
Cược Kelly là chiến lược duy nhất tính đến cả "không phá sản trong hầu hết các trường hợp" và "giá trị gia tăng đáng kể", và là chiến lược sinh tồn dài hạn tối ưu về mặt toán học. Đây là bản chất của công thức Kelly: không phải là giúp bạn thắng nhiều nhất, mà là đảm bảo rằng bạn có thể sống đủ lâu.
Triết lý sống trong công thức của Kelly
Công thức của Kelly cho chúng ta biết rằng bí quyết thành công lâu dài là học cách kiểm soát tỷ lệ "đặt cược". Cuộc sống không phải là về việc ai có thể tung ra đòn chí mạng, mà là về việc ai có thể tiếp tục chơi.
Về mặt sự nghiệp, vấn đề không phải là bỏ việc vì đam mê hay bám chặt vào vùng an toàn, mà là liên tục lập kế hoạch, nâng cao khả năng, dám thay đổi nghề nghiệp và luôn giữ cho mình nhiều lựa chọn.
Trong đầu tư, không phải là dốc toàn lực để làm giàu chỉ sau một đêm, mà là kiểm soát vị thế theo tỷ lệ cược và giữ lại token;
Trong một mối quan hệ, bạn không đặt tất cả tâm lý vào một người mà hãy đầu tư trong khi vẫn duy trì bản thân mình;
Xét về mặt tăng trưởng và tính kỷ luật, sự thay đổi không đạt được thông qua một đợt bùng nổ duy nhất, mà thông qua quá trình tối ưu hóa cấu trúc cuộc sống ổn định, dựa trên lãi kép.
Cuộc sống giống như một trò chơi dài. Mục tiêu của bạn không phải là thắng một lần, mà là đảm bảo bạn tiếp tục chơi. Miễn là bạn không bỏ cuộc, những điều tốt đẹp sẽ xảy ra.







