Xin chân thành cảm ơn Alex, Csaba, Dmitry, Mikhail và Potuz đã có những cuộc thảo luận hiệu quả và đánh giá bài viết
Tóm tắt
Phương pháp DAS hiện tại cho Ethereum dựa trên mã hóa xóa Reed-Solomon + cam kết KZG. Sơ đồ mới (được mô tả tại đây Truyền Block/blob nhanh hơn trong Ethereum của @potuz ) giới thiệu một cặp khác: Mã hóa xóa RLNC (Mã hóa mạng tuyến tính ngẫu nhiên) + cam kết Pedersen. Nó có các thuộc tính tốt có thể được sử dụng để xem xét phương pháp tiếp cận Khả dụng dữ liệu thay thế.
Giao thức được nêu trong bài viết này chủ yếu phác họa thiết kế Data Availability dựa trên RLNC có thể trông như thế nào. Các khái niệm được sử dụng ở đây vẫn chưa được kiểm tra đầy đủ, chưa nói đến việc được chứng minh chính thức. Trong mọi trường hợp, nếu các khái niệm này hóa ra là đúng, thuật toán có thể đóng vai trò là nền tảng cho việc tạo nguyên mẫu. Nếu một số trong số chúng hóa ra là không chính xác, chúng ta có thể điều chỉnh thuật toán hoặc nghĩ đến việc điều chỉnh hoặc thay thế chúng.
Lý luận trong bài viết này trùng lặp ở một số điểm với bài đăng gần đây của @Csaba : Tăng tốc độ mở rộng blob với FullDASv2 (với getBlobs, mã hóa mempool và có thể là RLC) .
_Để khám phá toàn bộ bối cảnh, bao gồm lý luận và bình luận thảo luận, hãy xem phiên bản mở rộng của bài viết này: https://hackmd.io/@nashatyrev/Bku-ELAA1e_
Giới thiệu
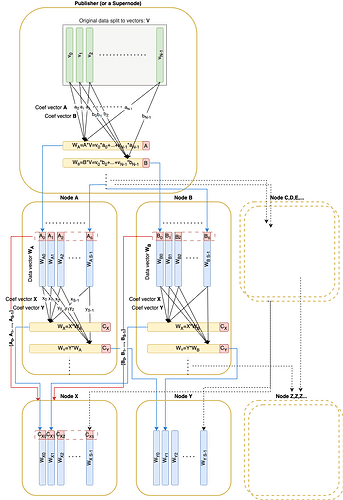
Giống như bài viết Faster Block/blob propagation trong Ethereum , dữ liệu gốc được chia thành N N vectơ v_1, \dots, v_N v 1 , … , v N trên trường \mathbb{F}_p F p . Các vectơ này có thể được mã hóa bằng RLNC và được cam kết thông qua cam kết Pedersen (kích thước 32 \times N 32 × N ) có trong Block. Bất kỳ tổ hợp tuyến tính nào cũng có thể được xác minh dựa trên cam kết và các hệ số liên quan của nó.
Chúng tôi cũng cho rằng các hệ số có thể đến từ một trường con \mathbb{C}_q C q nhỏ hơn nhiều, có kích thước có thể nhỏ bằng một byte đơn—hoặc thậm chí là một Bit đơn ( TUYÊN BỐ MIỄN TRỪ TRÁCH NHIỆM: từ các cuộc thảo luận mới nhất, vẫn chưa xác nhận được rằng chúng tôi có thể có EC an toàn trên một trường có trường con nhỏ hơn như vậy).
Chúng ta cũng hãy giới thiệu hệ số phân mảnh S S : bất kỳ nút thông thường nào cũng cần tải xuống và lưu giữ 1/S 1 / S kích thước dữ liệu gốc .
Có một hệ số Mảnh cố định S S hãy lấy tổng số vectơ ban đầu N = S^2 N = S 2
Tổng quan ngắn gọn về giao thức
Một cam kết Pedersen (kích thước 32*N 32 ∗ N ) được công bố trong Block tương ứng.
Trong quá trình phát tán, mỗi nút nhận được các vectơ kết hợp tuyến tính giả ngẫu nhiên từ các nút ngang hàng.
- thuật toán này mô tả một cách tiếp cận không tương tác trong đó các hệ số ngẫu nhiên được suy ra một cách xác định từ
nodeIdcủa người nhận và thủ thuật ma trậnRREFđược sử dụng (TUYÊN BỐ MIỄN TRỪ TRÁCH NHIỆM: thủ thuậtRREFchưa được chứng minh một cách nghiêm ngặt là hoạt động an toàn tuy nhiên có một ví dụ có thể là ý tưởng bắt đầu cho bằng chứng) - cũng có một tùy chọn dự phòng khả dụng: một cách tiếp cận tương tác trong đó người phản hồi đầu tiên tiết lộ hệ số nguồn của mình, và sau đó người yêu cầu sẽ yêu cầu kết hợp tuyến tính bằng cách sử dụng các hệ số ngẫu nhiên được tạo cục bộ.
Mỗi vectơ kết hợp tuyến tính được gửi đi đều đi kèm với các vectơ cơ sở của không gian con mà vectơ này được lấy mẫu ngẫu nhiên. Các vectơ cơ sở này phải tạo thành một ma trận ở dạng RREF. Điều kiện này đảm bảo rằng đối tác từ xa thực sự sở hữu các vectơ cơ sở cho không gian con được yêu cầu.
Nút tiếp tục lấy mẫu cho đến khi cả hai điều kiện sau được đáp ứng:
- Tất cả các vectơ cơ sở nhận được trải dài trên toàn bộ không gian N N chiều
- Ít nhất S S vector cho quyền nuôi con đã được nhận
Sau đó, nút hoàn tất việc lấy mẫu và trở thành nút 'hoạt động', có thể được các nút khác sử dụng để lấy mẫu.
Ghi chú
Các đoạn mã giống Python bên dưới chỉ nhằm mục đích minh họa, chúng không có ý định được biên dịch và thực thi ngay bây giờ. Một số hàm rõ ràng hoặc giống thư viện hiện vẫn chưa có triển khai.
Các loại
Cho các phần tử vectơ dữ liệu là từ một trường hữu hạn \mathbb{F}_p F p có thể được ánh xạ gần đúng thành 32 byte
def FScalarCho hệ số \mathbb{C}_q C q là từ một trường con của (hoặc bằng) \mathbb{F}_p F p
def CScalar Hãy để một vectơ dữ liệu duy nhất có các phần tử VECTOR_LEN từ \mathbb{F}_p F p
def DataVector = Vector[FScalar, VECTOR_LEN] Hãy để toàn bộ dữ liệu được đưa vào N DataVector gốc :
def OriginalData = Vector[DataVector, N] Derived DataVector là tổ hợp tuyến tính của các DataVector gốc . Vì vector gốc chỉ là trường hợp đặc biệt của vector phái sinh nên chúng ta sẽ không còn phân biệt giữa chúng nữa.
Để xác thực DataVector so với cam kết, cần biết hệ số kết hợp tuyến tính của nó:
def ProofVector = Vector[CScalar, N] Ngoài ra còn có một chuỗi hệ số hơi khác được sử dụng khi lấy một vectơ mới từ các DataVector hiện có:
def CombineVector = List [CScalar]Cấu trúc
Một vectơ dữ liệu đi kèm với các hệ số kết hợp tuyến tính của nó
class DataAndProof :data_vector: DataVectorproof: ProofVectorThông điệp duy nhất để truyền bá là
class DaMessage :data_vector: DataVector # coefVector for validation is derived orig_coeff_vectors: List [CombineVector]seq_no: IntCó một kho lưu trữ tạm thời cho dữ liệu Block :
class BlockDaStore :custody: List [DataAndProof]sample_matrix: List [ProofVector] # commitment is initialized first from the corresponding block commitment: Vector[RistrettoPoint]Chức năng
Hãy để hàm random_coef tạo ra một vectơ hệ số ngẫu nhiên xác định với hạt giống (nodeId, seq_no) :
def random_coef ( node_id: UInt256, length: int , seq_no: int ) -> CombineVectorHãy định nghĩa các hàm tiện ích để tính toán các tổ hợp tuyến tính:
def linear_combination ( vectors: Sequence [DataVector],coefficients: CombineVector ) -> DataVector def linear_combination ( vectors: Sequence [ProofVector],coefficients: CombineVector ) -> ProofVector Hàm thực hiện các phép toán tuyến tính trên DataVector và ProofVector đồng thời để chuyển đổi ProofVector thành RREF:
def to_rref ( data_vectors: Sequence [DataAndProof] ) -> Sequence [DataAndProof] def is_rref ( proofs: Sequence [ProofVector] ) -> boolChức năng tạo ra một thông điệp ngẫu nhiên xác định mới từ các vectơ quyền giám hộ hiện có cho một đối tác cụ thể:
def create_da_message ( da_store: BlockDaStorereceiver_node_id: uint256,seq_no: int ) -> DaMessage:rref_custody = to_rref(da_store.custody)rref_custody_data = [e.data_vector for e in rref_custody]rref_custody_proofs = [e.proof for e in rref_custody]rnd_coefs = random_coef(receiver_node_id, len (rref_custody), seq_no)data_vector = linear_combination(rref_custody_data, rnd_coefs) return DaMessage(data_vector, rref_custody_proofs, seq_no) Tính toán thứ hạng của các hệ số vectơ dữ liệu. Thứ hạng bằng N có nghĩa là dữ liệu gốc có thể được khôi phục từ các vectơ dữ liệu.
def rank ( proof_matrix: Sequence [ProofVector] ) -> intXuất bản
Nhà xuất bản nên chia dữ liệu thành các vectơ để có được OriginalData .
Trước khi truyền bá dữ liệu, nhà xuất bản phải tính toán các cam kết Pedersen (kích thước 32 * N ), xây dựng và xuất bản Block chứa các cam kết này.
Sau đó, nhà xuất bản phải điền dữ liệu vào bản lưu trữ (bản gốc) và 'bằng chứng' của chúng, đây chỉ là các thành phần của một cơ sở chuẩn: [1, 0, 0, ..., 0], [0, 1, 0, ..., 0] :
def init_da_store ( data: OriginalData, da_store: BlockDaStore ): for i,v in enumerate (data):e_proof = ProofVector([CScalar( 1 ) if index == i else CScalar( 0 ) for index in range (size)])da_store.custody += DataAndProof(v, eproof) Quá trình xuất bản về cơ bản giống như quá trình truyền bá, ngoại trừ việc nhà xuất bản gửi S tin nhắn tới một đối tác duy nhất trong một vòng duy nhất thay vì chỉ gửi 1 tin nhắn trong quá trình truyền bá.
def publish ( da_store: BlockDaStore, mesh: Sequence [Peer] ): for peer in mesh: for seq_no in range (S):peer.send(create_da_message(da_store, peer.node_id, seq_no))Nhận được
Giả sử rằng Block tương ứng được nhận và BlockDaStore.commitment được hoàn thành trước khi nhận được message: DaMessage
Lấy ProofVector từ các vector gốc:
def derive_proof_vector ( myNodeId: uint256, message: DaMessage ) -> ProofVector:lin_c = randomCoef(myNodeId, len (message.orig_coefficients),message.seq_no) return linear_combination(message.orig_coefficients, lin_c)Xác thực
Tin nhắn đầu tiên được xác thực:
def validate_message ( message: DaMessage, da_store: BlockDaStore ): # Verify the original coefficients are in Reduced Row Echelon Form assert is_rref(message.orig_coefficients) # Verify that the source vectors are linear independent assert rank(message.orig_coefficients) == len (message.orig_coefficients) # Validate Pedersen commitment proof = derive_proof_vector(my_node_id, message)validate_pedersen(message.data_vector, da_store.commitment, proof)Cửa hàng
DataVector đã nhận được sẽ được thêm vào quyền lưu giữ.
sample_matrix đang tích lũy tất cả các hệ số ban đầu và ngay khi hạng ma trận đạt N thì quá trình lấy mẫu sẽ thành công
def process_message ( message: DaMessage, da_store: BlockDaStore ) -> boolean:da_store.custody += DataAndProof(message.data_vector,derive_proof_vector(my_node_id, message))da_store.sample_matrix += message.orig_coefficientsis_sampled = N == rank(da_store.sample_matrix) return is_sampled is_sampled == true có nghĩa là chúng tôi [gần như] chắc chắn 100% rằng những người cùng gửi tin nhắn cho chúng tôi sở hữu 100% thông tin để khôi phục dữ liệu.
Truyền bá
Khi process_message() trả về True , điều này có nghĩa là việc lấy mẫu đã thành công và lưu giữ đã được lấp đầy đủ số lượng vectơ. Từ bây giờ, nút có thể bắt đầu tạo và truyền các vectơ của riêng nó.
Chúng tôi đang gửi một vectơ đến mọi đối tác trong lưới mà chưa gửi bất kỳ vectơ nào cho chúng tôi:
# mesh: here the set of peers which haven't sent any vectors yet def propagate ( da_store: BlockDaStore, mesh: Sequence [Peer] ): for peer in mesh:peer.send(create_da_message(da_store, peer.node_id, 0 ))Khả thi
Chúng ta hãy xem xét một số con số tùy thuộc vào S S và |\mathbb{C}_q| | C q | (kích thước của hệ số) giả sử kích thước dữ liệu ban đầu là 32Mb 32 M b :
| S S | sizeOf(C) (Bits) | Không có | Kích thước vectơ (Kb) | Kích thước cam kết (Kb) | Kích thước hệ số tin nhắn (Kb) | Chi phí chung của tin nhắn (%%) |
|---|---|---|---|---|---|---|
| 8 | 1 | 64 | 512 | 2 | 0,0625 | 0,01% |
| 8 | 8 | 64 | 512 | 2 | 0,5 | 0,10% |
| 8 | 256 | 64 | 512 | 2 | 16 | 3,13% |
| 16 | 1 | 256 | 128 | 8 | 0,5 | 0,39% |
| 16 | 8 | 256 | 128 | 8 | 4 | 3,13% |
| 16 | 256 | 256 | 128 | 8 | 128 | 100,00% |
| 32 | 1 | 1024 | 32 | 32 | 4 | 12,50% |
| 32 | 8 | 1024 | 32 | 32 | 32 | 100,00% |
| 32 | 256 | 1024 | 32 | 32 | 1024 | 3200,00% |
| 64 | 1 | 4096 | 8 | 128 | 32 | 400,00% |
| 64 | 8 | 4096 | 8 | 128 | 256 | 3200,00% |
| 64 | 256 | 4096 | 8 | 128 | 8192 | 102400.00% |
Theo những con số này, về cơ bản là không khả thi khi sử dụng thuật toán này với S \ge 64 S ≥ 64. Nếu không có tùy chọn nào để sử dụng hệ số nhỏ (1 hoặc 8 Bits), thì S = 8 S = 8 là hệ số phân mảnh tối đa có ý nghĩa do chi phí kích thước hệ số. (Với S = 16 S = 16 , Xuất lượng tải xuống nút tối thiểu sẽ giống như với S = 8 S = 8. )
Ưu và nhược điểm
Ưu điểm
- Tổng kích thước dữ liệu cần được phổ biến, lưu trữ và lấy mẫu là x1 (+ hệ số phụ có thể nhỏ nếu có hệ số nhỏ) của kích thước dữ liệu gốc (so với x2 đối với PeerDAS và x4 đối với FullDAS)
- Chúng ta có thể có 'hệ số Mảnh ' S S lớn tới 32 (hoặc thậm chí có thể lớn hơn với một số sửa đổi khác đối với thuật toán), điều này có nghĩa là mỗi nút chỉ cần tải xuống và lưu giữ 1/S 1 / S kích thước dữ liệu gốc. (so với 1/8 1 / 8 trong phương pháp PeerDAS hiện tại: 8 cột từ 64 gốc)
- Dữ liệu có sẵn và có thể được phục hồi bằng cách chỉ cần bất kỳ nút trung thực thông thường S S nào thực hiện lấy mẫu thành công
- Có thể thực hiện lấy mẫu bằng bất kỳ nút S S thông thường nào (so với DAS hiện tại, trong đó một nút lấy mẫu cần nhiều nút ngang hàng từ các mạng con DAS riêng biệt)
- Cách tiếp cận 'những gì bạn lấy mẫu là những gì bạn lưu giữ và phục vụ' (giống như lấy mẫu mạng con PeerDAS nhưng không giống như lấy mẫu ngang hàng phân mảnh đầy đủ). Những lo ngại liên quan đến cách tiếp cận lấy mẫu ngang hàng được mô tả ở đây
- Vì không liên quan đến việc cắt cột nên các blob riêng biệt có thể chỉ trải dài trên một số vectơ dữ liệu gốc và do đó quá trình lấy mẫu có thể được hưởng lợi hiệu quả từ nhóm giao dịch blob EL (hay còn gọi
engine_getBlobs()) - Không có mạng con nhỏ hơn nào có thể dễ bị tấn công bằng sybil
- Sự trùng lặp dữ liệu ở cấp độ vận chuyển có khả năng thấp hơn do thực tế là một nút cần các thông báo S S từ bất kỳ đối tác nào và việc sử dụng mã hóa RLNC
- RLNC + Pedersen có thể tiêu tốn ít tài nguyên hơn RS + KZG
Nhược điểm
- Kích thước cam kết và bằng chứng tăng theo cấp số nhân với hệ số phân mảnh S S .
- Nếu không có hệ số nhỏ hơn (không được chứng minh là an toàn) thì chỉ cần S = 8 S = 8 là khả thi.
- Vẫn cần ước tính độ trễ phát tán vì một nút chỉ có thể truyền dữ liệu sau khi hoàn tất quá trình lấy mẫu của riêng nó
- Đối với trường hợp hạnh phúc, số lượng đồng đẳng tối thiểu để lấy mẫu là 32 (so với 8 trong PeerDAS)
Những câu lệnh cần được chứng minh
Thuật toán trên dựa vào một số câu lệnh [nhưng chưa rõ ràng] cần phải được chứng minh cho đến nay:
- Một tổ hợp tuyến tính hợp lệ với các hệ số ngẫu nhiên được yêu cầu trả về bởi một siêu nút chứng minh rằng nút phản hồi có quyền truy cập vào toàn bộ dữ liệu (đủ vectơ để phục hồi). Tuyên bố này có vẻ không khó để chứng minh
- Nếu một nút đầy đủ tuyên bố rằng nó có các vectơ cơ sở tạo thành một không gian con hệ số, thì nếu một nút yêu cầu một vectơ ngẫu nhiên từ không gian con này và nhận được một vectơ dữ liệu hợp lệ thì nó chứng minh rằng nút phản hồi thực sự có các vectơ cơ sở cho không gian con được tuyên bố. Bằng chứng có thể là một khái quát của tuyên bố (1)
- Một EC trên \mathbb{F}_p F p với trường con \mathbb{C}_2 C 2 có ý nghĩa và an toàn. ( điều này có vẻ không đúng theo các cuộc thảo luận mới nhất )
- Thủ thuật với dạng cơ sở RREF để lấy mẫu RRT bằng không thực sự hiệu quả.
( ví dụ này có thể cung cấp một số trực giác về tính hợp lệ của tuyên bố này) - Thuật toán được mô tả tạo ra các vectơ cơ sở phân bố đều trên các nút hones cho không gian
Nchiều đầy đủ. Có mộtEkhá nhỏ (loại 1-3) sao cho hạng của các vectơ cơ sở của bất kỳ nútS + Eđược chọn ngẫu nhiên sẽ làNvới một số xác suất 'rất cao'. Điều tương tự cũng đúng trong môi trường Byzantine