Phương trình Glamsterdam

avatar
Ethereum Research
07-17
Bài viết này được dịch máy
Xem bản gốc

Phương trình Glamsterdam

Cảm ơn @potuz rất nhiều vì đã phản hồi về các mô hình. Cũng xin cảm ơn @barnabe và @terence .

Tổng quan

Phương trình Glamsterdam được thiết kế như một hướng dẫn để quyết định giữa thực thi trễ và ePBS trong bối cảnh thời gian khe ngắn hơn . Lượng gas/giây và blob thực thi tối đa được tính toán trên cả hai cấu hình đường ống khe bằng cách sử dụng một tập hợp các giả định cơ bản. Sau đó, một cấu hình khe tối đa hóa tiện ích được tính toán, dựa trên các ưu tiên của người dùng giữa khả năng mở rộng, thời gian khe, tính đơn giản và tính tin cậy. Phương trình Glamsterdam nên được xem xét như một công cụ. Nó không thể tự mình đưa ra câu trả lời chắc chắn trong cuộc tranh luận vì hai lý do:

  • Có một số quyết định mô hình hóa có thể làm sai lệch kết quả theo cả hai hướng. Một số phương pháp đơn giản hóa đã được thực hiện để tạo ra các phương trình dễ xem xét. Các hằng số được lựa chọn dựa trên phỏng đoán có căn cứ và sẽ tạo ra các kết quả khác nhau khi điều chỉnh.
  • Tất cả chúng ta đều có quan điểm khác nhau về các hằng số chủ quan hơn của phương trình tiện ích. Các đặc tính chủ quan như giá trị của một sàn giao dịch không cần tin cậy hay một thiết kế đơn giản không được định lượng, và người dùng chỉ cần cung cấp định lượng chủ quan của họ trong U_O U O. Họ cũng có thể chỉ định tầm quan trọng của các thành phần mở rộng khác nhau thông qua độ co giãn tiện ích.

Hàm tiện ích tổng thể của Glamsterdam được chỉ định là

U = (G^*_s)^{U_G} \lần (B^*_s)^{U_B} \lần (1/S^*)^{U_S} \lần U_O,
U = ( G ∗ s ) U G × ( B ∗ s ) U B × ( 1 / S ∗ ) U S × U O ,

dựa trên tỷ lệ mở rộng theo tỷ lệ trên Fusaka theo gas/s, G^*_s, G ∗ s và blobs/s, B^*_s, B ∗ s , cũng như sự giảm tương đối trong thời gian khe S^* S ∗ . Số mũ là độ co giãn tiện ích (mặc định là 1) chỉ định tầm quan trọng của các thành phần mở rộng khác nhau. Bài đăng trước tiên sẽ phân tích để suy ra tỷ lệ mở rộng có thể đạt được cho việc thực thi bị trì hoãn và ePBS tương ứng trên nhiều thời gian khe khác nhau (theo các giả định đã được đơn giản hóa), sau đó quay lại với hàm tiện ích. Sau đó, các hằng số được thay đổi để phân tích kết quả theo các giả định và tối ưu hóa khác nhau. Cuối cùng, các thiết kế thay thế được khám phá.

Hằng số

Các phương trình đường ống khe ban đầu được phân tích theo các hằng số sau, lấy đường cơ sở Fusaka giả định làm điểm khởi đầu:

Biểu tượng Giá trị Giải thích
L_G L G 0,8 giây Độ trễ toàn cầu. Thời gian cần thiết để một khối tối thiểu lan truyền đủ để hình thành sự đồng thuận.
L_D L D 0,8 giây/MB Độ trễ dữ liệu. Thời gian bổ sung cần thiết để truyền toàn bộ khối dữ liệu trên mỗi MB dữ liệu cần truyền.
L_{RF} L R F 0,2 giây Độ trễ chuyển tiếp. Độ trễ cố định khi gửi khối beacon đến chuyển tiếp.
L_{RD} L R D 0,15 giây/MB Độ trễ dữ liệu chuyển tiếp. Thời gian bổ sung cần thiết cho mỗi MB dữ liệu khi gửi khối beacon đến rơle.
b_b b b 1 MB Kích thước khối đèn hiệu. Kích thước tối đa của khối đèn hiệu phải được lắp đặt.
P_{bg} P b g 1 MB cho mỗi 60M gas Số byte tải trọng trên mỗi khí. Kích thước dữ liệu tối đa của tải trọng trên mỗi khí.
E_s E s 60M khí/giây Tốc độ thực hiện. Lượng gas tối đa có thể thực hiện được mỗi giây.
B_r B r 15 giọt/giây Tốc độ blob. Số lượng blob tối đa có thể lan truyền mỗi giây (được tính từ 48 blob/ 4-L_G 4 − L G s).
\bar{S} ¯ S 12 giây Chiều dài khe cơ sở. Chiều dài khe Fusaka cơ sở.
\bar{G}_s ¯ G s 5M khí/giây Lưu lượng khí tối đa cơ sở. Lưu lượng khí tối đa cơ sở/giây được sử dụng làm điểm tham chiếu trong hàm tiện ích (60 triệu khí/12 giây).
\bar{B}_s ¯ B s 4 đốm/giây Thông lượng blob cơ sở. Số blob cơ sở được sử dụng làm điểm tham chiếu trong hàm tiện ích (48 blob/12 giây).
A_a A a 3 giây Thời gian tổng hợp chứng thực. Thời gian cần thiết để tổng hợp chứng thực đầy đủ.
\mathrm{PTC}_d P T C d 1,4 giây Độ trễ PTC của Blob. Khoảng thời gian cần thiết ở cuối khe để phiếu bầu PTC được lan truyền.
A_d A d 0,4 giây Độ trễ của bên xây dựng. Thời gian bên xây dựng chờ sau thời hạn chứng thực trong trường hợp xấu nhất trước khi phát hành tải trọng trong ePBS.

Độ trễ rơle tổng thể được định nghĩa là L_R=L_{RF} + b_\text{b}L_{RD} L R = L R F + b b L R D , trong đó L_R L R được sử dụng trong toàn bộ bài đăng thay vì viết ra các thành phần riêng lẻ.

Hằng số là những dự đoán có căn cứ, dựa trên phân tích trước đó và các diễn biến hiện tại, ví dụ: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9. Tác động của các hằng số có độ không chắc chắn cao hơn đôi khi có thể được tính trung bình để tạo ra kết quả thực tế. Ví dụ: độ trễ dữ liệu L_D L D có thể hơi thận trọng, trong khi số byte tải trọng trên mỗi khí P_{bg} P b g lại ở mức tích cực, giả định rằng chi phí dữ liệu sẽ được điều chỉnh thêm. Để giúp người đọc hình thành quan điểm cá nhân, xin lưu ý:

  • mã nguồn để chạy phân tích và tạo biểu đồ sẽ được cung cấp trực tuyến (cuối tuần này),
  • phần kết luận khám phá những thay đổi trong cài đặt cơ sở.

Một điểm đơn giản hóa cụ thể của phân tích có thể được nhấn mạnh là tương tác giữa blob và sự lan truyền khối ở lớp ngang hàng (p2p) không được mô hình hóa, trong khi tương tác giữa khối beacon và sự lan truyền tải trọng thì có. Số lượng blob trên mỗi khe được suy ra đơn giản từ thời gian lan truyền khả dụng (phụ thuộc vào cấu trúc khe) được neo theo đặc tả Fusaka, bao gồm cùng độ trễ toàn cục L_G L G như được áp dụng cho các khối. Điều này làm cho việc phân tích dễ hiểu hơn. Tuy nhiên, vẫn còn một câu hỏi chưa có lời giải về cách thức blob tương tác với các khối, với các vai trò xác thực khác nhau và tương tác CL/EL.

Thực hiện chậm trễ

Thực thi trễ sử dụng cấu hình đơn giản, không có thời hạn tiêu đề đặc biệt và các blob phải có sẵn tại thời điểm xác nhận. Mục tiêu của phân tích là thiết lập thời hạn xác nhận A A để tối đa hóa tiện ích, phụ thuộc vào thông lượng gas và blob. Tổng lượng gas, G G , có thể được đưa vào một khe bị giới hạn bởi thời gian thực thi và thời gian truyền tải. Các ràng buộc thời gian cố định đối với việc truyền tải tải trọng có thể được biểu thị như sau:

c = L_R + L_G + b_\text{b}L_D,
c = L R + L G + b b L D ,

bao gồm độ trễ chuyển tiếp và độ trễ toàn cục cũng như sự lan truyền của khối beacon (tiêu tốn một lượng băng thông cố định không thể đồng thời được sử dụng cho tải trọng). Kích thước tải trọng tối đa cho một lượng khí G G nhất định là P_{bg}G P b g G byte, trong đó P_{bg} P b g là kích thước tải trọng tối đa trên mỗi đơn vị khí. Thời gian lan truyền tải trọng này phụ thuộc vào cửa sổ khả dụng Ac A − c , cho ràng buộc:

G \le \frac{Ac}{P_{bg} L_D}.
G ≤ A − c P b g L D .

Khí cũng bị giới hạn bởi cửa sổ thực thi, SA S − A và tốc độ thực thi, E_s E s (khí/giây), đưa ra ràng buộc thứ hai:

G \le E_s(SA).
G ≤ E s ( S − A ) .

Hạn chót tối đa hóa lưu lượng khí tiềm năng, A_G A G , được tìm thấy khi hai giới hạn trên G G bằng nhau:

E_s(S-A_G) = \frac{A_G-c}{P_{bg} L_D}.
E s ( S − A G ) = A G − c P b g L D .

Giải cho A_G A G sẽ cho kết quả:

A_G = \frac{c + E_s P_{bg} L_D S}{1 + E_s P_{bg} L_D}.
A G = c + E s P b g L D S 1 + E s P b g L D .

Tuy nhiên, mục tiêu chung là tối đa hóa tiện ích, bao gồm cả thông lượng blob. Định nghĩa tổng số blob trong một khe là B B . Các số hạng tỷ lệ của hàm tiện ích được định nghĩa là sự thay đổi của gas/giây và blob/giây tương ứng so với đường cơ sở hiện tại (được tô sáng bằng các thanh):

G_s^* = \frac{G/S}{\bar{G}_s}, \;\;\;\;\;\; B_s^* = \frac{B/S}{\bar{B}_s}.
G ∗ s = G / S ¯ G s , B ∗ s = B / S ¯ B s .

Hạn chót tối đa hóa tiện ích A_U A U được tìm thấy bằng cách tối đa hóa tích của các điều khoản tỷ lệ của hàm tiện ích tổng thể:

U_2 = (G^*_s)^{U_G} \lần (B^*_s)^{U_B}.
U 2 = ( G ∗ s ) U G × ( B ∗ s ) U B .

Một giả định hữu ích là giá trị tối ưu được tìm kiếm bị giới hạn bởi thực thi (tức là, G \propto SA G ∝ S − A ), vì thời hạn muộn hơn luôn cải thiện thông lượng blob. Để tìm giá trị tối ưu này, tiện ích logarit \ln U_2 ln U 2 được phân tích. Bỏ qua các hằng số không ảnh hưởng đến đạo hàm theo A A , hàm số được đơn giản hóa thành:

\ln U_2 = \text{const} + U_G \ln(SA) + U_B \ln(A - L_G - L_R).
trong U 2 = const + U G ln ( S − A ) + U B ln ( A − L G − L R ) .

Lấy đạo hàm theo A A ta được:

\frac{d}{dA}(\ln U_2) = -\frac{U_G}{SA} + \frac{U_B}{A-L_G-L_R}.
d d A ( trong U 2 ) = − U G S − A + U B A − L G − L R .

Đặt đạo hàm bằng 0 và giải cho A A ta được biểu thức cuối cùng:

A_U = \frac{U_B S + U_G (L_G+L_R)}{U_G + U_B}.
A U = U B S + U G ( L G + L R ) U G + U B .

Hạn chót tối ưu cuối cùng, A^* A ∗ , sau đó được chọn bằng cách chọn ứng viên sau trong hai ứng viên này, được kẹp bởi hạn chót mới nhất có thể chấp nhận được cho phép tổng hợp chứng thực, A_L = S - A_a A L = S − A a :

A^* = \min(\max(A_G, A_U), A_L).
A ∗ = min ( max ( A G , A U ) , A L ) .

Khi thời hạn cuối cùng A^* A ∗ được chọn, tổng lượng khí tuyệt đối G G có thể đạt được tại thời hạn đó có thể được tính bằng cách lấy giá trị nhỏ nhất trong hai giới hạn:

G = \min\left(E_s(SA^*), \frac{A^*-c}{P_{bg} \cdot L_D}\right).
G = phút ( E s ( S − A ∗ ) , A ∗ − c P b g ⋅ L D ) .

Từ đó, ta có thể tính được lưu lượng cuối cùng. Lượng khí mỗi giây là:

G_s = Trọng lực/S,
G s = G / S ,

và các đốm màu mỗi giây, được xác định bởi thời hạn A^* A ∗ và tốc độ lan truyền đốm màu B_r B r , là:

B_s = \frac{(A^*-L_G-L_R) \cdot B_r}{S}.
B s = ( A ∗ − L G − L R ) ⋅ B r S .

Hình 1 cho thấy thời hạn chứng thực tối ưu, có thể là:

  • cân bằng hoàn hảo giữa thời gian truyền tải trọng tải và thời gian thực hiện ( A_G A G ; màu đỏ tươi),
  • ở mức tiện ích tối ưu khi bỏ qua các ràng buộc về thời gian truyền tải trọng tải ( A_U A U ; đỏ),
  • tại thời điểm muộn nhất cho phép tổng hợp chứng thực ( A_L A L ; màu tím).

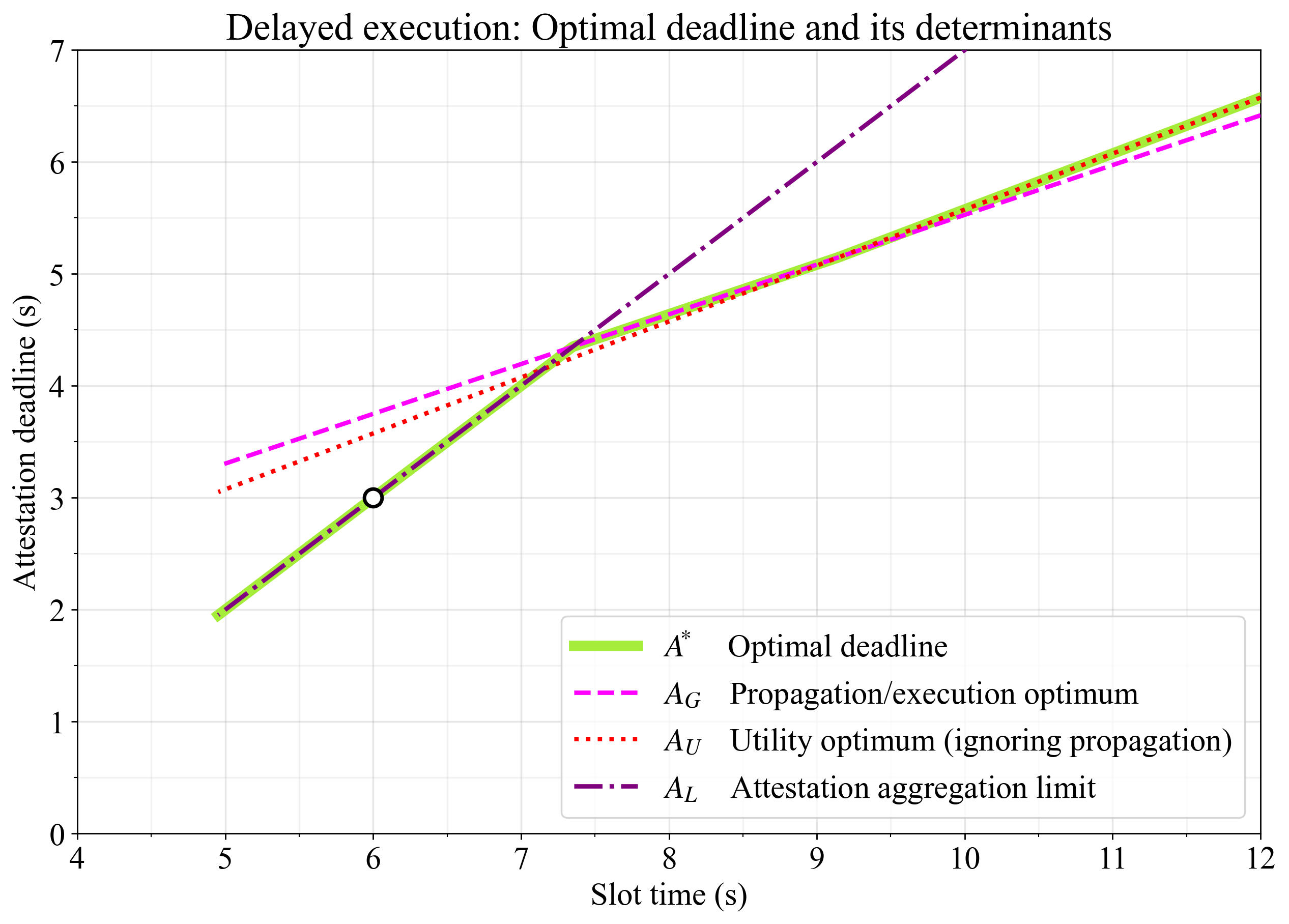
Hình 1

Hình 1. Hạn chót tối ưu trong thực thi trễ là điểm tối ưu của khí truyền/thực thi A_G A G , tiện ích cực đại trong mô hình chỉ giới hạn thực thi A_U A U , và điểm cuối cùng cho phép tổng hợp chứng thực A_L A L. Vòng tròn biểu thị mục tiêu tiềm năng tại hạn chót chứng thực là 3 giây trong khe 6 giây. Để đạt được thông lượng tối ưu, điều này sẽ yêu cầu một số tối ưu hóa để cải thiện thời gian truyền (đẩy các đường đã tối ưu xuống dưới).

Với các hằng số mặc định, thời hạn tối ưu khi khe dài 12 giây nằm ở khoảng 6,5 giây (chế độ A_U A U ). Dưới thời gian khe khoảng 9 giây, thời gian truyền tải trọng hạn chế tiện ích tối ưu cho các blob và thực thi, khiến cần phải thỏa hiệp bằng cách chọn thời hạn xác nhận muộn hơn (chế độ A_G A G ). Khi thời gian khe giảm xuống dưới khoảng 7,3 giây, không còn đủ thời gian để tổng hợp xác nhận theo A_G A G và thông lượng (truyền tải) phải được thỏa hiệp bằng cách chọn thời hạn sớm hơn (chế độ A_L A L ). Có khả năng việc triển khai thực thi bị trì hoãn theo thời gian khe 6 giây sẽ nhắm mục tiêu vào vòng tròn ở thời hạn xác nhận 3 giây (như đã được đề xuất ). Để đạt được thông lượng cao ở mức 6 giây, khi đó cần phải tăng tốc độ truyền tải (đẩy xuống các dòng được tối ưu hóa trong Hình 1) thông qua các tối ưu hóa như:

  • làm cho dữ liệu cuộc gọi đắt hơn,
  • cải thiện lớp p2p,
  • thực hiện thị trường phí đa chiều hoặc định giá vĩ mô (để giới hạn kích thước tải trọng trong trường hợp xấu nhất).

Cũng có thể giả định rằng bản thân các nhà xây dựng có thể lựa chọn các thành phần tải trọng cân bằng giữa việc truyền tải và thực thi cho bất kỳ thời hạn nào, tạo điều kiện cho việc đưa ra thời hạn sớm hơn. Tuy nhiên, điều này sẽ gây áp lực lên việc truyền tải tải trọng đối với các tải trọng có kích thước byte lớn hơn. Các tải trọng như vậy có thể không được chấp nhận ngay cả khi chúng tuân thủ giới hạn gaslimit. Đây là một trong những lý do tại sao thị trường phí đa chiều lại hấp dẫn đến vậy.

ePBS

Phương pháp thời hạn kép được sử dụng khi mô hình hóa ePBS, cho phép thời hạn PTC tải trọng tối ưu \mathrm{PTC}_P P T C P trong khi vẫn giữ thời hạn PTC DA tại thời điểm muộn nhất có thể của khe

\mathrm{PTC}_B=S-\mathrm{PTC}_d.
P T C B = S − P T C d .

Tải trọng được giải phóng trong môi trường không cần tin cậy, trong đó, trong trường hợp xấu nhất, trình xây dựng phải giải phóng tải trọng A_d A d sau thời hạn xác thực. Phụ lục A trình bày về tính liên quan của việc đưa A_d A d vào phân tích. Việc giải phóng các blob được đặt thành c c sao cho trình xây dựng không phải đợi A_d A d đếm số lượng xác thực trước khi giải phóng chúng, cho phép thời gian lan truyền lâu hơn một chút. Thời hạn xác thực trong ePBS được đặt sớm hơn trong thực thi trì hoãn, cụ thể là tại hằng số c c :

A = c = L_G + b_b L_D.
A = c = L G + b b L D .

Sau đó, tải trọng được giải phóng tại c+A_d c + A d và cũng kế thừa độ trễ toàn cục L_G L G của chính nó khi lan truyền. Nhiệm vụ duy nhất còn lại là tính toán thời hạn PTC tối ưu cho tải trọng, \mathrm{PTC}_P P T C P , được xác định nghiêm ngặt là điểm tối đa hóa tổng lượng khí, G G .

Lượng khí bị giới hạn bởi cửa sổ thực thi, S-\mathrm{PTC}_P S − P T C P và tốc độ thực thi, E_s E s (khí/giây):

G \le E_s(S-\mathrm{PTC}_P).
G ≤ E s ( S − P T C P ) .

Nó cũng bị giới hạn bởi thời gian cần thiết để truyền tải trọng tải. Một trọng tải khí G G mất tới L_G + (G \cdot P_{bg} \cdot L_D) L G + ( G ⋅ P b g ⋅ L D ) để truyền tải, và phải được phép đến nơi muộn nhất vào thời hạn \mathrm{PTC}_P P T C P :

c + A_d + L_G + (G \cdot P_{bg} \cdot L_D) \le \mathrm{PTC__P.
c + A d + L G + ( G ⋅ P b g ⋅ L D ) ≤ P T C P .

Điều này đưa ra ràng buộc về khí trong quá trình truyền:

G \le \frac{\mathrm{PTC__P - c - A_d - L_G}{P_{bg}L_D}.
G ≤ P T C P − c − A d − L G P b g L D .

Hạn chót tối ưu \mathrm{PTC}^*_P P T C ∗ P được tìm thấy khi hai giới hạn trên G G bằng nhau:

E_s(S-\mathrm{PTC__P) = \frac{\mathrm{PTC__P - c - A_d - L_G}{P_{bg}L_D}.
E s ( S − P T C P ) = P T C P − c − A d − L G P b g L D .

Giải phương trình này cho \mathrm{PTC}_P P T C P và kẹp bằng \mathrm{PTC}_B P T C B sẽ cho ra phương trình cuối cùng:

\mathrm{PTC}^*_P = \min\Bigg(\mathrm{PTC__B, \;\frac{c + A_d + L_G + E_s P_{bg} L_D S}{1 + E_s P_{bg} L_D}\Bigg).
P T C ∗ P = phút ( P T C B , c + A d + L G + E s P b g L D S 1 + E s P b g L D ) .

Khi tìm được thời hạn tối ưu \mathrm{PTC}^*_P P T C ∗ P , thông lượng cuối cùng có thể được xác định. Lượng khí mỗi giây, G_s G s , được suy ra từ ràng buộc lan truyền:

G_s = \frac{\mathrm{PTC}_P - c - A_d - L_G}{P_{bg}L_DS}.
G s = P T C P − c − A d − L G P b g L D S .

Số lượng blob trên giây, B_s B s , được xác định bởi thời gian có sẵn để lan truyền blob—từ lúc chúng được phát hành tại c c cho đến thời hạn blob \mathrm{PTC}_B P T C B , cũng tính đến độ trễ toàn cầu $L_G$ của riêng chúng—và tốc độ blob, B_r B r :

B_s = \frac{(\mathrm{PTC}_B - c - L_G) \cdot B_r}{S}.
B s = ( P T C B − c − L G ) ⋅ B r S .

Hình 2 cho thấy thời hạn tối ưu để tối đa hóa thông lượng trong ePBS theo hằng số cơ sở.

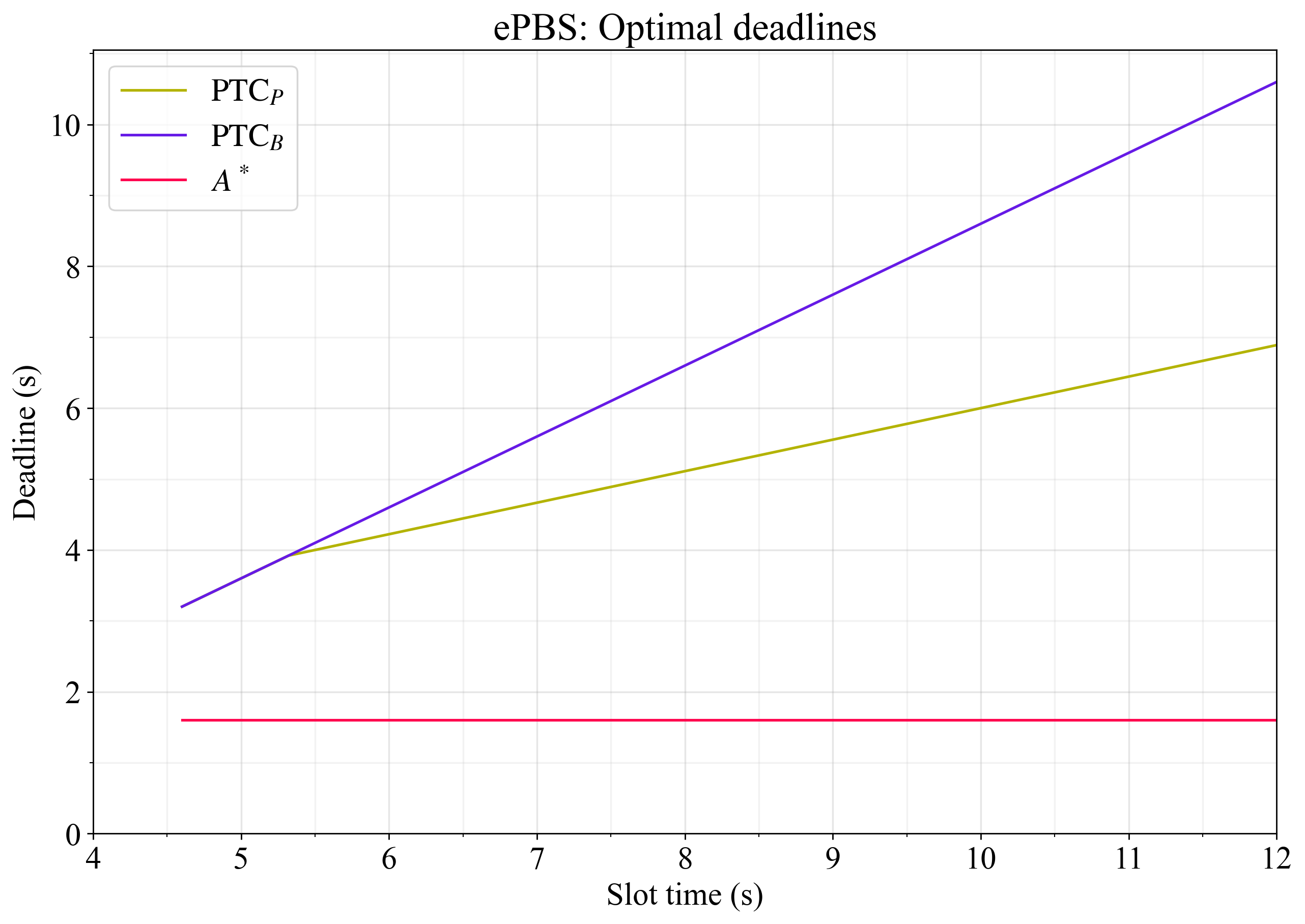
Hình 2

Hình 2. Hạn chót tối ưu để tối đa hóa thông lượng trong ePBS theo các hằng số cơ sở. Hạn chót quan sát tải trọng \mathrm{PTC}^*_P P T C ∗ P được đặt tại điểm cân bằng hoàn hảo giữa việc truyền bá và thực thi, tuân thủ giới hạn rằng nó không thể xảy ra sau khi PTC bỏ phiếu tại \mathrm{PTC}_B P T C B .

Thông lượng cho việc thực hiện chậm trễ và ePBS

Hình 3 cho thấy Mgas/giây thực thi và blob/giây đối với thực thi trễ và ePBS. Như đã thấy, ePBS đặc biệt phù hợp để mở rộng blob, nhờ hạn chót PTC muộn mà nó cung cấp. Vì hạn chót trên tải trọng có thể được thiết lập độc lập, nên thông lượng giảm dần đều khi thời gian khe rút ngắn cho đến khi quá trình truyền cuối cùng bị giới hạn dưới 5,5 giây. Thông lượng giảm dần đều do tầm quan trọng tương đối ngày càng tăng của:

  • sự chậm trễ toàn cầu L_G L G ,
  • thời gian lan truyền khối đèn hiệu c c ,
  • thời gian mà người xây dựng yêu cầu để xác định rằng khối đèn hiệu sẽ thu thập đủ chứng thực A_d A d ,
  • và thời gian lan truyền phiếu bầu PTC \mathrm{PTC}_d P T C d .

Thực thi trễ là tốt nhất để mở rộng quy mô khí L1 ở thời gian khe dài hơn , vì có ít độ trễ hơn khi bắt đầu khe, và thời hạn xác nhận có thể được cân bằng hợp lý giữa việc truyền và thực thi với các hằng số mặc định. Sau đó, đường cong thông lượng bị cong khi ràng buộc tổng hợp xác nhận bắt đầu có hiệu lực vào khoảng 7,3 giây. Thông lượng giảm đáng kể so với độ dài khe này, do không đủ thời gian để truyền theo các hằng số cơ sở.

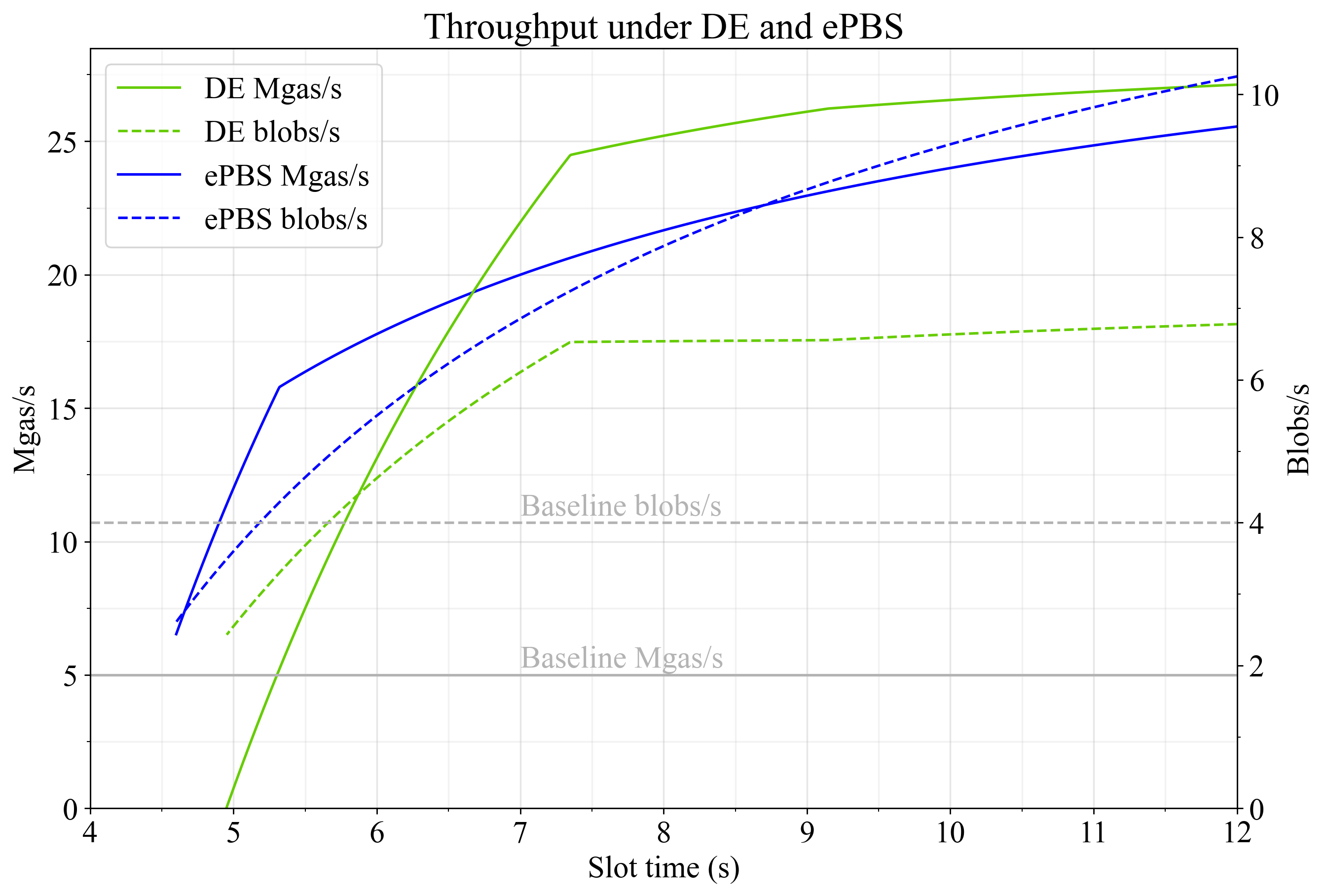
Hình 3

Hình 3. Thông lượng khi thực hiện trễ (màu xanh lá cây) và ePBS (màu xanh lam) tại các thời điểm khác nhau, được chỉ định là Mgas/giây (đường đầy đủ) và blob/giây (đường nét đứt). Cả hai phương pháp đều có tiềm năng mở rộng Ethereum đáng kể, ngay cả khi thời gian thực hiện ngắn hơn.

Tiện ích theo phương trình Glamsterdam

Phương trình Glamsterdam nắm bắt được quy mô từ việc tái cấu trúc khe, tính đến sự thay đổi tương đối trong thời gian khe S^* S ∗ và một hệ số quy mô chủ quan U_O U O để nắm bắt bất kỳ cân nhắc bổ sung nào. Ai đó có thể gán U_O>1 U O > 1 cho DE nếu tính đơn giản của việc không thay đổi lựa chọn nhánh và không có PTC được ưu tiên. Mặt khác, nếu việc thanh toán không cần tin cậy giữa người xây dựng và người đề xuất được coi là quan trọng, ai đó có thể thay vào đó gán U_O>1 U O > 1 cho ePBS. Phương trình đầy đủ là:

U = (G^*_s)^{U_G} \lần (B^*_s)^{U_B} \lần (1/S^*)^{U_S} \lần U_O.
U = ( G ∗ s ) U G × ( B ∗ s ) U B × ( 1 / S ∗ )

Nguồn
Tuyên bố từ chối trách nhiệm: Nội dung trên chỉ là ý kiến của tác giả, không đại diện cho bất kỳ lập trường nào của Followin, không nhằm mục đích và sẽ không được hiểu hay hiểu là lời khuyên đầu tư từ Followin.
Thích
Thêm vào Yêu thích
Bình luận
Nội dung liên quan