Tôi muốn cảm ơn @aelowsson vì đã đánh giá và phản hồi.
Mục tiêu của phân tích này là để hiểu trạng thái Ethereum (kích thước cơ sở dữ liệu trên mỗi nút đầy đủ) có thể phát triển như thế nào khi giới hạn gas khối tăng lên và cách định giá lại (thay đổi chi phí gas hiệu quả cho byte trạng thái và tài nguyên bùng nổ) ảnh hưởng đến cả sự phát triển của trạng thái và thông lượng bùng nổ như thế nào.
Để đạt được điều này, chúng tôi:
- Quy mô dự án theo ba quỹ đạo giới hạn khí (cơ sở, tích cực, bảo thủ).
- Xây dựng và hiệu chỉnh mô hình nhu cầu đẳng đàn hồi đơn giản để tạo trạng thái và tiêu thụ tài nguyên đột biến.
- Sử dụng mô hình đó để tính toán phí cơ sở cân bằng EIP-1559 mới và chia sẻ tài nguyên theo khối khi giới hạn gas và/hoặc giá gas để thêm trạng thái thay đổi.
- Báo cáo so sánh các kịch bản trên nhiều phạm vi độ co giãn giá cho nhu cầu đột biến và nhu cầu của tiểu bang.
Tóm tắt
- Tiểu bang có thể tăng trưởng đáng kể nếu thông lượng tăng trong khi chi phí tạo tiểu bang vẫn tương đối rẻ. Đến giữa năm 2027, quy hoạch bảo thủ sẽ đạt tổng quy mô tiểu bang là 686 GiB, quy hoạch cơ bản là 859 GiB, và quy hoạch tích cực là 1,08 TiB. Trong mọi trường hợp, con số này đều vượt ngưỡng quan trọng 650 GiB được xác định bởi sáng kiến bloatnet .
- Chúng ta cần thống nhất về mức tăng trưởng nhà nước có thể chấp nhận được đối với Ethereum trong trung và dài hạn.
- Việc tăng chi phí khí đốt để tạo trạng thái sẽ làm giảm mức tăng trưởng trạng thái dự kiến trên các chế độ đàn hồi đã khám phá, nhưng lại làm giảm nhẹ thông lượng tài nguyên bùng nổ.
- Tổn thất thông lượng chịu ảnh hưởng nhiều hơn bởi độ co giãn của nhu cầu bùng nổ so với chi phí tạo trạng thái. Khi nhu cầu bùng nổ co giãn theo giá, việc tăng gấp đôi công suất vẫn mang lại mức tăng thông lượng gần như tuyến tính và việc định giá lại chỉ có tác động nhỏ.
- Nếu nhu cầu tạo lập trạng thái không co giãn, việc tăng chi phí tạo lập trạng thái dự kiến sẽ dẫn đến mức phí cơ sở cao hơn so với kịch bản trạng thái không được định giá lại. Nếu nhu cầu này co giãn, hiệu ứng này sẽ đảo ngược.
1. Tại sao chúng ta quan tâm đến sự phát triển của nhà nước?
Tính đến tháng 5 năm 2025, kích thước cơ sở dữ liệu chưa nén hiện tại trong một nút Geth dành riêng cho trạng thái là ~340 GiB. Sau khi tăng giới hạn gas từ 30M lên 36M đơn vị gas, kích thước trung bình của các trạng thái mới được tạo ra mỗi ngày đã tăng gấp đôi, từ ~102 MiB lên ~205 MiB.
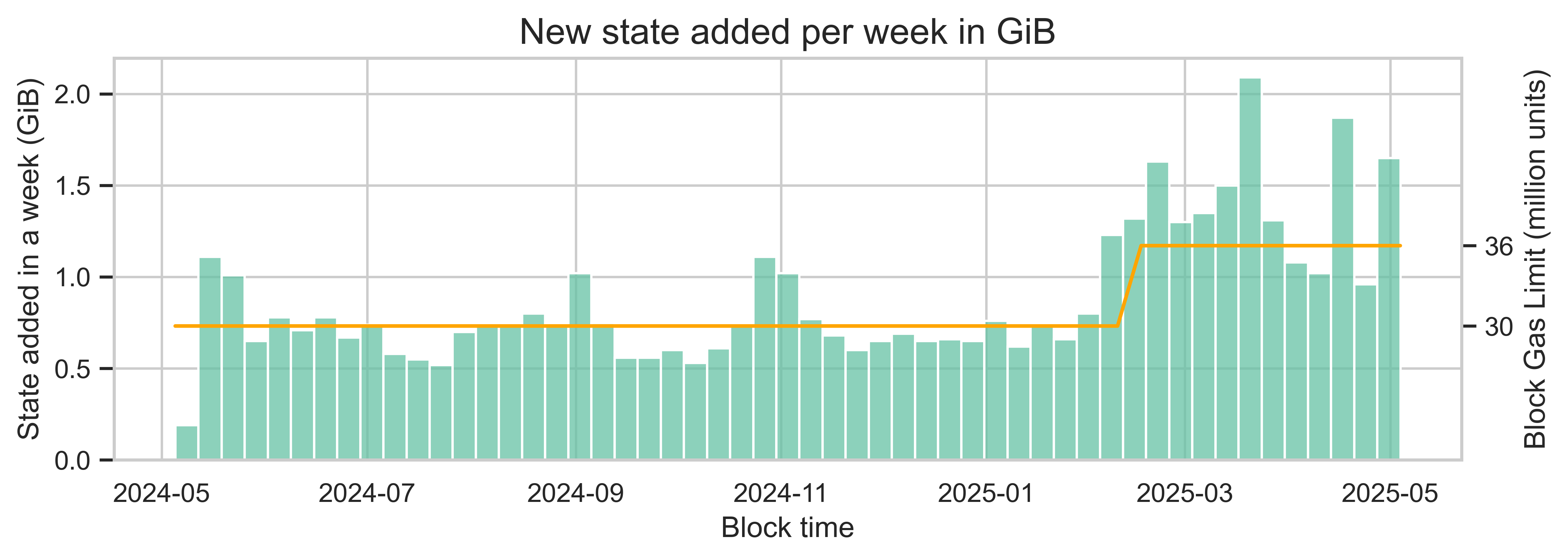
Mối quan hệ chúng ta thấy trong ví dụ này không tuyến tính như mong đợi. Điều này có thể do các yếu tố khác tác động đến hành vi người dùng. Tuy nhiên, nếu mọi thứ đều như nhau, chúng tôi kỳ vọng số lượng trạng thái mới được tạo ra sẽ tăng theo tỷ lệ thuận khi giới hạn gas tăng.
Tốc độ tăng trưởng cao của tiểu bang có hai tác động tiêu cực ở hạ lưu:
- Nếu trạng thái tăng nhanh hơn mức cải thiện của đĩa và sự giảm dung lượng lưu trữ trên mỗi byte, cuối cùng chúng ta sẽ đạt đến điểm mà trình xác thực bị đẩy giá lên cao và không thể đáp ứng được các yêu cầu về đĩa cần thiết để chạy một nút xác thực Ethereum.
- Hiệu suất của các hoạt động truy cập trạng thái như
SSTOREphụ thuộc đáng kể vào kích thước của trạng thái, với trạng thái lớn hơn dẫn đến thời gian thực thi chậm hơn. Sáng kiến bloatnet đã xác định được các điểm nghẽn nghiêm trọng trong các mẫu truy cập trạng thái với kích thước trạng thái là 650 GiB, dẫn đến thời gian truy cập trạng thái tăng 40%, mức tiêu thụ bộ nhớ tăng theo cấp số nhân và thời gian đồng bộ hóa lâu hơn.
Vẫn chưa rõ việc cải tiến phần cứng và tối ưu hóa máy khách sẽ ảnh hưởng đến những điểm nghẽn này như thế nào; tuy nhiên, xét đến việc hiện tại đang tập trung vào khả năng mở rộng và dự kiến sẽ tăng giới hạn gas, đây là vấn đề chúng ta cần xem xét kỹ lưỡng hơn. Trên hết, chúng ta cần thống nhất về mức tăng trưởng trạng thái chấp nhận được cho Ethereum trong trung và dài hạn.
Tuy nhiên, trong báo cáo này, chúng tôi tập trung vào một câu hỏi hơi khác: giới hạn khí đốt dự kiến sẽ ảnh hưởng đến tăng trưởng của tiểu bang như thế nào và việc điều chỉnh giá khí đốt có thể thay đổi quỹ đạo tăng trưởng ra sao. Điều này đặc biệt liên quan đến EIP-8037 , dự án được đề xuất cho nhánh Glamsterdam sắp tới.
2. Kịch bản tăng trưởng của nhà nước theo giới hạn khối ngày càng tăng: nhà nước có thể phát triển đến mức nào?
Để trả lời câu hỏi này, chúng tôi đã thiết kế ba lịch trình khác nhau để tăng giới hạn khí đốt từ ngày 01/05/2025 đến giữa năm 2027:
| Ngày | Thận trọng | Căn cứ | Hung dữ |
|---|---|---|---|
| 2025-05-01 | 36 | 36 | 36 |
| 2025-07-01 | 45 | 45 | 45 |
| 2025-12-01 | 60 | 60 | 60 |
| 2026-06-01 | 80 | 100 | 150 |
| 2026-12-01 | 150 | 300 | 500 |
| 2027-06-01 | 200 | 400 | 700 |
Sau đó, đối với mỗi lịch trình, chúng tôi tính toán tốc độ tăng trưởng trạng thái tương ứng, giả sử có mối quan hệ tỷ lệ giữa tốc độ tăng trưởng trạng thái mỗi ngày và giới hạn khí và tốc độ tạo trạng thái cơ sở được đo là 205 MiB/ngày ở giới hạn khí 36M:
new_state_per_day = 205 MiB * (G / 36M)
Với điều này, chúng ta có được tốc độ tăng trưởng trạng thái sau đây mỗi ngày tại mỗi ngày thay đổi giới hạn khí:
| Ngày | Bảo thủ (MiB/ngày) | Cơ sở (MiB/ngày) | Mạnh mẽ (MiB/ngày) |
|---|---|---|---|
| 2025-05-01 | 205 | 205 | 205 |
| 2025-07-01 | 256 | 256 | 256 |
| 2025-12-01 | 342 | 342 | 342 |
| 2026-06-01 | 456 | 569 | 854 |
| 2026-12-01 | 854 | 1708 | 2847 |
| 2027-06-01 | 1139 | 2278 | 3986 |
Biểu đồ tiếp theo cho thấy tổng quy mô của tiểu bang tính theo GiB trong 2 năm tới đối với ba lịch trình khí đốt.
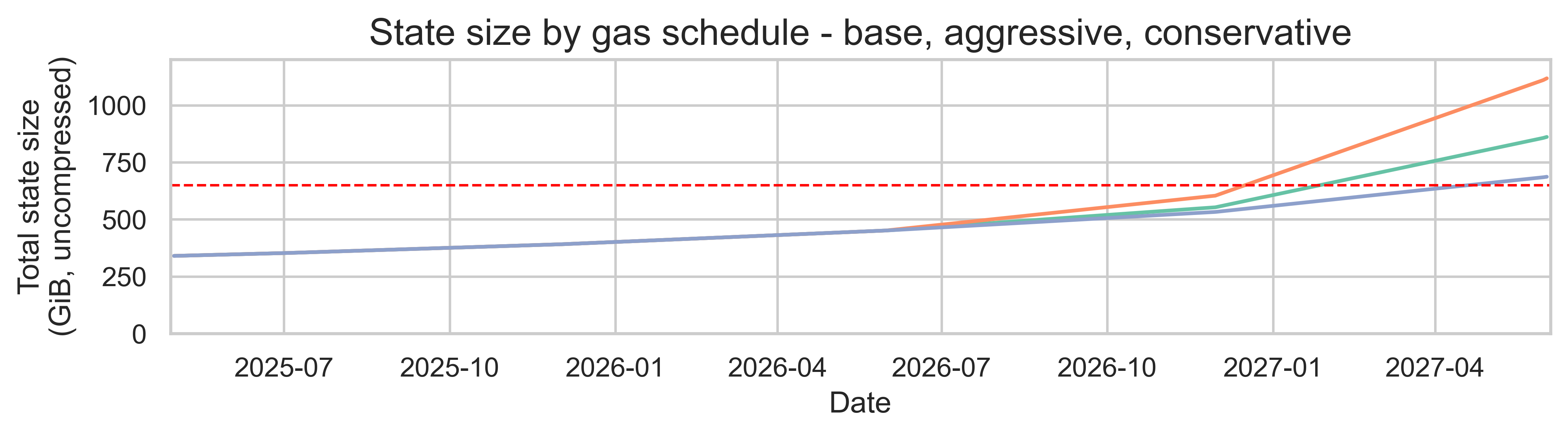
Theo phương pháp mở rộng theo tỷ lệ (giữ nguyên thành phần khí), việc tăng giới hạn khối sẽ làm tăng tuyến tính lượng trạng thái được tạo ra hàng ngày (vì chúng tôi chia tỷ lệ 205 MiB/ngày đo được theo tỷ lệ giới hạn khí). Do lượng bổ sung hàng ngày được gộp lại, tổng kích thước trạng thái sẽ khác nhau theo tháng và năm giữa các lịch trình khí. Đến giữa năm 2027, lịch trình bảo thủ đạt tổng kích thước trạng thái là 686 GiB, lịch trình cơ sở là 859 GiB, và lịch trình tích cực là 1,08 TiB. Trong mọi trường hợp, con số này đều vượt quá ngưỡng quan trọng 650 GiB được xác định bởi sáng kiến bloatnet .
3. Việc định giá lại tác động như thế nào đến sự tăng trưởng và thông lượng của tiểu bang?
Bây giờ chúng ta đã xác định được các kịch bản tiềm năng về tăng trưởng trạng thái mà không có thay đổi về giá, chúng ta có thể phân tích cách tăng giá gas cho các hoạt động tạo lập trạng thái ảnh hưởng đến tăng trưởng và khả năng mở rộng của trạng thái như thế nào.
3.1 Mô hình và suy luận
Chúng tôi bắt đầu bằng cách xác định một mô hình đơn giản cho phép ước tính mức tăng trưởng trạng thái trung bình hàng ngày và lượng khí có sẵn trong một khối cho các hoạt động bùng nổ (tính toán, truy cập trạng thái và dữ liệu).
Đầu vào mô hình
- G G : Giới hạn khí khối.
- b b : Phí cơ sở cân bằng b b trong gwei.
- g_\text{state} g state : Chi phí gas cho mỗi byte mới được thêm vào byte trạng thái.
- g_\text{burst} g burst : Chi phí gas cho mỗi giây sử dụng tài nguyên burst.
- S(p) S ( p ) : Đường cong nhu cầu tạo trạng thái, được đo bằng tổng số byte trạng thái ròng sẵn sàng được thêm vào một khối với mức giá p p . Lưu ý rằng p p là chi phí tính bằng gwei khi thêm một byte vào trạng thái và được tính như sau: p=b\cdot g_\text{state} p = b ⋅ g state .
- B(p) B ( p ) : Đường cong nhu cầu bùng nổ tài nguyên, được đo bằng số thời gian khe (giây) sẵn sàng được thêm vào một khối ở mức giá p p . Trong trường hợp này, p=b\cdot g_\text{burst} p = b ⋅ g burst .
Giả định mô hình
- Phí cơ bản tuân theo thiết kế EIP-1559, trong đó việc sử dụng khối trên 50% G G sẽ dẫn đến việc tăng phí cơ bản cho khối tiếp theo, trong khi việc sử dụng khối dưới 50% G G sẽ dẫn đến việc giảm phí cơ bản cho khối tiếp theo.
- Với thiết kế hiện tại, các khối chiếm trung bình 50% G G , trong đó 30% lượng khí được phân bổ để tạo trạng thái và phần còn lại để khai thác tài nguyên.
- Khối trung bình đạt được ở trạng thái cân bằng khi 50% G G đủ để đáp ứng nhu cầu tạo trạng thái và sử dụng tài nguyên bùng nổ ở mức giá p p .
- Cả hai đường cầu đều được mô hình hóa bằng hai mô hình đẳng đàn hồi độc lập:
Ở đây, chúng tôi giả định các nhu cầu đẳng đàn hồi độc lập về khả năng xử lý. Tuy nhiên, trên thực tế, nhu cầu tạo trạng thái và tài nguyên burst có thể có mối tương quan: sự thay đổi giá hiệu dụng của byte trạng thái sẽ ảnh hưởng đến nhu cầu giây burst (và ngược lại). Một đặc tả nhu cầu đa biến kết hợp với độ co giãn giá chéo sẽ nắm bắt tốt hơn sự thay thế hoặc bổ sung giữa các tài nguyên, nhưng nó lại đưa ra các tham số bổ sung và thách thức về nhận dạng.
Kịch bản
- Giới hạn khí tăng theo hệ số n n , tức là G = n \, G^0 G = n G0
- Chi phí khí đốt của tiểu bang tăng theo hệ số m m , tức là, g_\text{state} = m \, g_\text{state}^0 g state = m trạng thái g 0
Chúng tôi kỳ vọng mức phí cơ bản sẽ giảm cho đến khi đạt được trạng thái cân bằng mới, trong đó cả trạng thái và tài nguyên bùng nổ đều được sử dụng.
Đạo hàm cơ sở
Giả sử mức sử dụng cân bằng cho mỗi khối ở mức giá p p là
- Các byte trạng thái: S(p)=S(b g_\text{state}) S ( p ) = S ( b g state )
- Giây bùng nổ: B(p)=B(b g_\text{bùng nổ}) B ( p ) = B ( b g bùng nổ )
Lượng khí được sử dụng trong một khối ở mức phí cơ sở b được định nghĩa như sau:
Đối với kịch bản này, EIP-1559 điều khiển b b hướng tới giá trị b^* b ∗ sao cho:
Ở trạng thái cân bằng mới này, chúng ta có được mức sử dụng theo từng khối như sau:
- S^* = S(b^* \, m\, g_\text{trạng thái}^0) S ∗ = S ( b ∗ tôi g 0 state ) , dẫn đến mức tăng trưởng trạng thái trung bình là 2.628.000\cdot S^* 2 , 628 , 000 ⋅ S ∗ byte mỗi năm. Lưu ý rằng 2.628.000 2 , 628 , 000 là số khối mỗi năm (tức là một khối sau mỗi 12 giây)
- B^* = B(b^* g_\text{burst}^0) B ∗ = B ( b ∗ g 0 burst )
và các chia sẻ sau đây cho mỗi loại tài nguyên:
- \text{Chia sẻ}_\text{trạng thái}=\frac{m\,g_\text{trạng thái}^0S^*}{0.5\, n\, G_\text{giới hạn}^0} Trạng thái chia sẻ = m g 0 trạng thái S ∗ 0,5 N Giới hạn G 0
- \text{Chia sẻ}_\text{burst}=1-\text{Chia sẻ}_\text{state} Chia sẻ burst = 1 − Chia sẻ trạng thái
Sự định cỡ
Với G=G^0 G = G 0 hiện tại, cân bằng b=b^0 b = b 0 và giá khí ban đầu g_\text{state}^0 g 0 state và g_\text{burst}^0 g 0 burst , ta có:
- g_\text{trạng thái}^0 S(b^0 g_\text{trạng thái}^0)= 0,3 \cdot 0,5 \cdot G^0 = 0,15\, G^0 g 0 trạng thái S ( b 0 g 0 trạng thái ) = 0,3 ⋅ 0,5 ⋅ G 0 = 0,15 G0
- g_\text{burst}^0 B(b^0 g_\text{burst}^0)= 0,7 \cdot 0,5 \cdot G^0 = 0,35\, G^0 g 0 burst B ( b 0 g 0 burst ) = 0,7 ⋅ 0,5 ⋅ G 0 = 0,35 G0
Với điều này, chúng ta có thể hiệu chỉnh A_s A s và A_b A b như sau:
A_s = S(p)p^{\varepsilon_s} = \frac{0,15\,G^0}{g_\text{state}^0}\,(b^0g_\text{state}^0)^{\varepsilon_s} A s = S ( p ) p ε s = 0,15 trạng thái G 0 g 0 ( b 0 g 0 trạng thái ) ε s
A_b = B(p)p^{\varepsilon_b} = \frac{0.35\,G^0}{g_\text{burst}^0}\,(b^0g_\text{burst}^0)^{\varepsilon_b} A b = B ( p ) p ε b = 0,35 G 0 g 0 nổ ( b 0 g 0 bùng nổ ) ε b
Theo lựa chọn này, với bất kỳ b b nào, ta có công thức sau cho khí được sử dụng trong khối ở trạng thái cân bằng:
Chúng ta cũng có thể ước tính g_\text{burst}^0 g 0 burst từ giới hạn khí và tốc độ tăng trưởng trạng thái hiện tại. Ở đây, chúng ta lấy chi phí trung bình với giả định mức sử dụng giới hạn khí là 50%:
Đối với các tài nguyên bùng nổ, chúng ta sẽ định giá dựa trên khối trường hợp xấu nhất, nghĩa là, giả sử rằng nếu khối chứa đầy các hoạt động tài nguyên bùng nổ cho đến khi đạt đến giới hạn khối, thì sẽ mất 2 giây để thực hiện:
Từ đó, chúng ta có thể trực tiếp suy ra thông lượng cơ sở cho các tài nguyên bùng nổ:
Suy ra kịch bản
Trong trường hợp này, G=n\,G^0 G = n G 0 , g_\text{state}=m\,g_\text{state}^0 g state = m trạng thái g 0 và g_\text{burst}=g_\text{burst}^0 g burst = g 0 burst , khiến tổng lượng khí được sử dụng trong khối ở trạng thái cân bằng là:
Ngoài ra, ở trạng thái cân bằng, chúng ta đang sử dụng 50% giới hạn khí mới nên:
Ta có thể tính các nghiệm của đa thức này để tìm cơ sở cân bằng b^* b ∗ . Nếu đa thức có nghiệm r \in \mathopen] 0,1\mathclose[ r ∈ ] 0 , 1 [ , thì b^* = b^0 \, r b ∗ = b 0 r . Từ đó, chúng ta có thể tính toán mức sử dụng theo khối và chia sẻ khí như được định nghĩa trong phép suy luận cơ sở.
Trong các phần sau, chúng tôi xem xét tác động của ba kịch bản:
- Cơ sở (không định giá lại): n=2 n = 2 (giới hạn gas gấp đôi), m=1 m = 1 (chi phí gas không đổi)
- Giá xăng hai tiểu bang: n=2, m=2 n = 2 , m = 2
- Giá xăng ba tiểu bang: n=2, m=3 n = 2 , m = 3
Trong mọi trường hợp, chúng tôi giả định rằng giới hạn khí tăng gấp đôi ( n=2 n = 2 ).
Đối với mỗi kịch bản, chúng tôi quét \varepsilon_s ε s và \varepsilon_b ε b trên một lưới (0,1 đến 1,5) và giải tìm b^* b ∗ . Với phí cơ sở cân bằng b^* b ∗ , sau đó chúng tôi tính S^* S ∗ , B^* B ∗ , mức tăng trưởng hàng năm của trạng thái GiB và tỷ lệ khí tài nguyên. Để dễ hình dung hơn, đồ thị sau đây cho thấy trạng thái cân bằng mới này cho kịch bản cơ sở với giả định \varepsilon_s=0,6 ε s = 0,6 và \varepsilon_b=1 ε b = 1
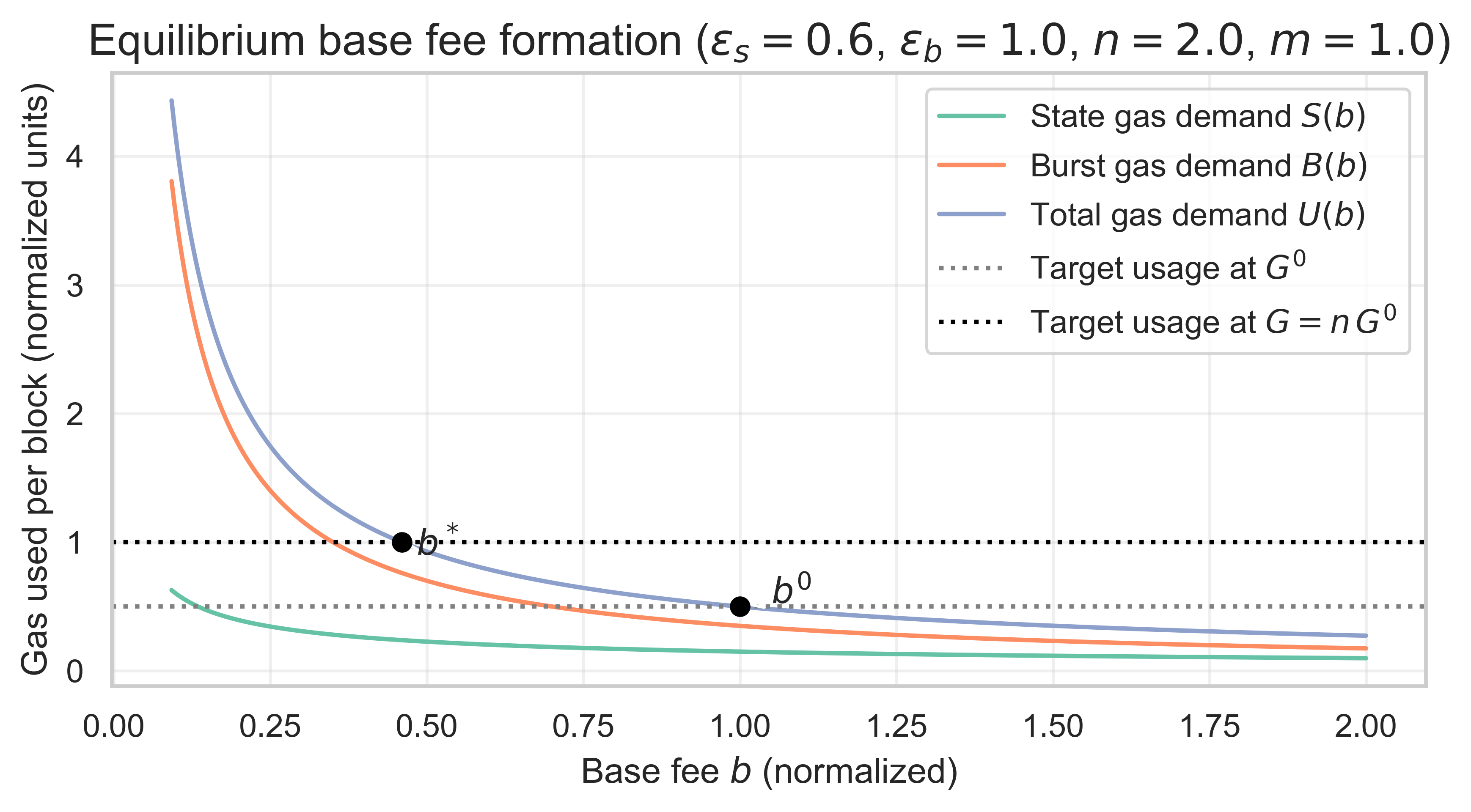
3.2 Tác động của việc định giá lại đến tỷ trọng khí đốt được sử dụng bởi các cơ sở nhà nước
Các biểu đồ sau đây cho thấy tỷ lệ khí được sử dụng trong khối cân bằng theo các hoạt động tạo trạng thái cho tất cả các kết hợp độ co giãn giá (\varepsilon_s, \varepsilon_b) ( ε s , ε b ) .
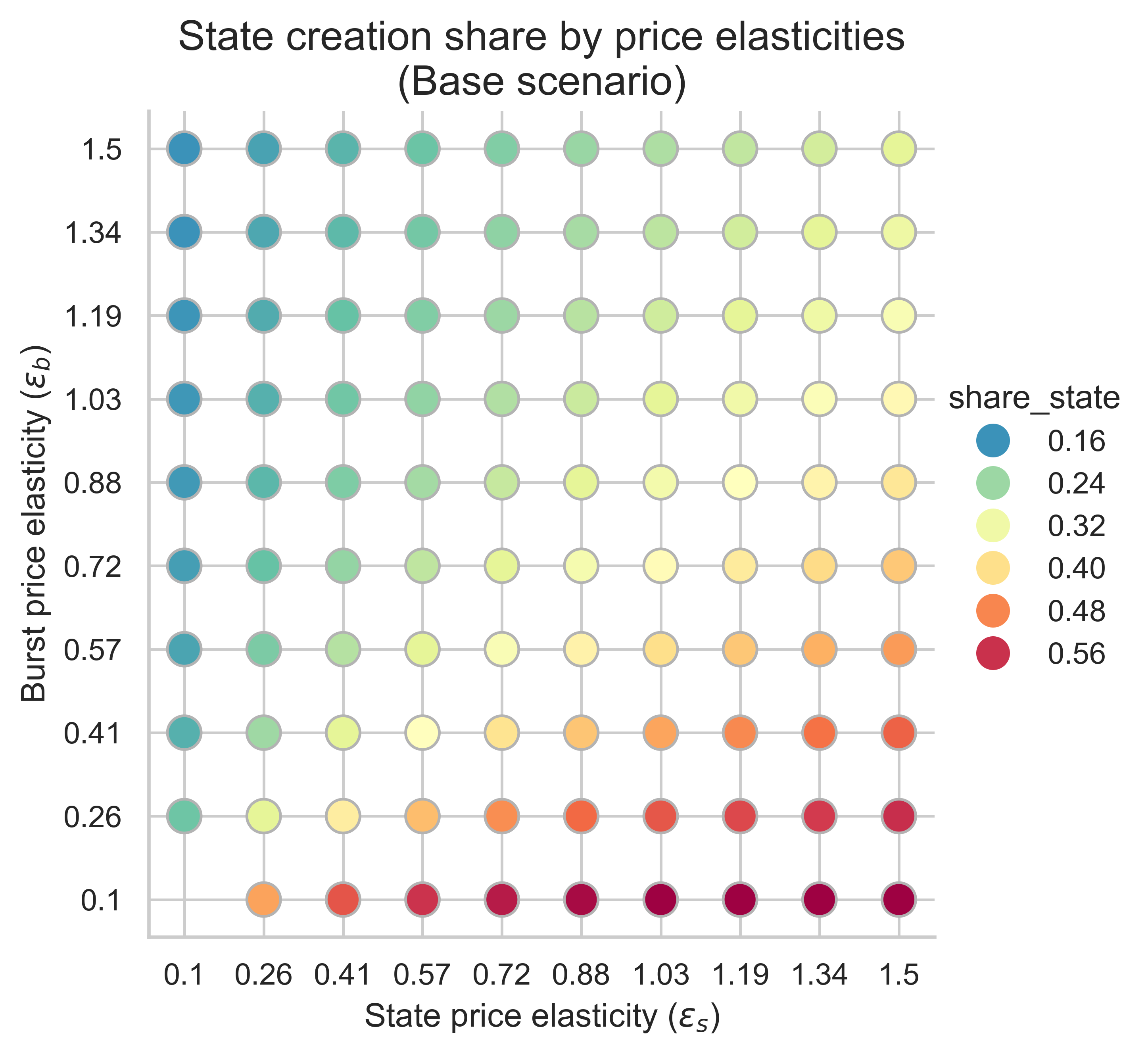
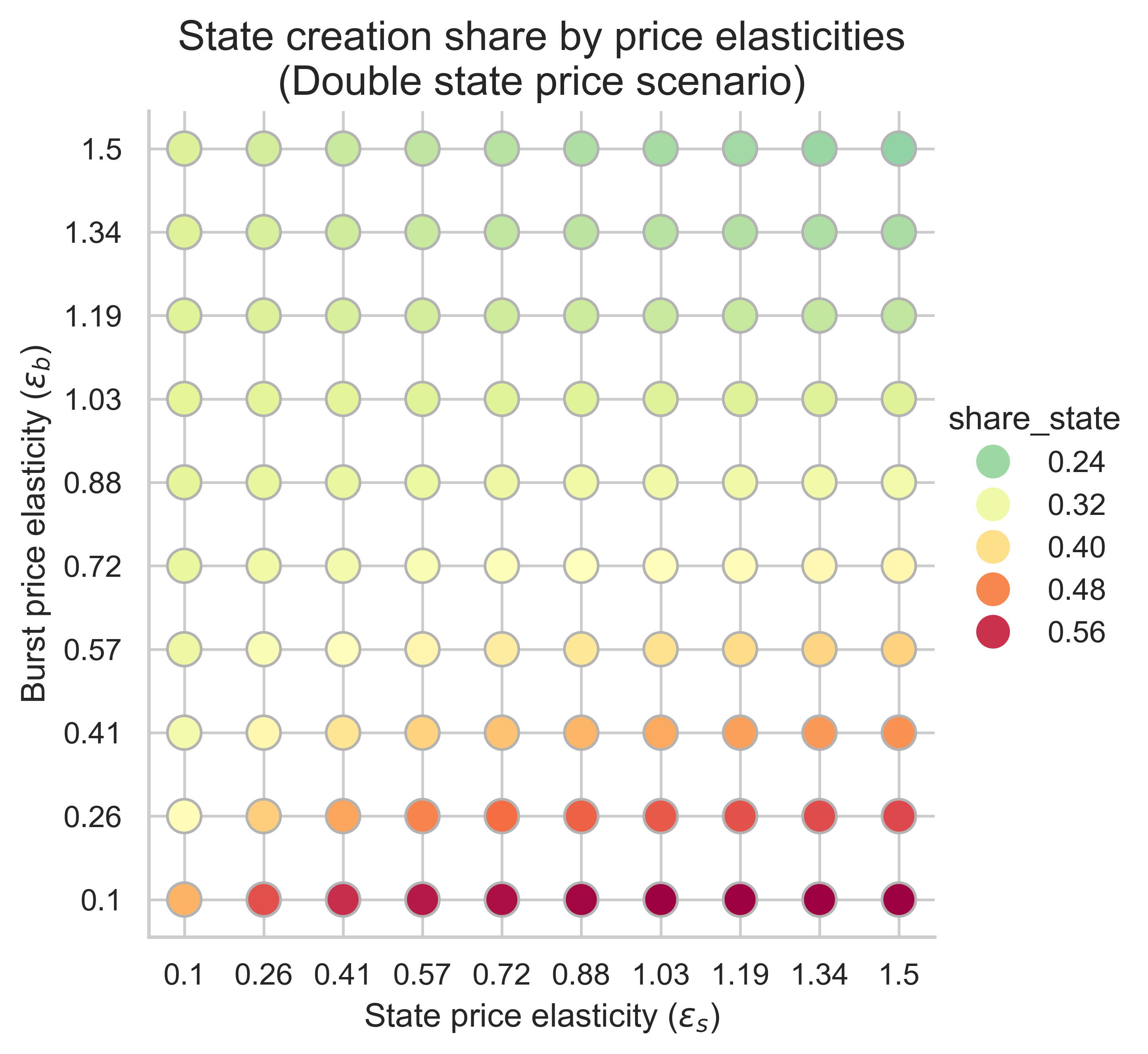
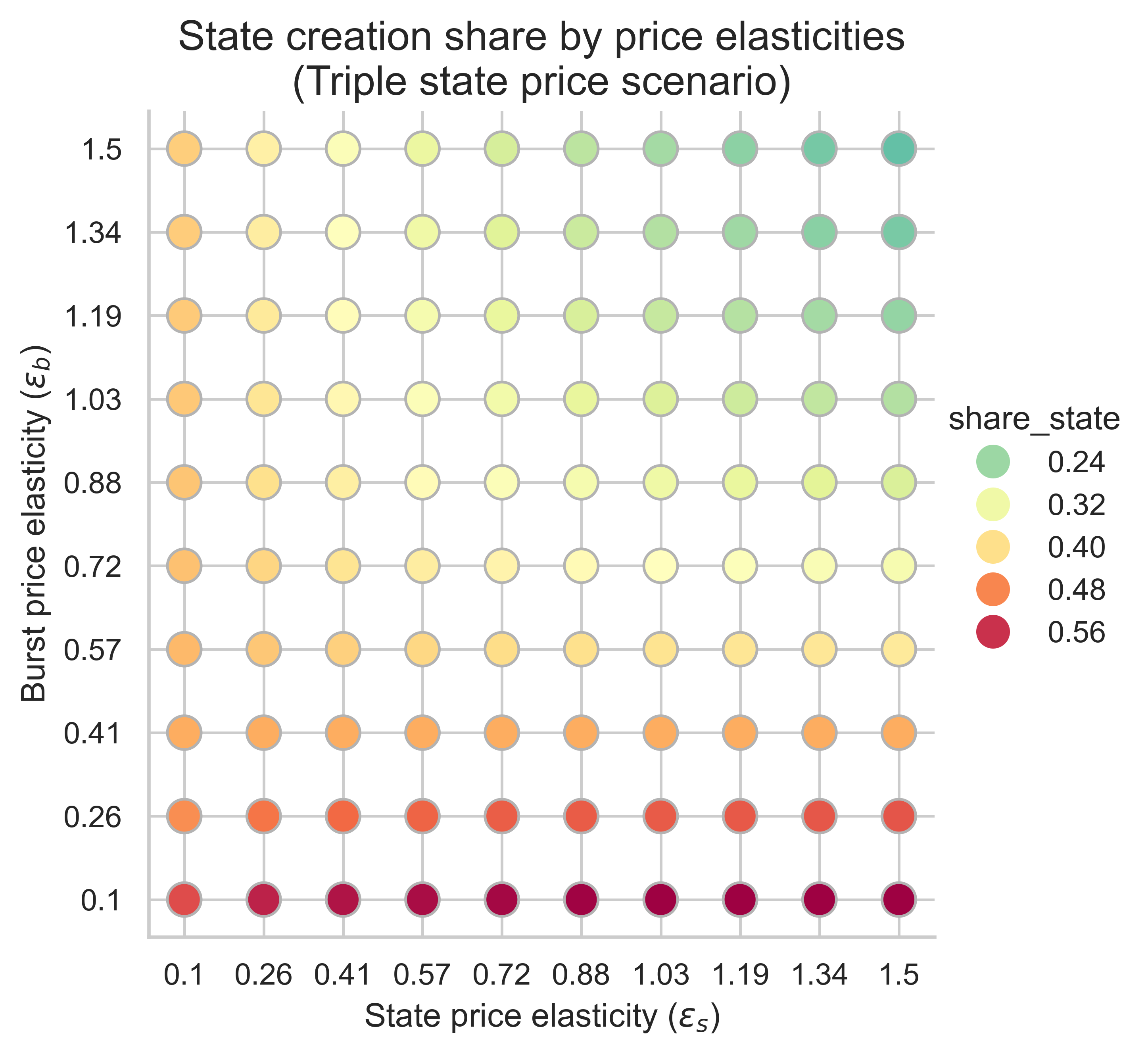
Với m = 1 m = 1 (không định giá lại) và n = 2 n = 2 (giới hạn gas gấp đôi), tỷ lệ gas khối được sử dụng để tạo trạng thái tăng lên so với mức 30% hiện tại khi nhu cầu tạo trạng thái co giãn hơn nhu cầu tài nguyên burst. Do đó, nếu việc tạo trạng thái thích ứng nhiều hơn với sự thay đổi giá hơn là việc sử dụng tài nguyên burst, thì việc tăng giới hạn gas sẽ có nguy cơ chuyển nhiều dung lượng khối sang việc tạo trạng thái hơn, vì nhu cầu tạo trạng thái lớn hơn sẽ làm tràn ngập khối để tận dụng mức phí cơ sở rẻ hơn.
Việc tăng m m (khiến việc tạo trạng thái trở nên tốn kém hơn) sẽ tác động đến phần chia sẻ khối dành cho việc tạo trạng thái trong chế độ trạng thái có độ đàn hồi thấp và chế độ có độ đàn hồi cao của tài nguyên bùng nổ:
- Khi nhu cầu tạo trạng thái có độ co giãn thấp (phía bên trái của biểu đồ), chúng ta thấy tỷ lệ khí dành cho hoạt động tạo trạng thái cao hơn, m m càng lớn thì độ lớn càng tăng.
- Ngược lại, khi cả hai nhu cầu đều có độ đàn hồi cao (góc trên bên phải), hiệu ứng sẽ đảo ngược, với phần khối dành cho việc tạo trạng thái giảm dần khi so sánh với kịch bản m = 1 m = 1. Độ lớn của sự thay đổi lại phụ thuộc vào m m .
- Các trường hợp có tỷ lệ tạo trạng thái cao nhất xảy ra khi nhu cầu về tài nguyên bùng nổ có độ đàn hồi thấp (phía dưới của biểu đồ). Trong trường hợp này, việc tăng chi phí tạo trạng thái không có tác dụng.
Tóm lại, việc tăng chi phí khí tạo trạng thái có thể có tác động tích cực hoặc tiêu cực đến tỷ lệ khối cân bằng dành cho việc tạo trạng thái. Điều này phụ thuộc vào chế độ đàn hồi. Tuy nhiên, khi tỷ lệ không gian khối dành cho việc tạo trạng thái đã cao trong kịch bản cơ sở ( m = 1 m = 1 ), thì việc tăng chi phí khí tạo trạng thái không ảnh hưởng đáng kể đến tỷ lệ này. Nói cách khác, nếu chúng ta đang ở trong một chế độ đàn hồi đã có tỷ lệ khí tạo trạng thái cao khi giới hạn khối tăng dần, thì việc tăng giá khí sẽ không có tác động đáng kể.
3.3 Tác động của việc định giá lại đối với tăng trưởng hàng năm của tiểu bang
Các biểu đồ sau đây cho thấy mức tăng trưởng trạng thái hàng năm cho tất cả các kết hợp độ co giãn giá (\varepsilon_s, \varepsilon_b) ( ε s , ε b ) . Ở đây, chúng tôi giả định rằng khối trung bình là khối cân bằng. Chỉ số này là chìa khóa để hiểu mức độ hiệu quả của việc tăng chi phí hoạt động tạo trạng thái trong việc giảm thiểu sự phát triển của trạng thái.
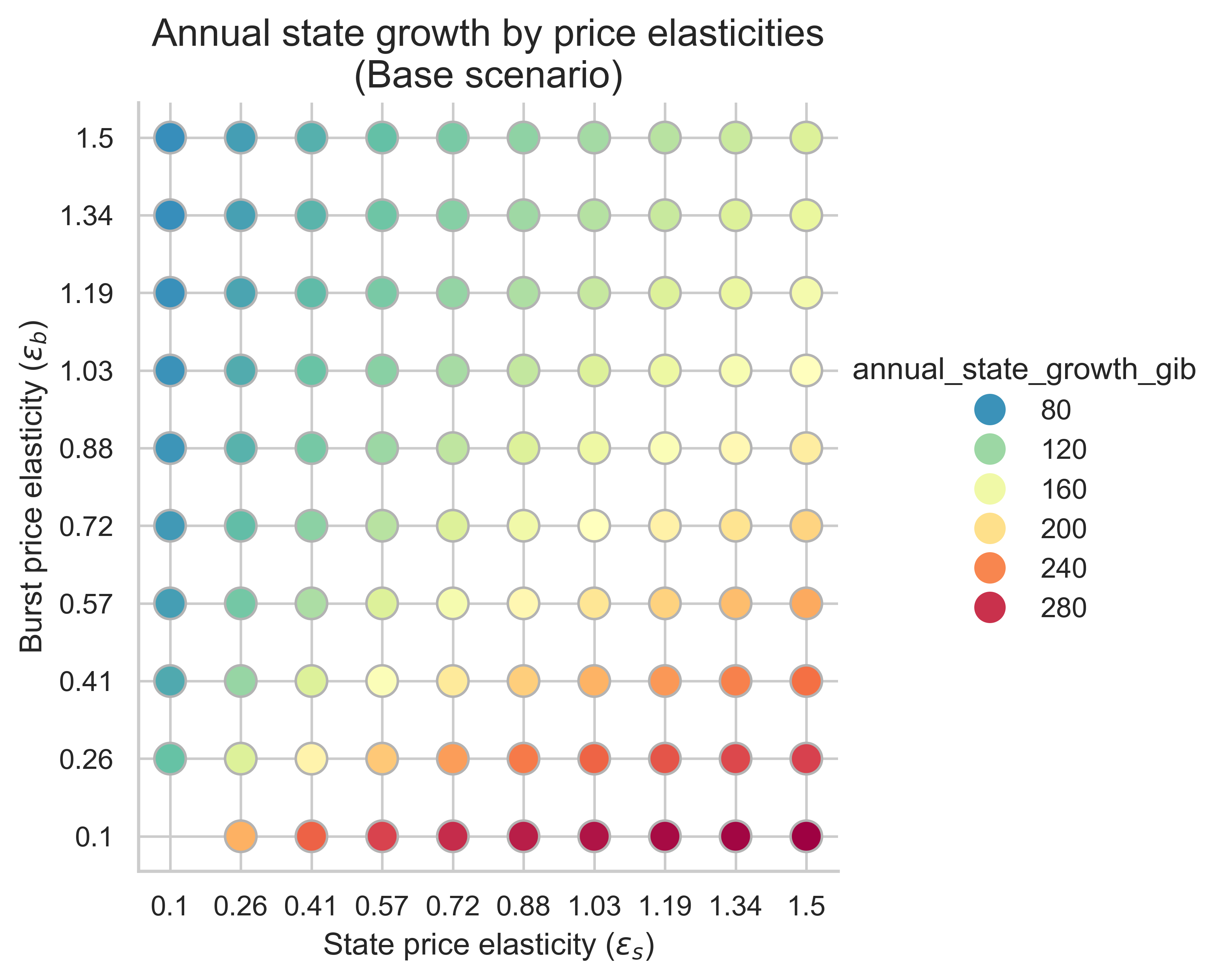
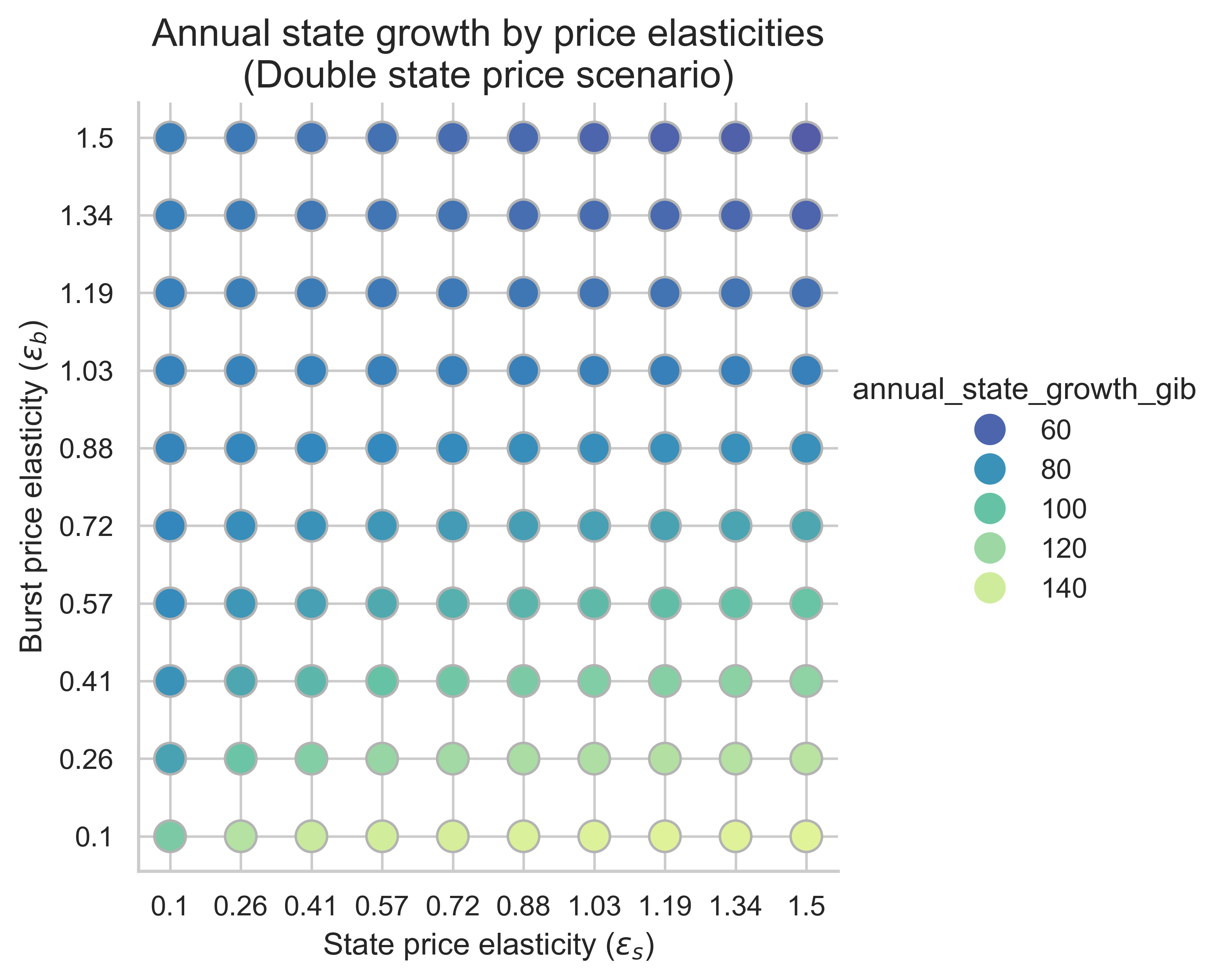
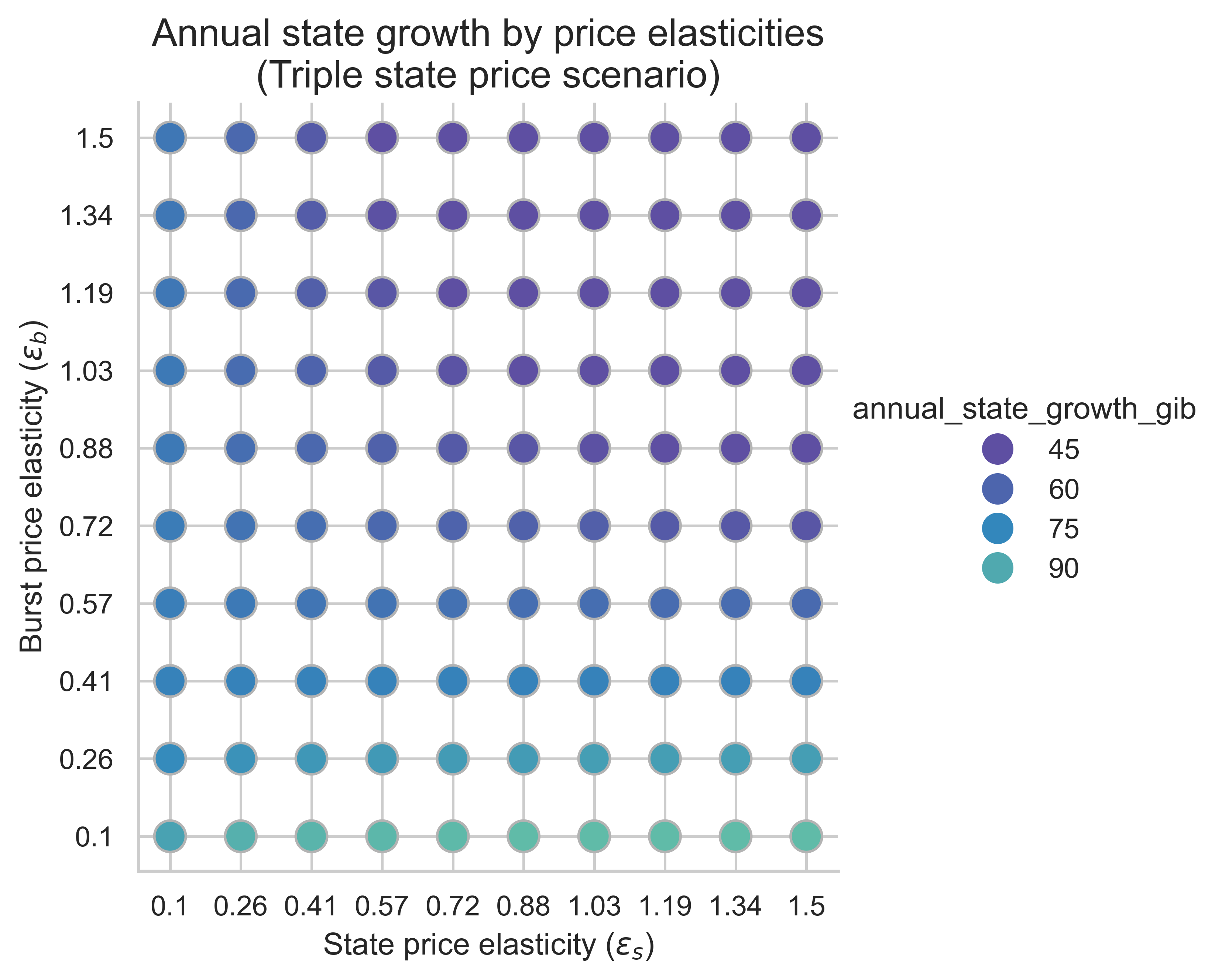
Không có gì ngạc nhiên khi việc tăng chi phí hoạt động tạo lập trạng thái làm giảm tốc độ tăng trưởng trạng thái trên tất cả các chế độ co giãn so với kịch bản không định giá lại. Điều này cho thấy việc tăng chi phí khí đốt cho việc tạo lập trạng thái có hiệu quả trong việc giảm thiểu tăng trưởng trạng thái trên một phạm vi rộng các độ co giãn giá.
Việc tăng chi phí khí đốt để tạo trạng thái còn có một tác động thú vị khác. Chúng ta có thể quan sát điều này bằng cách vẽ biểu đồ tăng trưởng trạng thái hàng năm so với độ co giãn cầu trạng thái \varepsilon_s ε s cho mỗi kịch bản. Sự thay đổi trên mỗi biểu đồ hộp là do độ co giãn cầu bùng nổ \varepsilon_b ε b .
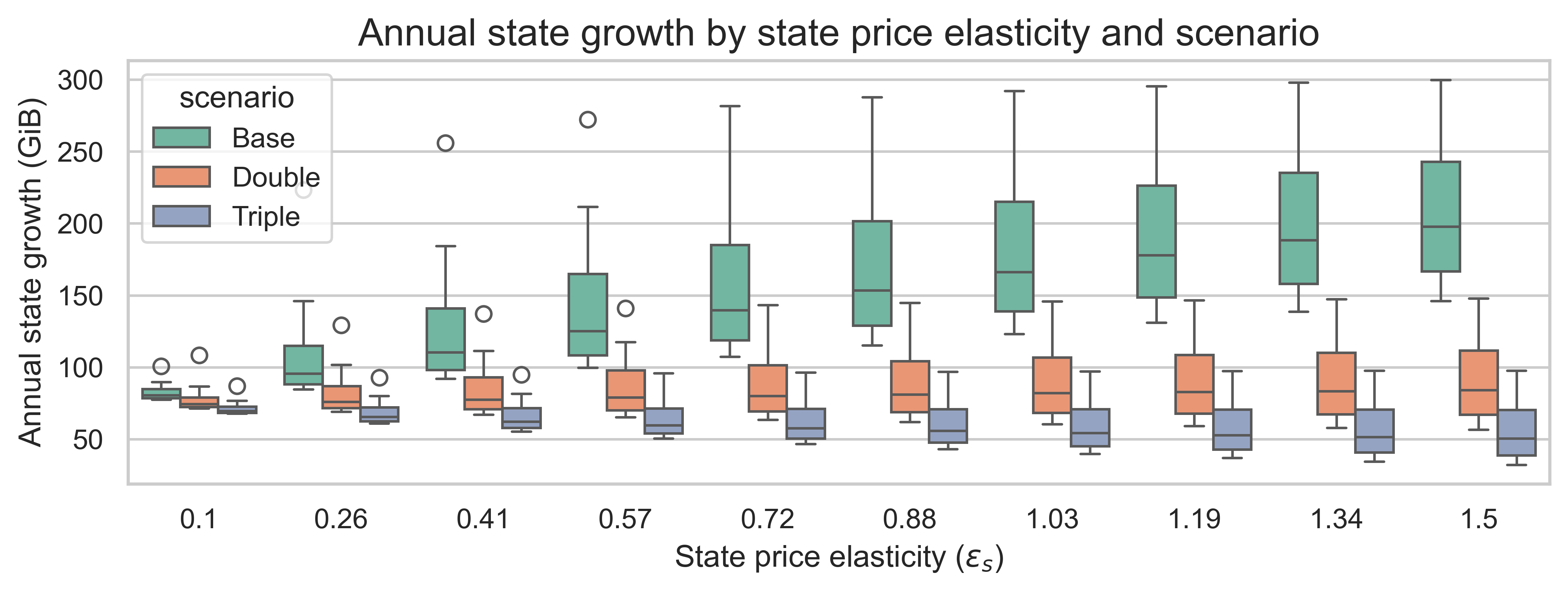
- Không định giá lại: \varepsilon_s cao hơn \ngụ ý ε s ⟹ tăng trưởng nhà nước nhiều hơn
- Định giá lại bằng với mức tăng giới hạn khối: \varepsilon_s cao hơn \ngụ ý ε s ⟹ không có thay đổi về mức tăng trưởng trung bình của tiểu bang
- Định giá lại cao hơn mức tăng giới hạn khối: \varepsilon_s cao hơn \ngụ ý ε s ⟹ tăng trưởng nhà nước ít hơn
Chúng ta nên lưu ý rằng độ co giãn nhu cầu của các nguồn tài nguyên bùng nổ cũng ảnh hưởng đến sự tăng trưởng của trạng thái: độ co giãn càng thấp thì tốc độ tăng trưởng của trạng thái càng cao trong mọi tình huống.
3.4 Tác động của việc định giá lại đối với thông lượng của các tài nguyên bùng nổ
Các biểu đồ sau đây cho thấy mức tăng thông lượng trên các tài nguyên bùng nổ trong khối cân bằng cho tất cả các kết hợp độ co giãn giá (\varepsilon_s, \varepsilon_b) ( ε s , ε b ) . Độ lợi được tính toán dựa trên thông lượng cơ sở 0,7 giây.
Chỉ số này rất quan trọng để đo lường tác động của việc tăng chi phí tạo trạng thái lên khả năng mở rộng. Nếu chúng ta tăng gấp đôi lượng gas khả dụng, liệu chúng ta có vẫn quan sát được ít nhất gấp đôi thông lượng cho tài nguyên burst không? Hãy nhớ rằng thông lượng cơ sở là 0,7 giây.
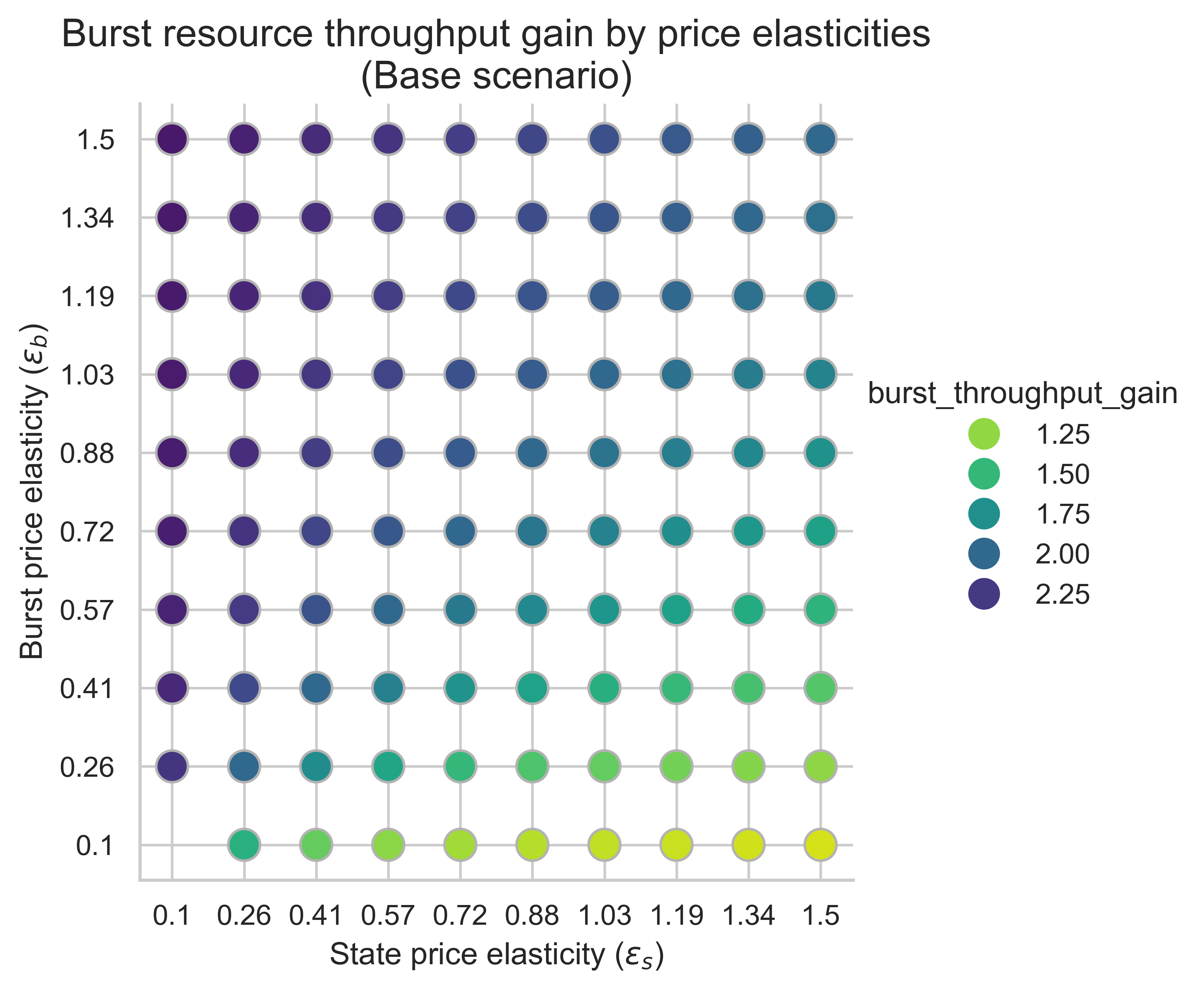
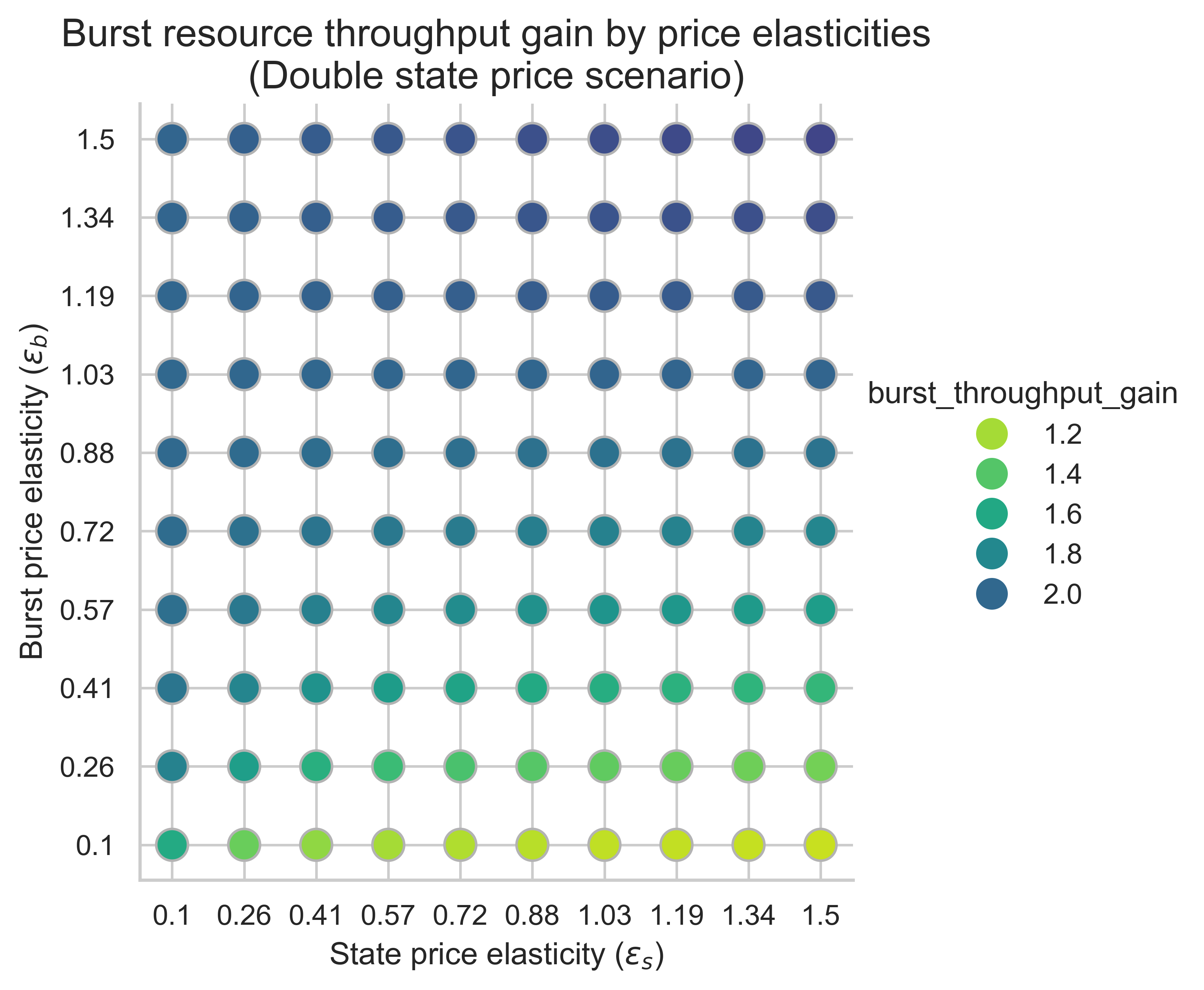
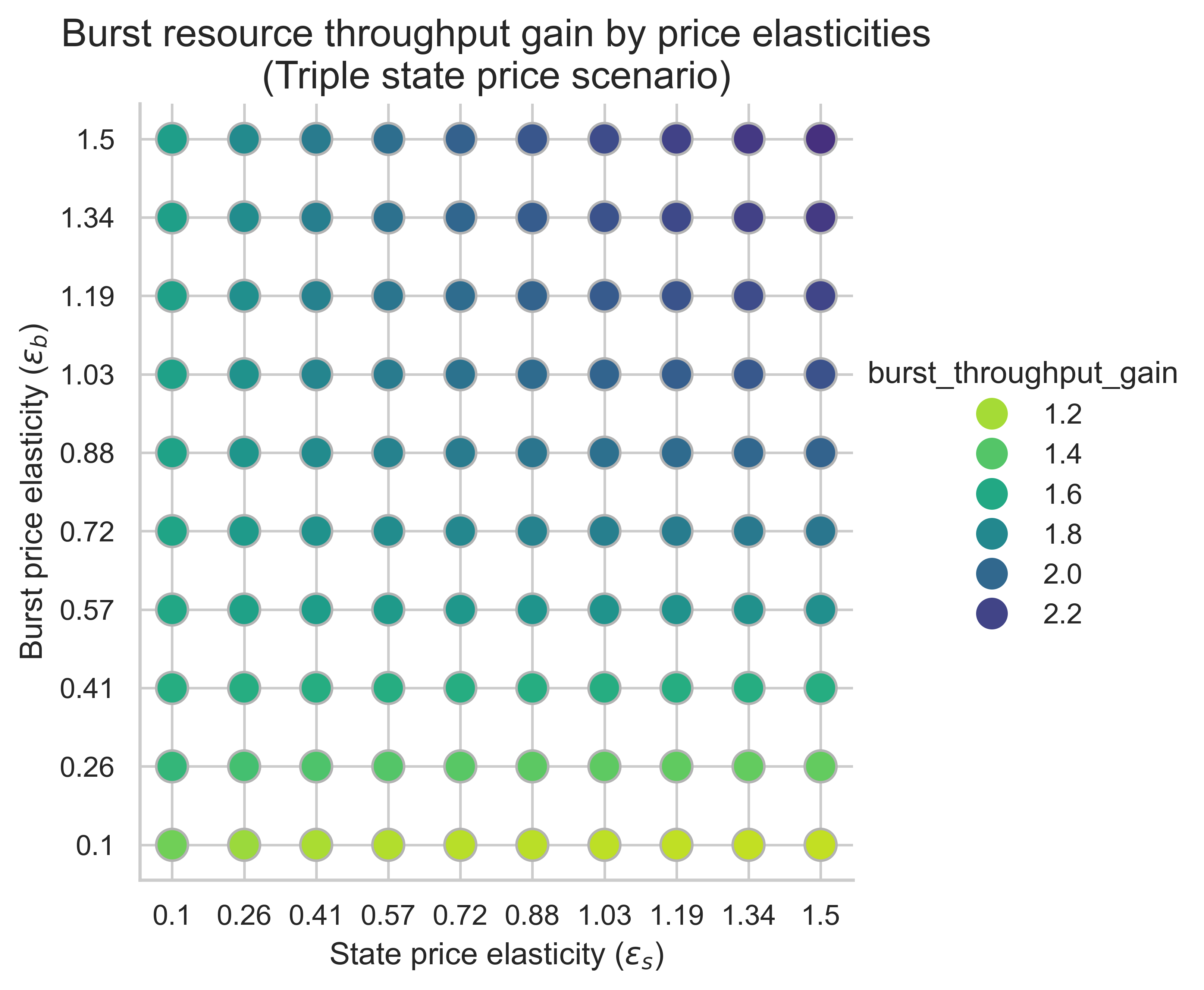
Trong cả ba kịch bản, động lực chính của mức tăng thông lượng bùng nổ là độ co giãn giá phía bùng nổ, \varepsilon_b ε b . Khi \varepsilon_b ε b tăng, chúng ta thấy mức tăng ngày càng tăng so với đường cơ sở 0,7 giây:
- Khi nhu cầu bùng nổ đủ linh hoạt theo giá (phía trên của biểu đồ), công suất tăng gấp đôi sẽ chuyển thành thông lượng bùng nổ tăng gấp đôi (hoặc hơn một chút).
- Khi nhu cầu bùng nổ không co giãn (phía dưới của biểu đồ), công suất tăng gấp đôi sẽ tương đương với thông lượng bùng nổ ít hơn gấp đôi.
Ngược lại, biến thiên theo chiều ngang với độ co giãn trạng thái \varepsilon_s ε s phức tạp hơn. Mức tăng giảm nhẹ khi \varepsilon_s ε s tăng khi m = 1 m = 1. Đối với m = 2 m = 2 hoặc m = 3 m = 3 , mức tăng thông lượng cao nhất trên các tài nguyên burst đạt được khi cả hai độ co giãn giá đều cao.
Trong biểu đồ sau, chúng ta có thể thấy rõ hơn tác động của việc tăng chi phí tạo trạng thái lên thông lượng. Sự thay đổi trên mỗi biểu đồ hộp là do độ co giãn cầu trạng thái \varepsilon_s ε s .
Nhìn chung, chi phí cao hơn làm giảm nhẹ mức tăng thông lượng. Tuy nhiên, tác động này là nhỏ khi so sánh với tác động của độ co giãn cầu của tài nguyên burst. Nếu chúng ta đang ở trong chế độ có \varepsilon_b ε b cao, thì việc tăng cường tạo trạng thái sẽ ảnh hưởng đến thông lượng ít hơn 25%.
3.5 Phí cân bằng
Chỉ số cuối cùng chúng ta muốn phân tích là phí cơ sở cân bằng. Chúng tôi kỳ vọng mức phí này sẽ thấp hơn mức cơ sở b^0=1 b 0 = 1. Tuy nhiên, mức phí này sẽ giảm bao nhiêu trong các chế độ đàn hồi và định giá lại khác nhau? Biểu đồ sau đây cho thấy phí cơ sở cân bằng cho ba kịch bản định giá lại và độ co giãn cầu bùng nổ. Sự thay đổi trên mỗi biểu đồ hộp là do độ co giãn cầu trạng thái \varepsilon_s ε s .
Trong cả ba kịch bản định giá, phí cơ sở cân bằng tăng theo độ co giãn giá phía bùng nổ: chuyển từ nhu cầu bùng nổ rất kém co giãn ( \varepsilon_b\approx0.1 ε b ≈ 0.1 ) sang cực kỳ co giãn ( \varepsilon_b\approx1.5 ε b ≈ 1.5 ) làm tăng gần gấp ba lần phí cơ sở trung vị. Khi độ co giãn cao, nhu cầu sẽ tăng lên để lấp đầy lượng khí có sẵn, do đó dẫn đến phí cơ sở cao hơn.
Độ co giãn cầu của nhà nước thì sao? Biểu đồ sau đây cho thấy mức phí cơ sở cân bằng cho ba kịch bản định giá lại và độ co giãn cầu của nhà nước. Sự thay đổi trên mỗi biểu đồ hộp là do độ co giãn cầu bùng nổ \varepsilon_b ε b .
Điều thú vị là chúng tôi không thấy mối quan hệ tuyến tính tương tự giữa phí cơ sở và nhu cầu của tiểu bang, với phí cơ sở trung vị duy trì phạm vi tương tự, bất kể độ co giãn của nhu cầu của tiểu bang. Tuy nhiên, chế độ co giãn có tác động đến thứ tự trong các kịch bản:
- Khi cầu trạng thái không co giãn (phía bên trái của biểu đồ), giá trạng thái cao hơn dẫn đến phí cân bằng cao hơn. Trong trường hợp này, việc làm cho trạng thái đắt hơn không ảnh hưởng nhiều đến cầu, do đó, lượng khí đốt được sử dụng nhiều hơn cho cùng một nhu cầu trạng thái.
- Khi cầu trạng thái co giãn (phía bên phải của đồ thị), giá trạng thái cao hơn dẫn đến phí cân bằng thấp hơn. Trong trường hợp này, nhu cầu tạo ra trạng thái phản ứng mạnh mẽ hơn với sự gia tăng chi phí trạng thái, do đó làm giảm phí cơ sở.
4. Thảo luận và các bước tiếp theo
Bài học đầu tiên rút ra là, theo mô hình đơn giản hóa của chúng tôi, việc tăng chi phí cho các hoạt động tạo trạng thái sẽ làm giảm đáng kể sự tăng trưởng của trạng thái trên tất cả các chế độ co giãn giá. Đơn giản là không có đủ khí để tăng trưởng trạng thái nhiều như trong kịch bản định giá cơ sở. Tuy nhiên, điều này vẫn đi kèm với chi phí tăng thông lượng thấp hơn một chút đối với các tài nguyên bùng nổ. Hiệu ứng này còn phức tạp hơn bởi độ co giãn của nhu cầu đối với các tài nguyên bùng nổ — chúng càng co giãn thì mức tăng thông lượng đạt được trên tất cả các kịch bản định giá càng cao. Nếu nhu cầu tạo trạng thái không co giãn, việc tăng chi phí tạo trạng thái dự kiến sẽ dẫn đến mức phí cơ sở cao hơn so với kịch bản trạng thái không được định giá lại.
Một câu hỏi tự nhiên là hệ thống thực sự nằm ở đâu trong lưới (\varepsilon_s,\varepsilon_b) ( ε s , ε b ) . Phân tích thực nghiệm sơ bộ của chúng tôi cho thấy nhu cầu tạo trạng thái trong ngắn hạn là khá kém co giãn: mức tăng 1% trong phí cơ sở tính bằng USD chỉ liên quan đến mức giảm ~0,6% trong trạng thái mới được tạo ra trên mỗi đơn vị khí trong những ngày tiếp theo. Được diễn giải thông qua lăng kính đẳng đàn hồi, điều này chỉ ra \varepsilon_s \approx 0,6 ε s ≈ 0,6 cho khối lượng công việc tạo trạng thái tổng hợp trong ngắn hạn. Điều đó phù hợp với trực giác rằng nhiều hành động nặng về trạng thái (mở vị thế, tạo hợp đồng, đúc mã thông báo, cam kết dữ liệu để cuộn lên, v.v.) được thúc đẩy bởi các quyết định kinh tế tồn tại lâu dài và các chính sách cấp giao thức không điều chỉnh ngay lập tức theo những thay đổi về giá. Chúng ta nên nói thêm rằng các hợp đồng spam như XEN dự kiến sẽ tạo ra mức giá sàn, vì bất cứ khi nào tổng chi phí tạo trạng thái giảm xuống dưới một ngưỡng nhất định, bot sẽ tràn vào mạng bằng các giao dịch có nhiều trạng thái, do đó làm tăng phí cơ sở cho các khối trong tương lai.
Đối với các nguồn lực bùng nổ, chúng tôi vẫn chưa có ước tính tương đương, nhưng có lý do để kỳ vọng độ đàn hồi cao hơn, ít nhất là đối với một phần lớn khối lượng công việc. Nhiều hoạt động bị chi phối bởi bùng nổ (chênh lệch giá, thanh lý, tìm kiếm MEV, giao dịch nhạy cảm với độ trễ) rõ ràng bị ràng buộc về phí và có thể nhanh chóng giảm xuống.
