Mở đầu
Trong ngữ cảnh blockchain, zk-SNARK là một công nghệ bảo mật tiên tiến giúp tăng cường quyền riêng tư và đảm bảo tính minh bạch trong các giao dịch mã hóa.
Zk-SNARK cho phép chứng minh một kiến thức mà không cần tiết lộ kiến thức đó, giữ cho thông tin của người dùng được bảo vệ một cách tuyệt đối.
Zcash, một đồng tiền mã hóa hàng đầu, sử dụng công nghệ zk-SNARK để ẩn danh hoàn toàn các giao dịch, đảm bảo tính bảo mật cao và không để lộ thông tin cá nhân của người dùng. Điều này làm tăng tính an toàn và tin cậy cho người dùng khi thực hiện các giao dịch trực tuyến.
Đối với phần 1 trong chuỗi nghiên cứu “Khám phá ZK-SNARK” , mình sẽ đi sâu vào các chi tiết quan trọng về zk-SNARKs cũng như các thuật toán và mã hóa cơ bản đằng sau công nghệ này một cách chi tiết và dễ hiểu cho các bạn nhé.
Khái niệm và cơ chế hoạt động của zk-SNARK
Khái niệm cơ bản về zk-SNARK
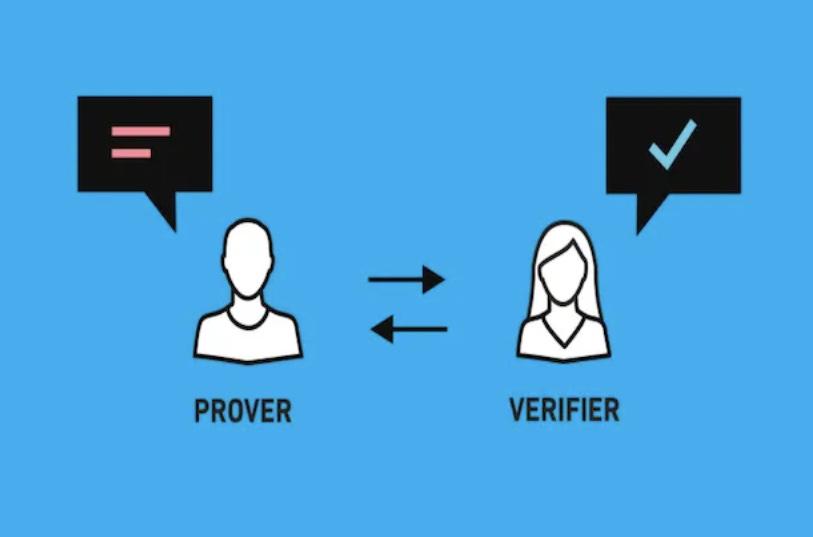
Zk-SNARK là viết tắt của Zero-Knowledge Succinct Non-Interactive Argument of Knowledge, tạm dịch là “Chứng minh không tiết lộ kiến thức một cách ngắn gọn và không tương tác“(Mình dịch như vậy cho dễ hiểu). Đây là một cách xây dựng chứng minh cho phép một bên (người chứng minh) chứng minh rằng họ sở hữu một thông tin nhất định, ví dụ như một khóa bí mật, mà không cần phải tiết lộ thông tin đó và không cần tương tác với một bên khác (người xác minh).
Hiện tại, zk-SNARK là hệ thống bằng chứng phổ biến nhất đang được sử dụng.
Ta sẽ chia từ viết tắt “zk-SNARK” thành các thành phần nhỏ hơn để xem xét ý nghĩa của chúng 1 cách rõ ràng nhất.
- “Zero-Knowledge”(Kiến thức bằng 0): Điều này có nghĩa là những thông tin đầu vào sẽ bị ẩn đi và không được tiết lộ cho người xác minh. Nói cách khác, người xác minh không thể biết bất kì điều gì về kiến thức đó mà chỉ biết tính hợp lệ của kiến thức đó.
- “Succinct”(Ngắn gọn): Điều này nghĩa là các bằng chứng được tạo ra có kích thước nhỏ, khoảng vài trăm byte và được xác minh nhanh chóng. Đây chính là lợi ích đầu tiên mà SNARK mang lại.
- “Non-interactive”(Không tương tác): Đây chính là lợi ích thứ 2 của SNARK, cả 2 bên(người chứng minh và người xác minh), bằng chứng bao gồm một tin nhắn duy nhất từ người chứng minh đến người xác minh mà không cần giao tiếp qua lại.
- “Argument of knowledge”(Lập luận về kiến thức): Là một thuật ngữ kỹ thuật có nghĩa là nếu người xác minh chấp nhận một bằng chứng thì người chứng minh thực sự phải biết một bí mật liên quan đến tuyên bố đang được chứng minh (thay vì chỉ thuyết phục người xác minh rằng tuyên bố đó là đúng).
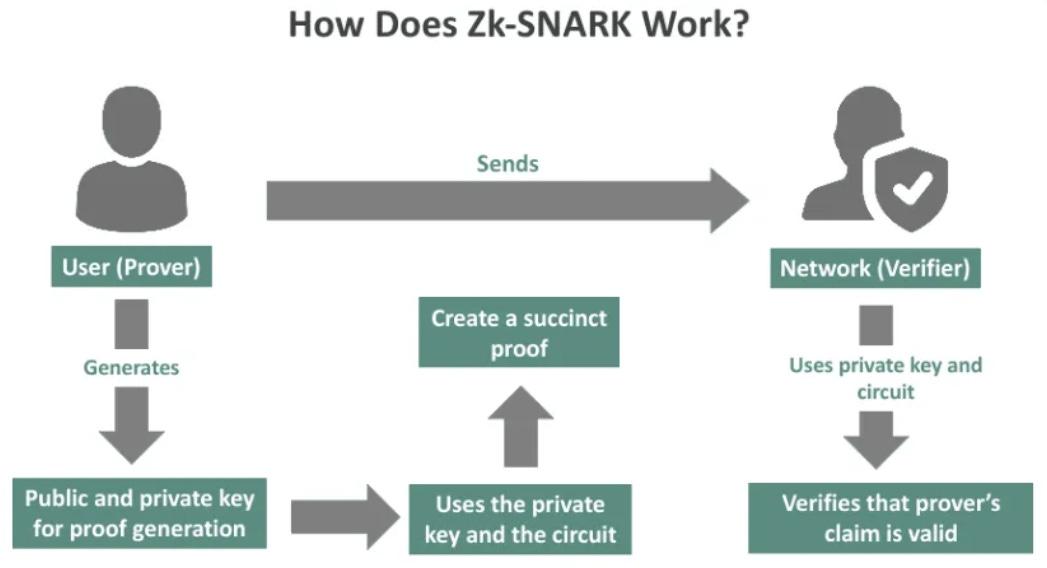
Cơ chế hoạt động
Về mặt toán học, zk-SNARK bao gồm 3 thuật toán:
- Key Generation(KG): Đây là thuật toán tạo khóa, sẽ tạo ra một cặp khóa, một để chứng minh (pk) và một để xác minh (vk). Thuật toán tạo khóa lấy đầu vào là tham số bảo mật λ và chương trình C, sau đó xuất ra các khóa. Bước này còn gọi là bước Trusted Setup. Ta sẽ đi vào chi tiết của nó trong phần bên dưới.(pk, vk) = KG(λ, C)
- Proving(P): Thuật toán chứng minh này sẽ chứng minh bằng cách lấy đầu vào là khóa chứng minh pk, một câu lệnh x và một nhân chứng w. Đầu ra là một bằng chứng prf.prf = P(pk, x, w)
- Verification(V): Thuật toán xác minh lấy đầu vào là khóa xác minh vk, câu lệnh x và bằng chứng prf. Đầu ra là chấp nhận hoặc từ chối.
VerificationResult = V(vk, x, prf)
Lợi ích của ZK-SNARKs
- ZK-SNARKs mang lại nhiều lợi ích quan trọng, đặc biệt trong việc tăng cường tính ẩn danh, bảo mật, khả năng mở rộng và hiệu quả giao dịch trong nhiều ứng dụng khác nhau. Dưới đây là 2 lợi ích chính cho các ứng dụng phần mềm:
- Quyền riêng tư(Privacy): thuộc tính “zero-knowledge” cho phép ẩn dữ liệu nhạy cảm liên quan đến các tính toán trong khi vẫn chứng minh tính đúng đắn của tuyên bố. Nói cách khác, zk-snark thực hiện giao dịch mà không cần tiết lộ thông tin cá nhân, giữ thông tin giao dịch ẩn danh và bảo mật. Điều này rất hữu ích trong các đồng tiền mã hóa như Zcash, nơi người dùng có thể gửi tiền mà không cần tiết lộ số lượng, nguồn gốc hoặc điểm đến của các giao dịch.
- Khả năng mở rộng(Scalability): Nhờ vào kích thước chứng minh nhỏ và thời gian xác minh ngắn cho phép người xác minh nhanh chóng biết rằng tính toán được thực hiện một cách trung thực mà không cần phải chạy lại tính toán, từ đó giảm thời gian và tài nguyên cần thiết cho việc xác minh các tính toán phức tạp, giúp tăng hiệu suất và độ tin cậy của hệ thống, đồng thời giúp giảm chi phí và tăng cường khả năng mở rộng của nó.
Trusted setup ceremony (Quá trình thiết lập đáng tin cậy)
Quy trình thiết lập đáng tin cậy là một bước quan trọng được thực hiện một lần duy nhất để sinh ra một bộ dữ liệu cần thiết, được sử dụng sau này mỗi khi các giao thức mật mã được triển khai.
Trong ZK-SNARK, bước thiết lập đáng tin cậy này là cần thiết để tạo ra các khóa chứng minh và xác minh. Những khóa này sau đó được công bố công khai, cho phép các bên tham gia có thể sử dụng chúng để tạo ra và kiểm tra các bằng chứng.
Đối với mỗi chương trình C mới, một quá trình thiết lập đáng tin cậy mới cần phải được thực hiện vì nó tùy thuộc vào chi tiết của chương trình C đó. Trong quá trình thiết lập, quá trình sinh khóa KG sử dụng một lambda bí mật và chương trình C làm đầu vào để sinh ra khóa công khai (pk) và khóa xác minh (vk).
(pk, vk) = KG(λ, C)
Vì vậy, quy trình thiết lập đáng tin cậy không phải là tiêu chuẩn chung và cần được tiến hành riêng biệt cho mỗi chương trình mới.
Toxic Waste (Chất thải độc hại)
Một tham số bí mật gọi là lamda là cần thiết cho quá trình thiết lập đáng tin cậy. Tham số này, thường được gọi là “Toxic Waste“, đôi khi gây khó khăn khi áp dụng zk-SNARK vào các ứng dụng thực tế.
Điều này là do bất cứ ai nắm giữ thông số này có khả năng tạo ra các bằng chứng giả. Cụ thể, người nắm giữ lambda có thể tạo ra một bằng chứng giả, gọi là fakeProof, cho bất kỳ chương trình C nào với các đầu vào công khai x, sao cho
V(vk,x,fakeProof)=true
được đánh giá là đúng mà không cần biết nhân chứng bí mật w. Điều này thật tai hại!
Cách hiệu quả nhất để tạo ra các tham số công khai cho zk-SNARK là thông qua việc một ai đó sinh ra một cặp khóa công khai và khóa bí mật, tương tự như cặp khóa ECDSA, rồi sau đó tiêu hủy khóa bí mật. Tuy nhiên, điểm băn khoăn là làm thế nào để chúng ta có thể chắc chắn rằng bên này đã thực sự loại bỏ những “chất thải độc hại” đó?
Do đó, để giải quyết vấn đề này, Tính toán Đa bên (Multi-Party Computation, MPC) được áp dụng.
MPC là một giao thức mật mã cho phép nhiều bên tham gia tính toán một cách phân tán mà không bên nào có quyền truy cập vào dữ liệu bí mật của bên khác.
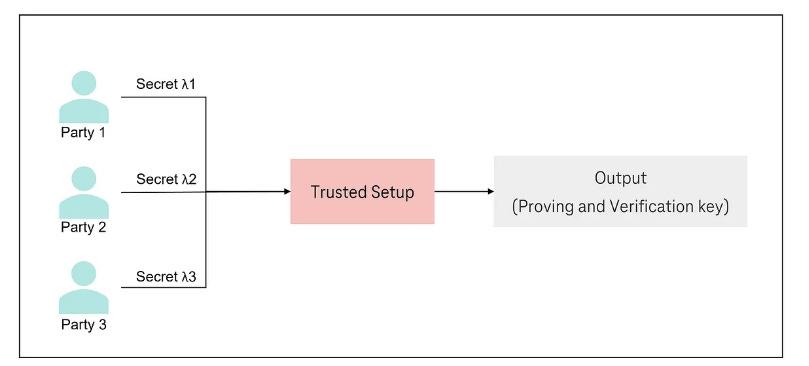
Trong mỗi quy trình thiết lập đáng tin cậy, nhiều bên cùng nhau tham gia vào quá trình để tạo ra các thành phần mật mã cần thiết, như khóa công khai (pk) và khóa xác minh (vk). Mỗi bên đóng góp một phần dữ liệu bí mật của mình vào quá trình này.
Mục tiêu cuối cùng của mỗi bên sau quá trình này là phải loại bỏ hoàn toàn các chất thải độc hại. Giả định về độ tin cậy trong trường hợp này là chỉ cần một trong số n bên tham gia là trung thực, thì kết quả cuối cùng sẽ được đảm bảo an toàn.
Trong quá trình thiết lập đáng tin cậy, mỗi trong số n bên đem theo lambda bí mật của họ để cùng tạo nên các khóa chứng minh và xác minh.
Để quá trình thiết lập này thất bại, điều đó đòi hỏi tất cả n bên phải cùng có ý đồ xấu và chia sẻ bí mật của mình với nhau. Tuy nhiên, chỉ cần một trong số các bên quyết định không tiết lộ bí mật của họ, quá trình thiết lập đáng tin cậy vẫn sẽ diễn ra thành công, làm cho việc sản xuất các bằng chứng giả không thể xảy ra.
Cơ sở toán học và mã hóa đằng sau zk-snark
Mathematical foundations (Cơ sở toán học)
Group theory (Lý thuyết nhóm)
ZK-SNARK tận dụng lý thuyết nhóm trong việc thực hiện các phép tính trên elliptic curves và các nhóm khác, nhất là khi sử dụng các bilinear pairings và thuật toán liên quan.
Đơn giản mà nói, một nhóm là một tập hợp các phần tử {a, b, c, …} kết hợp với một phép toán nhị phân, mà ở đây chúng ta ký hiệu là “•”.
Một tập hợp và phép toán được gọi là nhóm nếu chúng thỏa mãn các tính chất sau:
- Tính đóng (Closure): Đối với mọi a và b thuộc nhóm G, phép toán a • b cũng phải thuộc G.
- Tính kết hợp (Associativity): Đối với mọi a, b, và c thuộc G, phép toán (a • b) • c phải bằng a • (b • c).
- Phần tử đơn vị (Identity Element): Phải có một phần tử e trong G sao cho với mọi phần tử a trong G, phép toán e • a và a • e đều bằng a. Phần tử này là duy nhất.
- Phần tử nghịch đảo (Inverse Element): Đối với mỗi phần tử a trong G, phải có một phần tử b trong G, thường được gọi là a^-1, sao cho phép toán a • b và b • a đều bằng phần tử đơn vị e.
Subgroups
Khi một tập hợp con của các phần tử trong một nhóm tuân theo tất cả các tính chất của nhóm, tập hợp đó được gọi là nhóm con của nhóm ban đầu.
Fields
Trường là một cấu trúc đại số đặc biệt, nơi một tập hợp các phần tử thực hiện hai phép toán cơ bản: phép cộng và phép nhân. Mỗi trường phải tuân thủ một loạt các tiên đề cơ bản, giúp định nghĩa và đảm bảo các tính chất chung của nó.
Dưới đây là các tiên đề mà một trường phải thỏa mãn, với a, b, và c là các phần tử bất kỳ của trường F:
- Tính kết hợp của phép cộng và phép nhân : a + (b + c)= (a + b) + c vàa · (b · c) = (a · b) · c
- Tính giao hoán của phép cộng và phép nhân : a + b = b + a và a · b = b · a
- Đẳng thức cộng và nhân : Tồn tại hai phần tử 0 và 1 khác nhau trong F sao cho a + 0 = a và a · 1 = a
- Nghịch đảo cộng : Với mọi a trong F, tồn tại một phần tử trong F, ký hiệu −a, được gọi là nghịch đảo cộng của a sao cho a + (−a) = 0
- Nghịch đảo của phép nhân : Với mọi a≠ 0 thuộc F, tồn tại một phần tử trong F, ký hiệu là a^ -1, gọi là nghịch đảo nhân của a sao cho a · a^ -1 = 1
- Phân phối của phép nhân đối với phép cộng : a· (b + c) = (a · b) + (a · c)
Các ví dụ về trường bao gồm tập hợp các số thực với phép cộng và phép nhân, cũng như các số nguyên modulo một số nguyên tố, nơi cả phép cộng và phép nhân đều được định nghĩa.
Finite fields
Trong ZK-SNARK, mọi phép toán đều được thực hiện trong các trường hữu hạn (finite fields), nơi giá trị và phép toán được xác định dưới modulo một số nguyên tố hoặc dựa trên một đa thức nguyên tố.
Một trường hữu hạn là một trường có số lượng phần tử hữu hạn, ví dụ như tập hợp các số nguyên modulo p, với p là số nguyên tố.
Số phần tử trong một trường, được gọi là thứ tự của trường, đối với trường hữu hạn có thể là:
- Một số nguyên tố (trường nguyên tố)
- Hoặc một lũy thừa của số nguyên tố (trường mở rộng)
Trong trường nguyên tố đơn giản, một phần tử có thể được biểu diễn bằng một số nguyên từ 0 đến p-1, nơi Zp = {0, 1, …, p-1}.
Phần mở rộng của Zp, được gọi là nhóm nhân Zp*, bao gồm các phần tử nguyên tố cùng nhau với p, tức là Zp* = {1, …, p-1}.
Generators of finite fields
Trong mỗi trường hữu hạn, luôn tồn tại một phần tử gọi là generator, có khả năng tạo ra tất cả các phần tử trong nhóm bằng cách sử dụng phép lũy thừa của nó.
Ví dụ, xét nhóm Z5* trong trường nguyên tố Z5 = {0, 1, 2, 3, 4}, khi đó Z5* = {1, 2, 3, 4}. Trong nhóm Z5*, phép nhân là phép toán nhị phân và các phép nhân được thực hiện theo modulo 5; chẳng hạn, phép nhân 3 × 4 không cho kết quả là 12 mà là 2, do 12 mod 5 = 2.
Nhóm Z5* là tuần hoàn và có các sinh là 2 và 3, bởi vì:
- Với generator 2, ta có:
2^0 = 1,
2^1 = 2,
2^2 = 4,
2^3 = 3,
2^4 = 1 (lặp lại chu kỳ)
- Và với generator 3, ta có:
3^0 = 1,
3^1 = 3,
3^2 = 4,
3^3 = 2,
3^4 = 1 (lặp lại chu kỳ)
Những tính chất này làm cho Z5* trở thành một nhóm mạnh mẽ cho các phép toán mật mã, và nó thường được sử dụng trong các thuật toán mật mã như ZK-SNARKs.
Group homomorphisms
Homomorphisms là những ánh xạ giữa hai cấu trúc đại số tương tự nhau, chẳng hạn như nhóm hoặc trường, và chúng bảo toàn các phép toán trong cấu trúc đó.
Cụ thể, một phép đồng cấu là một ánh xạ f từ nhóm A sang nhóm B, khi hai nhóm này có cùng phép toán nhị phân, ví dụ như phép nhân hoặc phép cộng. Ánh xạ này bảo toàn phép toán, có nghĩa là:
Nếu ⋅ là phép toán nhị phân trong cấu trúc của nhóm A và B, thì cho mọi phần tử a và b trong nhóm A, ánh xạ f thỏa mãn điều kiện:
f ( x ⋅ y )= f ( x )⋅ f ( y )
Điều này đảm bảo rằng kết quả của phép toán khi áp dụng cho các phần tử trong nhóm A, sau khi được ánh xạ sang nhóm B thông qua f, vẫn giữ nguyên tính chất tương đương với phép toán đã thực hiện trực tiếp trên nhóm B.
Homomorphisms chính là nền tảng để xử lý các tính chất của bilinear pairings, làm cho quá trình tạo và xác minh các bằng chứng trong zk-SNARK trở nên hiệu quả hơn.
Polynomials
Đa thức là thành phần cốt lõi trong việc xây dựng Quadratic Arithmetic Programs (QAPs), nơi mà các bài toán được biểu diễn qua các đa thức và giải quyết thông qua việc đánh giá và cam kết đa thức.
Đa thức là biểu thức toán học tạo nên từ các biến và hằng số, sử dụng các phép cộng, nhân và lũy thừa với số mũ nguyên không âm.
Chẳng hạn, đa thức 5x² + 2x + 8 là một ví dụ điển hình.
Khi xét đến một phương trình đa thức, nó có thể đại diện cho vô số phương trình khác nhau giữa các số. Ví dụ, nếu ta có phương trình A(x) + B(x) = C(x) mà đúng, thì nó cũng sẽ đúng tại mọi giá trị của x, như:
A(0) + B(0) = C(0)
A(1) + B(1) = C(1)
A(2) + B(2) = C(2)
A(3) + B(3) = C(3)
và tiếp tục như vậy.
Về bậc của đa thức, nó được xác định bởi lũy thừa lớn nhất của biến trong đa thức. Ví dụ, đa thức 6x⁴ + 2x³ + 3 có bậc là 4, vì lũy thừa cao nhất của biến x là 4.
Crytography (Mật mã)
Hash functions
Các hàm băm được sử dụng rộng rãi để tạo ra các “cam kết” trong các giao thức mã hóa, giúp đảm bảo rằng dữ liệu không thể bị chỉnh sửa mà không được phát hiện.
Hàm băm là một thuật toán hoặc hàm toán học chuyển đổi một chuỗi dữ liệu đầu vào có độ dài thay đổi thành một chuỗi đầu ra có độ dài cố định, được gọi là giá trị băm.
Công thức biểu diễn hàm băm có thể được mô tả như sau:
f ( m )= H
trong đó f là hàm băm, m là thông điệp, và H là giá trị băm thu được.
Các hàm băm có nhiều đặc tính quan trọng, làm cho chúng trở nên rất hữu ích trong nhiều ứng dụng mã hóa. Các thuộc tính đó bao gồm:
- Pre-image resistance: Về mặt toán học, việc tìm lại thông điệp ban đầu từ giá trị băm là rất khó.
- Second pre-image resistance: Với một thông điệp đầu vào cụ thể và giá trị băm của nó, rất khó để tìm một thông điệp khác mà cho ra cùng một giá trị băm.
- Collision resistance: Khó để tìm hai thông điệp khác nhau sao cho chúng cho ra cùng một giá trị băm.
Một đặc tính rất đáng mong đợi của các hàm băm tốt là Avalanche Effect. Đây là tính chất mà theo đó một thay đổi nhỏ ở đầu vào sẽ gây ra thay đổi lớn ở đầu ra, khiến đầu ra có vẻ ngẫu nhiên và không thể phân biệt được.
Encryption
Một cách đơn giản, mã hóa là quá trình chuyển đổi thông điệp đầu vào (bản rõ) thành đầu ra có vẻ ngẫu nhiên (bản mã), sao cho chỉ những người có quyền mới có thể giải mã và hiểu thông tin đó. Quá trình mã hóa dựa trên việc sử dụng khóa mật mã, là một tập hợp các giá trị toán học mà cả người gửi và người nhận đều sử dụng để mã hóa và giải mã thông tin.
Có hai loại thuật toán mã hóa: Symmetric encryption (Mã hóa đối xứng) và Asymmetric encryption (Mã hóa bất đối xứng).
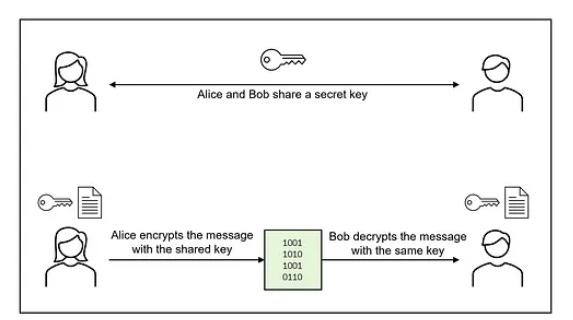
Symmetric encryption
Trong mã hóa đối xứng, cùng một khóa được sử dụng bởi tất cả các bên tham gia trong quá trình truyền thông để mã hóa và giải mã thông điệp. Khóa này được giữ bí mật giữa các bên để đảm bảo tính bảo mật của thông tin trao đổi.
Asymmetric encryption
Trong mã hóa bất đối xứng, hay còn gọi là mã hóa khóa công khai, có hai loại khóa: một khóa công khai dùng để mã hóa và một khóa riêng tư dùng để giải mã. Khóa riêng tư được giữ kín bởi người nhận (vì thế mới gọi là “khóa riêng”), trong khi khóa công khai có thể được chia sẻ rộng rãi với bất kỳ ai muốn gửi thông tin mật (vì thế được gọi là “khóa công khai”).
Mã hóa bất đối xứng được ứng dụng rộng rãi trong các tình huống sau:
- Gửi tin nhắn bảo mật: Người gửi sử dụng khóa công khai của người nhận để mã hóa thông điệp, sau đó gửi nó đến người nhận. Chỉ người nhận sở hữu khóa riêng mới có thể giải mã và đọc được thông điệp.
- Chứng minh quyền sở hữu (biết về) khóa riêng: Trong quá trình chứng minh quyền sở hữu khóa riêng, người gửi sẽ mã hóa (hoặc ký) tin nhắn bằng khóa riêng của mình và sau đó gửi tin nhắn đó đến người nhận. Người nhận sử dụng khóa công khai của người gửi để giải mã tin nhắn. Quá trình này thường được gọi là ký số, và tin nhắn đã được mã hóa như vậy được gọi là “chữ ký số“. Qua đó, chữ ký số chứng minh rằng tin nhắn được gửi bởi ai đó sở hữu khóa riêng tương ứng, đồng thời giúp xác minh tính toàn vẹn của thông tin trong tin nhắn.
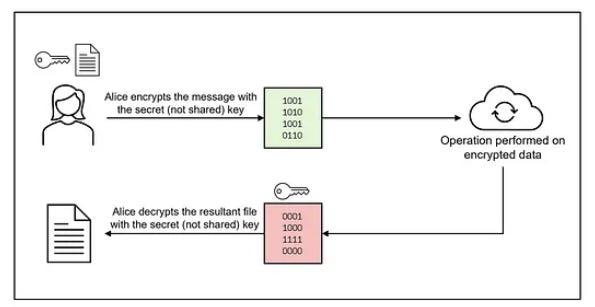
Homomorphic encryption (Mã hóa đồng cấu)
Mã hóa đồng cấu có ảnh hưởng lớn trong việc thiết kế các bằng chứng zero-knowledge ở cấp độ cao, bởi nó cho phép thực hiện các phép tính trên dữ liệu đã mã hóa mà không cần phải giải mã chúng.
Mã hóa đồng cấu là một loại mã hóa đặc biệt cho phép thực hiện các phép tính trực tiếp trên dữ liệu mã hóa. Điều này có nghĩa là có thể thực hiện các phép tính bổ sung trên dữ liệu đã mã hóa mà không cần đến khóa bí mật. Kết quả của các phép tính này vẫn ở dạng mã hóa, đảm bảo tính bảo mật mà không làm lộ nội dung dữ liệu gốc.
Trong thực tế, mã hóa đồng cấu hoàn toàn, cho phép thực hiện mọi loại phép tính tùy ý trên dữ liệu đã mã hóa, vẫn còn gặp nhiều hạn chế và chưa thể áp dụng rộng rãi. Tuy nhiên, việc thực hiện một số phép toán nhất định trên cấu trúc đồng cấu là khả thi và đã được sử dụng trong các ứng dụng thực tế.
Các thao tác này bao gồm phép cộng và nhân trên dữ liệu mã hóa, điều này đã mở ra những khả năng mới cho việc xử lý dữ liệu bảo mật mà không cần giải mã.
Elliptic Curve Cryptography (ECC)
Trong ZK-SNARK, đường cong elip đóng một vai trò quan trọng nhờ các thao tác nhóm mà trên đó thực hiện được pairing bilinear. ECC (Elliptic Curve Cryptography) cung cấp một nền tảng hiệu quả cho việc tạo và xác minh các bằng chứng zero-knowledge.
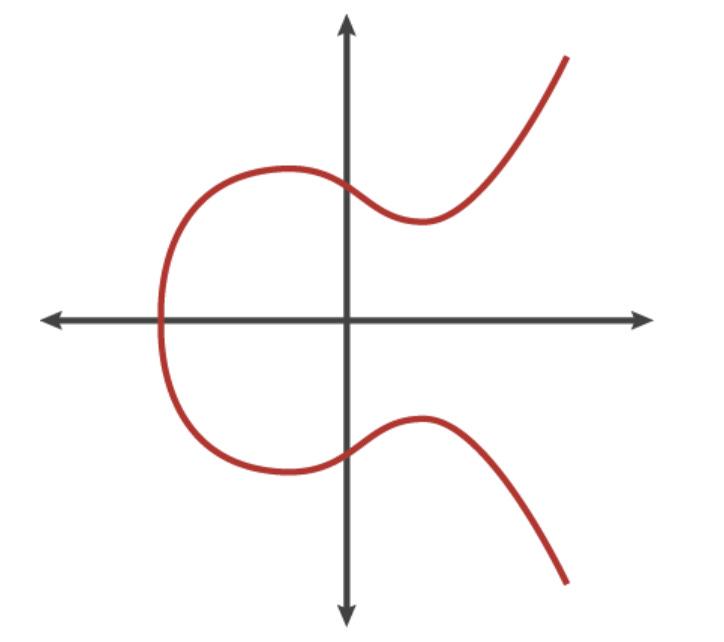
Một đường cong elip là tập hợp các điểm thỏa mãn một phương trình toán học cụ thể. Phương trình cho một đường cong elip có dạng như sau:
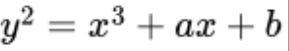
Trong đó, a và b là các hằng số đã biết. Đồ thị của phương trình này có dạng như sau:
Có nhiều biểu diễn khác nhau của các đường cong elip, nhưng kỹ thuật này chủ yếu là tìm ra các điểm thỏa mãn một phương trình toán học nhất định.
Các đặc tính của đường cong elip làm cho chúng trở nên rất quan trọng trong nhiều lĩnh vực toán học và đặc biệt trong lĩnh vực mật mã.
Một tính chất thú vị của đường cong elip là sự đối xứng theo chiều ngang. Bất kỳ điểm nào trên đường cong cũng có thể phản chiếu qua trục x mà vẫn giữ nguyên đường cong. Điều này có nghĩa là nếu bạn lấy hai điểm bất kỳ trên đường cong và vẽ một đường thẳng qua chúng, đường thẳng đó sẽ cắt đường cong ở một điểm thứ ba.
Thử tưởng tượng đây là một trò chơi bi-a , quả bóng được bắn từ một điểm và khi nó chạm vào đường cong elip, nó sẽ nảy thẳng lên hoặc thẳng xuống, tùy thuộc vào vị trí của nó so với trục x.
Một tính chất thú vị của đường cong elip là bạn có thể “chấm” hai điểm trên đường cong để tạo ra một điểm mới. Bạn cũng có thể liên tiếp “chấm” một điểm với chính nó để tạo ra các điểm khác nhau trên đường cong.
Nhưng điều thú vị là, nếu bạn biết điểm cuối cùng và điểm ban đầu, việc tính toán số lần “chấm” cần thiết để đi từ điểm ban đầu đến điểm cuối cùng là rất khó!
Thử tưởng tượng một người chơi một mình trong một phòng, đánh bóng theo quy tắc của trò chơi. Người khác sau đó vào và nhìn thấy vị trí cuối cùng của quả bóng. Ngay cả khi họ biết vị trí ban đầu và quy tắc của trò chơi, họ sẽ không thể biết được số lần bóng được đánh để đến đó mà không xem lại toàn bộ trò chơi từ đầu. Điều này tạo ra một tính chất đặc biệt trong mật mã học, gọi là tính không thể đảo ngược, và là cơ sở cho nhiều ứng dụng mạnh mẽ như Trapdoor Function.
Logarit rời rạc trên đường cong elip là một bài toán khó, làm nền tảng cho mật mã dựa trên đường cong elip. Không giống như phân tích nhân tử, không có lối tắt nào có thể giải quyết vấn đề này, làm cho việc phá vỡ mật mã đường cong elip khó hơn đáng kể so với RSA và Diffie-Hellman.
Mặc dù ECC mang lại mức độ bảo mật cao với các khóa ngắn hơn, nhưng vẫn giữ được hiệu suất tốt trên các thiết bị có công suất thấp. Điều này làm cho ECC trở thành lựa chọn lý tưởng cho các ứng dụng mật mã trên các thiết bị di động và các hệ thống có tài nguyên hạn chế.
Kết thúc phần này, mình đã nêu 1 số khái niệm toán học và mã hóa cơ bản đằng sau zk-SNARK, trong phần tiếp theo , mình sẽ nói rõ về các khái niệm nâng cao hơn như Quadratic Arithmetic Programs, Elliptic Curve Pairings.
Cảm ơn các bạn vì đã đọc tới đây. Nếu bạn thích bài viết này, đừng quên theo dõi và để lại một tràng pháo tay.
Nguồn bài viết: Team Tech/Research – AlphaTrue
Nguồn tham khảo:
1.Nguồn: Reitwiessner, C. (2016). zkSNARKs in a nutshell. Ethereum blog, 6, 1-15. https://chriseth.github.io/notes/articles/zksnarks/zksnarks.pdf
2. https://medium.com/coinmonks/from-zero-to-hero-in-zero-knowledge-proofs-part-7-61d639c2ef02
3. https://celo.academy/t/zk-snarks-proofs-as-a-privacy-solution-on-the-blockchain/1961
4.Nguồn: Chen, T., Lu, H., Kunpittaya, T., & Luo, A. (2022). A review of zk-snarks. arXiv preprint arXiv:2202.06877. https://arxiv.org/pdf/2202.06877.pdf
5. https://medium.com/coinmonks/from-zero-to-hero-in-zero-knowledge-proofs-part-8-262f923f1537
6. https://medium.com/@hira.siddiqui/from-zero-to-hero-in-zero-knowledge-proofs-part-2-ef17ce470f2d
7. Easttom, W. (2022). Modern cryptography: applied mathematics for encryption and information security. Springer Nature.
8. https://blog.cloudflare.com/a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/