Mở đầu
Ở phần trước, chúng ta đã cùng nhau tìm hiểu các kiến thức về cơ sở toán học và mã hóa đằng sau zk-SNARK một cách cơ bản. Bây giờ tôi sẽ tiếp tục đi sâu vào những khái niệm mới hơn và khá phức tạp, để các bạn có thể hiểu một cách sâu sắc hơn về công nghệ đằng sau zk-SNARK nhé!
Arithmetic Circuit (Mạch số học)
Khái niệm mạch số học
Mạch số học là một Directed Acyclic Graph(DAG) hay nói dễ hiểu là một biểu đồ tuần hoàn có hướng bao gồm:
- Các nút đóng vai trò như cổng cộng và nhân.
- Các cạnh đại diện cho dây dẫn, được thiết lập trên một trường hữu hạn Fp. Dây dẫn nối đầu ra của một cổng với đầu vào của cổng khác. Mỗi cổng có hai đầu vào và một đầu ra.
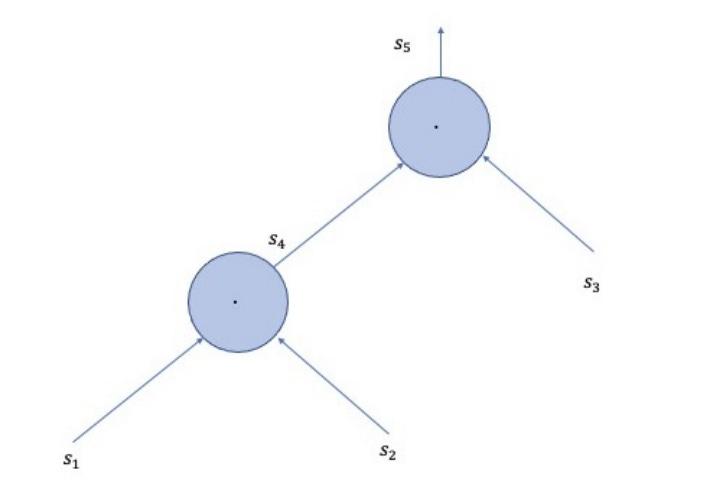
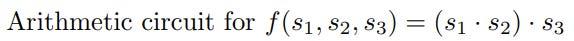
Mạch số học kết thúc với một đầu ra cuối cùng. Hình trên minh họa một ví dụ về mạch số học, nơi ta có thể thấy cách dữ liệu được xử lý và chuyển qua từng cổng để tạo ra kết quả cuối cùng.
Mạch số học cho ta biết về cách zk-SNARKs xử lý và chứng minh các tính toán mà không tiết lộ bất kỳ thông tin nào. Một mạch số học có thể được mô tả như một sơ đồ, nơi chứa các phép toán số học được sắp xếp một cách có hệ thống.
Hoạt động của Mạch số học
Xem xét hình trên, mạch số học cho phép chúng ta tính
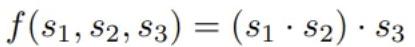
Nhìn vào hình trên, ta thấy quá trình này bắt đầu từ cổng nhân đầu tiên nhận s1 và s2 làm đầu vào và tạo ra s4 là đầu ra. Tiếp theo, s4 và s3 được đưa vào cổng nhân thứ hai để tạo ra đầu ra cuối cùng s5.
Đối với mạch m cổng, n dây, ta sẽ xác định được
witness s = (s1, s2, s3,…, sn)
để gán cho n dây của mạch sao cho đầu vào và đầu ra của mỗi cổng sẽ thỏa mãn ràng buộc được xác định bởi hoạt động của cổng.
Một mạch số học m cổng, n dây xác định mối quan hệ trên các nhân chứng
s = (s1, s2, …, sn)
sao cho đối với một hằng số

thì
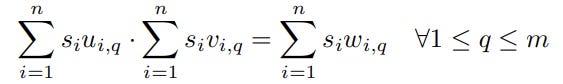
Những ràng buộc ở trên thuộc một tập hợp m các ràng buộc rank-1, có mục đích mô phỏng mối quan hệ giữa đầu vào và đầu ra của cổng nhân trong một mạch số học
Một ví dụ về ràng buộc rank-1 cụ thể là phương trình
s1 . s2 – s3 = 0.
Phương trình này mô tả một cổng nhân trong mạch, nơi lấy hai đầu vào s1 và s2, sau đó cho ra đầu ra là s3. Như vậy, sản phẩm của s1 và s2 phải bằng s3 để phương trình được thỏa mãn.
Một tập hợp m các ràng buộc rank-1 như thế này có thể được tổng quát hóa thành một Quadratic Arithmetic Program (Chương Trình Số học Bậc Hai).
QAPs chính là công cụ để chuyển đổi và giảm thiểu mạch số học xuống một dạng giúp dễ dàng hơn trong việc xác minh các phép toán mà không cần hiển thị lại toàn bộ mạch.
Quadratic Arithmetic Program
Cốt lõi của zk-SNARK nằm trong các Chương trình Đại số Bậc Hai (Quadratic Arithmetic Programs – QAPs). Một QAP có thể đại diện cho bất kỳ mạch số học nào, bao gồm các cổng cộng và nhân. Dựa trên một QAP, người chứng minh (prover) có thể tạo ra một bằng chứng cho thấy họ biết các giá trị đầu vào mà không tiết lộ gì về giá trị đó hay hành vi nội bộ của chương trình.
Nhà nghiên cứu zk-SNARK Eran Tromer đã vẽ quy trình xây dựng nên zk-SNARK từ các nguyên tắc cơ bản của toán học như sau:

Các bước ở trên có thể được chia thành hai nửa. Trong bài viết này sẽ giải thích sâu về “nửa đầu” của quy trình. “Nửa đầu” của quy trình có thể được xem xét là các bước từ “Computation” đến “QAP”, đây là phần nơi quá trình tính toán ban đầu được chuyển đổi thành một dạng toán học có thể sử dụng để thiết lập một zk-SNARK.
Tôi sẽ giải thích 1 cách dễ hiểu nhất như thế này:
Trước khi có thể dùng zk-SNARK cho bất kỳ vấn đề tính toán nào, ta phải chuyển đổi vấn đề đó thành một “dạng” phù hợp. Dạng này được gọi là QAP, hay “chương trình số học bậc hai“.
Một khi ta đã chuyển bài toán của mình thành QAP, ta sẽ tiến hành giải nó với một số đầu vào cụ thể. Giải pháp tìm được được gọi là “witness”. Điều này giống như khi ta giải xong câu đố và biết câu trả lời.
Bây giờ khi đã có câu trả lời, ta cần tạo ra một cách để chứng minh ta biết câu trả lời mà không tiết lộ nó. Quá trình này tạo ra một “bằng chứng không tiết lộ thông tin”, nghĩa là nó cho phép ta chứng minh rằng ta biết câu trả lời mà không cần phải nói ra nó.
Cuối cùng, người khác có thể sử dụng một quá trình riêng để kiểm tra bằng chứng ta đã tạo ra, để xác nhận rằng ta thực sự biết câu trả lời mà không biết câu trả lời thực sự là gì!
Ví dụ: Ta có phương trình như sau:
x**3 + x + 5 == 37 (gợi ý đáp án là 3)
Ta sẽ chứng minh ta biết nghiệm của phương trình toán học trên mà không cần phải tiết lộ nghiệm đó bằng cách viết 1 chương trình máy tính đơn giản như sau:

Chức năng hàm qevel sẽ tính toán giá trị của phương trình x**3 + x + 5. Khi ta thay số 3 vào x, hàm sẽ trả về 35, là kết quả ta mong muốn.
Tuy nhiên, ta sẽ thấy hạn chế của ngôn ngữ lập trình trong trường hợp này. Ngôn ngữ này chỉ hỗ trợ các phép toán số học cơ bản(+, -, *, /) và lũy thừa với số mũ cố định(x**7 chứ không phải x**y). Nó không hỗ trợ phép toán chia có dư (%) hoặc so sánh (>, <, ≤, ≥), vì không có cách nào hiệu quả để thực hiện modulo hoặc so sánh trực tiếp trong số học nhóm tuần hoàn hữu hạn.
Giải pháp ở đây là ta có thể mở rộng ngôn ngữ này để hỗ trợ thêm các phép toán như chia có dư và so sánh
Ví dụ:
if x < 5: y = 7; else: y = 9
bằng cách bằng cách chuyển đổi chúng sang dạng số học:
y = 7 * (x < 5) + 9 * (x >= 5)
Bạn có thể tham khảo một trình biên dịch có thể sử dụng để chuyển đổi mã lệnh thành dạng có thể dùng cho zk-SNARK được triển khai bởi vbuterin (chỉ dành cho mục đích giáo dục; chưa sẵn sàng để tạo QAP cho zk-SNARK trong thực tế)
Flattening
Bước đầu tiên để chuyển đổi sang dạng QAP này là bước “flattening”(làm phẳng), nói một cách dễ hiểu thì đây là bước biến đổi mã lập trình để nó trở nên đơn giản hơn, mỗi dòng chỉ thực hiện một hành động cơ bản.
Trong ví dụ trên, chương trình máy tính ban đầu có một biểu thức toán học phức tạp. Quá trình “flattening” tách biểu thức này ra thành các phần nhỏ, mỗi phần chỉ làm một phép tính đơn giản:
sym_1 = x * x
Nhân x với chính nó để tạo ra một giá trị trung gian, gọi là sym_1
y = sym_1 * x
Sau đó nhân giá trị trung gian sym_1 với x một lần nữa để tạo ra y, theo đúng phép tính x^3
sym_2 = y + x
Cộng y vừa tính được với x
~out = sym_2 + 5
Cuối cùng, cộng thêm 5 vào sym_2 để có kết quả cuối cùng và đặt dấu ~ trước out có thể để chỉ rằng đây là kết quả cuối cùng của chương trình.
Vô cùng dễ hiểu! Quá trình “flattening” này giúp chuẩn bị mã để có thể xử lý bằng zk-SNARK, vì zk-SNARK đòi hỏi mã lập trình phải ở dạng đơn giản để dễ dàng chuyển đổi thành các dạng toán học mà nó có thể làm việc được.
Gates to R1CS
Tiếp theo, chúng ta sẽ thực hiện 1 loạt các phép tính để chuyển đổi chúng thành một dạng phức tạp hơn một chút, gọi là (rank-1 constraint system) hệ thống ràng buộc cấp một, viết tắt là R1CS.
R1CS là một chuỗi gồm các nhóm gồm ba vectơ (a, b, c) và giải pháp cho R1CS là một vectơ s, trong đó s phải thỏa mãn phương trình:
s . a * s . b – s . c = 0
Điều này kiểm tra xem giá trị đầu ra có đúng là sản phẩm của hai giá trị đầu vào hay không. Nếu tất cả điều kiện này đều được thoả mãn, chúng ta có một vectơ giải pháp chính xác cho hệ thống.
Ta có thể xem hình ảnh dưới đây để hiểu rõ về R1CS hơn:
Trước hết, chúng ta sẽ định nghĩa các biến được sử dụng trong hệ thống, tôi sẽ cung cấp bước ánh xạ các biến như sau:
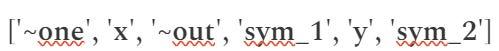
- “~one” (chỉ số đầu tiên biểu thị số 1)
- “x” (biến đầu vào)
- “~out” (biến đầu ra)
- “sym_1”, “y”, “sym_2” (các biến trung gian)
Vector “s” sẽ chứa giá trị cho tất cả các biến này, theo đúng thứ tự đã định nghĩa.
#Chúng ta sẽ đưa ra (a, b, c) cho bộ ba cho cổng đầu tiên (đối với phép nhân x * x):

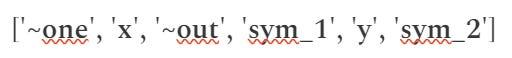
- Vectơ a và b cùng chứa giá trị [0, 1, 0, 0, 0, 0] . Số 1 ở vị trí thứ hai trong mỗi vectơ này biểu thị rằng giá trị của biến x sẽ được sử dụng trong tính toán. Cụ thể, giá trị này được nhân với chính nó vì cả a và b đều đặt trọng số tại vị trí x
- Vectơ c có giá trị [0, 0, 0, 1, 0, 0] , với số 1 ở vị trí thứ tư, biểu thị rằng giá trị tính toán từ a và b sẽ được so sánh với biến sym_1 trong vectơ s
a = [0, 1, 0, 0, 0, 0] : chỉ định rằng biến “x” sẽ tham gia vào phép tính.
b = [0, 1, 0, 0, 0, 0] : lại chỉ định rằng “x” sẽ được nhân với chính nó.
c = [0, 0, 0, 1, 0, 0] : kết quả sẽ được lưu vào biến “sym_1”
Khi “x = 3”, phép tính sẽ là “3 * 3 = 9”, điều này thỏa mãn ràng buộc “sym_1 = x * x”
#Tiếp theo là cổng Thứ hai (đối với phép nhân sym_1 * x):

Tương tự,
a = [0, 0, 0, 1, 0, 0] : chỉ định “sym_1” (9 nếu “x = 3”)
b = [0, 1, 0, 0, 0, 0] : chỉ định “x” (3 nếu “x = 3”)
c = [0, 0, 0, 0, 1, 0] : kết quả sẽ được lưu vào “y”
Phép tính là “9 * 3 = 27”, điều này thỏa mãn ràng buộc
#Tiếp theo là cổng Thứ ba (đối với phép cộng x + y)

Tương tự,
a = [0, 1, 0, 0, 1, 0] : chỉ định “x” và “y”
b = [1, 0, 0, 0, 0, 0] : sử dụng giá trị “1” (đại diện cho “~one”) để phép cộng được thực hiện đúng.
c = [0, 0, 0, 0, 0, 1] : kết quả được lưu vào “sym_2”
Phép tính là “3 + 27 = 30”, điều này thỏa mãn ràng buộc “sym_2 = x + y”
#Cuối cùng là cổng Thứ tư (đối với phép cộng sym_2 + 5):

Tương tự,
a = [5, 0, 0, 0, 0, 1] : sử dụng giá trị “5” từ “~one” và giá trị “1” từ “sym_2”
b = [1, 0, 0, 0, 0, 0] : lại là “~one” để phép cộng được thực hiện đúng.
c = [0, 0, 1, 0, 0, 0] : kết quả được lưu vào “~out”
Phép tính là “30 + (5*1) = 35”, điều này thỏa mãn ràng buộc “~out = sym_2 + 5”
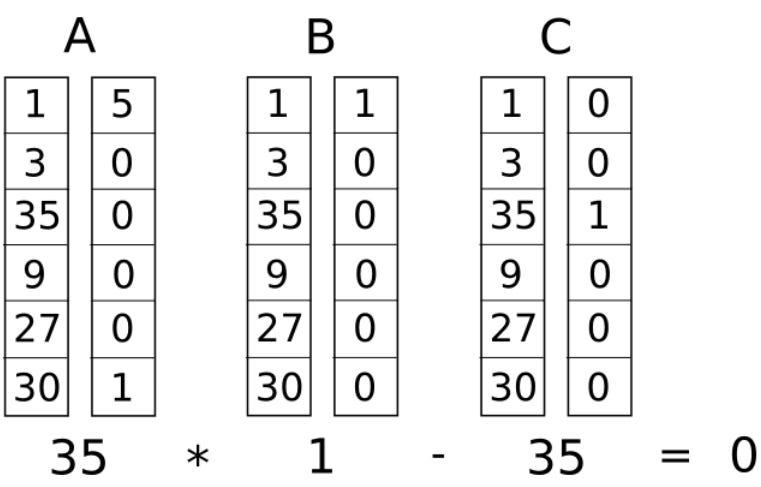
Ba cột A, B, và C tương ứng với các vector “a”, “b”, và “c”. Số “35” ở dưới cùng của cột C là kết quả cuối cùng (“~out”)
So sánh (s . a) * (s . b) và (s . c), chúng phải bằng nhau (hiệu của chúng phải bằng 0)
Lúc này, véc tơ “s” sẽ chứa các giá trị sau:
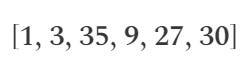
- 1: Đây là giá trị cho biến giả ~one, luôn là 1 để đại diện cho hằng số 1.
- 3: Đây là giá trị cho biến đầu vào x.
- 35: Đây là giá trị mong muốn, kết quả cuối cùng của chương trình (biến ~out).
- 9: Kết quả của x * x, được lưu trong sym_1.
- 27: Kết quả của sym_1 * x, được lưu trong y.
- 30: Kết quả của y + x, được lưu trong sym_2.
Cuối cùng, R1CS hoàn chỉnh được ghép lại với nhau như hình dưới đây:

R1CS to QAP
Bước tiếp theo là lấy R1CS này và chuyển đổi nó thành dạng QAP, nhưng thay vì dùng các vectơ và tích số chấm như trong R1CS

QAP sử dụng “đa thức” vì chúng có tính chất toán học đặc biệt giúp quá trình kiểm tra dễ dàng hơn.
Phép nội suy Lagrange(Lagrange interpolation) là phương pháp để vẽ một đường cong (đa thức) đi qua một loạt các điểm đã biết. Nếu bạn có một số điểm cụ thể và bạn muốn một đường cong (đa thức) chạm vào tất cả các điểm đó, phép nội suy Lagrange sẽ giúp bạn tìm ra đường cong đó.
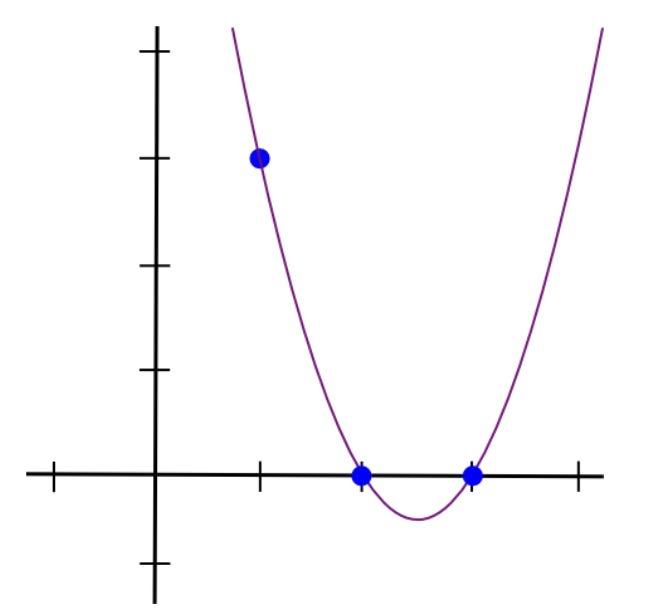
Ví dụ: Giả sử chúng ta muốn một đa thức đi qua (1, 3), (2, 2) và (3, 4). Chúng ta bắt đầu bằng cách tạo một đa thức đi qua (1, 3), (2, 0) và (3, 0).
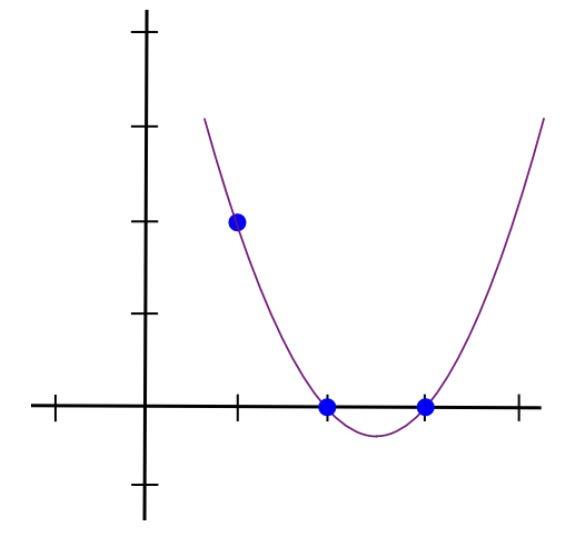
Một cách đơn giản để làm điều này là lấy tích của (x-2) và (x-3). Hàm số này sẽ có dạng uốn lượn, nhô lên tại x=1 và cắt trục hoành tại x=2 và x=3.
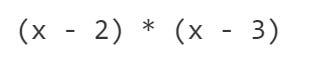
như bên dưới:
Bây giờ, chúng ta chỉ cần “điều chỉnh” nó sao cho chiều cao tại x=1 là đúng:
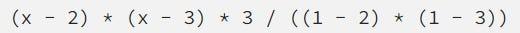
Điều này làm cho đa thức và đồ thị sẽ hiển thị như bên dưới:

Sau đó, chúng ta làm tương tự với hai điểm còn lại và nhận được hai đa thức khác, cộng cả ba lại với nhau và nhận được:


Thuật toán ban đầu mất thời gian O(n^3) để tính toán vì mỗi điểm trong n điểm cần O(n^2) để nhân các đa thức. Tuy nhiên, bằng cách suy nghĩ thông minh hơn, ta có thể giảm thời gian này xuống còn O(n^2).
Áp dụng các thuật toán như biến đổi FFT, ta có thể giảm thời gian tính toán nhanh hơn nữa, điều này rất quan trọng trong các ứng dụng như zk-SNARK với hàng nghìn cổng.
Chúng ta sẽ áp dụng phép nội suy Lagrange để biến đổi R1CS, bằng cách lấy giá trị đầu tiên của mỗi vector a, sau đó dùng phép nội suy này tạo đa thức cho từng vector, sao cho khi đánh giá đa thức tại một chỉ số cụ thể, ta nhận được giá trị đầu tiên của vector tương ứng.
Làm tương tự cho các giá trị đầu tiên của vector b và c, rồi áp dụng phương pháp này lần lượt cho các phần tử tiếp theo của mỗi vector.
Ta sẽ có kết quả như bên dưới:

Thuật toán sử dụng một dãy hệ số tăng dần để tạo ra đa thức:
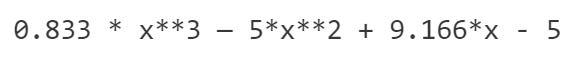
Đa thức này là thành phần của các tham số cho phiên bản QAP (Quadratic Arithmetic Program) đang xét.
Cần lưu ý là việc thiết lập các tham số này chỉ cần làm một lần cho mỗi hàm số được kiểm chứng bằng zk-SNARK; một khi đã thiết lập, chúng có thể tái sử dụng được.
Khi đánh giá tất cả các đa thức tại x=1, quá trình này rất đơn giản vì bạn chỉ việc cộng tất cả các hệ số (do 1^k luôn bằng 1 cho mọi giá trị của k).Ta sẽ có các kết quả sau:

- Đa thức A khi đánh giá tại x = 1 cho tất cả các kết quả là 0, trừ kết quả thứ hai là 1
- Đa thức B khi đánh giá tại x = 1 cũng cho tất cả các kết quả là 0, ngoại trừ kết quả thứ hai là 1.
- Đa thức C khi đánh giá tại x = 1 cho tất cả các kết quả là 0, ngoại trừ kết quả thứ tư là 1.
Ta thấy những gì chúng ta có ở đây giống hệt như bộ ba vectơ(a, b, c) cho cổng logic đầu tiên mà chúng ta đã tạo ở trên.
Nguồn bài viết: Team Tech/Research AlphaTrue
Nguồn tham khảo:
- Chen, T., Lu, H., Kunpittaya, T., & Luo, A. (2022). A review of zk-snarks. arXiv preprint arXiv:2202.06877. https://arxiv.org/pdf/2202.06877.pdf
- https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649
- https://eprint.iacr.org/2012/215.pd