格拉姆斯特丹方程

07-17

本文为机器翻译

展示原文

格拉姆斯特丹方程

非常感谢@potuz对模型的反馈。也感谢@barnabe和@terence 。

概述

Glamsterdam 方程旨在指导在较短时隙时间的背景下，选择延迟执行还是ePBS 。基于一组基本假设，计算两种时隙流水线配置的最大执行 gas/秒和 blob/秒。然后，根据用户在扩展性、时隙时间、简单性和无需信任性之间的优先级，计算出一个效用最大化的时隙配置。Glamsterdam 方程应被视为一种工具。它本身无法在辩论中给出明确的答案，原因有二：

一些建模决策可能会使结果偏向任一方向。为了生成易于概览的方程式，我们进行了某些简化。常数的选择是基于合理的推测，调整后可能会产生不同的结果。
我们对效用方程中较为主观的常数持有不同的看法。诸如去信任化交易所的价值或简洁设计等主观特质并未被量化，用户只需在U_O U O中提供其主观量化值即可。他们还可以通过效用弹性来指定不同扩展组件的重要性。

整体 Glamsterdam 效用函数指定为

U = (G^*_s)^{U_G} \乘以 (B^*_s)^{U_B} \乘以 (1/S^*)^{U_S} \乘以 U_O，

U = （ G ∗ s ） UG × （ B ∗ s ） UB × （ 1 / S ∗ ） US × UO ，

依赖于Fusaka在gas/s（ G^*_s， G ∗ s ）和blobs/s（ B^*_s， B ∗ s ）上的比例缩放，以及时隙时间S^* S ∗的相对减少。指数是效用弹性（默认值为1），指定了不同缩放组件的重要性。本文将首先分析推导延迟执行和ePBS在不同时隙时间（遵循简化假设）下可实现的缩放，然后返回效用函数。然后改变常数以分析不同假设和优化下的结果。最后，探索替代设计。

常量

以假设的 Fusaka 基线为起点，首先在以下常数下分析时隙流水线方程：

象征	价值	解释
L_G L G	0.8秒	全局延迟。最小区块充分传播以形成共识所需的时间。
L_D L D	0.8秒/MB	数据延迟。每 MB 数据完整传播所需的额外时间。
L_{RF} L R F	0.2秒	中继延迟。修复了将信标块发送到中继时的延迟问题。
L_{RD} L R D	0.15秒/MB	中继数据延迟。将信标块发送到中继时，每 MB 数据所需的额外时间。
b_b b b	1 MB	信标区块大小。必须容纳的信标区块的最大大小。
P_{bg} P b g	每 60M gas 消耗 1MB	每种 Gas 的有效载荷字节数。每种 Gas 的有效载荷的最大数据大小。
E_s E s	60M gas/s	执行速度。每秒可执行的最大 gas 量。
B_r B r	15 个 blob/秒	斑点速率。每秒可传播的最大斑点数量（源自 48 个斑点/ 4-L_G4 - L G秒）。
\bar{S } ¯S	12秒	基线槽长度。Fusaka基线槽长度。
\bar{G } _s¯G s	5M gas/s	基线最大 gas 吞吐量。效用函数中用作参考点的基线最大 gas/s（60M gas/12 秒）。
\bar{ B } _s¯Bs	4 个斑点/秒	基线 blob 吞吐量。效用函数中用作参考点的基线 blob/s（48 blob/12 秒）。
A_a A a	3秒	证明聚合时间。完整证明聚合所需的时间。
\mathrm{PTC}_d P T C d	1.4秒	Blob PTC 延迟。PTC投票在时隙结束时传播所需的裕度。
A_d A d	0.4秒	构建器延迟。构建器在最坏情况下，在认证截止日期之后等待的时间，之后才会在 ePBS 中发布有效载荷。

总中继延迟定义为L_R=L_{RF} + b_\text{b}L_{RD} L R = L R F + b b L R D ，其中整个帖子都使用L_R L R ，而不是写出各个组件。

常数是根据先前的分析和当前发展做出的有根据的猜测，例如： 1、2、3、4、5、6、7、8、9 。不确定性较高的常数的影响有时可能会被平均化，从而产生更切合实际的结果。例如，数据延迟L_D L D可能略显保守，而每gas 的有效载荷字节数P_{bg} P b g则较为激进，这假设数据成本会进一步调整。为了帮助读者形成个人观点，请参考以下公式：

运行分析和绘制图表的源代码将在网上发布（本周末），
结论部分探讨了基线设置的变化。

值得强调的一个具体简化分析是，在点对点层，blob 和区块传播之间的交互没有建模，而信标区块和有效载荷传播之间的交互则进行了建模。每个时隙的 blob 数量仅根据 Fusaka 规范中规定的可用传播时间（取决于时隙结构）得出，其中包括与区块相同的全局延迟L_G L G。这使得分析更加易于处理。考虑到各种验证者角色以及 CL/EL 交互，blob 如何与区块交互仍然是一个悬而未决的问题。

延迟执行

延迟执行采用简单配置，没有特殊的头部截止时间，并且 blob 必须在证明时可用。分析的目标是设置证明截止时间A A以最大化效用，该效用是 gas 和 blob 吞吐量的函数。一个 slot 中可包含的总 gas G G受执行时间和传播时间的限制。有效载荷传播的固定时间约束可以表示为

c = L_R + L_G + b_\text{b}L_D，

c = LR + LG + bbLD ，

包括中继延迟、全局延迟以及信标块的传播（消耗固定带宽，且无法同时用于有效载荷）。给定 gas 量G时，最大有效载荷大小为P_{bg}G P b g G字节，其中P_{bg} P b g是每单位 gas 的最大有效载荷大小。传播此有效载荷的时间取决于可用窗口Ac A − c ，从而得出以下约束：

G \le \frac{Ac}{P_{bg} L_D}。

G≤A − cPbgLD 。

Gas 还受到执行窗口SA S − A和执行速度E_s E s (gas/s) 的限制，从而给出第二个约束：

G \le E_s(SA)。

G≤Es （ S - A ）。

当G G的两个限制相等时，可以找到最大化潜在 gas 吞吐量的截止时间A_G A G ：

E_s(S-A_G) = \frac{A_G-c}{P_{bg} L_D}。

E s （ S − A G ） = A G − c P b g L D 。

求解A_G A G得出：

A_G = \frac{c + E_s P_{bg} L_D S}{1 + E_s P_{bg} L_D}。

A G = c + E S P b g L D S 1 + E S P b g L D 。

然而，总体目标是最大化效用，其中也包括 blob 吞吐量。将一个 slot 中的 blob 总数定义为B。效用函数的缩放项分别定义为 gas/s 和 blob/s 相对于当前基线（以条形突出显示）的变化：

G_s^* = \frac{G/S}{\bar{G}_s}, \;\;\;\;\;\; B_s^* = \frac{B/S}{\bar{B}_s}。

G ∗ s = G / S¯Gs ， B ∗ s = B / S¯ B s 。

效用最大化截止日期A_U A U是通过最大化整体效用函数的缩放项的乘积来找到的：

U_2 = (G^*_s)^{U_G} \times (B^*_s)^{U_B}。

U2 = （ G ∗ s ） UG × （ B ∗ s ） UB 。

一个有用的假设是，所寻求的最优解是执行受限的（即G \propto SA G ∝ S − A ），因为较晚的截止时间总是能提高 blob 的吞吐量。为了找到这个最优解，对数效用\ln U_2 ln对U 2进行分析。忽略不影响A A导数的常数项，该函数简化为：

\ln U_2 = \text{const} + U_G \ln(SA) + U_B \ln(A - L_G - L_R)。

在…中U 2 = const + U G ln （ S − A ） + UBln （ A − LG − LR ）。

对A A取导数可得：

\frac{d}{dA}(\ln U_2) = -\frac{U_G}{SA} + \frac{U_B}{A-L_G-L_R}。

d d A （对数U 2 ) = − U G S − A + U B A − LG − LR 。

将导数设为零并求解A A可得出最终表达式：

A_U = \frac{U_B S + U_G (L_G+L_R)}{U_G + U_B}。

AU = UBS + UG （ LG + LR ） UG + UB 。

然后，通过选择这两个候选者中的较晚者来选择最终的最佳截止期限A^* A ∗ ，该期限受允许进行证明聚合的最新可接受截止期限的限制， A_L = S - A_a A L = S − A a ：

A^* = \min(\max(A_G, A_U), A_L)。

A * = min ( max ( AG , AU ) , AL ) 。

一旦选定了最终期限A^* A ∗ ，则在该期限内可实现的总绝对气体G G可以通过取两个限值中的最小值来计算：

G = \min\left(E_s(SA^*)，\frac{A^*-c}{P_{bg} \cdot L_D}\right)。

G = min （ Es （ S - A ∗ ）， A ∗ -cPbg⋅LD ）。

由此得出最终的吞吐量。每秒的Gas为：

G_s = G/S，

Gs = G / S ，

每秒的 blob 数量由截止期限A^* A ∗和 blob 传播速率B_r B r决定，为：

B_s = \frac{(A^*-L_G-L_R) \cdot B_r}{S}。

Bs = （ A ∗ −LG − LR ） ⋅BrS 。

图 1 显示了最佳证明截止期限，该期限可以是：

有效载荷传播时间和执行时间之间的完美平衡（ A_G A G ；洋红色），
当忽略有效载荷传播时间的限制时，效用达到最优（ A_U A U ；红色），
在允许证明聚合的最新点（ A_L A L ；紫色）。

图 1

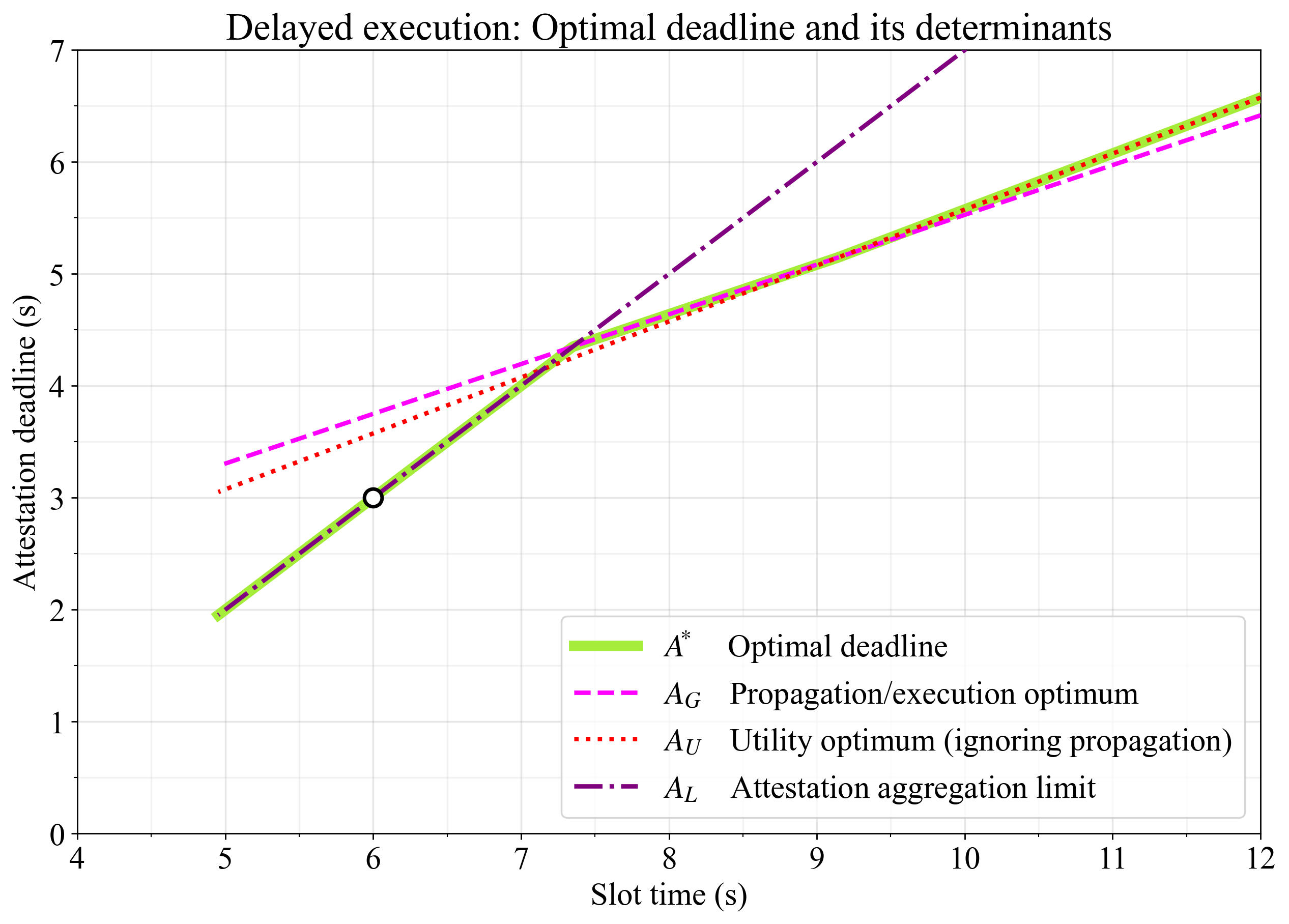
图 1.延迟执行中的最佳截止时间，即传播/执行 gas 最优值A_G A G ，纯执行受限模型中效用最大值A_U A U ，以及允许进行证明聚合的最新点A_L A L 。圆圈表示在 6 秒的时隙中，3 秒的证明截止时间的潜在目标。为了实现最佳吞吐量，这需要进行一些优化以缩短传播时间（将优化线向下推）。

使用默认常量，当时隙长度为 12 秒时，最佳截止时间约为 6.5 秒（ A_U A U机制）。在时隙时间低于 9 秒左右时，有效载荷传播时间会限制 Blob 和执行的效用最优值，因此必须通过选择更晚的证明截止时间（ A_G A G机制）来做出妥协。当时隙时间低于 7.3 秒左右时，在A_G A G下将不再有足够的时间进行证明聚合，并且必须通过选择更早的截止时间（ A_L A L机制）来牺牲吞吐量（传播）。在 6 秒时隙时间下延迟执行的实现可能会将目标锁定在 3 秒的证明截止时间（正如已经提出的）。为了在 6 秒时实现高吞吐量，必须通过以下优化来加快传播速度（下推图 1 中的优化线）：

使得通话数据更加昂贵，
改进 p2p 层，
实施多维费用市场或宏观定价（以限制最坏情况的有效载荷大小）。

还可以假设构建者自己可以选择有效载荷组合，以平衡任何给定截止期限的传播和执行，从而为早期截止期限留出余地。然而，对于字节数较大的有效载荷，这会给有效载荷传播带来压力。即使遵守 Gas Limit，此类有效载荷也可能无法被接受。这也是多维费用市场如此有吸引力的原因之一。

电子PBS

在对 ePBS 进行建模时，使用双截止期限方法，允许最佳有效载荷 PTC 截止期限\mathrm{PTC}_P P T C P，同时将 PTC DA 截止期限保持在时隙的最晚可能点

\mathrm{PTC}_B=S-\mathrm{PTC}_d。

PTCB = S − PTCd 。

有效载荷在无需信任的环境中发布，在最坏的情况下，构建者必须在证明截止日期之后发布有效载荷A_d A d 。附录 A 中讨论了将A_d A d纳入分析的相关性。blob 的发布时间设置为c c ，这样构建者就无需等待A_d A d完成证明计数后再发布，从而允许稍长一些的传播时间。ePBS 中的证明截止日期设置得比延迟执行中的早，具体为常数c c ：

A = c = L_G + b_b L_D。

A = c = LG + b b L D。

然后，有效载荷在c+A_d c + A d处释放，并在传播时继承其自身的全局延迟L_G L G 。剩下的唯一任务是计算有效载荷的最佳 PTC 截止时间\mathrm{PTC}_P P T C P ，该截止时间严格定义为使总 gas 值G G最大化的点。

gas 的数量受执行窗口S-\mathrm{PTC}_P S − P T C P和执行速度E_s E s (gas/s) 的限制：

G \le E_s(S-\mathrm{PTC}_P)。

G≤Es （ S - PTCP ）。

它还受到传播有效载荷所需时间的限制。一笔包含 Gas G的有效载荷最多需要L_G + (G \cdot P_{bg} \cdot L_D) L G + ( G ⋅ P b g ⋅ L D )才能传播，并且必须允许其最迟在\mathrm{PTC}_P P T C P截止时间到达：

c + A_d + L_G + (G \cdot P_{bg} \cdot L_D) \le \mathrm{PTC}_P。

c + A d + LG + ( G ⋅ P b g ⋅ L D ) ≤ P T C P 。

这给出了传播过程中的气体约束：

G \le \frac{\mathrm{PTC}_P - c - A_d - L_G}{P_{bg}L_D}。

G≤PTCP - c - Ad - LGPbgLD 。

当G G的两个限制相等时，可以找到最佳截止日期\mathrm{PTC}^*_P P T C ∗ P ：

E_s(S-\mathrm{PTC}_P) = \frac{\mathrm{PTC}_P - c - A_d - L_G}{P_{bg}L_D}。

E s （ S - P T C P ） = P T C P - c - A d - L G P b g L D 。

对\mathrm{PTC}_P P T C P求解并通过\mathrm{PTC}_B P T C B进行钳位可得出最终方程：

\mathrm{PTC}^*_P = \min\Bigg(\mathrm{PTC}_B, \;\frac{c + A_d + L_G + E_s P_{bg} L_D S}{1 + E_s P_{bg} L_D}\Bigg)。

P T C ∗ P =最小值( P T C B , c + A d + LG + E s P b g L DS 1 + E s P b g L D ）。

一旦找到最佳截止时间\mathrm{PTC}^*_P P T C ∗ P ，就可以确定最终的吞吐量。每秒 gas 消耗量G_s G s由传播约束得出：

G_s = \frac{\mathrm{PTC}_P - c - A_d - L_G}{P_{bg}L_DS}。

Gs = P T C P − c − A d − LG Pbg L D S 。

每秒的 blob 数量B_s B s由 blob 传播的可用时间（从其在c c处发布到 blob 截止时间\mathrm{PTC}_B P T C B ，同时考虑其自身的全局延迟 $L_G$）和 blob 速率B_r B r决定：

B_s = \frac{(\mathrm{PTC}_B - c - L_G) \cdot B_r}{S}。

Bs = （ PTCB - c - LG ） ⋅BrS 。

图 2 显示了在基线常数下最大化 ePBS 吞吐量的最佳截止时间。

图 2

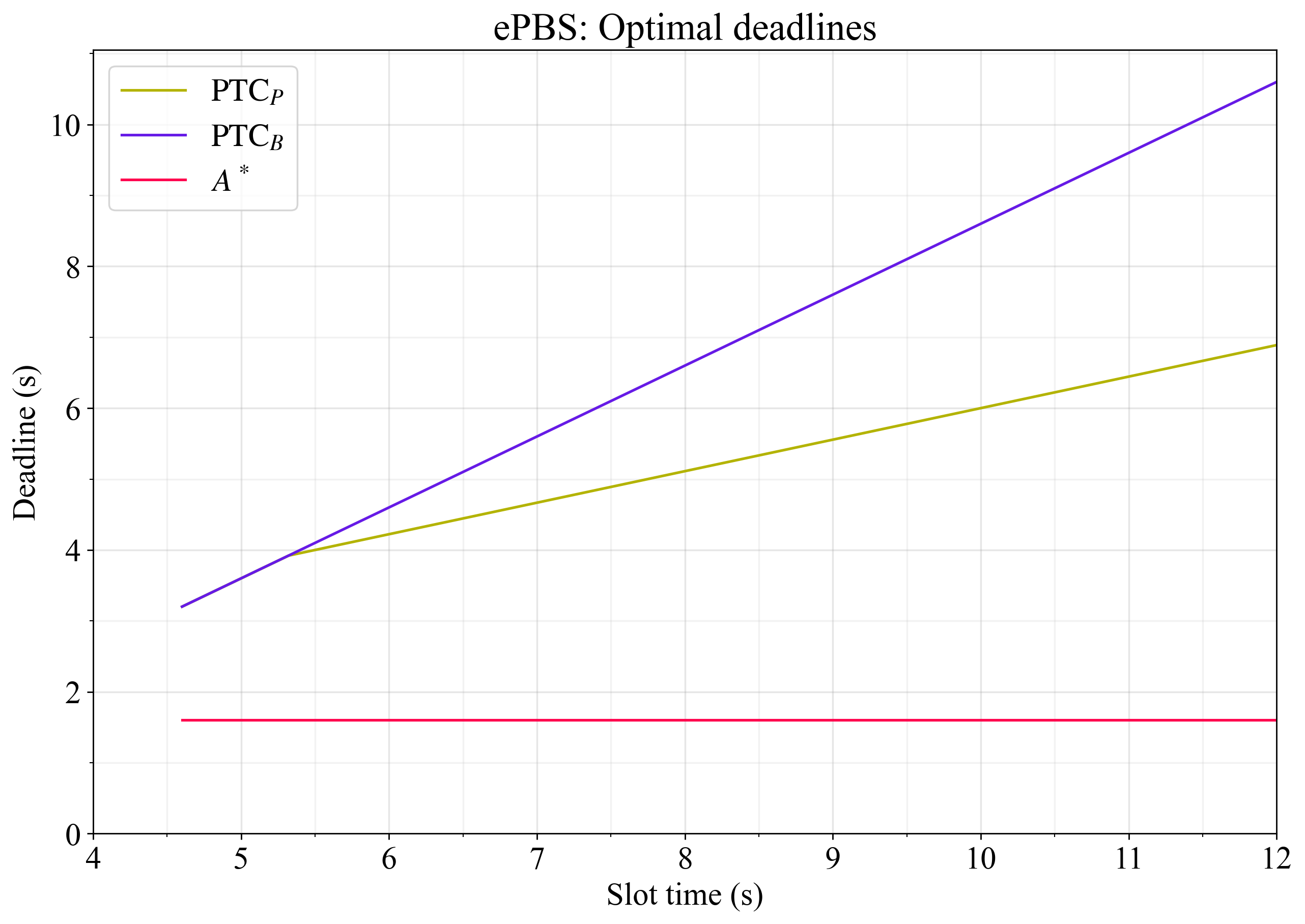
图 2.在基线常数下，最大化 ePBS 吞吐量的最佳截止时间。有效载荷观测截止时间\mathrm{PTC}^*_P P T C ∗ P设定在传播和执行之间达到完美平衡的点，并遵循 PTC 在\mathrm{PTC}_B P T C B投票后无法发生的限制。

延迟执行和 ePBS 的吞吐量

图 3 展示了延迟执行和 ePBS 的执行速率（Mgas/s 和 blobs/s）。显然，ePBS 特别适合扩展 blobs，因为它提供了较晚的 PTC 截止时间。由于有效载荷的截止时间可以独立设置，因此吞吐量会随着时隙时间的缩短而平滑衰减，直到传播时间最终被限制在 5.5 秒以下。吞吐量的平滑下降是由于以下因素的相对重要性不断增加：

全局延迟L_G L G ，
信标块传播时间c c ，
构建者确定信标区块将收集足够的证明A_d A d所需的时间，
以及 PTC 投票传播时间\mathrm{PTC}_d P T C d 。

延迟执行最适合在较长的时隙时间范围内扩展 L1 gas 的使用，因为在时隙开始时产生的延迟会减少L_G-L_R+A_d L G − L R + A d ，并且使用默认常量，可以在传播和执行之间合理地平衡证明截止时间。当证明聚合约束在 7.3 秒左右生效时，吞吐量曲线会出现一个拐点。由于在基准常量下传播时间不足，吞吐量会大幅低于此时隙长度。

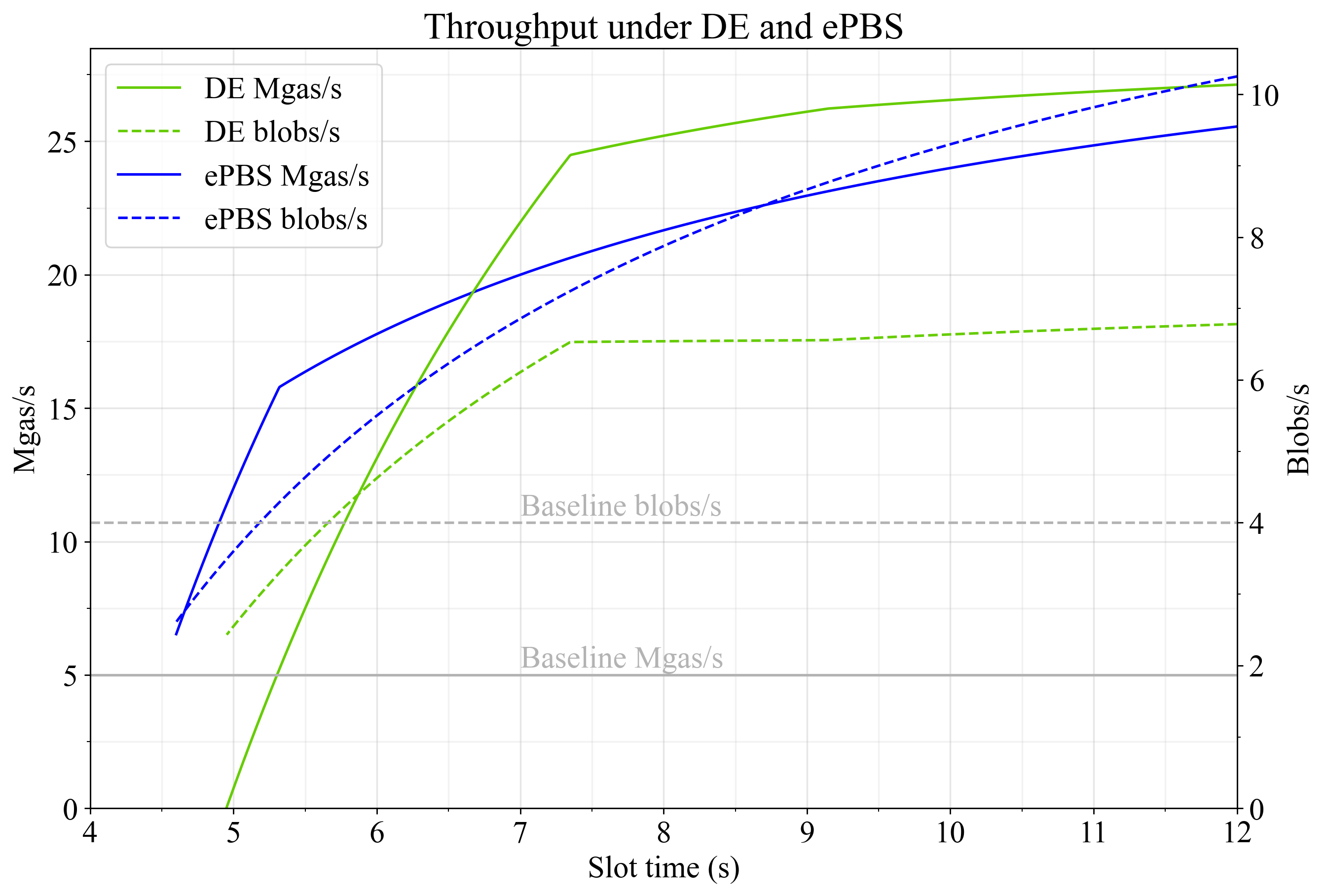
图 3.不同时隙下延迟执行（绿色）和 ePBS（蓝色）下的吞吐量，分别以 Mgas/s（实线）和 blobs/s（虚线）表示。即使在较短的时隙时间内，这两种方法都有可能显著扩展以太坊。

根据 Glamsterdam 方程的效用

Glamsterdam 方程捕捉了时隙重构带来的扩展性，它考虑了时隙时间的相对变化S^* S ∗以及一个主观缩放因子U_O U O，该因子可以反映任何其他因素。如果优先考虑不改变分叉选择和不设置 PTC 的简单性，则有人可能会将U_O>1 U O > 1赋给 DE。另一方面，例如，如果构建者和提议者之间的去信任支付被视为关键，则有人可能会将U_O>1 U O > 1赋给 ePBS。完整的方程式如下：

U = (G^*_s)^{U_G} \乘以 (B^*_s)^{U_B} \乘以 (1/S^*)^{U_S} \乘以 U_O。

U = （ G ∗ s ） UG × （ B ∗ s ） UB × （ 1 / S ∗ ） US × UO 。

该方程还包含效用弹性，用于指定效用度量中不同绩效指标的重要性。效用弹性为 1 表示效用与指标成正比，而弹性为 0 表示指标与整体效用无关。这些弹性包括：

U_G U G – 执行吞吐量的效用弹性。
U_B U B – blob 吞吐量的效用弹性。
U_S U S – 较短时隙时间的效用弹性。

图 4 展示了延迟执行和 ePBS 的效用在时隙时间的变化情况，使用了U_G=1 U G = 1 、 U_B=1 U B = 1 、 U_S=1 U S = 1和U_O=1 U O = 1 的设置。两种重组方案带来的效用增益大致相同，其中延迟执行在 7.3 秒时隙时间达到峰值，而 ePBS 在 10 秒时隙时间左右达到峰值。

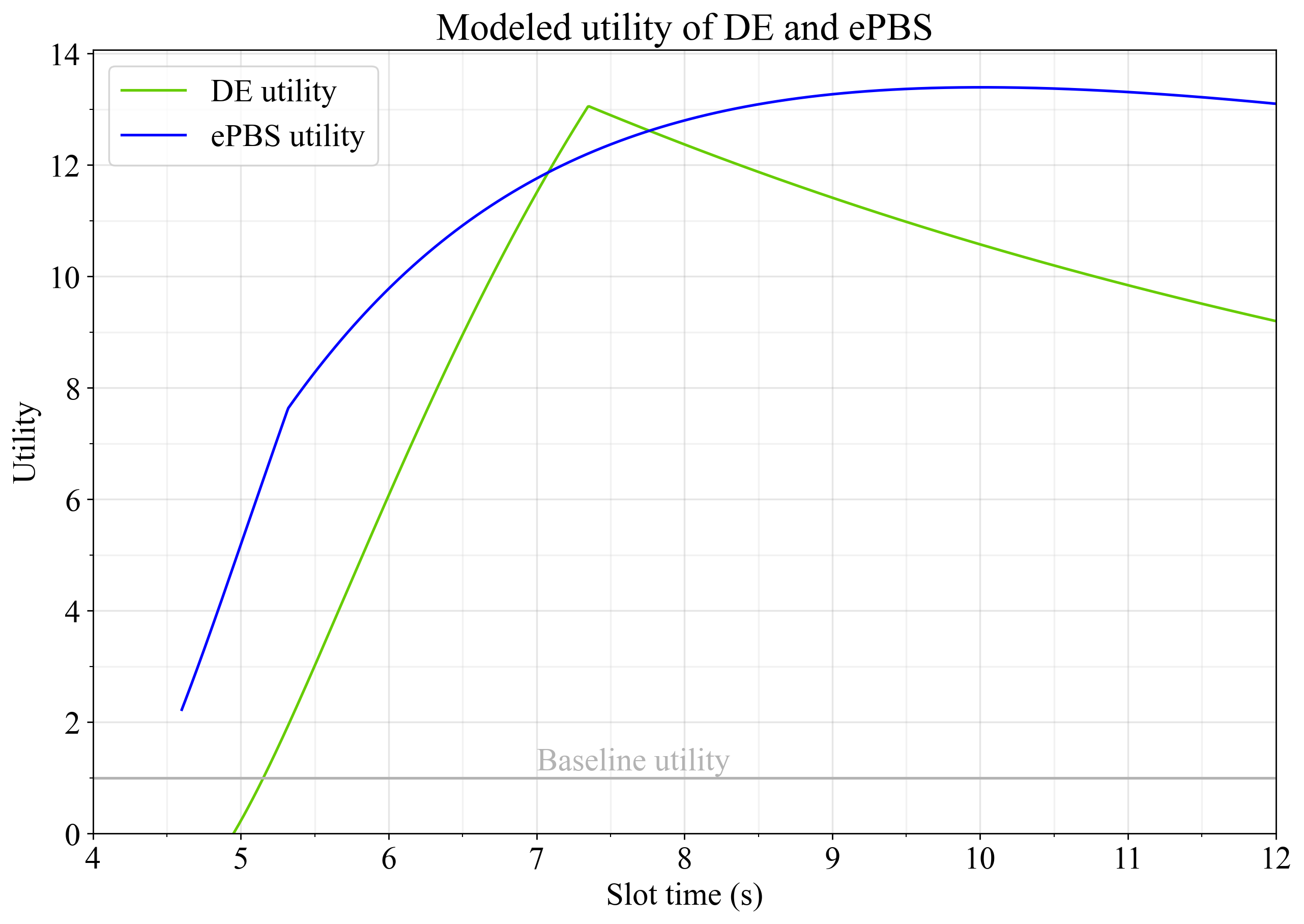
图 4.当所有弹性都设置为 1 且U_O=1 时，延迟执行和 ePBS 的效用，两个选项的U O = 1 。

我们对哪些指标最重要有着不同的看法，因此弹性指标也至关重要。例如，考虑到Fusaka计划中每时隙32个blob的目标已经是一个显著的改进，而目前6个blob的目标实际上并未消耗，因此将blob的进一步扩展的重要性赋予低于执行气体扩展的重要性似乎是合理的。U_G =1 U G = 1和U_B=0.4 U B = 0.4的弹性指标体现了这一概念。缩短时隙时间的重要性可能介于两者之间，例如U_S=0.7 U S = 0.7 。

图 5 展示了这些弹性条件下的结果，由于 blob 扩展的重要性被赋予得较低，延迟执行在某种程度上更受青睐。另一方面，一些人可能认为 ePBS 本质上更优，因为它能够促进构建者和提议者之间无需信任的合作。设置 ePBS 的U_O=1.1， U_O = 1.1体现了 ePBS 在不可衡量的品质方面比延迟执行好 10% 的概念。蓝色虚线体现了这一点，并且当 ePBS 的时隙时间约为 9 秒时，或当 DE 的时隙时间约为 7.3 秒时，其效用达到最大化。

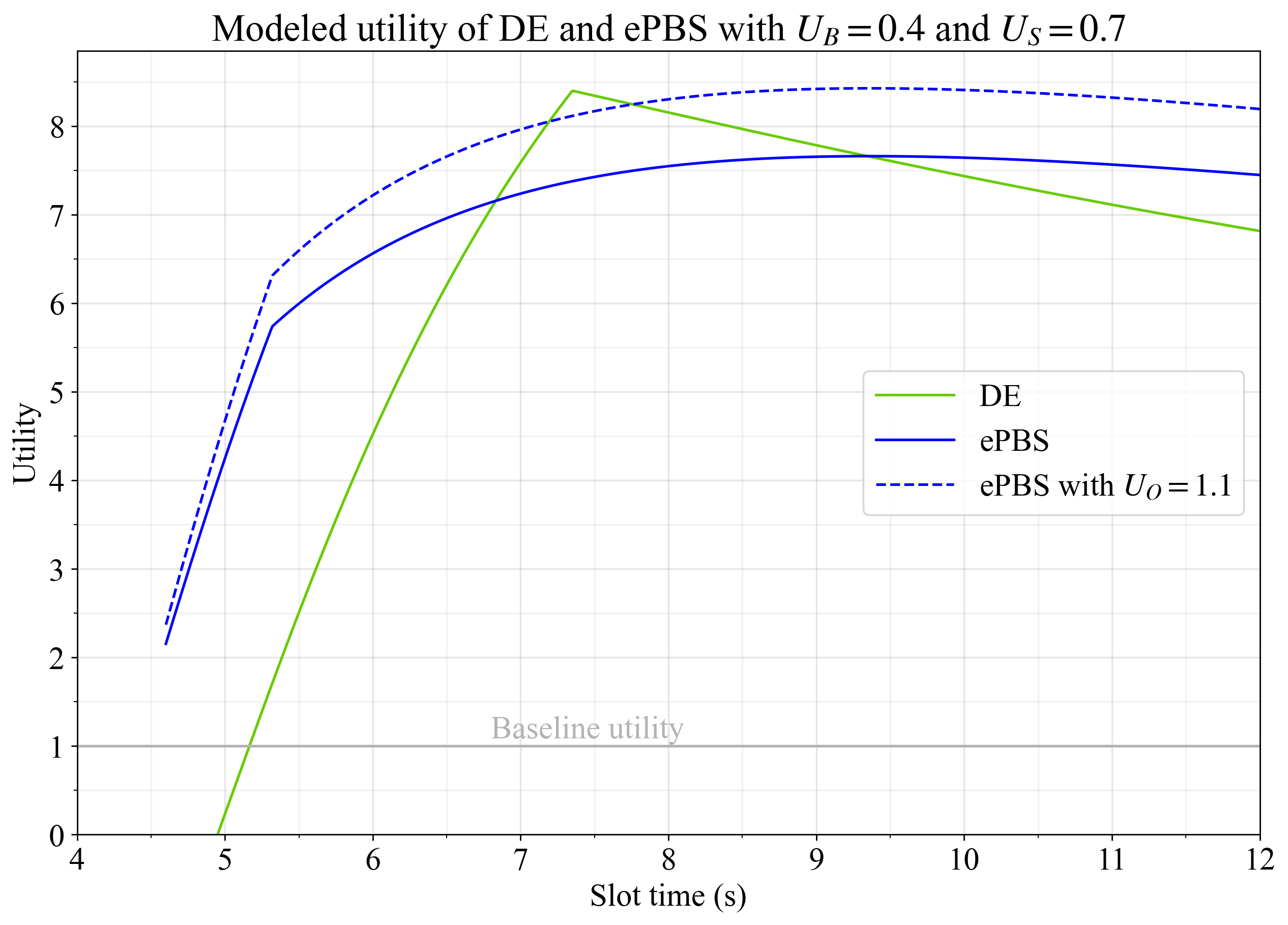
图 5.延迟执行和 ePBS 的效用，弹性系数为U_G=1， U G = 1 ， U_B=0.4 U B

来源

免责声明：以上内容仅为作者观点，不代表Followin的任何立场，不构成与Followin相关的任何投资建议。

喜欢