感谢Shao 、 Chih Cheng Liang和Panta Rhei的反馈和讨论。
抽象的
以太坊正进入大规模网络容量扩容时期。随着Fusaka分叉中PeerDAS的推出,blob容量将按计划扩容至48/72。然而,由于blob需求增长跟不上供应容量,导致供应过剩,导致blob费用市场在较长时间内无法有效运作。
本提案引入了双变量资源定价机制,作为 EIP-1559 的扩展,该机制会根据实际需求波动动态调整每base_fee_per_blob_gas和每区块target_blob_gas_per_block 。这种方法可以稳定区块费用,并确保区块费用市场在整个网络扩展阶段保持有效。
动机
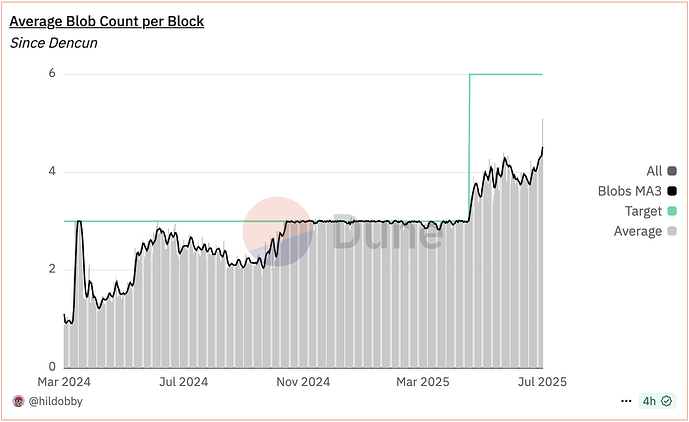
目前,以太坊上的资源费用会随着网络拥堵程度而波动,拥堵期间费用上涨,使用率低时费用下降。在有效市场中,资源稀缺性会驱动价格与供需相匹配。然而,当我们通过增加资源目标和限额来扩展网络容量时,资源的稀缺性会导致供应过剩。由于需求没有相应地上升到新的目标水平,价格不再反映市场均衡,变得无效。过去一年,我们已经看到了 blob 使用中这种不平衡的迹象:
- 大多数情况下,Blob 使用量低于目标值。实际上,需求不会立即响应供应变化。Blob 需求逐渐增长,达到目标消耗水平仍需时日。在此之前,
base_fee_per_blob_gas几乎保持免费。
- 当需求接近目标水平时,每blob gas
base_fee_per_blob_gas会变得非常不稳定。由于价格起始价格仅为1wei,即使blob gas使用量的微小波动也可能导致价格剧烈波动。这种波动尤其明显,因为市场由少数主要消费者主导,他们的高blob gas使用量往往集中在同一时期,这进一步放大了价格波动并降低了可预测性。
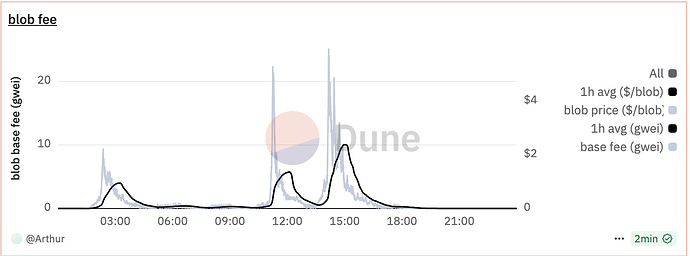
下图展示了 2025 年 5 月 5 日(Pectra 分叉之前)基础费用的波动情况。数据显示价格出现了三次飙升,但在大部分时间段内,费用几乎保持免费。
- 每次我们提高
target_blob_gas_per_block规模,base_fee_per_blob_gas就会再次下降到 1 wei。这意味着我们会反复遇到问题 (1) 和 (2)。当PeerDAS和BRO上线时,我们预计base_fee_per_blob_gas会在相当长的一段时间内保持为零。
双变量 EIP-1559 机制
当前 blob 基础费用计算如下:
b_{n+1}=b_n∗exp(\frac{g_i−T}{8T}) b n + 1 = b n ∗ e x p ( g i − T 8 T )
其中b_n b n是当前区块的基本费用, b_{n+1} b n + 1是下一个区块的基本费用, g_i g i是当前使用的 gas, T T是目标 blob gas,固定为 6。有关更多详细信息,请参阅此处。
我们建议将目标 blob gas 设置为变量,以动态调整基础费用( b_i b i )和目标费用( t_i t i )。此机制有以下用途:
- 调节目标周围的 blob gas 使用量,这代表网络可以长期轻松处理的持续容量。
- 基本费用仍作为基于网络拥堵情况的底价。
- 当网络扩展 blob 容量时稳定基本费用。
基本费用调整
调整基础费用的目的是围绕 Gas 目标值来调节 Gas 消耗量。与原版 EIP-1559 类似,调整规则根据上一个区块的基础费用( b_ {i-1} b i − 1 ) 、 Gas 目标值(t_{i-1} t i − 1)和已用 Gas( g_{i-1} g i − 1 ) ,使用以下公式计算当前区块的基础费用( b_i b i )。其中, K_b表示每单位过剩 Gas 的调整率:
b_{i+1} = b_i \, (1 + K_b \times (g_i - t_i)) b i + 1 = b i ( 1 + Kb × ( g i − t i ) )
我们可以将此方程转换为指数形式(有关完整推导,请参阅Dankrad Feist 的帖子):
b_n = b_0 \, \exp(K_b \sum_{i=0}^{n-1} g_i - t_i) b n = b 0经验值( K b ∑ n − 1 i = 0 g i − t i )
即使目标是一个变量而不是固定数字,公式仍然与原始公式相同。根据定义, K_b = \frac{1}{\text{基础费用更新分数}} K b = 1基础费用更新分数且\sum_{i=0}^{n-1} g_i - t_i = \text{Excess Blob Gas} ∑ n − 1 i = 0 g i − t i = Excess Blob Gas 。因此,我们不需要更改任何现有的实现。
基本费用敏感度
每单位过剩 blob gas 的调整率 ( K_b K b ) 提供了一种便捷的方法来考虑基础费用的敏感性。在EIP-7691中,新的 2:3 的目标与最大比率破坏了 blob 满用和空用场景之间对称的响应性。这种不对称导致base_fee_per_blob_gas在 blob 满用的情况下增加约 8.2%,而在空用的情况下减少约 14.5%。
我们不再关注对满载和空载 blob 使用情况的响应是否对称,而是将对称响应重新定义为,无论过量 gas 是增加还是减少,都对等量的过量 gas 变化应用相同的百分比调整。这种方法可确保在动态目标条件下,基础费用敏感度保持一致。
我们建议恢复12.5%作为基础费用的最大变化率,并使用以下公式计算K_bK b :
\exp(K_b \times \max(abs(g_i - t_i))) \approx 1.125 exp ( K b × max ( a b s ( g i − t i ) ) ) ≈1.125
目标调整
调整目标的目的是为了缓解基础费用的波动性( \Delta b = b_{i+1} - b_i Δ b = b i + 1 − b i )。由于目标代表了持续容量的动态范围,因此当需求落在此范围内时,目标会进行调整以维持稳定的费用,从而确保网络能够处理不同的使用模式,而不会出现过度的波动。
当前块的目标可以使用以下等式计算,其中K_t K t表示每单位的调整率:
t_{i+1} = t_i(1 + K_t \times (\Delta b - 0)) t i + 1 = t i ( 1 + K t × ( Δ b − 0 ) )
将此方程转换为指数形式:
t_n = t_0 \exp(K_t \sum_{i=0}^{n-1} \Delta b) = t_0 \exp(K_t \times (b_n - b_0)) t n = t 0 exp ( Kt∑n − 1i = 0Δb ) = t0exp ( Kt × ( bn − b0 ) )
目标变量具有如下定义的约束:
t_i \in [t_{min}, t_{max}] t i ∈ [ t m i n , t m a x ]
为了方便起见,我们可以将参考基础费用定义为MIN_TARGET_BLOBS_PER_BLOCK和MAX_TARGET_BLOBS_PER_BLOCK 。每单位价格变动的调整率 ( K_t = \frac{1}{\text{Target Blob Update Fraction}} K t = 1 Target Blob Update Fraction )可以使用以下公式计算:
K_t = \dfrac{\ln{\dfrac{t_\text{max}}{t_\text{min}}}}{b_\text{最大目标} - b_\text{最小目标}} K t = ln最大时间最小时间 b最大目标− b最小目标
数学模型
双变量 EIP-1559 机制中的具体调整规则仅使用以下公式计算基础费用和目标费用:
b_n = b_0 \, \exp(K_b \sum_{i=0}^{n-1} g_i - t_i) b n = b 0经验值( K b ∑ n − 1 i = 0 g i − t i )
t_n = t_0 \exp(K_t \times (b_n - b_0)) t n = t 0 exp ( Kt × ( bn − b0 ) )
该模型的关键点是:
- 每当使用的 blob gas 大于或小于目标 blob gas 时,基本费用就会分别向上或向下移动。
- 目标不是一个固定的数字,而是根据当前的基本费用动态变化的。
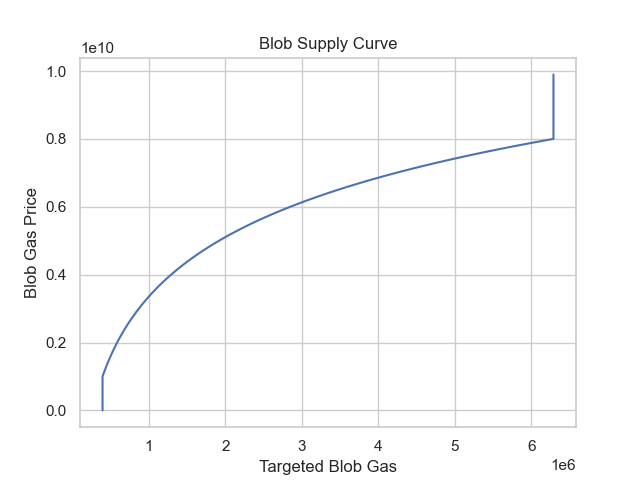
下图展示了具有供应弹性的供应曲线,其中产能对当前价格做出动态反应,而不是维持固定目标。
参数
该提案中引入的新参数包括:
-
MIN_TARGET_BLOBS_PER_BLOCK -
MAX_TARGET_BLOBS_PER_BLOCK -
MIN_TARGET_BLOB_GAS_PER_BLOCK -
MAX_TARGET_BLOB_GAS_PER_BLOCK -
BASE_FEE_AT_MIN_TARGET_BLOBS -
BASE_FEE_AT_MAX_TARGET_BLOBS -
TARGET_BLOB_UPDATE_FRACTION
仿真分析
为了进行以下模拟分析,这些参数设置如下:
MIN_TARGET_BLOBS_PER_BLOCK = 3 MAX_TARGET_BLOBS_PER_BLOCK = 48 MAX_BLOBS_PER_BLOCK = 72 BASE_FEE_AT_MIN_TARGET_BLOBS = 1_000_000_000 BASE_FEE_AT_MAX_TARGET_BLOBS = 8_000_000_000 GAS_PER_BLOB = 2 ** 17 MIN_TARGET_BLOB_GAS_PER_BLOCK = MIN_TARGET_BLOBS_PER_BLOCK * GAS_PER_BLOBMAX_TARGET_BLOB_GAS_PER_BLOCK = MAX_TARGET_BLOBS_PER_BLOCK * GAS_PER_BLOBMAX_BLOB_GAS_PER_BLOCK = MAX_BLOBS_PER_BLOCK * GAS_PER_BLOBMAX_EXCESS_BLOB_GAS_PER_BLOCK = max (MAX_BLOB_GAS_PER_BLOCK - MIN_TARGET_BLOB_GAS_PER_BLOCK,MAX_BLOB_GAS_PER_BLOCK - MAX_TARGET_BLOB_GAS_PER_BLOCK,MIN_TARGET_BLOB_GAS_PER_BLOCK - 0 ,MAX_TARGET_BLOBS_PER_BLOCK - 0 , 0 )BLOB_BASE_FEE_UPDATE_FRACTION = int (MAX_EXCESS_BLOB_GAS_PER_BLOCK / np.log( 1.125 ))TARGET_BLOB_UPDATE_FRACTION = int ((BASE_FEE_AT_MAX_TARGET_BLOBS - BASE_FEE_AT_MIN_TARGET_BLOBS) / np.log(MAX_TARGET_BLOBS_PER_BLOCK / MIN_TARGET_BLOBS_PER_BLOCK)) 场景 1:Blob 需求低于最低目标
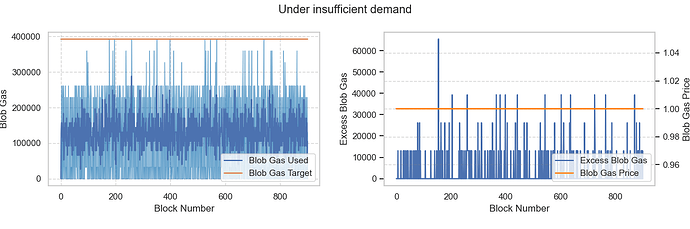
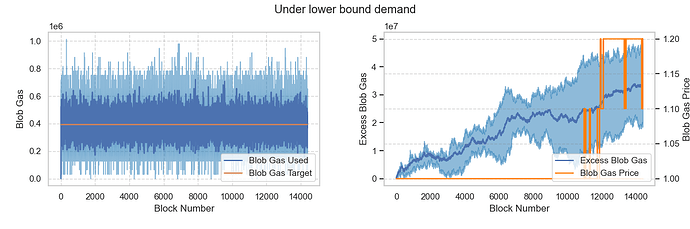
假设平均需求约为 2 个 blob,低于MIN_TARGET_BLOBS_PER_BLOCK ,即供应过剩的情况。结果显示,基本费用仍保持在MIN_BASE_FEE_PER_BLOB_GAS wei,符合预期。
场景 2:Blob 需求接近最低目标
假设平均需求量约为 3 个 blob,相当于MIN_TARGET_BLOBS_PER_BLOCK 。结果显示,过剩的 blob gas 开始累积,基础费用上升至MIN_BASE_FEE_PER_BLOB_GAS以上。
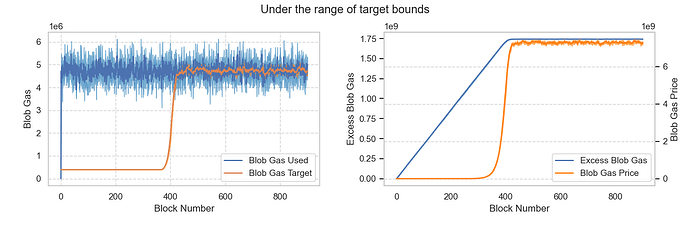
场景 3:Blob 需求介于最小目标和最大目标之间
假设平均需求约为 36 个区块,介于MIN_TARGET_BLOBS_PER_BLOCK和MAX_TARGET_BLOBS_PER_BLOCK之间。结果显示,目标区块大约需要 400 个区块来调整并跟踪实际需求。当市场达到均衡时,基础费用保持稳定。
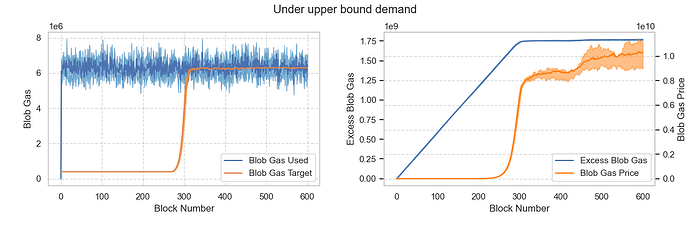
场景 4:Blob 需求接近最大目标
假设平均需求量约为 48 个区块,相当于MAX_TARGET_BLOBS_PER_BLOCK 。结果显示,目标区块需要大约 300 个区块才能达到MAX_TARGET_BLOBS_PER_BLOCK数量。此后,基础费用将由 EIP-1559 的原始价格更新函数控制。
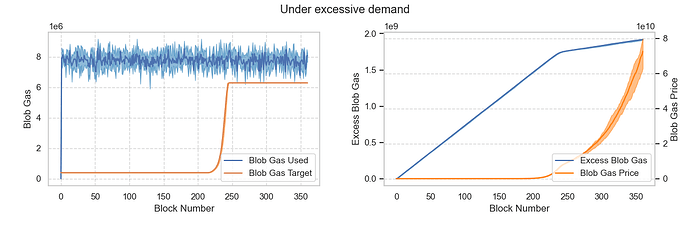
场景 5:Blob 需求高于最大目标
假设平均需求量约为 60 个区块,超过了MAX_TARGET_BLOBS_PER_BLOCK上限。结果显示,目标区块需要 240 个区块才能达到MAX_TARGET_BLOBS_PER_BLOCK上限。此后,基础费用将如预期般呈指数级增长。
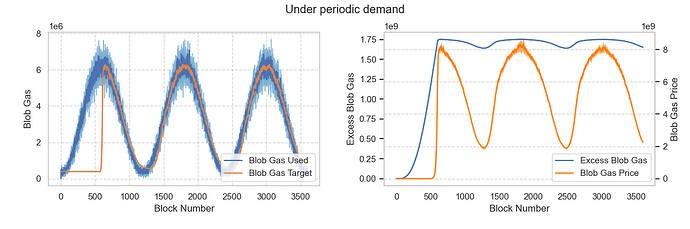
场景 6:Blob 需求定期变化
假设平均需求在[3, 48]范围内呈周期性变化。结果表明,实际需求上升时,目标blob增加;实际需求下降时,目标blob减少。基础费用也随实际需求不断变化。
费用市场增长生命周期
根据以上结果,我们确定了双变量 EIP-1559 费用市场的三个阶段:
初期阶段:实际需求小于或等于MIN_TARGET_BLOBS_PER_BLOCK 。市场缺乏有效的价格信号来合理匹配供需;无论实际使用模式如何,价格始终保持在最低水平。但是,我们可以通过设置相对较低的MIN_TARGET_BLOBS_PER_BLOCK和BASE_FEE_AT_MIN_TARGET_BLOBS值来轻松引导市场。
增长阶段:实际需求介于MIN_TARGET_BLOBS_PER_BLOCK和MAX_TARGET_BLOBS_PER_BLOCK之间。目标 Blob 和基础费用均受机制控制,并随着实际需求稳步变化。随着 Blob 供应量的扩大,市场不会回到初始阶段。
成熟阶段:实际需求超过MAX_TARGET_BLOBS_PER_BLOCK 。目标 Blob 达到MAX_TARGET_BLOBS_PER_BLOCK 。基本费用会根据网络拥堵情况波动。
实证分析
我们使用Blobscan API收集了从区块 22431084 到 22481502(代表 Pectra 分叉后一周)的区块数据。
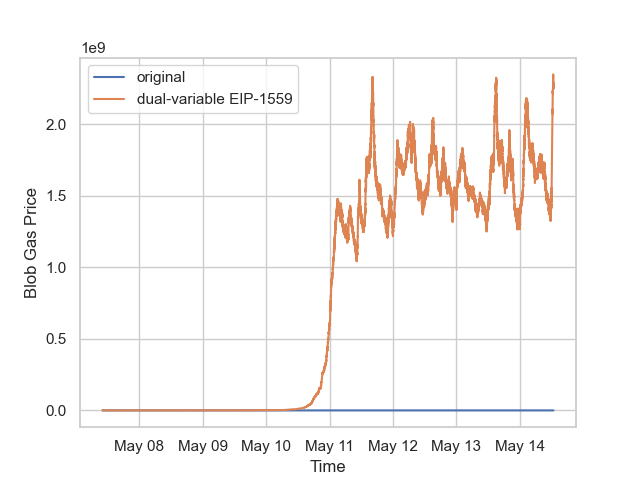
我们可以看到,由于 Blob Gas 使用量低于目标值,Pectra 分叉后 Blob Gas 价格(蓝线)迅速跌至 1 wei,表明供应过剩。此后,Blob Gas 价格一直保持在 1 wei, Dune Analytics 的数据也证实了这一点。
当我们使用相同的历史数据模拟双变量 EIP-1559 机制时,结果(橙色线)显示,blob gas 价格大约需要 4 天才能上涨到 1.5 gwei 左右,并且目标 blob 遵循现实世界的 blob 需求来平衡供需。
关于其他 EIP 的一些想法
Blob 容量扩展策略
当前,以太坊数据可用性 (DA) 层的扩展策略是使用仅修改 blob 参数 (BRO) 分叉,它提供了一种轻量级机制,可以通过仅修改 blob 相关参数( target和max )的硬分叉来逐步扩展 blob 容量。与传统硬分叉相比,BRO 分叉不仅降低了协调的复杂性和风险,还允许 Layer 2 利益相关者参与测试和推进升级。因此,它代表了一种相对高效的迭代扩展解决方案。
然而,这种解决方案也存在一些缺陷。首先,由于供应过剩,每次升级 Blob 容量时,基础费用仍然会降至 1 wei。这意味着我们必须反复从零开始增加需求。其次,BRO 分叉仍然是硬分叉,需要人工协调和决策,这会带来政治冲突和潜在的延迟。
与现有方法相比,双变量 EIP-1559 为扩展 Blob 容量提供了更有效的解决方案。它使以太坊能够实时响应 Blob 需求,并在扩展期间稳定 Blob 费用。整个流程无需许可且无需信任地运行。L1 客户端团队和 L2 利益相关者可以通过在此机制中设置适当的参数来专注于网络安全,而市场力量则决定供需之间的最佳平衡。
Gas 限制缩放
近期有消息称,以太坊计划将 gas 上限提高至每区块 4500 万,这将有可能提高 L1 网络效率和 L2 吞吐量。
区块 Gas 限制的扩展可能会面临与 Blob 扩展相同的供应过剩问题。为了避免这种供应过剩的情况,未来双变量 EIP-1559 也可以应用于区块 Gas 限制或任何多维资源。
关于 EIP-7918
EIP-7918建议将 blob 基础费用与实际执行 gas 成本挂钩,以确保 blob 交易对区块使用量做出相应贡献。
虽然双变量 EIP-1559 与 EIP-7918 并不冲突,但两者都试图解决与 Blob 费用市场有效性相关的类似问题。在我看来,双变量 EIP-1559 在多维 EIP-1559 路线图中提供了一个更清晰的解决方案。在 EIP-7918 下,将各种资源费用关联起来会使定价流程变得复杂。随着多维 EIP-1559 的推出,资源定价的复杂性将提升几个数量级,使费用更难预测。当 Blob 需求下降,而执行 Gas 价格却上涨时,用户可能会感到困惑。
结论
可以将其想象成一个智能高速公路收费系统。原始的 EIP-1559 仅在交通拥堵时调整收费价格。我们的双变量系统更加智能:它还可以根据长期交通模式添加或移除收费车道。当交通量持续超出容量时,它会逐步开放更多车道并调整价格。当交通量持续较低时,它会关闭部分车道以维持合理的收费价格。这使得该系统在增长和扩展阶段都具有经济可行性。
未来1-2年内,blob吞吐量将按计划扩展至48/72,当二维采样实现后,最大blob数量可能增加到512个。随着网络容量的扩展,我们也将解决当前定价系统所依赖的拥堵问题。预计在扩展期间,费用市场将失效。
双变量 EIP-1559 机制解决了网络扩容过程中费用市场崩溃的关键问题。通过实时自动调整价格和容量,该机制能够为验证者提供经济激励,为用户提供可预测的成本,并在整个扩容阶段确保网络安全。最重要的是,该解决方案易于实施,因为它在现有 EIP-1559 的基础上进行了少量改动。无论市场需求是快速增长还是下降,费用市场都能保持强劲有效。