认知状态:早期探索
最近,关于更积极地缩短以太坊插槽时间的讨论不断进行。这可以通过两种方式实现:
- 减少\deltaδ参数(我们对最大预期网络延迟的假设)。只有在p2p层获得降低延迟的改进时,才能安全地这样做
- 重新架构插槽结构,以减少一个插槽中的网络延迟轮次。
目前正在进行大量p2p强化和优化工作以实现(1);启用显著加速的最佳候选是擦除编码。研究工作正集中于(2)。
本文将论证(2)的最佳方法可能是稍微偏离在3SF中引入的插槽和最终性之间的紧密耦合,而是拥有一个更加分离的LMD GHOST分叉选择规则和最终性小工具,参与者数量不同。
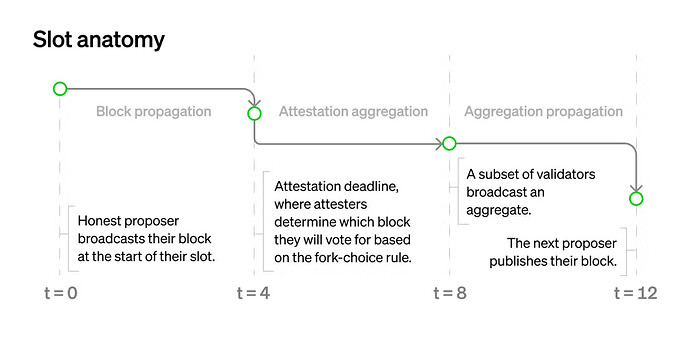
首先,让我们看看当前的插槽结构(来源):
这里的\deltaδ是4秒。第一部分(区块传播)是不可避免的。现在,请注意有两个与证明相关的阶段:聚合和传播。这是因为有太多证明(每个插槽约30,000个)无法直接传播。相反,我们首先在子网内广播一个子集,然后在全局p2p网络中广播聚合。
如果我们大幅增加验证者数量(例如,每个插槽100万个),我们可能需要增加到三个阶段以保持每个阶段的规模可管理(事实上,之前的写作正是这样建议的)。
总的来说,我们可以近似:
aggregation\_time = log_C(validator\_count)aggregation_time=logC(validator_count)
其中CC是容量:可以在单个子网中安全地同时广播多个签名。看起来C的实际值在数百到数千之间。如果我们希望具有量子抵抗性,应该假设更保守的数字(例如,如果量子抗性签名占用3 KB,并且每个插槽有256个,那么每个插槽将是768 kB,大致类似于最坏情况下的执行区块大小)。
最终性取决于"完整验证者集"的参与;如果我们(i)接受更多的权益质押中心化或强制委托,或者(ii)进行Orbit,可能是8192个,否则可能更多(很可能是10^5105到10^6106)。也就是说,要么是C^2C2,要么是C^3C3,取决于我们的假设。
同时,稳定的LMD GHOST实例只需要随机选择的法定人数参与;在这里,大小为256(即小于CC)就可以实现非常低的失败率。
这意味着,任何试图在每个插槽中完成一步最终性共识的方法,本质上将需要3C3C或4C4C(加上一个CC用于提议者)。同时,如果我们不这样做,一步将只需要2C2C。
这引导我提出以下关键建议:
- 建立一个LMD GHOST链,每个插槽随机选择约256个验证者。将其用作主要的"心跳"
- 有一个紧密跟随的最终性共识机制(实际上,在大约12C12C内最终确定),使用所有活跃验证者。不要尝试耦合LMD GHOST投票和最终性共识投票;将它们视为完全分离。
这给我们带来以下好处:
- 非常快的插槽时间,对于正常情况足够好,且不改变任何安全假设(因为"聚合"步骤不再是插槽时间的一部分)
- 我们可以自由选择最终性共识机制,包括使用现成的传统机制(例如Tendermint)
- 我们得到了"如何处理不活跃泄漏"的自然答案:在不活跃泄漏期间,LMD GHOST链继续,最终性共识停止。LMD GHOST链本身决定不活跃泄漏的进展,这决定了何时可以恢复最终性
- 我们可以为共识步骤做出更雄心勃勃的选择(例如,1个ETH验证者要求和100万个验证者)
- 更简单,因为交互效应更少,并且因为我们可以在不需要类似Orbit的技术的情况下获得更高的验证者数量