前言
在上一部分中,我们基本上了解了zk-SNARK 背后的数学和编码基础。现在我将继续深入研究更新且相当复杂的概念,以便您可以更深入地了解zk-SNARK背后的技术!
算术电路(算术电路)
运算电路的概念
该运算电路是一个有向无环图(DAG) ,或者简单地说,它是一个有向无环图,包括:
- 这些节点Vai加法门和乘法门。
- 边代表导体,建立在有限场Fp 上。一根电线将一个端口的输出连接到另一个端口的输入。每个端口有两个输入和一个输出。
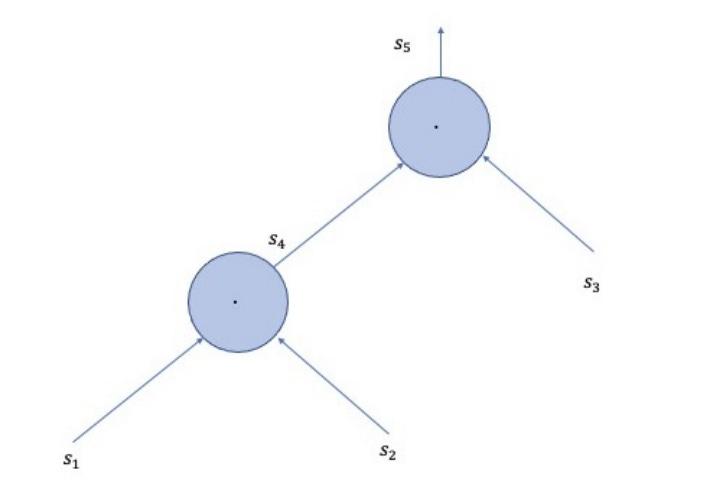
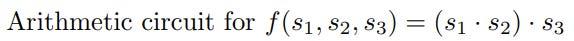
算术电路以最终输出结束。上图展示了一个算术电路的示例,我们可以看到数据如何被处理并通过每个门以制作最终结果。
算术电路告诉我们zk-SNARK如何处理和证明计算,而不透露任何信息。算术电路可以用图表来描述,其中包含系统排序的算术运算。
算术电路的运算
考虑上图,算术电路允许我们计算
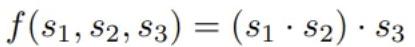
看上图,我们看到这个过程从第一个内核门开始,它接收s1和s2作为输入,并制作s4作为输出。接下来, s4和s3被输入到第二个内核门以制作最终输出s5 。
对于m端口、 n线电路,我们将能够确定
见证人 s = (s1, s2, s3,…, sn)
分配给电路的n条线,使得每个门的输入和输出满足由门的操作确定的约束。
一个m端口、 n线运算电路确定证人之间的关系
s = (s1, s2, …, sn)
这样对于一个常数

然后
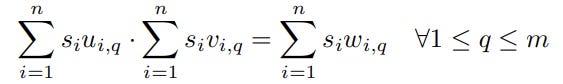
上述约束属于m个rank-1约束的集合,其目的是模拟算术电路中乘法门的输入和输出之间的关系。
特定的1 级约束的一个例子是 Eq
s1 。 s2 – s3 = 0。
该方程描述了电路中的乘法器门,它采用两个输入s1和s2 ,然后产生输出s3 。因此, s1和s2的乘积必须等于s3才能满足方程。
像这样的一组 m阶 1约束可以推广为二次算术程序。
QAP是将算术电路转换和下降为更容易验证操作而无需重新渲染整个电路的形式的工具。
二次算术程序
zk-SNARK的核心在于二次算术程序(QAP )。 QAP可以代表任何算术电路,包括加法门和乘法门。基于QAP,证明器可以制作他知道输入值,而无需透露有关该值或程序内部行为的任何信息。
zk-SNARK研究员Eran Tromer从基本数学原理出发,得出了zk-SNARK构建流程如下:

上面的步骤可以Chia两半。在本文中,将深入解释该过程的“前半部分” 。该过程的“前半部分”可以认为是从“计算”到“QAP”的步骤,这是将初始计算转换为可用于建立zk-SNARK 的数学形式的部分。
我将用最容易理解的方式解释如下:
在我们可以使用zk-SNARK解决任何计算问题之前,我们必须将问题转换为合适的“形式” 。这种形式称为QAP ,即“二次算术程序”。
一旦我们将问题转换为QAP ,我们将继续使用一些特定的输入来解决它。找到的解决方案称为“证词”。这就像我们解决完一个谜题并知道答案一样。
现在我们有了答案,我们需要制作一种方法来证明我们知道答案而不透露答案。这个过程制作了一个“非泄露证据”,这意味着它允许我们证明我们知道答案,而不必说出来。
最后,其他人可以使用单独的过程来检查我们制作的证据,以确认我们确实知道答案,而不知道答案实际上是什么!
例如:我们有以下等式:
x**3 + x + 5 == 37 (建议答案为 3)
我们将通过编写一个简单的计算机程序来证明我们知道上述数学方程的解,而不必揭示解,如下所示:

qevel函数将计算方程x**3 + x + 5的值。当我们将数字 3 代入 x 时,函数将返回 35,这就是我们想要的结果。
然而,在这种情况下我们会看到编程语言的局限性。该语言仅支持基本算术运算(+、-、*、/)和固定指数的幂(x**7,而不是 x**y) 。它不支持余Chia(%)或比较(>、<、≤、≥) ,因为在有限循环群算术中没有直接执行取模或比较的有效方法。
这里的解决方案是我们可以扩展该语言以支持其他操作,例如余数Chia和比较
例如:
如果 x < 5:y = 7;否则:y = 9
将它们转换为算术:
y = 7 * (x < 5) + 9 * (x >= 5)
您可以参考一个编译器,该编译器可用于将代码转换为vbuterin实现的zk-SNARK可用的形式(仅用于教育目的;尚未准备好在实践中为zk-SNARK创建QAP )
扁平化
转换为这种形式的QAP的第一步是“扁平化”步骤,简单来说,这是对编程代码进行改造以使其更简单的步骤,每行只执行一个基本操作。
在上面的示例中,初始计算机程序具有复杂的数学表达式。 “展平”的过程将这个表达式分成小部分,每个部分只做一个简单的计算:
sym_1 = x * x
将x与其自身相乘以制作一个中间值,称为sym_1
y = sym_1 * x
然后将中间值sym_1次乘以x以制作y ,遵循精确计算x^3
sym_2 = y + x
添加刚刚用x计算出的y
〜输出 = sym_2 + 5
最后将sym_2加 5 得到最终结果,并在out前加一个~表示这是程序的最终结果。
非常容易理解!这种“扁平化”过程有助于准备要由zk-SNARK处理的代码,因为zk-SNARK要求编程代码采用简单的形式,可以轻松转换为它可以使用的数学形式。
通往 R1CS 的大门
接下来,我们将进行一系列的计算,将它们转换成稍微复杂一点的形式,称为(rank-1约束系统) ,缩写为R1CS。
R1CS是由三个向量(a, b, c)组成的组的链, R1CS 的解是向量s,其中s必须满足以下方程:
s。作为 。 b – s 。 c = 0
这将检查输出值是否是两个输入值的正确乘积。如果满足所有这些条件,我们就有了系统的精确解向量。
我们可以看下图来更好地理解R1CS :
首先,我们将定义系统中使用的变量,我将提供映射变量的步骤如下:
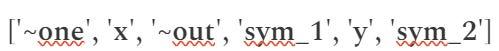
- “~one” (第一个下标代表数字1)
- “x” (输入变量)
- “~out” (输出变量)
- “sym_1”、“y”、“sym_2” (中间变量)
向量“s”将包含所有这些变量的值,按照定义的顺序。
#我们将给出第一个门的三元组(a,b,c) (对于x * x乘法):

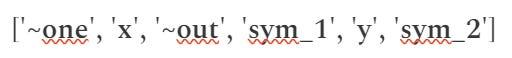
- 向量a和b都包含值[0, 1, 0, 0, 0, 0] 。每个向量中第二个位置的数字 1 表示将在计算中使用变量x的值。具体来说,该值与其自身相乘,因为a和b都将权重放在位置x处
- 向量c的值为[0, 0, 0, 1, 0, 0] ,第四位为数字 1,表示根据a和b计算出的值将与向量s中的变量sym_1进行比较
a = [0, 1, 0, 0, 0, 0] :指定变量“ x ”参与计算。
b = [0, 1, 0, 0, 0, 0] :再次指定“ x ”将与其自身相乘。
c = [0, 0, 0, 1, 0, 0] :结果将存储在变量“ sym_1 ”中
当“ x = 3 ”时,计算结果为“ 3 * 3 = 9” ,满足约束“sym_1 = x * x”
#接下来是第二个门(用于乘法sym_1 * x ):

相似的,
a = [0, 0, 0, 1, 0, 0] :指定“ sym_1 ”(如果“x = 3”则为 9 )
b = [0, 1, 0, 0, 0, 0] :指定“ x ”(如果“x = 3”则为 3 )
c = [0, 0, 0, 0, 1, 0] :结果将保存在“ y ”中
计算结果为“ 9 * 3 = 27 ”,满足约束条件
#接下来是第三个门(用于x + y 加法)

相似的,
a = [0, 1, 0, 0, 1, 0] :指定“x”和“y”
b = [1, 0, 0, 0, 0, 0] :使用值“1” (代表“~one” )以便正确执行加法。
c = [0, 0, 0, 0, 0, 1] : 结果保存到“sym_2”
计算结果为“3 + 27 = 30” ,满足约束“sym_2 = x + y”
#最后是第四个门(用于加法sym_2 + 5 ):

相似的,
a = [5, 0, 0, 0, 0, 1] :使用“~one”中的值“ 5 ”和“sym_2”中的值“ 1 ”
b = [1, 0, 0, 0, 0, 0] :再次“ ~one” ,以便正确执行加法。
c = [0, 0, 1, 0, 0, 0] : 结果保存到“ ~out”
计算结果为“30 + (5*1) = 35” ,满足约束条件“~out = sym_2 + 5”
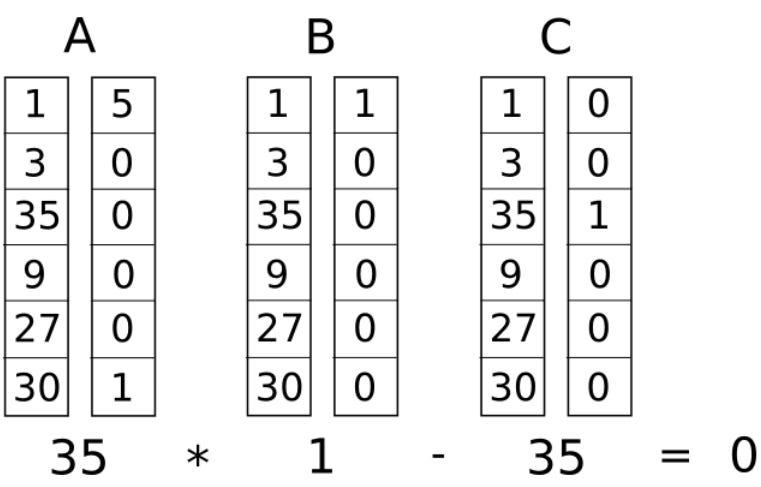
三列A、B和C对应于向量“ a” 、“ b”和“c ”。 C列底部的数字“ 35 ”是最终结果( “~out”)
比较(s . a) * (s . b)和(s . c),它们必须相等(它们的差必须为 0)
此时,向量“s”将包含以下值:
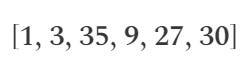
- 1:这是虚拟变量~one的值,它始终为 1 来表示常量 1。
- 3:这是输入变量x的值。
- 35:这是期望的值,程序的最终结果(变量~out) 。
- 9: x * x的结果,存储在sym_1中。
- 27: sym_1 * x的结果,存储在y中。
- 30: y + x的结果,存储在sym_2中。
最后,完整的R1CS拼凑起来如下图:

R1CS 至 QAP
下一步是采用此R1CS并将其转换为QAP 形式,但不是像R1CS那样使用向量和点积

QAP使用“多项式”,因为它们具有特殊的数学属性,可以使测试过程变得更容易。
拉格朗日插值是一种绘制经过一系列已知点的曲线(多项式)的方法。如果您有特定数量的点并且想要一条接触所有这些点的曲线(多项式) ,拉格朗日插值将帮助您找到该曲线。
例如:假设我们想要一个经过(1, 3)、(2, 2)和(3, 4) 的多项式。我们首先创建一个通过(1, 3)、(2, 0)和(3, 0) 的多项式。
一种简单的方法是取(x-2)和(x-3)的乘积。该函数将具有曲线形状,在 x=1 处上升并在x=2和x=3处切割水平轴。
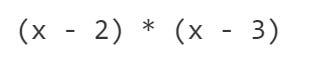
如下:
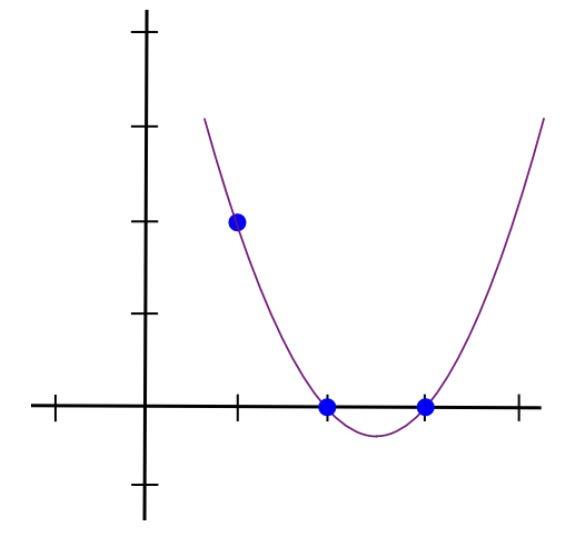
现在,我们只需要“调整”它,使x=1处的高度正确:
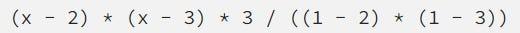
这使得多项式和图形将显示如下:

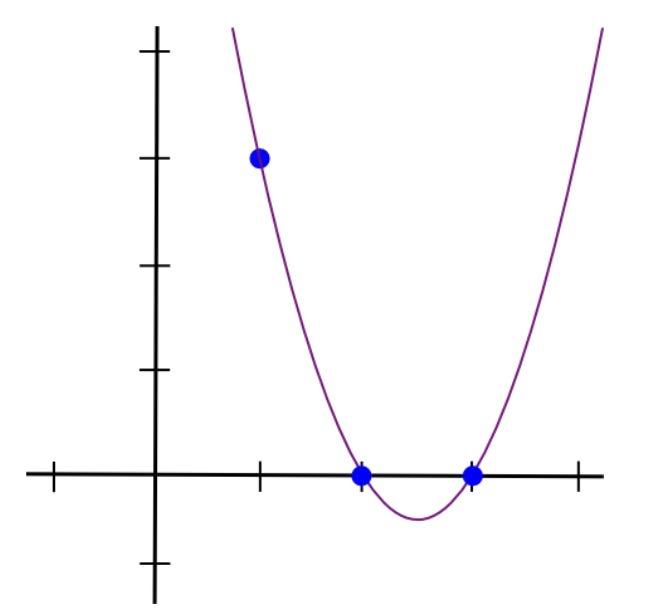
然后我们对剩下的两个点做同样的事情,得到另外两个多项式,将三个多项式加在一起得到:


原始算法需要O(n^3)时间来计算,因为每个n点都需要O(n^2)来乘以多项式。然而,通过更聪明的思考,我们可以将这个时间下降到O(n^2) 。
应用FFT变换等算法,我们可以更快地下降计算时间,这对于具有数千个门的zk-SNARK等应用非常重要。
我们将应用拉格朗日插值来变换R1CS ,方法是获取每个向量 a的第一个值,然后使用此插值为每个向量创建一个多项式,以便在索引特定数字处评估多项式时,我们得到第一个值对应的向量。
对向量b和c的第一个值执行相同的操作,然后次将此方法应用于每个向量的下一个元素。
我们将得到如下结果:

该算法使用一系列上涨系数来制作多项式:
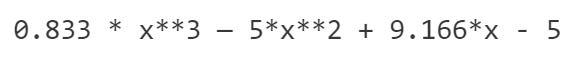
该多项式是正在考虑的QAP(二次算术程序)版本的参数的一部分。
需要注意的是,对于每个使用zk-SNARK验证的功能,这些参数只需要设置次;一旦设置完毕,它们就可以重复使用。
当评估x=1处的所有多项式时,过程非常简单,因为您只需将所有系数相加(因为对于k的所有值,1^k始终为1 ),我们将得到以下结果:

- 当多项式 A 在 x = 1评估时,除第二个结果为 1 外,所有结果均为 0
- 当在 x = 1评估多项式 B 时,除第二个结果为 1 外,所有结果也均为 0。
- 当多项式 C 在 x = 1评估时,所有结果均为 0,除了第四个结果为 1。
我们看到这里的向量三元组(a,b,c)与我们上面创建的第一个逻辑门完全相同。
文章来源: Team Tech/Research AlphaTrue
参考来源:
- 陈 T.、卢 H.、Kunpittaya, T. 和罗 A. (2022)。 zk-snarks 的评论。 arXiv 预印本 arXiv:2202.06877 。 https://arxiv.org/pdf/2202.06877.pdf
- https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649
- https://eprint.iacr.org/2012/215.pd








