在Vocdoni ，我們花了六年時間推進去中心化投票解決方案，專注於將 web2 應用程序與 web3 技術相結合。我們已成功為足球俱樂部、市議會、協會、政黨、專業機構、受起訴的運動等組織執行了高風險投票。

直到今天，我們一直依賴於定製的權威證明第 1 層網絡。
但我們認為，現在是時候過渡到基於零知識（zk）的基礎設施，以實現完全去中心化並解決數字投票系統的主要挑戰

在設計新協議提案的過程中，我們希望收到來自以太坊社區的反饋 。

通過借鑑我們的專業知識、MACI 和其他方面的想法。我們引入了一種新的通用投票協議，該協議解決了諸如無收據、選民隱私、審查透明度、通用審計以及消除對可信協調員的需求等關鍵問題。

該系統專為可擴展性和可訪問性而設計，可實現適合大規模採用的高頻低成本投票。我們利用 zkSNARK 和閾值同態加密 (ElGamal)，確保終端用戶的端到端可驗證性和匿名性。

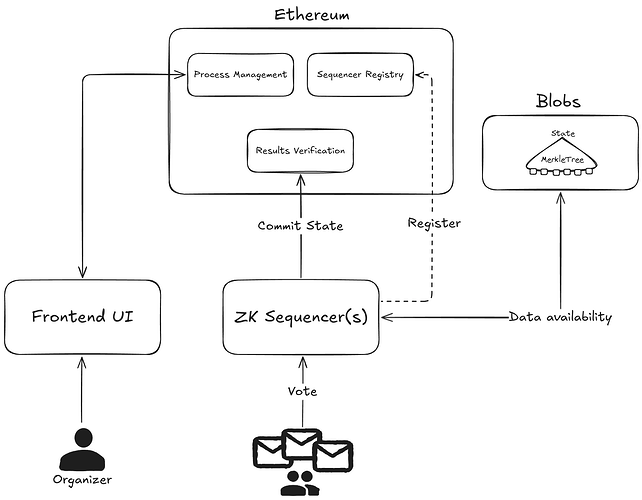
基於 zkSNARK 的去中心化狀態機作為以太坊區塊鏈上的專用第 2 層運行，提供抗審查性、完整性、無需信任的操作和透明的結果審查。通過智能合約協調的排序器之間的分佈式密鑰生成 (DKG) 允許在不依賴中央機構的情況下創建安全且去中心化的加密密鑰。

大多數組件都已使用可訪問的技術實現，並經過了概念驗證測試，確認該協議實用且可立即部署。我們計劃在 2025 年第一季度至第二季度啟動測試網。

我們的實現在投票者端使用了 Circom 和 SnarkJS，支持從任何設備進行投票，包括智能手機和網絡瀏覽器。對於排序器，我們使用 Gnark 和曲線 BLS12-377 和 BW6-761 來實現投票聚合中的原生遞歸。此設置生成最終的 BN254 證明，可在以太坊上進行驗證。

我們專注於去中心化，設計了可在可訪問機器（具有 64 GiB 內存的基於 CPU 的系統）上運行的排序器，這樣參與就不需要專門的硬件。

演員

組織者設置並管理投票流程，定義投票選項、持續時間和選民登記（人口普查）等參數。

選民通過用戶友好的界面與系統交互，使他們能夠安全、私密地投票。選民生成 zkSNARK 來證明他們的加密投票符合投票規則，而不會透露他們的選擇。

排序器是專門負責收集投票、驗證投票有效性和更新共享狀態的節點。它們參與分佈式密鑰生成 (DKG) 協議，以協作方式生成加密密鑰，而無需任何一方控制私鑰。

圖像1383×1076 37.2 KB

特性

使用同態加密來維護隱私。投票使用橢圓曲線上的 ElGamal 密碼系統進行加密，允許彙總加密投票而無需解密單個選票，從而保證選民選擇的機密性。

完整性通過去中心化排序器網絡的協作來保證，排序器維護一個共享狀態，該狀態由 Merkle 樹表示，總結了投票過程的當前狀態，包括累積投票和無效投票，以防止重複投票。每次用新投票更新狀態時，排序器都會生成 zkSNARK 證明，證明狀態轉換的有效性。

通過防止選民向第三方證明他們如何投票，從而降低脅迫和賄選風險，可以實現無收據性。這是通過選票重新加密和選票覆蓋機制實現的。當選民提交加密選票時，序列器會在將其存儲在州內之前對其進行重新加密，這使得在計算上無法將原始密文和重新加密的密文聯繫起來。選民還可以覆蓋他們的選票；如果選民投了一張新票，序列器會從計票中減去之前的加密選票並添加新的選票。序列器定期對隨機選票進行重新加密可以隱藏覆蓋發生的時間，通過使選票是被覆蓋還是簡單地重新隨機化而無法區分，增強了無收據性。

端到端工作流程

1. 流程初始化：組織者定義投票參數（包括選項、持續時間和人口普查），並通過智能合約在以太坊區塊鏈上註冊新流程。
2. 分佈式密鑰生成 (DKG) ：序列器協作執行 DKG 協議以生成集體公鑰加密密鑰，而無需任何一方知道私鑰。生成的公鑰在鏈上發佈，供選民在加密選票時使用。
3. 選民準備：選民從人口普查登記處檢索公共加密密鑰及其包含證明（Merkle 證明）。
4. 投票：選民選擇他們的選擇並使用公鑰加密選票。生成 zkSNARK 證明以證明其加密投票的有效性，而無需透露他們的選擇。加密的選票和證明將提交給排序器進行處理。
5. 投票收集和驗證：序列器驗證 zkSNARK 證明，以確保每次投票都符合協議規則。確認投票者符合投票資格且尚未投票，或適當處理投票覆蓋。有效的加密投票以同態方式聚合，無需解密即可進行計票。序列器更新狀態 Merkle 樹以反映新投票和無效符。
6. 狀態轉換和證明提交：Sequencers 創建 zkProofs 來證明從前一個狀態到新狀態轉換的有效性。新的根和相應的證明被提交給以太坊智能合約。合約驗證數據並更新存儲的狀態根。
7. 數據可用性：重建狀態所需的數據被髮布到數據可用性層（以太坊數據塊），確保可以驗證和重建新狀態。
8. 流程最終確定：在投票期結束時，流程在鏈上最終確定，不再接受進一步的投票。
9. 結果解密：排序器協作使用閾值解密協議解密彙總投票總數。解密結果在鏈上發佈，提供不可改變且透明的結果。

門限同態加密

該系統採用橢圓曲線 bn254 上的 ElGamal 門限加密方案，該方案提供了安全聚合投票所必需的加性同態性質。

加密

投票者的選擇表示為消息m \in \mathbb{Z}_q m ∈ Z q 。要加密投票：

1. 投票者將消息編碼為橢圓曲線上的一個點： M = m G。M = m G。
2. 投票者選擇一個隨機標量k \in \mathbb{Z}_q^* k ∈ Z ∗ q 。
3. 密文計算如下： C = (C_1, C_2) = (k G, M + k H) 。C = ( C 1 , C 2 ) = ( k G , M + k H ) 。

同態加法

橢圓曲線上的 ElGamal 密碼系統支持以點表示的消息的加法同態。給定兩個密文(C_1^{(1)}, C_2^{(1)}) ( C ( 1 ) 1 , C ( 1 ) 2 )和(C_1^{(2)}, C_2^{(2)}) ( C ( 2 ) 1 , C ( 2 ) 2 ) ，它們的分量相加可得出：

• C_1^{(\text{sum})} = C_1^{(1)} + C_1^{(2)} C ( sum ) 1 = C ( 1 ) 1 + C ( 2 ) 1
• C_2^{(\text{sum})} = C_2^{(1)} + C_2^{(2)} C ( sum ) 2 = C ( 1 ) 2 + C ( 2 ) 2

聚合密文解密為消息的總和： M^{(\text{sum})} = M_1 + M_2 M ( sum ) = M 1 + M 2

閾值解密

投票期結束後，排序器協作解密聚合密文。每個排序器P_j P j計算部分解密份額：

1. 計算： D_j = s_j C_1。D j = s j C 1 。
2. 使用拉格朗日插值係數\lambda_j λ j組合部分解密：
   D = \sum_{j \in T} \lambda_j D_j = s C_1 D = ∑ j ∈ T λ j D j = s C 1
   其中T T是至少t個序列器的集合。
3. 通過計算可以恢復明文消息：
   M = C_2 - D = M + k H - sk G = M M = C 2 − D = M + k H − sk G = M
4. 最終結果m m是通過求解M = m G M = m G得到的，得出m m 。

分佈式密鑰生成 (DKG)

為了消除對可信機構的需求，選票加密所用的加密密鑰由排序器通過分佈式密鑰生成協議協作生成，其過程如下：

1. 初始化：令G G為素數階為q q的橢圓曲線群的生成器，預先定義閾值t t和序列器數量n n ，其中t \leq n t ≤ n 。
2. 秘密共享：每個序列器P_i P i隨機選擇一個度為t - 1 t − 1的秘密多項式f_i(x) f i ( x ) ，其中f_i(0) = a_{i,0} f i ( 0 ) = a i , 0 ，係數a_{i,j} a i , j從\mathbb{Z}_q Z q中均勻隨機選擇。
3. 承諾：每個序列器發佈對其多項式係數的承諾： C_{i,j} = a_{i,j} G \quad \text{for} \quad j = 0, \ldots, t - 1. C i , j = a i , j G為了j = 0 ， … ， t − 1。
4. 份額分配：序列器P_i P i為每個其他序列器P_j P j計算份額： s_{i,j} = f_i(j), \quad \text{for} \quad j = 1, \ldots, n s i , j = f i ( j ) ，為了j = 1 , … , n
   這些共享使用 ECIES 的簡化版本安全地傳輸到相應的序列器。
5. 驗證：每個序列器P_j P j通過檢查以下內容來驗證收到的份額s_{i,j} s i , j ： s_{i,j} G \stackrel{?}{=} \sum_{k=0}^{t - 1} C_{i,k} \cdot j^k s i , j G ? = ∑ t − 1 k = 0 C i , k ⋅ j k
6. 私鑰份額計算：每個序列器計算其私鑰份額： s_j = \sum_{i=1}^n s_{i,j} \mod q s j = ∑ n i = 1 s i , j模式問
7. 公鑰計算：集體公鑰計算如下： H = \sum_{i=1}^n C_{i,0} = s G H = ∑ n i = 1 C i , 0 = s G ，其中s = \sum_{i=1}^n a_{i,0} \mod q s = ∑ n i = 1 a i , 0模式q是僅以排序器之間分佈式形式知曉的聚合私鑰。

投票

投票由以下列出的幾個部分和機制組成。

進程標識符：投票進程的唯一標識符\text{ProcessId} ProcessId 。這可確保投票與特定投票事件正確關聯，並防止跨進程干擾。

人口普查證明：Merkle 證明表明選民已被列入授權選民登記冊（人口普查）。此證明允許排序器驗證選民的資格，而無需透露整個選民名單，從而保護隱私和效率。

身份承諾：投票者使用加密哈希函數計算承諾： C = Hash(\text{Address} \parallel \text{ProcessId} \parallel s) C = H a s h ( Address ∥ ProcessId ∥ s ) ，其中H H是加密哈希函數， \text{Address} Address是投票者的唯一標識符（例如公鑰或地址）， s s是隻有投票者知道的秘密。

通過將秘密s s納入承諾C C ，我們有效地將無效符與公開數據中選民身份的任何直接關聯分離。這意味著，即使未來的量子計算進步會破壞 ElGamal 加密並洩露加密選票的內容，也沒有切實可行的方法可以使用無效符將解密的選票鏈接回特定選民的地址。

無效符：為了防止重複投票和處理投票覆蓋，投票者計算一個無效符： N = Hash(C \parallel s) N = H a s h ( C ∥ s ) 。無效符充當一次性令牌，唯一地代表投票者的參與，但不透露其身份。

通過避免在計算無效符時使用私鑰或確定性簽名，我們確保與硬件錢包和非確定性簽名方案的兼容性。

選票：選票代表選民的選擇，是一系列個人選擇，必須遵守組織者定義的選票協議規則。這種靈活的方法使協議能夠支持各種投票配置，包括範圍投票、排名、二次投票等。

假設組織者想要實施具有以下參數的二次投票系統：

• 最大選擇數：最多可以選擇 5 個選項。
• 值範圍：每個選擇必須是非負整數。
• 總成本限制：選擇的平方和不得超過 100 個信用的預算。
• 唯一值約束：允許重複值。

該協議將強制執行選票\mathbf{m} = (m_1, m_2, \ldots, m_5) m = ( m 1 , m 2 , … , m 5 ) ：

• 每個m_i \geq 0 m i ≥ 0 。
• \sum_{i=1}^5 m_i^2 \leq 100 ∑ 5 i = 1 m 2 i ≤ 100 .

加密選票：選民使用同態 ElGamal 加密方案加密選票，具體步驟如下：

• 選民的選擇被編碼成消息向量\mathbf{m} = (m_1, m_2, \ldots, m_n) m = ( m 1 , m 2 , … , m n ) ，其中每個m_i m i對應選票數組中的一個選擇。
• 每個元素m_i m i被編碼為橢圓曲線上的一個點： M_i = m_i G M i = m i G ，其中G G是曲線的生成器。
• 投票者選擇一個隨機標量k \in \mathbb{Z}_q^* k ∈ Z ∗ q ，其中q q是曲線的階。
• 密文計算如下： C = (C_1, C_2) = \left( k G,\; \sum_{i=1}^n M_i + k H \right) C = ( C 1 , C 2 ) = ( k G , ∑n i = 1 M i + k H )​
  其中H H是從分佈式密鑰生成協議獲得的公鑰。

零知識證明（zkSNARK） ：選民生成一個 zkSNARK，在不透露選票內容的情況下證明：

• 正確的加密：加密選票根據加密方案正確形成。
• 協議合規性：投票者的選擇遵守組織者定義的投票協議規則。
• 正確的無效符和承諾：使用投票者的秘密s和地址正確計算無效符和承諾。
• 秘密知識：投票者知道秘密s和加密中使用的隨機標量k k 。

簽名：投票者使用與其地址關聯的私鑰簽署投票的必要部分。這將驗證投票，並以可驗證的方式將其與投票者的身份綁定。可以支持多種簽名方案（ECDSA、EdDSA、RSA 等）。

狀態轉換

狀態 Merkle 樹是一種加密數據結構，可以高效安全地驗證其所包含的數據。該樹的結構用於在預定義的索引或地址中存儲各種類型的信息：

• 過程參數：存儲在靜態索引中，包含必要信息，例如\text{ProcessId} ProcessId 、人口普查 Merkle 樹的根（ \text{censusRoot} censusRoot ）、投票協議配置，以及通過 DKG 協議生成的公鑰加密密鑰H H 。
• 結果累加器：維護兩個累加器來處理投票的加減：
  • 加法累加器（ C_{\text{add}} C add ）：存儲已添加到計票中的同態聚合加密投票。
  • 減法累加器（ C_{\text{sub}} C sub ）：存儲由於投票覆蓋而減去的同態聚合加密投票。
• 無效符：存儲以防止重複投票。每個無效符N N都與投票者的承諾相關聯，並且對於特定投票流程而言對於該投票者是唯一的。
• 承諾：存儲以跟蹤選民參與情況並方便覆蓋投票。

排序器負責處理新的投票並更新共享狀態。每個狀態轉換涉及以下步驟：

1. 批量收集選票：排序器從投票者那裡收集一批最多N N個新選票。批量投票可提高效率和可擴展性，使排序器能夠同時處理多個選票。N N的值由平衡計算約束和網絡吞吐量的系統參數決定。

2. 投票驗證：對於批次中的每個投票，排序器執行：

   • zkSNARK 證明驗證：確保每次投票提交的零知識證明有效，並且投票符合協議規則，包括正確的加密、遵守投票協議約束以及正確計算無效器和承諾。
   • 資格檢查：通過檢查提供的人口普查 Merkle 證明與州內存儲的\text{censusRoot} censusRoot來驗證選民的資格。
   • 防止雙重投票：檢查否決符N N是否已存在於該州。如果不存在，則該投票將被視為新投票。如果存在，則該投票被視為投票覆蓋。

3. 處理投票覆蓋：如果投票者使用相同的無效符N N提交新投票，則排序器：

   • 從減法累加器C_{\text{sub}} C sub中減去之前的加密投票。
   • 將新的加密投票添加到加法累加器C_{\text{add}} C add 中。
   • 取代州內新的加密選票。

4. 隨機重新加密：為了增強無收據性並防止選票和選民之間的聯繫，序列器對現有的加密選票進行隨機重新加密：

   • 選擇該州加密選票的隨機子集。
   • 使用新的隨機標量，通過添加零加密來重新加密每個選定的選票。
   • 使用重新加密的版本更新該州的加密選票。

5. 投票的同態聚合：序列器使用 ElGamal 加密的同態性質來更新累加器：

6. 狀態轉換的生成 zkSNARK ：sequencer 生成一個 zkSNARK 證明，證明從前一個根\text{Root1} Root1到新根\text{Root2} Root2的狀態轉換的有效性。zkSNARK 證明驗證了所有先前的約束和操作。

7. 鏈上提交：排序器提交：更新後的狀態根\text{Root2} Root2 。狀態轉換有效性的證明。對包含投票和狀態更新的數據 blob 的哈希承諾，確保數據可用性。

Vocdoni 代幣 (VOC)

Vocdoni 推出了一種新代幣 (VOC)，以協調參與者之間的激勵機制並確保去中心化投票生態系統的可持續性。該代幣具有多種基本功能：激勵排序器、促進投票流程的支付並實現去中心化治理。

排序者必須質押代幣作為抵押品才能參與網絡，從而促進誠實行為和網絡安全。他們根據對處理有效投票和維護網絡完整性的貢獻獲得 VOC 代幣獎勵。

組織者使用代幣支付創建和管理投票流程的費用。成本取決於多種因素，例如最大投票數（ \text{maxVotes} maxVotes ）、投票時長（ \text{processDuration} processDuration ）以及所需的安全級別，這與參與排序器的數量有關。

投票過程的總成本使用以下公式計算：

\text{總成本} = \text{基礎成本} + \text{容量成本} + \text{持續時間成本} + \text{安全成本}總成本=基礎成本+容量成本+持續時間成本+安全成本

成本組成部分：

• 基本成本： \text{baseCost} = \text{fixedCost} + \text{maxVotes} \cdot p baseCost = fixedCost + maxVotes ⋅ p ，其中\text{fixedCost} fixedCost是固定費用， p p是一個較小的線性因子。

• 容量成本： \text{capacityCost} = k_1 \left( \frac{\text{totalVotingProcesses}}{\text{totalSequencers} - \text{usedSequencers} + \epsilon} \cdot \text{maxVotes} \right)^a capacityCost = k 1 ( totalVotingProcesses totalSequencers − usedSequencers + ϵ ⋅ maxVotes ) a ，其中k_1 k 1是縮放因子， a a控制非線性， \epsilon ϵ是一個較小的數，以防止被零除。

• 持續時間成本： \text{durationCost} = k_2 \cdot \text{processDuration}^b durationCost = k 2 ⋅ processDuration b ，其中k_2 k 2作為縮放因子， b b根據持續時間控制縮放。

• 安全成本： \text{securityCost} = k_3 \cdot e^{c \left( \frac{\text{numSequencers}}{\text{totalSequencers}} \right)^d} securityCost = k 3 ⋅ e c ( numSequencers totalSequencers ) d ，其中k_3是比例因子， c c , d d控制與所用序列器數量相關的指數比例。

排序器根據處理的投票數和投票重寫次數（包括無收據的重新加密）獲得獎勵。排序器i i的總獎勵計算如下：

\text{sequencerReward}_i = R \left( \frac{\text{votes}_i}{\text{maxVotes}} \right) + W \left( \frac{\text{voteRewrites}_i}{\text{totalRewrites}} \right ) sequencerReward i = R ( votes imaxVotes ) + W ( voteRewrites i總重寫數）

但受到以下限制：

\frac{\text{voteRewrites}_i}{\text{votes}_i} \leq T voteRewrites i投票i ≤ T且R > W R > W

確保排序器優先處理新投票而不是重寫。這裡， R R和W W分別是分配給處理投票和投票重寫的獎勵池的一部分， T T是限制每個投票重寫次數的預定義常數。

未能履行義務的排序者可能會被削減抵押品，計算方法如下：

\text{SlashedAmount}_i = s \cdot \text{StakedCollateral}_i SlashedAmount i = s ⋅ StakedCollat eral i

其中s s是削減係數（ 0 \leq s \leq 1 0 ≤ s ≤ 1 ）。

資源

• 白皮書完整版： https://whitepaper.vocdoni.io

• 正在實施該協議的 MVP 版本的存儲庫列表：

  • 用於投票者的 Circom 電路GitHub - vocdoni/z-ircuits：Vocdoni Z snark 電路。
  • 序列器加密原語GitHub - vocdoni/gnark-crypto-primitives：用 Gnark 編寫的一組自定義電路，支持 Vocdoni 上的匿名投票。
  • Circom 到 Gnark 解析器GitHub - vocdoni/circom2gnark:Circom 到 Gnark Groth16 解析器和遞歸示例
  • ElGamal 和 DKG 沙盒： GitHub - vocdoni/vocdoni-z-sandbox

• 聯繫方式：pau [at] vocdoni [dot] io

• Discord： https://chat.vocdoni.io