格拉姆斯特丹方程

07-17

本文為機器翻譯

展示原文

格拉姆斯特丹方程

非常感謝@potuz對模型的反饋。也感謝@barnabe和@terence 。

概述

Glamsterdam 方程旨在指導在較短時隙時間的背景下，選擇延遲執行還是ePBS 。基於一組基本假設，計算兩種時隙流水線配置的最大執行 gas/秒和 blob/秒。然後，根據用戶在擴展性、時隙時間、簡單性和無需信任性之間的優先級，計算出一個效用最大化的時隙配置。Glamsterdam 方程應被視為一種工具。它本身無法在辯論中給出明確的答案，原因有二：

一些建模決策可能會使結果偏向任一方向。為了生成易於概覽的方程式，我們進行了某些簡化。常數的選擇是基於合理的推測，調整後可能會產生不同的結果。
我們對效用方程中較為主觀的常數持有不同的看法。諸如去信任化交易所的價值或簡潔設計等主觀特質並未被量化，用戶只需在U_O U O中提供其主觀量化值即可。他們還可以通過效用彈性來指定不同擴展組件的重要性。

整體 Glamsterdam 效用函數指定為

U = (G^*_s)^{U_G} \乘以 (B^*_s)^{U_B} \乘以 (1/S^*)^{U_S} \乘以 U_O，

U = （ G ∗ s ） UG × （ B ∗ s ） UB × （ 1 / S ∗ ） US × UO ，

依賴於Fusaka在gas/s（ G^*_s， G ∗ s ）和blobs/s（ B^*_s， B ∗ s ）上的比例縮放，以及時隙時間S^* S ∗的相對減少。指數是效用彈性（默認值為1），指定了不同縮放組件的重要性。本文將首先分析推導延遲執行和ePBS在不同時隙時間（遵循簡化假設）下可實現的縮放，然後返回效用函數。然後改變常數以分析不同假設和優化下的結果。最後，探索替代設計。

常量

以假設的 Fusaka 基線為起點，首先在以下常數下分析時隙流水線方程：

象徵	價值	解釋
L_G L G	0.8秒	全局延遲。最小區塊充分傳播以形成共識所需的時間。
L_D L D	0.8秒/MB	數據延遲。每 MB 數據完整傳播所需的額外時間。
L_{RF} L R F	0.2秒	中繼延遲。修復了將信標塊發送到中繼時的延遲問題。
L_{RD} L R D	0.15秒/MB	中繼數據延遲。將信標塊發送到中繼時，每 MB 數據所需的額外時間。
b_b b b	1 MB	信標區塊大小。必須容納的信標區塊的最大大小。
P_{bg} P b g	每 60M gas 消耗 1MB	每種 Gas 的有效載荷字節數。每種 Gas 的有效載荷的最大數據大小。
E_s E s	60M gas/s	執行速度。每秒可執行的最大 gas 量。
B_r B r	15 個 blob/秒	斑點速率。每秒可傳播的最大斑點數量（源自 48 個斑點/ 4-L_G4 - L G秒）。
\bar{S } ¯S	12秒	基線槽長度。Fusaka基線槽長度。
\bar{G } _s¯G s	5M gas/s	基線最大 gas 吞吐量。效用函數中用作參考點的基線最大 gas/s（60M gas/12 秒）。
\bar{ B } _s¯Bs	4 個斑點/秒	基線 blob 吞吐量。效用函數中用作參考點的基線 blob/s（48 blob/12 秒）。
A_a A a	3秒	證明聚合時間。完整證明聚合所需的時間。
\mathrm{PTC}_d P T C d	1.4秒	Blob PTC 延遲。PTC投票在時隙結束時傳播所需的裕度。
A_d A d	0.4秒	構建器延遲。構建器在最壞情況下，在認證截止日期之後等待的時間，之後才會在 ePBS 中發佈有效載荷。

總中繼延遲定義為L_R=L_{RF} + b_\text{b}L_{RD} L R = L R F + b b L R D ，其中整個帖子都使用L_R L R ，而不是寫出各個組件。

常數是根據先前的分析和當前發展做出的有根據的猜測，例如： 1、2、3、4、5、6、7、8、9 。不確定性較高的常數的影響有時可能會被平均化，從而產生更切合實際的結果。例如，數據延遲L_D L D可能略顯保守，而每gas 的有效載荷字節數P_{bg} P b g則較為激進，這假設數據成本會進一步調整。為了幫助讀者形成個人觀點，請參考以下公式：

運行分析和繪製圖表的源代碼將在網上發佈（本週末），
結論部分探討了基線設置的變化。

值得強調的一個具體簡化分析是，在點對點層，blob 和區塊傳播之間的交互沒有建模，而信標區塊和有效載荷傳播之間的交互則進行了建模。每個時隙的 blob 數量僅根據 Fusaka 規範中規定的可用傳播時間（取決於時隙結構）得出，其中包括與區塊相同的全局延遲L_G L G。這使得分析更加易於處理。考慮到各種驗證者角色以及 CL/EL 交互，blob 如何與區塊交互仍然是一個懸而未決的問題。

延遲執行

延遲執行採用簡單配置，沒有特殊的頭部截止時間，並且 blob 必須在證明時可用。分析的目標是設置證明截止時間A A以最大化效用，該效用是 gas 和 blob 吞吐量的函數。一個 slot 中可包含的總 gas G G受執行時間和傳播時間的限制。有效載荷傳播的固定時間約束可以表示為

c = L_R + L_G + b_\text{b}L_D，

c = LR + LG + bbLD ，

包括中繼延遲、全局延遲以及信標塊的傳播（消耗固定帶寬，且無法同時用於有效載荷）。給定 gas 量G時，最大有效載荷大小為P_{bg}G P b g G字節，其中P_{bg} P b g是每單位 gas 的最大有效載荷大小。傳播此有效載荷的時間取決於可用窗口Ac A − c ，從而得出以下約束：

G \le \frac{Ac}{P_{bg} L_D}。

G≤A − cPbgLD 。

Gas 還受到執行窗口SA S − A和執行速度E_s E s (gas/s) 的限制，從而給出第二個約束：

G \le E_s(SA)。

G≤Es （ S - A ）。

當G G的兩個限制相等時，可以找到最大化潛在 gas 吞吐量的截止時間A_G A G ：

E_s(S-A_G) = \frac{A_G-c}{P_{bg} L_D}。

E s （ S − A G ） = A G − c P b g L D 。

求解A_G A G得出：

A_G = \frac{c + E_s P_{bg} L_D S}{1 + E_s P_{bg} L_D}。

A G = c + E S P b g L D S 1 + E S P b g L D 。

然而，總體目標是最大化效用，其中也包括 blob 吞吐量。將一個 slot 中的 blob 總數定義為B。效用函數的縮放項分別定義為 gas/s 和 blob/s 相對於當前基線（以條形突出顯示）的變化：

G_s^* = \frac{G/S}{\bar{G}_s}, \;\;\;\;\;\; B_s^* = \frac{B/S}{\bar{B}_s}。

G ∗ s = G / S¯Gs ， B ∗ s = B / S¯ B s 。

效用最大化截止日期A_U A U是通過最大化整體效用函數的縮放項的乘積來找到的：

U_2 = (G^*_s)^{U_G} \times (B^*_s)^{U_B}。

U2 = （ G ∗ s ） UG × （ B ∗ s ） UB 。

一個有用的假設是，所尋求的最優解是執行受限的（即G \propto SA G ∝ S − A ），因為較晚的截止時間總是能提高 blob 的吞吐量。為了找到這個最優解，對數效用\ln U_2 ln對U 2進行分析。忽略不影響A A導數的常數項，該函數簡化為：

\ln U_2 = \text{const} + U_G \ln(SA) + U_B \ln(A - L_G - L_R)。

在…中U 2 = const + U G ln （ S − A ） + UBln （ A − LG − LR ）。

對A A取導數可得：

\frac{d}{dA}(\ln U_2) = -\frac{U_G}{SA} + \frac{U_B}{A-L_G-L_R}。

d d A （對數U 2 ) = − U G S − A + U B A − LG − LR 。

將導數設為零並求解A A可得出最終表達式：

A_U = \frac{U_B S + U_G (L_G+L_R)}{U_G + U_B}。

AU = UBS + UG （ LG + LR ） UG + UB 。

然後，通過選擇這兩個候選者中的較晚者來選擇最終的最佳截止期限A^* A ∗ ，該期限受允許進行證明聚合的最新可接受截止期限的限制， A_L = S - A_a A L = S − A a ：

A^* = \min(\max(A_G, A_U), A_L)。

A * = min ( max ( AG , AU ) , AL ) 。

一旦選定了最終期限A^* A ∗ ，則在該期限內可實現的總絕對氣體G G可以通過取兩個限值中的最小值來計算：

G = \min\left(E_s(SA^*)，\frac{A^*-c}{P_{bg} \cdot L_D}\right)。

G = min （ Es （ S - A ∗ ）， A ∗ -cPbg⋅LD ）。

由此得出最終的吞吐量。每秒的Gas為：

G_s = G/S，

Gs = G / S ，

每秒的 blob 數量由截止期限A^* A ∗和 blob 傳播速率B_r B r決定，為：

B_s = \frac{(A^*-L_G-L_R) \cdot B_r}{S}。

Bs = （ A ∗ −LG − LR ） ⋅BrS 。

圖 1 顯示了最佳證明截止期限，該期限可以是：

有效載荷傳播時間和執行時間之間的完美平衡（ A_G A G ；洋紅色），
當忽略有效載荷傳播時間的限制時，效用達到最優（ A_U A U ；紅色），
在允許證明聚合的最新點（ A_L A L ；紫色）。

圖 1

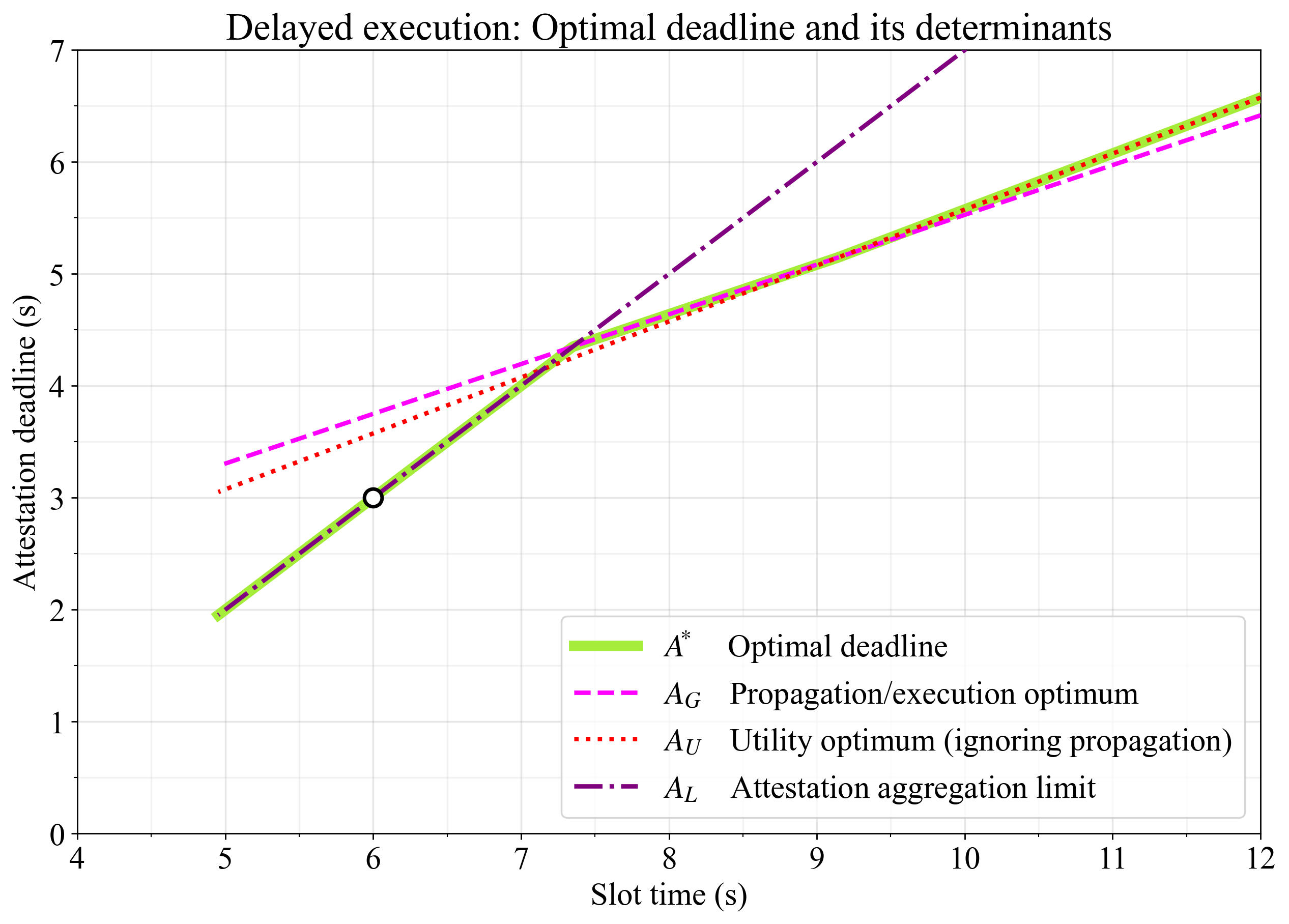
圖 1.延遲執行中的最佳截止時間，即傳播/執行 gas 最優值A_G A G ，純執行受限模型中效用最大值A_U A U ，以及允許進行證明聚合的最新點A_L A L 。圓圈表示在 6 秒的時隙中，3 秒的證明截止時間的潛在目標。為了實現最佳吞吐量，這需要進行一些優化以縮短傳播時間（將優化線向下推）。

使用默認常量，當時隙長度為 12 秒時，最佳截止時間約為 6.5 秒（ A_U A U機制）。在時隙時間低於 9 秒左右時，有效載荷傳播時間會限制 Blob 和執行的效用最優值，因此必須通過選擇更晚的證明截止時間（ A_G A G機制）來做出妥協。當時隙時間低於 7.3 秒左右時，在A_G A G下將不再有足夠的時間進行證明聚合，並且必須通過選擇更早的截止時間（ A_L A L機制）來犧牲吞吐量（傳播）。在 6 秒時隙時間下延遲執行的實現可能會將目標鎖定在 3 秒的證明截止時間（正如已經提出的）。為了在 6 秒時實現高吞吐量，必須通過以下優化來加快傳播速度（下推圖 1 中的優化線）：

使得通話數據更加昂貴，
改進 p2p 層，
實施多維費用市場或宏觀定價（以限制最壞情況的有效載荷大小）。

還可以假設構建者自己可以選擇有效載荷組合，以平衡任何給定截止期限的傳播和執行，從而為早期截止期限留出餘地。然而，對於字節數較大的有效載荷，這會給有效載荷傳播帶來壓力。即使遵守 Gas Limit，此類有效載荷也可能無法被接受。這也是多維費用市場如此有吸引力的原因之一。

電子PBS

在對 ePBS 進行建模時，使用雙截止期限方法，允許最佳有效載荷 PTC 截止期限\mathrm{PTC}_P P T C P，同時將 PTC DA 截止期限保持在時隙的最晚可能點

\mathrm{PTC}_B=S-\mathrm{PTC}_d。

PTCB = S − PTCd 。

有效載荷在無需信任的環境中發佈，在最壞的情況下，構建者必須在證明截止日期之後發佈有效載荷A_d A d 。附錄 A 中討論了將A_d A d納入分析的相關性。blob 的發佈時間設置為c c ，這樣構建者就無需等待A_d A d完成證明計數後再發布，從而允許稍長一些的傳播時間。ePBS 中的證明截止日期設置得比延遲執行中的早，具體為常數c c ：

A = c = L_G + b_b L_D。

A = c = LG + b b L D。

然後，有效載荷在c+A_d c + A d處釋放，並在傳播時繼承其自身的全局延遲L_G L G 。剩下的唯一任務是計算有效載荷的最佳 PTC 截止時間\mathrm{PTC}_P P T C P ，該截止時間嚴格定義為使總 gas 值G G最大化的點。

gas 的數量受執行窗口S-\mathrm{PTC}_P S − P T C P和執行速度E_s E s (gas/s) 的限制：

G \le E_s(S-\mathrm{PTC}_P)。

G≤Es （ S - PTCP ）。

它還受到傳播有效載荷所需時間的限制。一筆包含 Gas G的有效載荷最多需要L_G + (G \cdot P_{bg} \cdot L_D) L G + ( G ⋅ P b g ⋅ L D )才能傳播，並且必須允許其最遲在\mathrm{PTC}_P P T C P截止時間到達：

c + A_d + L_G + (G \cdot P_{bg} \cdot L_D) \le \mathrm{PTC}_P。

c + A d + LG + ( G ⋅ P b g ⋅ L D ) ≤ P T C P 。

這給出了傳播過程中的氣體約束：

G \le \frac{\mathrm{PTC}_P - c - A_d - L_G}{P_{bg}L_D}。

G≤PTCP - c - Ad - LGPbgLD 。

當G G的兩個限制相等時，可以找到最佳截止日期\mathrm{PTC}^*_P P T C ∗ P ：

E_s(S-\mathrm{PTC}_P) = \frac{\mathrm{PTC}_P - c - A_d - L_G}{P_{bg}L_D}。

E s （ S - P T C P ） = P T C P - c - A d - L G P b g L D 。

對\mathrm{PTC}_P P T C P求解並通過\mathrm{PTC}_B P T C B進行鉗位可得出最終方程：

\mathrm{PTC}^*_P = \min\Bigg(\mathrm{PTC}_B, \;\frac{c + A_d + L_G + E_s P_{bg} L_D S}{1 + E_s P_{bg} L_D}\Bigg)。

P T C ∗ P =最小值( P T C B , c + A d + LG + E s P b g L DS 1 + E s P b g L D ）。

一旦找到最佳截止時間\mathrm{PTC}^*_P P T C ∗ P ，就可以確定最終的吞吐量。每秒 gas 消耗量G_s G s由傳播約束得出：

G_s = \frac{\mathrm{PTC}_P - c - A_d - L_G}{P_{bg}L_DS}。

Gs = P T C P − c − A d − LG Pbg L D S 。

每秒的 blob 數量B_s B s由 blob 傳播的可用時間（從其在c c處發佈到 blob 截止時間\mathrm{PTC}_B P T C B ，同時考慮其自身的全局延遲 $L_G$）和 blob 速率B_r B r決定：

B_s = \frac{(\mathrm{PTC}_B - c - L_G) \cdot B_r}{S}。

Bs = （ PTCB - c - LG ） ⋅BrS 。

圖 2 顯示了在基線常數下最大化 ePBS 吞吐量的最佳截止時間。

圖 2

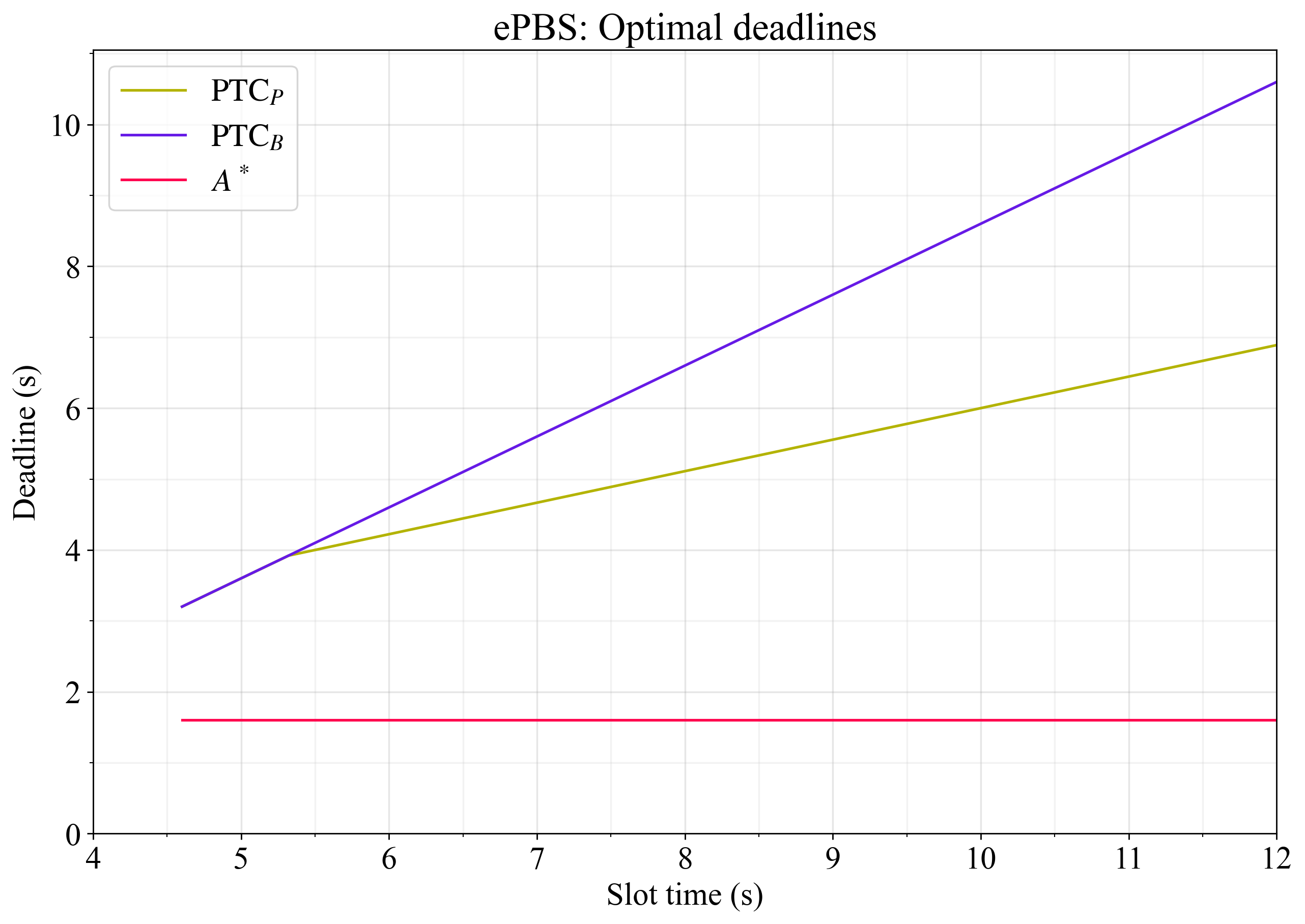
圖 2.在基線常數下，最大化 ePBS 吞吐量的最佳截止時間。有效載荷觀測截止時間\mathrm{PTC}^*_P P T C ∗ P設定在傳播和執行之間達到完美平衡的點，並遵循 PTC 在\mathrm{PTC}_B P T C B投票後無法發生的限制。

延遲執行和 ePBS 的吞吐量

圖 3 展示了延遲執行和 ePBS 的執行速率（Mgas/s 和 blobs/s）。顯然，ePBS 特別適合擴展 blobs，因為它提供了較晚的 PTC 截止時間。由於有效載荷的截止時間可以獨立設置，因此吞吐量會隨著時隙時間的縮短而平滑衰減，直到傳播時間最終被限制在 5.5 秒以下。吞吐量的平滑下降是由於以下因素的相對重要性不斷增加：

全局延遲L_G L G ，
信標塊傳播時間c c ，
構建者確定信標區塊將收集足夠的證明A_d A d所需的時間，
以及 PTC 投票傳播時間\mathrm{PTC}_d P T C d 。

延遲執行最適合在較長的時隙時間範圍內擴展 L1 gas 的使用，因為在時隙開始時產生的延遲會減少L_G-L_R+A_d L G − L R + A d ，並且使用默認常量，可以在傳播和執行之間合理地平衡證明截止時間。當證明聚合約束在 7.3 秒左右生效時，吞吐量曲線會出現一個拐點。由於在基準常量下傳播時間不足，吞吐量會大幅低於此時隙長度。

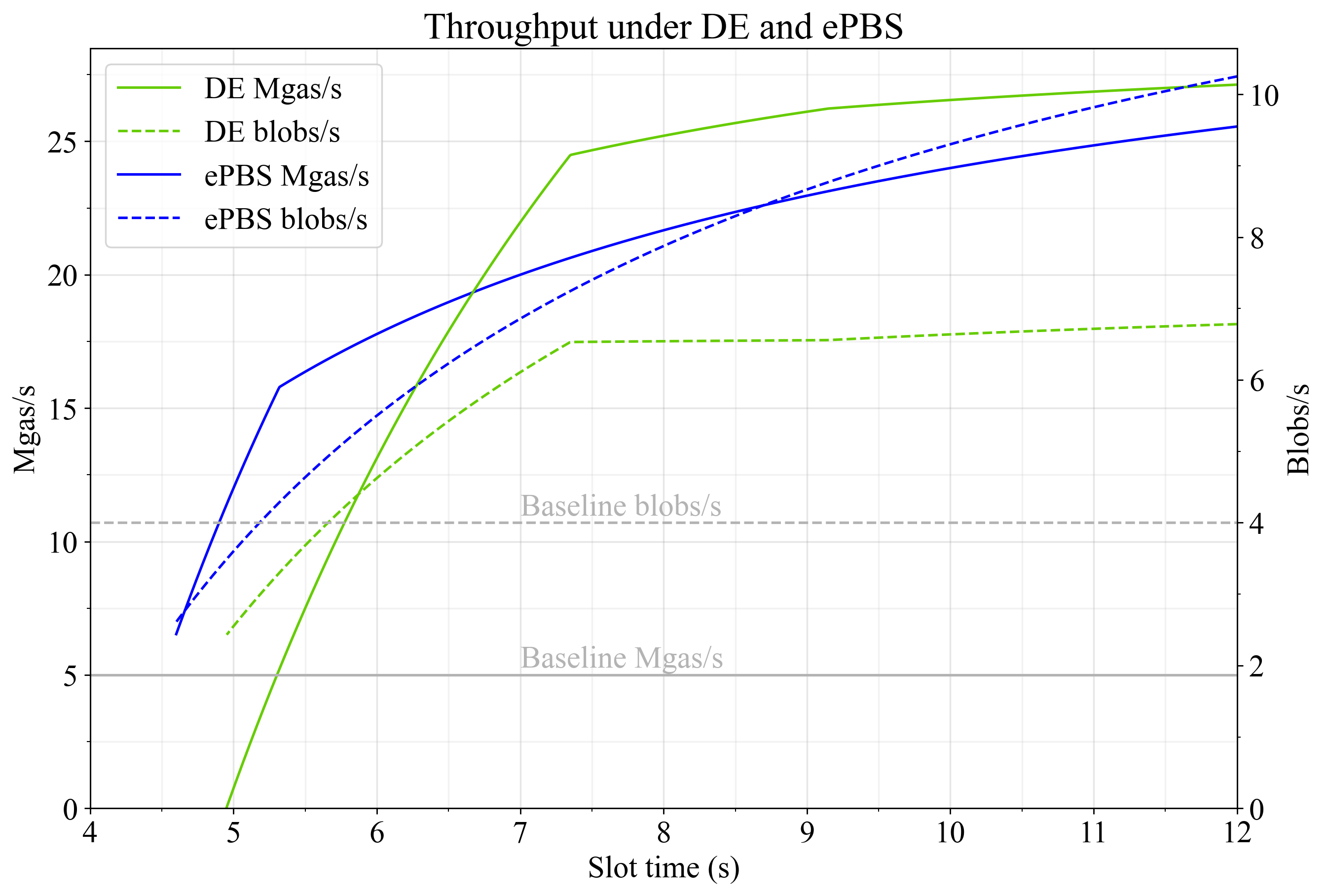
圖 3.不同時隙下延遲執行（綠色）和 ePBS（藍色）下的吞吐量，分別以 Mgas/s（實線）和 blobs/s（虛線）表示。即使在較短的時隙時間內，這兩種方法都有可能顯著擴展以太坊。

根據 Glamsterdam 方程的效用

Glamsterdam 方程捕捉了時隙重構帶來的擴展性，它考慮了時隙時間的相對變化S^* S ∗以及一個主觀縮放因子U_O U O，該因子可以反映任何其他因素。如果優先考慮不改變分叉選擇和不設置 PTC 的簡單性，則有人可能會將U_O>1 U O > 1賦給 DE。另一方面，例如，如果構建者和提議者之間的去信任支付被視為關鍵，則有人可能會將U_O>1 U O > 1賦給 ePBS。完整的方程式如下：

U = (G^*_s)^{U_G} \乘以 (B^*_s)^{U_B} \乘以 (1/S^*)^{U_S} \乘以 U_O。

U = （ G ∗ s ） UG × （ B ∗ s ） UB × （ 1 / S ∗ ） US × UO 。

該方程還包含效用彈性，用於指定效用度量中不同績效指標的重要性。效用彈性為 1 表示效用與指標成正比，而彈性為 0 表示指標與整體效用無關。這些彈性包括：

U_G U G – 執行吞吐量的效用彈性。
U_B U B – blob 吞吐量的效用彈性。
U_S U S – 較短時隙時間的效用彈性。

圖 4 展示了延遲執行和 ePBS 的效用在時隙時間的變化情況，使用了U_G=1 U G = 1 、 U_B=1 U B = 1 、 U_S=1 U S = 1和U_O=1 U O = 1 的設置。兩種重組方案帶來的效用增益大致相同，其中延遲執行在 7.3 秒時隙時間達到峰值，而 ePBS 在 10 秒時隙時間左右達到峰值。

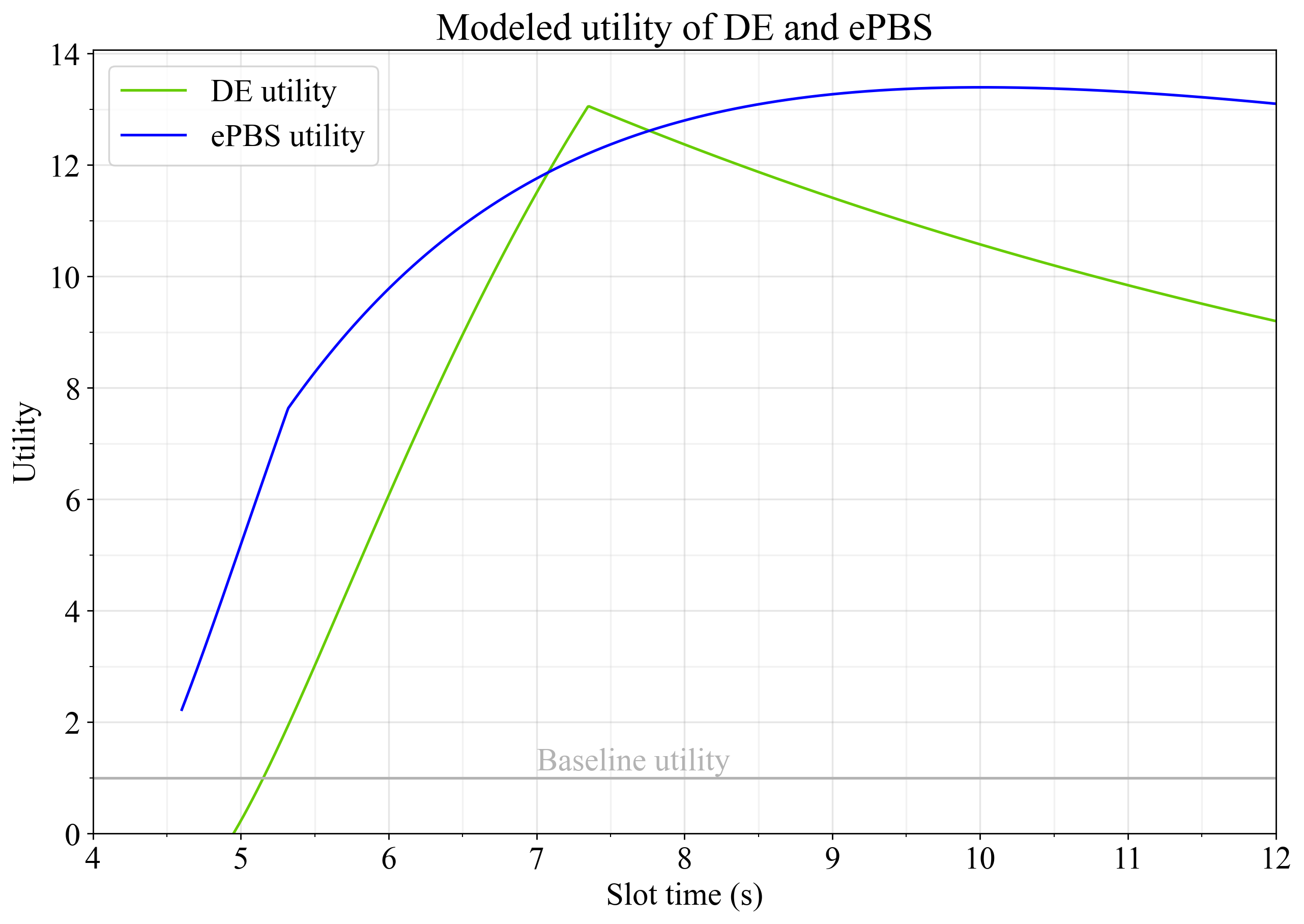
圖 4.當所有彈性都設置為 1 且U_O=1 時，延遲執行和 ePBS 的效用，兩個選項的U O = 1 。

我們對哪些指標最重要有著不同的看法，因此彈性指標也至關重要。例如，考慮到Fusaka計劃中每時隙32個blob的目標已經是一個顯著的改進，而目前6個blob的目標實際上並未消耗，因此將blob的進一步擴展的重要性賦予低於執行氣體擴展的重要性似乎是合理的。U_G =1 U G = 1和U_B=0.4 U B = 0.4的彈性指標體現了這一概念。縮短時隙時間的重要性可能介於兩者之間，例如U_S=0.7 U S = 0.7 。

圖 5 展示了這些彈性條件下的結果，由於 blob 擴展的重要性被賦予得較低，延遲執行在某種程度上更受青睞。另一方面，一些人可能認為 ePBS 本質上更優，因為它能夠促進構建者和提議者之間無需信任的合作。設置 ePBS 的U_O=1.1， U_O = 1.1體現了 ePBS 在不可衡量的品質方面比延遲執行好 10% 的概念。藍色虛線體現了這一點，並且當 ePBS 的時隙時間約為 9 秒時，或當 DE 的時隙時間約為 7.3 秒時，其效用達到最大化。

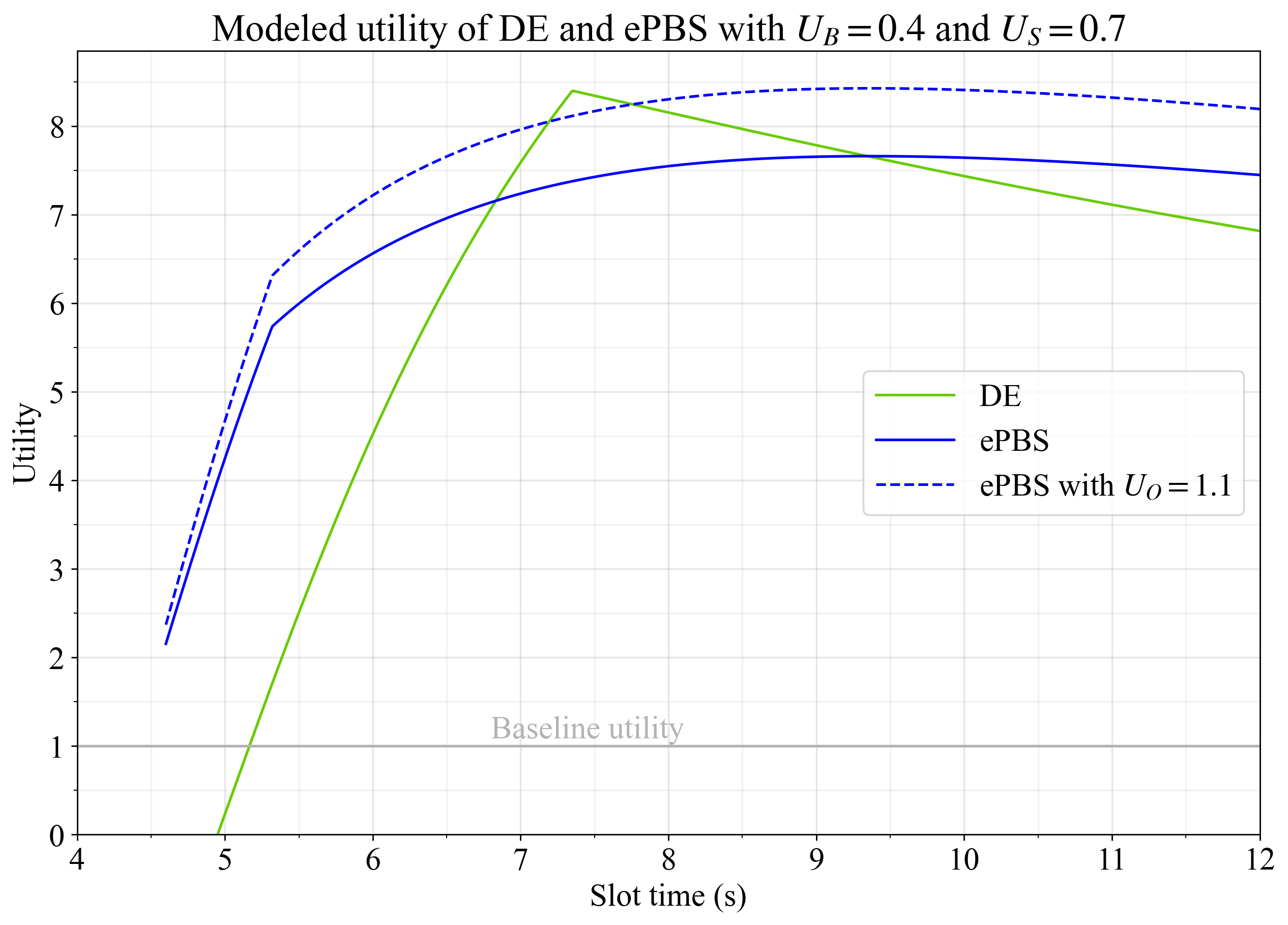
圖 5.延遲執行和 ePBS 的效用，彈性係數為U_G=1， U G = 1 ， U_B=0.4 U B

來源

免責聲明：以上內容僅為作者觀點，不代表Followin的任何立場，不構成與Followin相關的任何投資建議。

喜歡

評論