感謝Shao 、 Chih Cheng Liang和Panta Rhei的反饋和討論。
抽象的
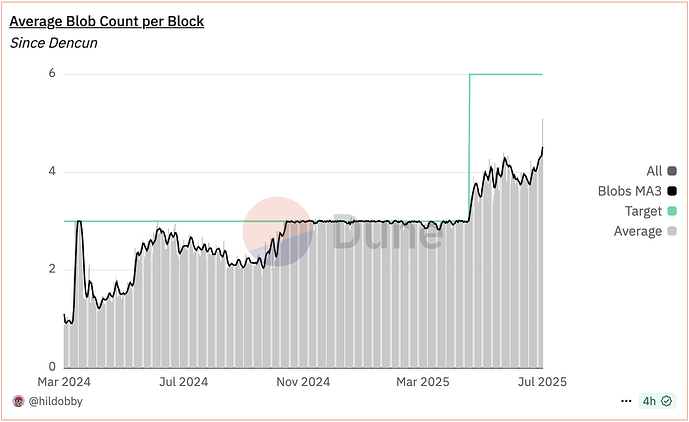
以太坊正進入大規模網絡容量擴容時期。隨著Fusaka分叉中PeerDAS的推出,blob容量將按計劃擴容至48/72。然而,由於blob需求增長跟不上供應容量,導致供應過剩,導致blob費用市場在較長時間內無法有效運作。
本提案引入了雙變量資源定價機制,作為 EIP-1559 的擴展,該機制會根據實際需求波動動態調整每base_fee_per_blob_gas和每區塊target_blob_gas_per_block 。這種方法可以穩定區塊費用,並確保區塊費用市場在整個網絡擴展階段保持有效。
動機
目前,以太坊上的資源費用會隨著網絡擁堵程度而波動,擁堵期間費用上漲,使用率低時費用下降。在有效市場中,資源稀缺性會驅動價格與供需相匹配。然而,當我們通過增加資源目標和限額來擴展網絡容量時,資源的稀缺性會導致供應過剩。由於需求沒有相應地上升到新的目標水平,價格不再反映市場均衡,變得無效。過去一年,我們已經看到了 blob 使用中這種不平衡的跡象:
- 大多數情況下,Blob 使用量低於目標值。實際上,需求不會立即響應供應變化。Blob 需求逐漸增長,達到目標消耗水平仍需時日。在此之前,
base_fee_per_blob_gas幾乎保持免費。
- 當需求接近目標水平時,每blob gas
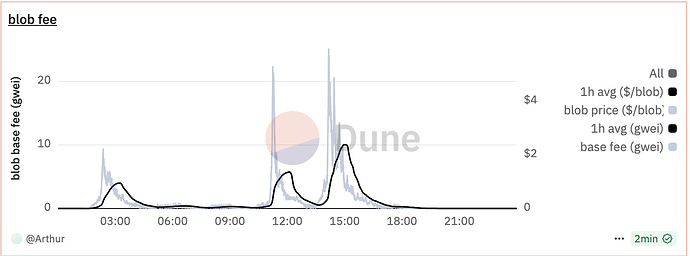
base_fee_per_blob_gas會變得非常不穩定。由於價格起始價格僅為1wei,即使blob gas使用量的微小波動也可能導致價格劇烈波動。這種波動尤其明顯,因為市場由少數主要消費者主導,他們的高blob gas使用量往往集中在同一時期,這進一步放大了價格波動並降低了可預測性。
下圖展示了 2025 年 5 月 5 日(Pectra 分叉之前)基礎費用的波動情況。數據顯示價格出現了三次飆升,但在大部分時間段內,費用幾乎保持免費。
- 每次我們提高
target_blob_gas_per_block規模,base_fee_per_blob_gas就會再次下降到 1 wei。這意味著我們會反覆遇到問題 (1) 和 (2)。當PeerDAS和BRO上線時,我們預計base_fee_per_blob_gas會在相當長的一段時間內保持為零。
雙變量 EIP-1559 機制
當前 blob 基礎費用計算如下:
b_{n+1}=b_n∗exp(\frac{g_i−T}{8T}) b n + 1 = b n ∗ e x p ( g i − T 8 T )
其中b_n b n是當前區塊的基本費用, b_{n+1} b n + 1是下一個區塊的基本費用, g_i g i是當前使用的 gas, T T是目標 blob gas,固定為 6。有關更多詳細信息,請參閱此處。
我們建議將目標 blob gas 設置為變量,以動態調整基礎費用( b_i b i )和目標費用( t_i t i )。此機制有以下用途:
- 調節目標周圍的 blob gas 使用量,這代表網絡可以長期輕鬆處理的持續容量。
- 基本費用仍作為基於網絡擁堵情況的底價。
- 當網絡擴展 blob 容量時穩定基本費用。
基本費用調整
調整基礎費用的目的是圍繞 Gas 目標值來調節 Gas 消耗量。與原版 EIP-1559 類似,調整規則根據上一個區塊的基礎費用( b_ {i-1} b i − 1 ) 、 Gas 目標值(t_{i-1} t i − 1)和已用 Gas( g_{i-1} g i − 1 ) ,使用以下公式計算當前區塊的基礎費用( b_i b i )。其中, K_b表示每單位過剩 Gas 的調整率:
b_{i+1} = b_i \, (1 + K_b \times (g_i - t_i)) b i + 1 = b i ( 1 + Kb × ( g i − t i ) )
我們可以將此方程轉換為指數形式(有關完整推導,請參閱Dankrad Feist 的帖子):
b_n = b_0 \, \exp(K_b \sum_{i=0}^{n-1} g_i - t_i) b n = b 0經驗值( K b ∑ n − 1 i = 0 g i − t i )
即使目標是一個變量而不是固定數字,公式仍然與原始公式相同。根據定義, K_b = \frac{1}{\text{基礎費用更新分數}} K b = 1基礎費用更新分數且\sum_{i=0}^{n-1} g_i - t_i = \text{Excess Blob Gas} ∑ n − 1 i = 0 g i − t i = Excess Blob Gas 。因此,我們不需要更改任何現有的實現。
基本費用敏感度
每單位過剩 blob gas 的調整率 ( K_b K b ) 提供了一種便捷的方法來考慮基礎費用的敏感性。在EIP-7691中,新的 2:3 的目標與最大比率破壞了 blob 滿用和空用場景之間對稱的響應性。這種不對稱導致base_fee_per_blob_gas在 blob 滿用的情況下增加約 8.2%,而在空用的情況下減少約 14.5%。
我們不再關注對滿載和空載 blob 使用情況的響應是否對稱,而是將對稱響應重新定義為,無論過量 gas 是增加還是減少,都對等量的過量 gas 變化應用相同的百分比調整。這種方法可確保在動態目標條件下,基礎費用敏感度保持一致。
我們建議恢復12.5%作為基礎費用的最大變化率,並使用以下公式計算K_bK b :
\exp(K_b \times \max(abs(g_i - t_i))) \approx 1.125 exp ( K b × max ( a b s ( g i − t i ) ) ) ≈1.125
目標調整
調整目標的目的是為了緩解基礎費用的波動性( \Delta b = b_{i+1} - b_i Δ b = b i + 1 − b i )。由於目標代表了持續容量的動態範圍,因此當需求落在此範圍內時,目標會進行調整以維持穩定的費用,從而確保網絡能夠處理不同的使用模式,而不會出現過度的波動。
當前塊的目標可以使用以下等式計算,其中K_t K t表示每單位的調整率:
t_{i+1} = t_i(1 + K_t \times (\Delta b - 0)) t i + 1 = t i ( 1 + K t × ( Δ b − 0 ) )
將此方程轉換為指數形式:
t_n = t_0 \exp(K_t \sum_{i=0}^{n-1} \Delta b) = t_0 \exp(K_t \times (b_n - b_0)) t n = t 0 exp ( Kt∑n − 1i = 0Δb ) = t0exp ( Kt × ( bn − b0 ) )
目標變量具有如下定義的約束:
t_i \in [t_{min}, t_{max}] t i ∈ [ t m i n , t m a x ]
為了方便起見,我們可以將參考基礎費用定義為MIN_TARGET_BLOBS_PER_BLOCK和MAX_TARGET_BLOBS_PER_BLOCK 。每單位價格變動的調整率 ( K_t = \frac{1}{\text{Target Blob Update Fraction}} K t = 1 Target Blob Update Fraction )可以使用以下公式計算:
K_t = \dfrac{\ln{\dfrac{t_\text{max}}{t_\text{min}}}}{b_\text{最大目標} - b_\text{最小目標}} K t = ln最大時間最小時間 b最大目標− b最小目標
數學模型
雙變量 EIP-1559 機制中的具體調整規則僅使用以下公式計算基礎費用和目標費用:
b_n = b_0 \, \exp(K_b \sum_{i=0}^{n-1} g_i - t_i) b n = b 0經驗值( K b ∑ n − 1 i = 0 g i − t i )
t_n = t_0 \exp(K_t \times (b_n - b_0)) t n = t 0 exp ( Kt × ( bn − b0 ) )
該模型的關鍵點是:
- 每當使用的 blob gas 大於或小於目標 blob gas 時,基本費用就會分別向上或向下移動。
- 目標不是一個固定的數字,而是根據當前的基本費用動態變化的。
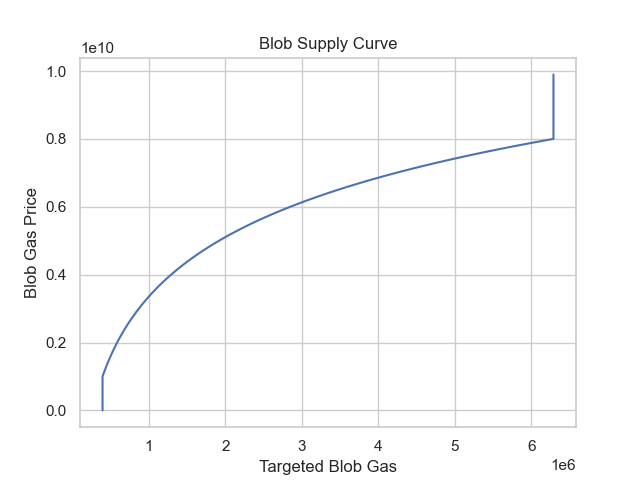
下圖展示了具有供應彈性的供應曲線,其中產能對當前價格做出動態反應,而不是維持固定目標。
參數
該提案中引入的新參數包括:
-
MIN_TARGET_BLOBS_PER_BLOCK -
MAX_TARGET_BLOBS_PER_BLOCK -
MIN_TARGET_BLOB_GAS_PER_BLOCK -
MAX_TARGET_BLOB_GAS_PER_BLOCK -
BASE_FEE_AT_MIN_TARGET_BLOBS -
BASE_FEE_AT_MAX_TARGET_BLOBS -
TARGET_BLOB_UPDATE_FRACTION
仿真分析
為了進行以下模擬分析,這些參數設置如下:
MIN_TARGET_BLOBS_PER_BLOCK = 3 MAX_TARGET_BLOBS_PER_BLOCK = 48 MAX_BLOBS_PER_BLOCK = 72 BASE_FEE_AT_MIN_TARGET_BLOBS = 1_000_000_000 BASE_FEE_AT_MAX_TARGET_BLOBS = 8_000_000_000 GAS_PER_BLOB = 2 ** 17 MIN_TARGET_BLOB_GAS_PER_BLOCK = MIN_TARGET_BLOBS_PER_BLOCK * GAS_PER_BLOBMAX_TARGET_BLOB_GAS_PER_BLOCK = MAX_TARGET_BLOBS_PER_BLOCK * GAS_PER_BLOBMAX_BLOB_GAS_PER_BLOCK = MAX_BLOBS_PER_BLOCK * GAS_PER_BLOBMAX_EXCESS_BLOB_GAS_PER_BLOCK = max (MAX_BLOB_GAS_PER_BLOCK - MIN_TARGET_BLOB_GAS_PER_BLOCK,MAX_BLOB_GAS_PER_BLOCK - MAX_TARGET_BLOB_GAS_PER_BLOCK,MIN_TARGET_BLOB_GAS_PER_BLOCK - 0 ,MAX_TARGET_BLOBS_PER_BLOCK - 0 , 0 )BLOB_BASE_FEE_UPDATE_FRACTION = int (MAX_EXCESS_BLOB_GAS_PER_BLOCK / np.log( 1.125 ))TARGET_BLOB_UPDATE_FRACTION = int ((BASE_FEE_AT_MAX_TARGET_BLOBS - BASE_FEE_AT_MIN_TARGET_BLOBS) / np.log(MAX_TARGET_BLOBS_PER_BLOCK / MIN_TARGET_BLOBS_PER_BLOCK)) 場景 1:Blob 需求低於最低目標
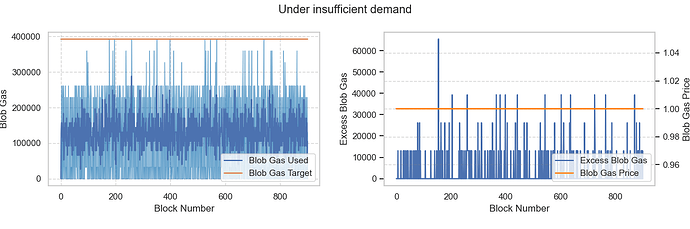
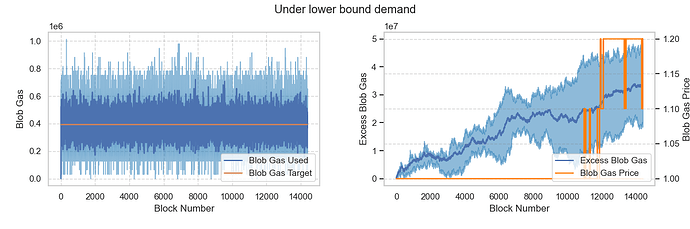
假設平均需求約為 2 個 blob,低於MIN_TARGET_BLOBS_PER_BLOCK ,即供應過剩的情況。結果顯示,基本費用仍保持在MIN_BASE_FEE_PER_BLOB_GAS wei,符合預期。
場景 2:Blob 需求接近最低目標
假設平均需求量約為 3 個 blob,相當於MIN_TARGET_BLOBS_PER_BLOCK 。結果顯示,過剩的 blob gas 開始累積,基礎費用上升至MIN_BASE_FEE_PER_BLOB_GAS以上。
場景 3:Blob 需求介於最小目標和最大目標之間
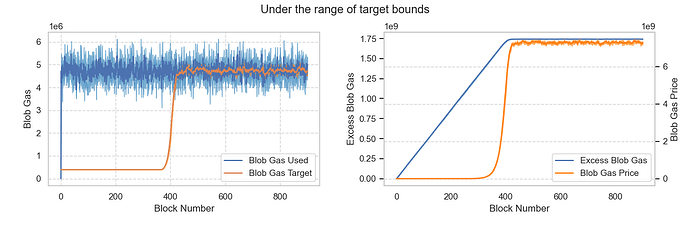
假設平均需求約為 36 個區塊,介於MIN_TARGET_BLOBS_PER_BLOCK和MAX_TARGET_BLOBS_PER_BLOCK之間。結果顯示,目標區塊大約需要 400 個區塊來調整並跟蹤實際需求。當市場達到均衡時,基礎費用保持穩定。
場景 4:Blob 需求接近最大目標
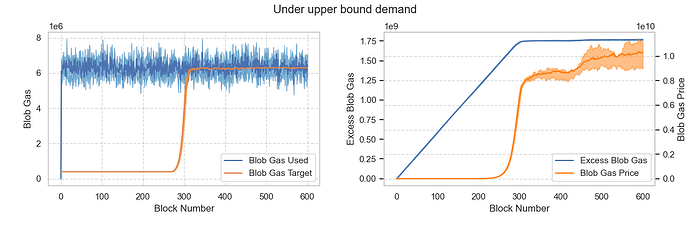
假設平均需求量約為 48 個區塊,相當於MAX_TARGET_BLOBS_PER_BLOCK 。結果顯示,目標區塊需要大約 300 個區塊才能達到MAX_TARGET_BLOBS_PER_BLOCK數量。此後,基礎費用將由 EIP-1559 的原始價格更新函數控制。
場景 5:Blob 需求高於最大目標
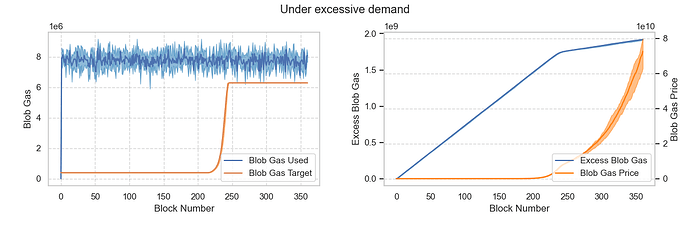
假設平均需求量約為 60 個區塊,超過了MAX_TARGET_BLOBS_PER_BLOCK上限。結果顯示,目標區塊需要 240 個區塊才能達到MAX_TARGET_BLOBS_PER_BLOCK上限。此後,基礎費用將如預期般呈指數級增長。
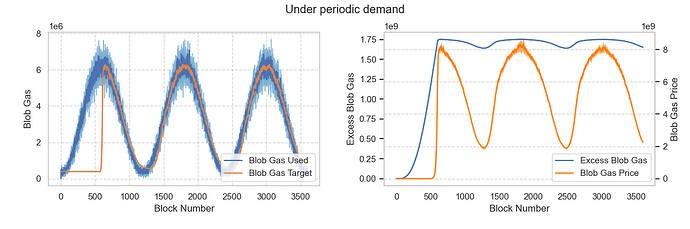
場景 6:Blob 需求定期變化
假設平均需求在[3, 48]範圍內呈週期性變化。結果表明,實際需求上升時,目標blob增加;實際需求下降時,目標blob減少。基礎費用也隨實際需求不斷變化。
費用市場增長生命週期
根據以上結果,我們確定了雙變量 EIP-1559 費用市場的三個階段:
初期階段:實際需求小於或等於MIN_TARGET_BLOBS_PER_BLOCK 。市場缺乏有效的價格信號來合理匹配供需;無論實際使用模式如何,價格始終保持在最低水平。但是,我們可以通過設置相對較低的MIN_TARGET_BLOBS_PER_BLOCK和BASE_FEE_AT_MIN_TARGET_BLOBS值來輕鬆引導市場。
增長階段:實際需求介於MIN_TARGET_BLOBS_PER_BLOCK和MAX_TARGET_BLOBS_PER_BLOCK之間。目標 Blob 和基礎費用均受機制控制,並隨著實際需求穩步變化。隨著 Blob 供應量的擴大,市場不會回到初始階段。
成熟階段:實際需求超過MAX_TARGET_BLOBS_PER_BLOCK 。目標 Blob 達到MAX_TARGET_BLOBS_PER_BLOCK 。基本費用會根據網絡擁堵情況波動。
實證分析
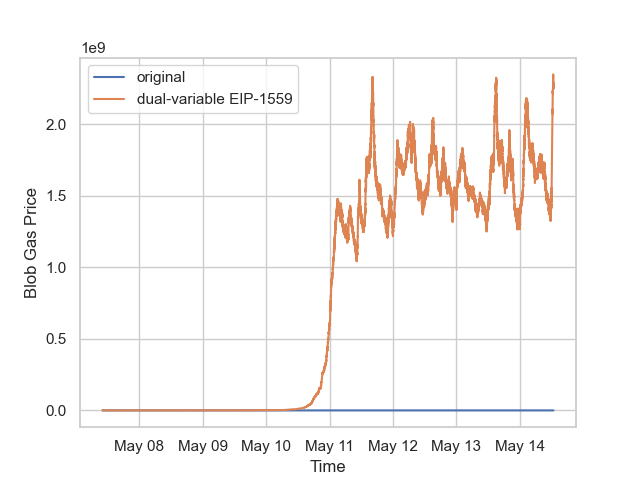
我們使用Blobscan API收集了從區塊 22431084 到 22481502(代表 Pectra 分叉後一週)的區塊數據。
我們可以看到,由於 Blob Gas 使用量低於目標值,Pectra 分叉後 Blob Gas 價格(藍線)迅速跌至 1 wei,表明供應過剩。此後,Blob Gas 價格一直保持在 1 wei, Dune Analytics 的數據也證實了這一點。
當我們使用相同的歷史數據模擬雙變量 EIP-1559 機制時,結果(橙色線)顯示,blob gas 價格大約需要 4 天才能上漲到 1.5 gwei 左右,並且目標 blob 遵循現實世界的 blob 需求來平衡供需。
關於其他 EIP 的一些想法
Blob 容量擴展策略
當前,以太坊數據可用性 (DA) 層的擴展策略是使用僅修改 blob 參數 (BRO) 分叉,它提供了一種輕量級機制,可以通過僅修改 blob 相關參數( target和max )的硬分叉來逐步擴展 blob 容量。與傳統硬分叉相比,BRO 分叉不僅降低了協調的複雜性和風險,還允許 Layer 2 利益相關者參與測試和推進升級。因此,它代表了一種相對高效的迭代擴展解決方案。
然而,這種解決方案也存在一些缺陷。首先,由於供應過剩,每次升級 Blob 容量時,基礎費用仍然會降至 1 wei。這意味著我們必須反覆從零開始增加需求。其次,BRO 分叉仍然是硬分叉,需要人工協調和決策,這會帶來政治衝突和潛在的延遲。
與現有方法相比,雙變量 EIP-1559 為擴展 Blob 容量提供了更有效的解決方案。它使以太坊能夠實時響應 Blob 需求,並在擴展期間穩定 Blob 費用。整個流程無需許可且無需信任地運行。L1 客戶端團隊和 L2 利益相關者可以通過在此機制中設置適當的參數來專注於網絡安全,而市場力量則決定供需之間的最佳平衡。
Gas 限制縮放
近期有消息稱,以太坊計劃將 gas 上限提高至每區塊 4500 萬,這將有可能提高 L1 網絡效率和 L2 吞吐量。
區塊 Gas 限制的擴展可能會面臨與 Blob 擴展相同的供應過剩問題。為了避免這種供應過剩的情況,未來雙變量 EIP-1559 也可以應用於區塊 Gas 限制或任何多維資源。
關於 EIP-7918
EIP-7918建議將 blob 基礎費用與實際執行 gas 成本掛鉤,以確保 blob 交易對區塊使用量做出相應貢獻。
雖然雙變量 EIP-1559 與 EIP-7918 並不衝突,但兩者都試圖解決與 Blob 費用市場有效性相關的類似問題。在我看來,雙變量 EIP-1559 在多維 EIP-1559 路線圖中提供了一個更清晰的解決方案。在 EIP-7918 下,將各種資源費用關聯起來會使定價流程變得複雜。隨著多維 EIP-1559 的推出,資源定價的複雜性將提升幾個數量級,使費用更難預測。當 Blob 需求下降,而執行 Gas 價格卻上漲時,用戶可能會感到困惑。
結論
可以將其想象成一個智能高速公路收費系統。原始的 EIP-1559 僅在交通擁堵時調整收費價格。我們的雙變量系統更加智能:它還可以根據長期交通模式添加或移除收費車道。當交通量持續超出容量時,它會逐步開放更多車道並調整價格。當交通量持續較低時,它會關閉部分車道以維持合理的收費價格。這使得該系統在增長和擴展階段都具有經濟可行性。
未來1-2年內,blob吞吐量將按計劃擴展至48/72,當二維採樣實現後,最大blob數量可能增加到512個。隨著網絡容量的擴展,我們也將解決當前定價系統所依賴的擁堵問題。預計在擴展期間,費用市場將失效。
雙變量 EIP-1559 機制解決了網絡擴容過程中費用市場崩潰的關鍵問題。通過實時自動調整價格和容量,該機制能夠為驗證者提供經濟激勵,為用戶提供可預測的成本,並在整個擴容階段確保網絡安全。最重要的是,該解決方案易於實施,因為它在現有 EIP-1559 的基礎上進行了少量改動。無論市場需求是快速增長還是下降,費用市場都能保持強勁有效。