作者:Nicolas Vescovo
“BitVM” 這一框架的設計目的是將任意鏈外計算的樂觀主義驗證(optimistic verification)帶給比特幣網絡,從而允許更加複雜的操作,比如 “zk rollup” 和側鏈橋。BitVM 通過引入支持樂觀主義驗證的機制,增強了比特幣的靈活。“BitVMX” 則使用不同的技術,讓部分操作能夠更快、更高效地檢查,取得了更好的成果。在這一語境下,“樂觀主義驗證” 表示基於一種假設的驗證方法 —— 假設操作都是有效的,除非能證明不是。
為了保證這樣的系統的安全性,BitVM 和 BitVMX 使用 Lamport 簽名和 Winternitz 簽名。這些密碼學方法是確保整個過程具有 “富狀態性(statefulness)” 的關鍵。通過使用這些簽名方案,BitVM 和 BitVMX 提供了強大的安全性,可以抵禦多種攻擊並保證所有操作都得到了正確執行。
本文解釋了 “Lamport 簽名” 和 “Winternitz 簽名” 分別是什麼樣的、後者如何延申了前者的概念,以及它們如何用在 BitVM 中。我們也將解釋,這些簽名如何在 BitVM 和 BitVMX 中帶來富狀態性、確保特定的變量一旦被設定,在後續的腳本中就無法再修改和複用。
理解 Lamport 簽名和 Winternitz 簽名
一種電子簽名方案就是一種用來驗證電子消息(或者說文檔)的真實性和完整性的數學方案。簡單來說:
- Lamport 簽名使用了一次性的電子承諾(基本上基於哈希函數)來提供不可偽造的簽名。
- Winternitz 簽名則利用一種單向函數的多輪迭代(通常會形成鏈條)來實現密碼學安全性。
Lamport 簽名:由 Leslie Lamport 在 1970 年代晚期提出,是一種基於哈希函數的電子簽名方案。它利用密碼學哈希函數的單向特性來獲得安全性。Lamport 簽名因其簡潔性以及抵禦量子計算攻擊的能力而聞名。它的模式是預先生成大量的密鑰對,然後用它來簽名。不過,其巨大的簽名體積,也可能會限制其應用。
Winternitz 簽名:由 Ralph Merkle 和 Robert Winternitz 分別獨立提出,是另一種基於哈希函數的電子簽名。它提供了跟 Lamport 簽名相似的安全性,且更加高效。相比 Lamport 簽名,Winternitz 簽名利用了一種鏈條結構,降低了簽名的大小,這使它更加實用。通過允許用戶調整 Winternitz 參數,這些簽名可以在計算速度和簽名體積之間取得平衡,實質上,是將 Lamport 簽名方案一般化了。
Lamport 簽名:形式化視角
在本章中,我們提供了對 Lamport 簽名如何生成、使用和驗證的分步驟解釋。我們探索了密鑰生成過程、消息簽名和簽名驗證的技術方面。最後,我們討論了與之有關的安全性考慮和弱點。
密鑰生成
為需要簽名的消息中的每一個比特 i 生成兩串隨機的字符串(比特序列),分別記為 $S_{i, 0}$ 和 $S_{i, 1}$ 。如果消息的長度是 n 比特,那麼 i 的取值範圍是從 0 到 $n-1$ 。
私鑰就是由這些隨機字符串對 $(S_{i, 0}, S_{i, 1})$ 組成的(其中 $i = 0, 1, …, n-1$)。
對於私鑰中的每一對字符串 $(S_{i, 0}, S_{i, 1})$ ,計算這些字符串的哈希值並保持配對:$(H(S_{i, 0}), H(S_{i, 1}))$ 。
公鑰則是由這些哈希值對 $(H(S_{i, 0}), H(S_{i, 1}))$ 組成的(其中 $i = 0, 1, …, n-1$)。
簽名消息
將待簽名的消息 m 轉化為二進制形式,即 $m = m_0m_1…m_{n-1}$ ,每一個 $m_i$ 都是一個比特(其值為 0 或 1 )。
對於消息的每一個比特 $m_i$ ,在簽名中包含對應的私鑰 $S_{i, m_i}$ 。
最終,簽名就是一個有 n 個元素的序列:(S_{0, m_0}, S_{1, m_1},...,S_{{n-1}, m_{n-1}})。
驗證一個簽名
給定一條消息 m 及其簽名 (S_{0, m_0}, S_{1, m_1},...,S_{{n-1}, m_{n-1}}) 。
將消息 m 轉化為二進制形式:$m = m_0m_1…m_{n-1}$ 。
對於每一個比特 $m_i$ ,計算簽名中對應元素的哈希值:$H(S_{i, m_i})$ 。
驗證計算出來的每一個哈希值 $H(S_{i, m_i})$ 都跟公鑰中的對應元素($H(S_{i,0})$ 或 $H(S_{i, 1})$)相匹配。
安全考慮
- 一次性使用:僅在每一對密鑰只用來簽名一條消息時,Lamport 簽名方案才是安全的。使用同一對密鑰來簽名多條消息會揭曉部分私鑰,從而犧牲安全性。
- 哈希函數:Lamport 簽名方案的安全性依賴於所用的密碼學哈希函數的強度 —— 它應該能抵抗原像攻擊、第二原像攻擊以及碰撞攻擊。
為什麼它們叫 “一次性簽名”?
Lamport 簽名方案被稱作 “一次性簽名”,因為在這種方案中,一旦同一把公鑰用來簽名多於一條消息,其安全性就會急劇下降。其中的道理在於,每多簽名一條消息,就會多揭曉一些關於私鑰的信息,從而讓攻擊者更容易偽造簽名。
在觀察到一個簽名之後,攻擊者就知道了公鑰中的每一對哈希值中的一個的原像。然而,有了兩個簽名,攻擊者就能知道其中一半哈希值對的兩個原像,以及另一半哈希值對的一個原像。有了三個簽名,攻擊者就能知道其中四分之三的哈希值對的兩個原像;以此類推。這種逐步的曝光,意味著同一個公鑰每多籤一個名,其安全性實質上都會減半。
(譯者注:作者在上一段的推理中使用了消息的比特隨機分佈的假設。)
舉個例子,如果一個公鑰被設計成對第二原像攻擊提供 256 比特的安全性以及對碰撞攻擊提供 128 比特的安全性,在它簽名三次之後,實用的攻擊就有可能發動。在它簽名四次之後,找出 消息-簽名 的配對就變得非常簡單了。因為攻擊者可以使用已知的哈希值(及其原像)來為自己選定的消息構造新的有效簽名,漏洞由此產生;在消息有一些靈活性的語境中尤其如此。
在使用超過一次時 Lamport 簽名的漏洞
Lamport 簽名在同一公鑰重複簽名時的主要漏洞在於,攻擊者能夠利用從以往觀察到的簽名中獲得的信息,為任意消息偽造簽名。假設一個攻擊者能夠知曉使用同一個公鑰為多條消息生成的簽名。這時候,TA 就能將已知的簽名拼湊在一起,構造出新的有效簽名。
比如說,考慮一個消息長度為 16 比特的情形:
簽過名的消息有:m1 = 0001111101110001 以及 m2 = 0111110000111111 。攻擊者就能為一條新消息 m* = 0101111000110101 偽造簽名,只需要將對上述兩條消息的簽名中的對應部分拼湊起來。但凡是使用從 m1 和 m2 的對應位置的比特構造出的 m* ,就都能偽造出有效的簽名 —— 只需要對應於這些比特的值的哈希值的原像,就能構造出簽名。
如果消息在簽名之前哈希過(也即簽名的不是消息本身,而是消息的哈希值),那麼攻擊就要變得更加複雜,但依然是可行的。攻擊者必須找出一條消息 m* ,其哈希值與以往簽過名的消息的哈希值有足夠多相同的部分。每多一條可以觀察到的簽名,都可以減少攻擊所需的哈希函數求值的次數,也就是讓偽造變得更加容易。
本質上,在使用 Lamport 簽名方案時,為了保持安全性,每個公鑰都只應使用一次。為多條消息的簽名重複使用一個公鑰,將允許攻擊者獲得足夠多的信息來偽造新的簽名,最終打破這種密碼系統的完整性。
Winternitz 簽名:理論視角
如我們已經介紹過的,Winternitz 一次性簽名(WOTS)是 Lamport 簽名的一種強化,極大地縮小了簽名和公鑰的體積。但天下可沒有免費的午餐。這種提升的代價是,生成和驗證簽名都要更花功夫。在本章中,我們會提供一種形式化的定義,並解釋 Winternitz 簽名是如何工作的。
參數與啟動
- W:Winternitz 參數,一個正整數,決定一次能處理的比特數量。
- n:哈希輸出的長度(以比特計)。
- l:消息摘要的分段數量,計算方式是 $l = \lceil n/W \rceil$ 。這裡的 $\lceil \rceil$ 意味著取大於或等於給定數字的最小整數 。
- l’:校驗和的長度,計算方式是 $l’ = \lceil (\log_2(l * (2^W - 1)))/W \rceil$
- L:簽名的總長度,L = l + l’ 。
密鑰生成
生成 L 個長度為 n 的隨機比特串 $S_i$ ,其中 $i = 0, 1, …, L-1$ 。
私鑰就是由這些隨機比特串組成的:$S = (S_0, S_1, …, S_{L-1})$ 。
對於每一個私鑰碎片 $S_i$ ,連續應用哈希函數 $2^W$ 次:$P_i = H^{2^W}(S_i)$ 。
公鑰就是用這些哈希結果組成的:$P = (P_0, P_1, …, P_{L-1})$
簽名消息
將待簽名的消息 m 分割為長為 W 比特的 l 個碎片:$m = (m_0, m_1, …, m_{l-1})$ 。
計算校驗和 C :$C = \sum_{i=0}^{l-1}(2^W - 1 - m_i)$ 。
將校驗和 C 轉化為長為 W 比特的 l’ 個碎片:$C = (c_0, c_1, …, c_{l’-1})$ 。一般來說,會把第一個元素當成校驗和:$C = (c_0)$ 。
對於摘要的每一個碎片 $m_i$ 以及校驗和 $c_i$ ,通過哈希對應的私鑰碎片 $m_i$ 次來生成簽名 $\sigma_i$ :$\sigma_i = H^{m_i}(S_i)$ ,其中 $i = 0, 1, …, l-1$ 。
類似的,對於校驗和的部分:$\sigma_{l+j} = H^{c_j}(S_{l+j})$ ,其中 $j = 0, 1, …, l’-1$ 。
完整的簽名就是這些碎片的拼接:$\sigma = (\sigma_0, \sigma_1, …, \sigma_{L-1})$ 。
驗證簽名
給定消息 m 及其簽名$\sigma = (\sigma_0, \sigma_1, …, \sigma_{L-1})$ 。
將消息 m 分割成 l 份:$m = (m_0, m_1, …, m_{l-1})$ 。
計算校驗和 C 並將它分割成 l’ 份:$C = (c_0, c_1, …, c_{l’-1})$ 。
對於每一個簽名碎片 $\sigma_i$ ,應用哈希函數 $2^W - 1 - m_i$ 次,期待它能推導出公鑰碎片:
$$
P_i : \widehat{P_i} = H^{2^W - 1 - m_i}(\sigma_1) , \qquad i = 0, 1, …, l -1
$$
類似地,對於校驗和的部分:
$$
\widehat{P_{l+j}} = H^{2^W - 1 - c_{j}}(\sigma_{l+j}) , \qquad j = 0, 1, …, l’ -1
$$
如果派生出來的公鑰 $(\widehat{P_0}, \widehat{P_1},…, \widehat{P_{L-1}})$ 與公鑰 $P = (P_0, P_1, …, P_{L-1})$ 相匹配,則說明這是個有效的簽名。
安全考慮
- 參數挑選:W 的選擇會影響簽名體積與計算效率的取捨。更大的 W 值會降低簽名的體積,但會提高簽名和驗證的計算負擔。
- 一次性使用:與 Lamport 簽名一樣,Winternitz 簽名也是一次性使用的。在多條消息的簽名中重複使用同一對密鑰,會因為揭曉關於私鑰的信息而犧牲安全性。
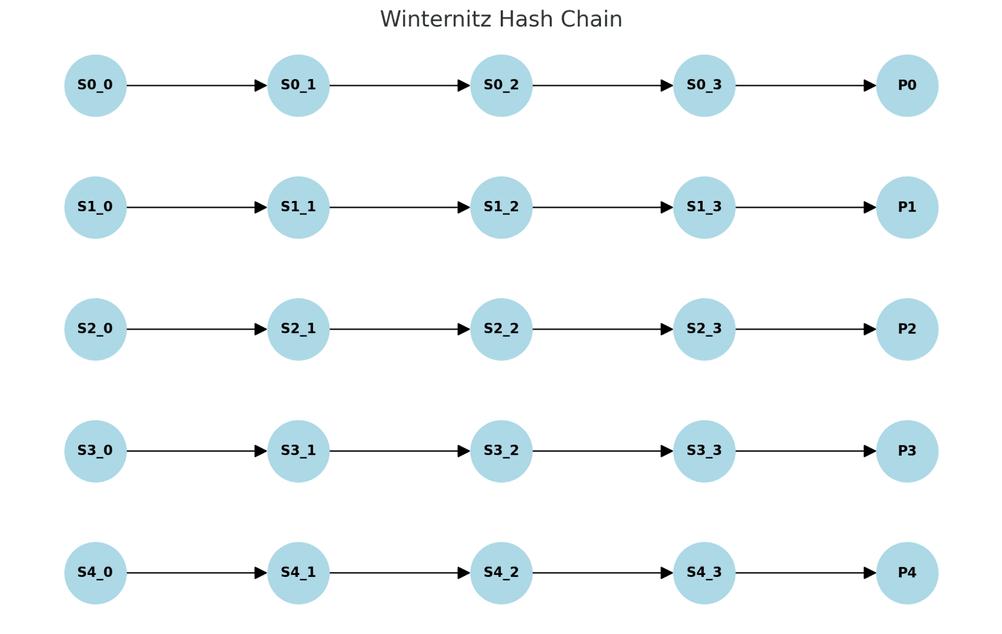
下圖演示了當 W = 2 ,l = 5 時,Winternitz 鏈條的序列(從私鑰派生公鑰)。每一個箭頭都表示一次哈希求職。(譯者注:此處原文有誤,已糾正。)
為什麼校驗和是必要的?
從技術角度看,Winternitz 簽名方案中的校驗和,對於保持安全性和保證簽名過程的完整性,都是必要的。
Winternitz 簽名方案的模式是將消息分割成碎片,然後根據各碎片的值將對應的私鑰碎片哈希一定的次數(譯者注:此處原文有誤,已糾正)。然而,這個過程就帶來了一個漏洞:只要攻擊者知道一個簽名(它由各哈希鏈條上的某個值組成),就可以使用哈希鏈條上的後續元素來構造有效的簽名。這是因為,只要揭曉了哈希鏈條上的一個成員,攻擊者就可以計算出所有後續的哈希值(它們本身就是同一私鑰碎片對某個值的簽名),從而打破簽名的完整性。
為了消除這種風險,檢驗和就是關鍵了。它保證了,對消息的任何改動,都會讓校驗和也發生對應的、一致的改動,而這種計算,在沒有私鑰的情況下是計算上不可行的。因為,想要使用一些哈希鏈條上的後續的值,將需要知道簽名校驗和的哈希鏈條上比較靠前的值(在沒有私鑰的情況下,這是不可能做到的)。校驗和是一個額外的驗證層,讓沒有原像攻擊能力的攻擊者無法在不知道私鑰的情況下為另一條消息生成一個有效的簽名。
(譯者注:此處的推理是,由於哈希鏈條是單向的,所以,在不考慮校驗和的情況下,知曉一條 WOTS 簽名只允許攻擊者為數值更大的各個 $m_i$ 偽造簽名,也即使用哈希鏈條上更靠後的值。然而,在使用前述校驗和 $C = \sum_{i=0}^{l-1}(2^W - 1 - m_i)$ 的情況下,更大的 $m_i$ 將帶來更小的 C,簽名這樣的 C 將要求使用私鑰哈希鏈條上更為靠前的值,想要從已知的簽名中推導出它意味著逆轉哈希運算,這是計算上不可行的。因此,如無私鑰,就無法制作出簽名。)
此外,校驗和也保證了簽名過程的完整性。它是一個最終的檢查,驗證在簽名過程中沒有遺漏或替換某個比特。這保證了整條消息都被考慮到了、在簽名中有了正確的表示。
此外,校驗和還驗證了簽名的整體完整性。也就是說,應用了正確的哈希迭代次數,從而保證簽名既準確又安全。
沒有校驗和,這種方案是很容易被攻擊的。攻擊者可以很容易替換掉消息碎片,並在沒有私鑰的情況下創建出有效的簽名。缺乏校驗和也可能導致不完整驗證,讓替換或截短的消息也被當成是簽過名的。
BitVM 和 BitVMX:Lamport 簽名和 Winternitz 簽名閃耀的地方
我們已經提到,BitVM 和 BitVMX 是為了將任意鏈外計算的樂觀驗證帶給比特幣網絡而設計的框架。兩者都能使用 Lamport 簽名或 Winternitz 簽名來創建健壯的數據承諾。在這個語境下,一個承諾是特定的一段數據在某個時間點已經存在、被安全記錄、且簽過名的密碼學保證。這些承諾可以在未來驗證者的挑戰中被引用。這些簽名的使用,保證了每一個承諾都是可以驗證並且抗篡改的。
如果驗證者同意操作者,那就不需要做什麼,操作就會正常處理;但如果驗證者不同意操作者,因為雙方都曾公開簽名這些承諾,所以協議允許雙方使用對方的信息來證明對方嘗試欺詐或正在執行錯誤的操作。
BitVM 帶來的一項關鍵創新是能夠跨越多筆交易而保持和引用狀態。這是通過使用一次性簽名來承諾每一步驟時刻的狀態來實現的。通過利用 Lamport 簽名,BitVM 保證了每一次狀態轉換都得到了安全的承諾,並且可以在後續操作中可靠地引用。
結論
Lamport 簽名和 Winternitz 簽名有一系列好的屬性,使它們適合在 BitVM 和 BitVMX 中使用。它們集成到這些協議中,極大地加強了比特幣的腳本編程能力,帶來了高效且安全的富狀態操作。它們在數據承諾中的用法,保證了網絡可以處理更加複雜的交易但保持安全性和性能。這些密碼學技術,是比特幣未來的關鍵,因為它們為更加高級和安全的去中心化應用(比如信任最小化的側鏈橋、樂觀驗證的零知識證據)鋪平了道路。
(完)







