前言
在上一部分中,我們基本上了解了zk-SNARK 背後的數學和編碼基礎。現在我將繼續深入研究更新且相當複雜的概念,以便您可以更深入地瞭解zk-SNARK背後的技術!
算術電路(算術電路)
運算電路的概念
該運算電路是一個有向無環圖(DAG) ,或者簡單地說,它是一個有向無環圖,包括:
- 這些節點Vai加法門和乘法門。
- 邊代表導體,建立在有限場Fp 上。一根電線將一個端口的輸出連接到另一個端口的輸入。每個端口有兩個輸入和一個輸出。
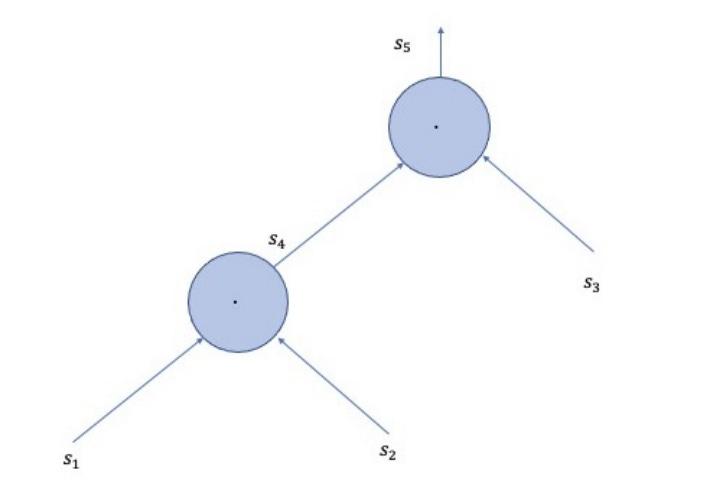
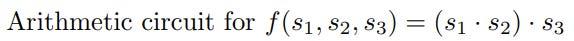
算術電路以最終輸出結束。上圖展示了一個算術電路的示例,我們可以看到數據如何被處理並通過每個門以製作最終結果。
算術電路告訴我們zk-SNARK如何處理和證明計算,而不透露任何信息。算術電路可以用圖表來描述,其中包含系統排序的算術運算。
算術電路的運算
考慮上圖,算術電路允許我們計算
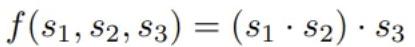
看上圖,我們看到這個過程從第一個內核門開始,它接收s1和s2作為輸入,並製作s4作為輸出。接下來, s4和s3被輸入到第二個內核門以製作最終輸出s5 。
對於m端口、 n線電路,我們將能夠確定
見證人 s = (s1, s2, s3,…, sn)
分配給電路的n條線,使得每個門的輸入和輸出滿足由門的操作確定的約束。
一個m端口、 n線運算電路確定證人之間的關係
s = (s1, s2, …, sn)
這樣對於一個常數

然後
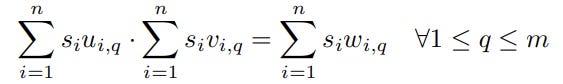
上述約束屬於m個rank-1約束的集合,其目的是模擬算術電路中乘法門的輸入和輸出之間的關係。
特定的1 級約束的一個例子是 Eq
s1 。 s2 – s3 = 0。
該方程描述了電路中的乘法器門,它採用兩個輸入s1和s2 ,然後產生輸出s3 。因此, s1和s2的乘積必須等於s3才能滿足方程。
像這樣的一組 m階 1約束可以推廣為二次算術程序。
QAP是將算術電路轉換和下降為更容易驗證操作而無需重新渲染整個電路的形式的工具。
二次算術程序
zk-SNARK的核心在於二次算術程序(QAP )。 QAP可以代表任何算術電路,包括加法門和乘法門。基於QAP,證明器可以製作他知道輸入值,而無需透露有關該值或程序內部行為的任何信息。
zk-SNARK研究員Eran Tromer從基本數學原理出發,得出了zk-SNARK構建流程如下:

上面的步驟可以Chia兩半。在本文中,將深入解釋該過程的“前半部分” 。該過程的“前半部分”可以認為是從“計算”到“QAP”的步驟,這是將初始計算轉換為可用於建立zk-SNARK 的數學形式的部分。
我將用最容易理解的方式解釋如下:
在我們可以使用zk-SNARK解決任何計算問題之前,我們必須將問題轉換為合適的“形式” 。這種形式稱為QAP ,即“二次算術程序”。
一旦我們將問題轉換為QAP ,我們將繼續使用一些特定的輸入來解決它。找到的解決方案稱為“證詞”。這就像我們解決完一個謎題並知道答案一樣。
現在我們有了答案,我們需要製作一種方法來證明我們知道答案而不透露答案。這個過程製作了一個“非洩露證據”,這意味著它允許我們證明我們知道答案,而不必說出來。
最後,其他人可以使用單獨的過程來檢查我們製作的證據,以確認我們確實知道答案,而不知道答案實際上是什麼!
例如:我們有以下等式:
x**3 + x + 5 == 37 (建議答案為 3)
我們將通過編寫一個簡單的計算機程序來證明我們知道上述數學方程的解,而不必揭示解,如下所示:

qevel函數將計算方程x**3 + x + 5的值。當我們將數字 3 代入 x 時,函數將返回 35,這就是我們想要的結果。
然而,在這種情況下我們會看到編程語言的侷限性。該語言僅支持基本算術運算(+、-、*、/)和固定指數的冪(x**7,而不是 x**y) 。它不支持餘Chia(%)或比較(>、<、≤、≥) ,因為在有限循環群算術中沒有直接執行取模或比較的有效方法。
這裡的解決方案是我們可以擴展該語言以支持其他操作,例如餘數Chia和比較
例如:
如果 x < 5:y = 7;否則:y = 9
將它們轉換為算術:
y = 7 * (x < 5) + 9 * (x >= 5)
您可以參考一個編譯器,該編譯器可用於將代碼轉換為vbuterin實現的zk-SNARK可用的形式(僅用於教育目的;尚未準備好在實踐中為zk-SNARK創建QAP )
扁平化
轉換為這種形式的QAP的第一步是“扁平化”步驟,簡單來說,這是對編程代碼進行改造以使其更簡單的步驟,每行只執行一個基本操作。
在上面的示例中,初始計算機程序具有複雜的數學表達式。 “展平”的過程將這個表達式分成小部分,每個部分只做一個簡單的計算:
sym_1 = x * x
將x與其自身相乘以製作一箇中間值,稱為sym_1
y = sym_1 * x
然後將中間值sym_1次乘以x以製作y ,遵循精確計算x^3
sym_2 = y + x
添加剛剛用x計算出的y
〜輸出 = sym_2 + 5
最後將sym_2加 5 得到最終結果,並在out前加一個~表示這是程序的最終結果。
非常容易理解!這種“扁平化”過程有助於準備要由zk-SNARK處理的代碼,因為zk-SNARK要求編程代碼採用簡單的形式,可以輕鬆轉換為它可以使用的數學形式。
通往 R1CS 的大門
接下來,我們將進行一系列的計算,將它們轉換成稍微複雜一點的形式,稱為(rank-1約束系統) ,縮寫為R1CS。
R1CS是由三個向量(a, b, c)組成的組的鏈, R1CS 的解是向量s,其中s必須滿足以下方程:
s。作為 。 b – s 。 c = 0
這將檢查輸出值是否是兩個輸入值的正確乘積。如果滿足所有這些條件,我們就有了系統的精確解向量。
我們可以看下圖來更好地理解R1CS :
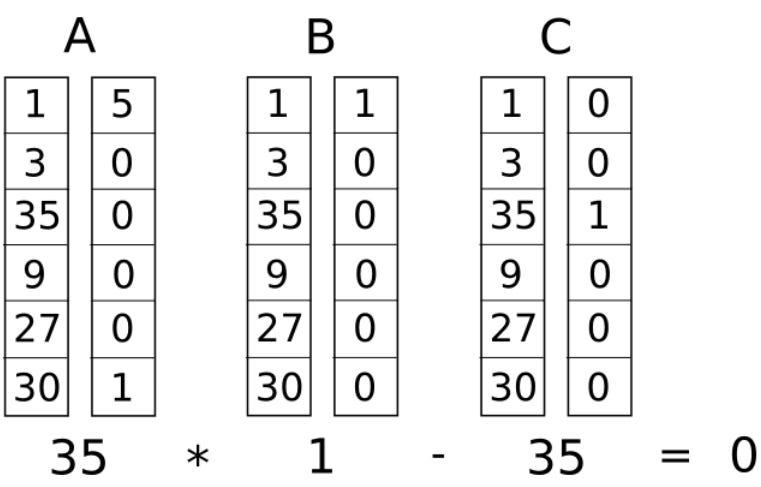
首先,我們將定義系統中使用的變量,我將提供映射變量的步驟如下:
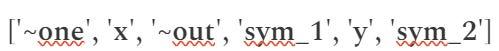
- “~one” (第一個下標代表數字1)
- “x” (輸入變量)
- “~out” (輸出變量)
- “sym_1”、“y”、“sym_2” (中間變量)
向量“s”將包含所有這些變量的值,按照定義的順序。
#我們將給出第一個門的三元組(a,b,c) (對於x * x乘法):

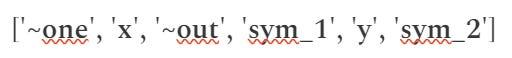
- 向量a和b都包含值[0, 1, 0, 0, 0, 0] 。每個向量中第二個位置的數字 1 表示將在計算中使用變量x的值。具體來說,該值與其自身相乘,因為a和b都將權重放在位置x處
- 向量c的值為[0, 0, 0, 1, 0, 0] ,第四位為數字 1,表示根據a和b計算出的值將與向量s中的變量sym_1進行比較
a = [0, 1, 0, 0, 0, 0] :指定變量“ x ”參與計算。
b = [0, 1, 0, 0, 0, 0] :再次指定“ x ”將與其自身相乘。
c = [0, 0, 0, 1, 0, 0] :結果將存儲在變量“ sym_1 ”中
當“ x = 3 ”時,計算結果為“ 3 * 3 = 9” ,滿足約束“sym_1 = x * x”
#接下來是第二個門(用於乘法sym_1 * x ):

相似的,
a = [0, 0, 0, 1, 0, 0] :指定“ sym_1 ”(如果“x = 3”則為 9 )
b = [0, 1, 0, 0, 0, 0] :指定“ x ”(如果“x = 3”則為 3 )
c = [0, 0, 0, 0, 1, 0] :結果將保存在“ y ”中
計算結果為“ 9 * 3 = 27 ”,滿足約束條件
#接下來是第三個門(用於x + y 加法)

相似的,
a = [0, 1, 0, 0, 1, 0] :指定“x”和“y”
b = [1, 0, 0, 0, 0, 0] :使用值“1” (代表“~one” )以便正確執行加法。
c = [0, 0, 0, 0, 0, 1] : 結果保存到“sym_2”
計算結果為“3 + 27 = 30” ,滿足約束“sym_2 = x + y”
#最後是第四個門(用於加法sym_2 + 5 ):

相似的,
a = [5, 0, 0, 0, 0, 1] :使用“~one”中的值“ 5 ”和“sym_2”中的值“ 1 ”
b = [1, 0, 0, 0, 0, 0] :再次“ ~one” ,以便正確執行加法。
c = [0, 0, 1, 0, 0, 0] : 結果保存到“ ~out”
計算結果為“30 + (5*1) = 35” ,滿足約束條件“~out = sym_2 + 5”
三列A、B和C對應於向量“ a” 、“ b”和“c ”。 C列底部的數字“ 35 ”是最終結果( “~out”)
比較(s . a) * (s . b)和(s . c),它們必須相等(它們的差必須為 0)
此時,向量“s”將包含以下值:
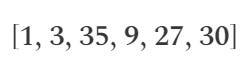
- 1:這是虛擬變量~one的值,它始終為 1 來表示常量 1。
- 3:這是輸入變量x的值。
- 35:這是期望的值,程序的最終結果(變量~out) 。
- 9: x * x的結果,存儲在sym_1中。
- 27: sym_1 * x的結果,存儲在y中。
- 30: y + x的結果,存儲在sym_2中。
最後,完整的R1CS拼湊起來如下圖:

R1CS 至 QAP
下一步是採用此R1CS並將其轉換為QAP 形式,但不是像R1CS那樣使用向量和點積

QAP使用“多項式”,因為它們具有特殊的數學屬性,可以使測試過程變得更容易。
拉格朗日插值是一種繪製經過一系列已知點的曲線(多項式)的方法。如果您有特定數量的點並且想要一條接觸所有這些點的曲線(多項式) ,拉格朗日插值將幫助您找到該曲線。
例如:假設我們想要一個經過(1, 3)、(2, 2)和(3, 4) 的多項式。我們首先創建一個通過(1, 3)、(2, 0)和(3, 0) 的多項式。
一種簡單的方法是取(x-2)和(x-3)的乘積。該函數將具有曲線形狀,在 x=1 處上升並在x=2和x=3處切割水平軸。
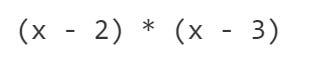
如下:
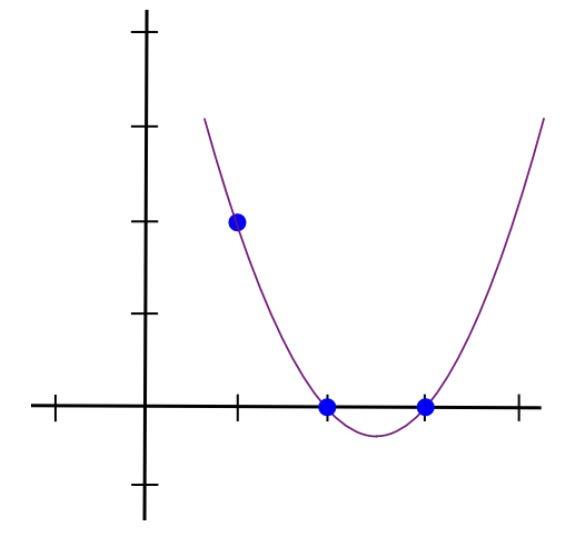
現在,我們只需要“調整”它,使x=1處的高度正確:
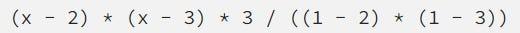
這使得多項式和圖形將顯示如下:

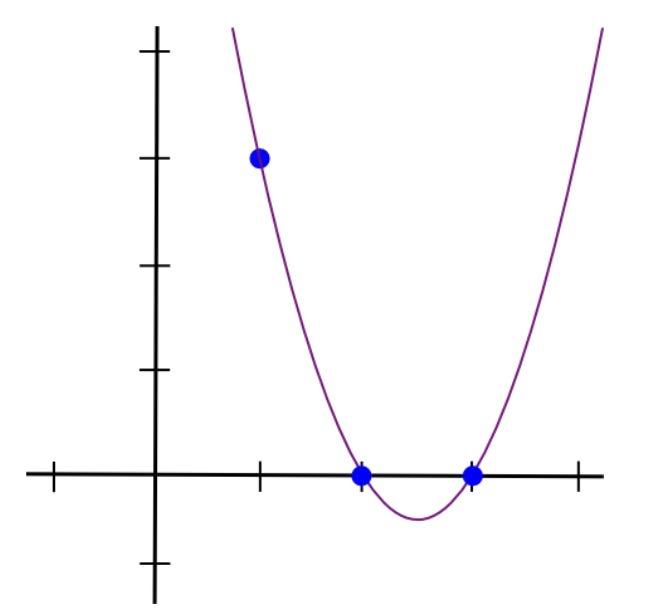
然後我們對剩下的兩個點做同樣的事情,得到另外兩個多項式,將三個多項式加在一起得到:


原始算法需要O(n^3)時間來計算,因為每個n點都需要O(n^2)來乘以多項式。然而,通過更聰明的思考,我們可以將這個時間下降到O(n^2) 。
應用FFT變換等算法,我們可以更快地下降計算時間,這對於具有數千個門的zk-SNARK等應用非常重要。
我們將應用拉格朗日插值來變換R1CS ,方法是獲取每個向量 a的第一個值,然後使用此插值為每個向量創建一個多項式,以便在索引特定數字處評估多項式時,我們得到第一個值對應的向量。
對向量b和c的第一個值執行相同的操作,然後次將此方法應用於每個向量的下一個元素。
我們將得到如下結果:

該算法使用一系列上漲係數來製作多項式:
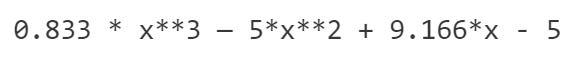
該多項式是正在考慮的QAP(二次算術程序)版本的參數的一部分。
需要注意的是,對於每個使用zk-SNARK驗證的功能,這些參數只需要設置次;一旦設置完畢,它們就可以重複使用。
當評估x=1處的所有多項式時,過程非常簡單,因為您只需將所有係數相加(因為對於k的所有值,1^k始終為1 ),我們將得到以下結果:

- 當多項式 A 在 x = 1評估時,除第二個結果為 1 外,所有結果均為 0
- 當在 x = 1評估多項式 B 時,除第二個結果為 1 外,所有結果也均為 0。
- 當多項式 C 在 x = 1評估時,所有結果均為 0,除了第四個結果為 1。
我們看到這裡的向量三元組(a,b,c)與我們上面創建的第一個邏輯門完全相同。
文章來源: Team Tech/Research AlphaTrue
參考來源:
- 陳 T.、盧 H.、Kunpittaya, T. 和羅 A. (2022)。 zk-snarks 的評論。 arXiv 預印本 arXiv:2202.06877 。 https://arxiv.org/pdf/2202.06877.pdf
- https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649
- https://eprint.iacr.org/2012/215.pd