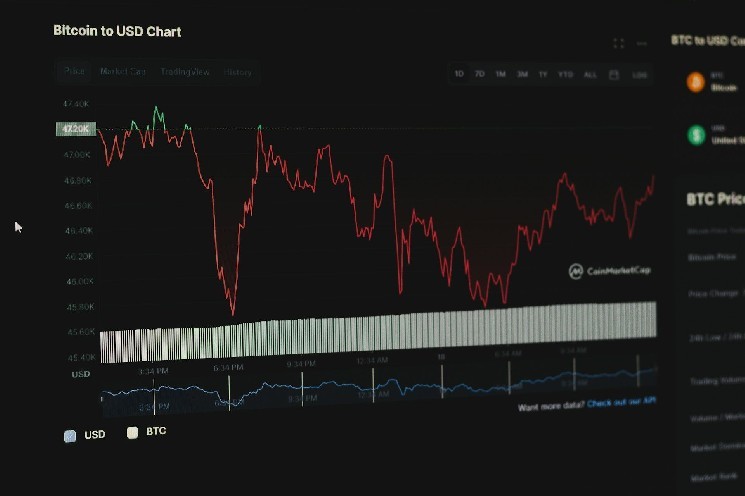
Last month, GPT-4o's image generation function became popular, sparking widespread discussions represented by the Ghibli style, and the craze for generative AI once again swept the Internet.
Behind this wave, latent space, as the core driving force of generative models, has ignited infinite imagination in image and video creation.
Well-known researcher Andrej Karpathy recently forwarded a blog post from Google DeepMind research scientist Sander Dielman, which explored how generative models (such as image, audio, and video generation models) can improve generation efficiency and quality by leveraging latent spaces.
Blog link: https://sander.ai/2025/04/15/latents.html
Since joining DeepMind in 2015, Sander Dielman has participated in multiple projects including WaveNet, AlphaGo, Imagen 3 and Veo, covering deep learning, generative models and representation learning.
In this article, he likens latent variables to the "essence of data" - generating images, speech, etc. by compressing complex information. He also deeply compares variational autoencoders (VAEs), generative adversarial networks (GANs), and diffusion models, showing how latent variables support these models to generate realistic content.
For example, WaveNet, which Dielman helped develop, successfully achieved high-quality speech synthesis using latent variables and has been widely used in multiple Google products. He also used VQ-VAE as an example to illustrate how discrete latent spaces can improve the efficiency of image generation.
This article combines theoretical depth and intuitive insights, and is suitable for readers who are interested in generative models to study in depth.
formula
Training a generative model in a latent space is usually divided into two stages:
1. Train the autoencoder with the input signal. The autoencoder is a neural network that consists of two subnetworks: encoder and decoder. The encoder maps the input signal to the corresponding latent representation (encoding), and the decoder maps the latent representation back to the input domain (decoding).
2. Train the generative model on the latent representation. This step involves using the encoder in the first stage to extract the latent representation of the training data, and then directly training the generative model on these latent representations. The current mainstream generative models are usually autoregressive models or diffusion models.
Once the autoencoder is trained in the first stage, its parameters will not change in the second stage: the gradients of the second stage of the learning process will not be back-propagated to the encoder. In other words, in the second stage, the encoder's parameters are frozen.
Note that the decoder part of the autoencoder does not come into play during the second phase of training, but it is needed when sampling from the generative model, as this will generate outputs in the latent space. The decoder allows us to map the generated latent vectors back to the original input space.
Below is a diagram illustrating this two-stage training approach. Nets whose parameters are learned in the corresponding stage are marked with a "∇" symbol, as this is almost always done using gradient-based learning methods. Nets whose parameters are frozen are marked with a snowflake symbol.
Training method for latent generative models: two-stage training.
There are several different loss functions involved in the two training phases, which are highlighted in red in the figure:
To ensure that the encoder and decoder can convert the input representation to the latent vector and back again with high fidelity, multiple loss functions are used to constrain the relationship between the reconstruction (decoder output) and the input. These usually include simple regression loss, perceptual loss, and adversarial loss.
To limit the capacity of the latent vectors, an additional loss function is often applied directly to them during training, although not always. We call this the bottleneck loss because the latent representation forms a bottleneck in the autoencoder network.
In the second stage, the generative model is trained using its own loss function, separate from the loss function used in stage 1. This is typically the negative log-likelihood loss (for autoregressive models) or the diffusion loss.
Looking deeper into the reconstruction-based loss functions, we have the following:
Regression loss: Sometimes measured as mean absolute error (MAE) in input space (e.g. pixel space), but more commonly as mean squared error (MSE).
Perceptual losses: come in many forms, but typically leverage another frozen pre-trained neural network to extract perceptual features. This loss function encourages a match between these features between the reconstruction and the input, thus better preserving high-frequency content that regression losses mostly ignore. For image processing, LPIPS is a popular choice.
Adversarial loss: Use a discriminator network trained in conjunction with the autoencoder, similar to the approach of generative adversarial networks (GANs). The discriminator network is responsible for distinguishing between the real input signal and the reconstructed signal, while the autoencoder strives to trick the discriminator network into making mistakes. The goal is to improve the realism of the output, even if it means further deviating from the input signal. At the beginning of training, adversarial loss is often temporarily disabled to avoid instability during training.
Below is a more detailed diagram showing the first phase of training and explicitly showing the other networks that typically play a role in this process.
Here is a more detailed version of the diagram for the first training phase, showing all participating networks.
It goes without saying that this general approach often has variations in applications such as audio and video, but I have tried to summarize the main elements that are common in most modern real-world applications.
How We Got Here
Today, the two main generative modeling paradigms, autoregressive and diffusion models, were originally applied to "raw" digital perceptual signals, i.e. pixels and waveforms. For example, PixelRNN and PixelCNN generate images pixel by pixel, while WaveNet and SampleRNN generate audio waveforms sample by sample. In the case of diffusion models, the original works that introduced and established this modeling paradigm generated images from pixels, while early works such as WaveGrad and DiffWave generated sound by generating waveforms.
However, it was quickly realized that this strategy was challenging to scale. The main reason for this can be summarized as follows: perceptual signals are mostly composed of imperceptible noise. In other words, out of the total amount of information in a given signal, only a small fraction actually affects our perception. Therefore, it is very important to ensure that our generative models can efficiently utilize their capacity and focus on modeling this small fraction of information. This way, we can use smaller, faster, and cheaper generative models without sacrificing perceptual quality.
Latent Autoregressive Model
Image autoregressive models took a giant leap forward with the publication of the landmark VQ-VAE paper, which proposed a practical strategy for learning discrete representations with neural networks by inserting a vector quantization bottleneck layer into an autoencoder. To learn a discrete latent representation of an image, a convolutional encoder with multiple downsampling stages generates a spatial grid of vectors at 4x lower resolution than the input image (1/4th the height and width, so 16x fewer spatial locations), which are then quantized through a bottleneck layer.
Now, we can use models like PixelCNN to generate latent vectors one at a time, rather than generating images pixel by pixel. This significantly reduces the number of autoregressive sampling steps required, but more importantly, measuring the likelihood loss in latent space rather than pixel space helps avoid wasting model capacity on imperceptible noise. This is effectively a different loss function that focuses more on perceptually relevant signal content, since much perceptually irrelevant signal content is not present in the latent vector (see my blog post on typicality for more on this). The paper showed 128×128 images generated from a model trained on ImageNet, a resolution that was only achievable with GANs at the time.
Discretization was crucial to its success, as autoregressive models at the time performed better with discrete inputs. But perhaps more importantly, the spatial structure of the latent representation made it very easy for existing pixel-based models to adapt. Prior to this, variational autoencoders (VAEs) typically compressed the entire image into a single latent vector, resulting in a representation without any topological structure. The grid structure of modern latent representations mirrors the grid structure of the “raw” input representations, and network architectures for generative models exploit this structure for efficiency (e.g., via convolutions, recurrent, or attention layers).
VQ-VAE 2 further increased the resolution to 256×256 and significantly improved the image quality by scaling up and using multi-level latent grids (organized in a hierarchical structure). Subsequently, VQGAN combined the adversarial learning mechanism of GANs with the VQ-VAE architecture. This increased the resolution reduction factor from 4x to 16x (256x fewer spatial locations compared to the pixel input) while still being able to generate sharp and realistic reconstructed images. The adversarial loss plays an important role in this, encouraging the generation of realistic decoder outputs even if they cannot closely follow the original input signal.
VQGAN has been at the heart of our rapid progress in generative modeling of perceptual signals over the past five years. Its impact cannot be overstated — I would even go so far as to say that it may be the main reason why GANs won the “Test of Time Award” at the 2024 NeurIPS conference. The “assist” provided by the VQGAN paper has kept GANs relevant even after they were almost completely replaced by diffusion models for the basic task of media generation.
It’s worth noting that many of the methods mentioned in the previous section were conceived in this paper. Today, iterative generators are generally not autoregressive (Parti, xAI’s recent Aurora model, and OpenAI’s GPT-4o are notable exceptions), and quantization bottlenecks have been replaced, but everything else is still there. In particular, the combination of simple regression loss, perceptual loss, and adversarial loss has stubbornly persisted despite its seeming complexity. This persistence is extremely rare in the rapidly evolving field of machine learning — perhaps only rivaled by the largely unchanged Transformer architecture and the Adam optimizer!
(While discrete representations are crucial in making latent autoregressive models useful in large-scale applications, I would like to point out that autoregressive models in continuous space have also recently achieved good results.)
Potential spread
With latent autoregressive models coming to the fore in the late 2010s and diffusion models making their mark in the early 2020s, combining the strengths of these two approaches became a natural next step. As with many ideas that emerge from a need for change, we saw a flurry of papers published on arXiv in the second half of 2021 exploring this topic. The most notable of these is High-Resolution Image Synthesis with Latent Diffusion Models by Rombach et al., who built on their previous VQGAN work and swapped out the autoregressive Transformer for a UNet-based diffusion model, which formed the basis for a stable diffusion model. Other related work, albeit smaller in scale or targeting non-image data, has explored similar issues.
It took some time for this approach to become mainstream. Early commercial image processing models used so-called resolution cascades, where a base diffusion model directly generated a low-resolution image in pixel space, and one or more upsampled diffusion models generated high-resolution outputs based on the low-resolution input. Typical examples include DALL-E 2 and Imagen 2. After the advent of stable diffusion models, most of them switched to latent space-based methods (including DALL-E 3 and Imagen 3).
A key difference between autoregressive and diffusion models is the loss function used for training. Autoregressive models are relatively simple to train, maximizing the likelihood (although other approaches have been tried). Diffusion models are more complex, with the loss function being the expectation over all noise levels, and the relative weights of these noise levels significantly influence what the model learns. This provides a basis for interpreting the typical diffusion loss as a perceptual loss function that places greater emphasis on signal content that is perceptually more salient.
At first glance, this makes the two-stage approach seem redundant, since it works in a similar way to the diffusion loss function, filtering out perceptually irrelevant signal content and avoiding wasting model capacity. However, in practice, the two mechanisms are quite complementary for the following reasons:
There appear to be fundamental differences in how perception works at small and large scales, especially in the field of vision. For example, modeling texture and fine-grained details requires separate treatments, and adversarial methods may be more suitable. I will discuss this in more detail below.
Training large and powerful diffusion models is computationally intensive, and using a more compact latent space avoids processing cumbersome input representations, helping to reduce memory requirements and speed up training and sampling.
There was indeed some early work that attempted an end-to-end approach, jointly learning a latent representation and a diffusion prior, but it did not catch on. Although it is desirable from a practical point of view to avoid sequence dependencies in multi-stage training, the perceptual and computational advantages make the trouble worthwhile.
Why are two stages needed?
As mentioned before, it is crucial to ensure that generative models of perceptual signals can efficiently utilize their capacity, as this makes them more cost-effective. This is essentially what the two-stage approach achieves: by extracting a more compact representation that focuses on the perceptually relevant parts of the signal content and modeling this representation instead of the original representation, we are able to make relatively small generative models perform well beyond their size.
The fact that the information in most perceptual signals is actually perceptually unimportant is not new: this is the key idea behind lossy compression, which allows us to store and transmit these signals more cheaply. Compression algorithms like JPEG and MP3 exploit redundancy in the signal and the fact that we are more sensitive to low frequencies than high frequencies, allowing us to represent the perceptual signal with fewer bits. (There are other perceptual effects, such as auditory masking, but non-uniform frequency sensitivity is the most important.)
So why don’t we build generative models on top of these lossy compression techniques? This isn’t a bad idea, and some research does use these algorithms or parts of them for this purpose. But we naturally tend to attack the problem with more machine learning to see if we can outperform these “hand-crafted” algorithms.
This is not just the arrogance of machine learning researchers: there is actually a very good reason to use learned latent representations instead of pre-existing compressed representations. Unlike the compression setting, where smaller is better and size is the only factor that matters, the goal of generative modeling imposes additional constraints: some representations are easier to model than others. Crucially, some structure is preserved in the representation, which we can exploit by giving the generative model an appropriate inductive bias. This requirement creates a trade-off between the quality of the reconstruction and the modelability of the latent representation, which we will explore in the next section.
Another important reason for the effectiveness of latent representations is how they exploit the fact that our perception works differently at different scales. In the audio domain, this is obvious: fast changes in amplitude give rise to the perception of pitch, while changes at coarser time scales (such as drum beats) can be discerned individually. Less well known is that this phenomenon also plays a role in visual perception: fast local fluctuations in color and intensity are perceived as texture. I tried to explain this on Twitter, and I’ll paraphrase that explanation here:
One way to think about it is texture versus structure, or what people sometimes call stuff versus object.
In an image of a dog in a field, the texture of grass (stuff) is high entropy, but we are not good at perceiving the differences between instances of this texture, we just perceive it as uncountable "grass". We don't need to look at each blade of grass one by one to be sure that we are looking at a field.
This slightly different implementation of texture is usually not noticeable unless you stack the images directly on top of each other. Experimenting with adversarial autoencoders is interesting: when you compare the original image and the reconstructed image side by side, they often look identical. But if you stack them on top of each other and switch back and forth, you can often see differences between the images, especially in areas with rich texture.
This is not the case for objects (tangible things), such as a dog's eyes, where differences in degree of similarity are immediately apparent. A good latent representation abstracts the texture but tries to preserve the structure. This way, the representation of a grass texture in a reconstruction can be different from the original without noticeably affecting the fidelity of the reconstruction. This allows the autoencoder to discard many patterns (i.e., other representations of the same texture) and more succinctly represent the presence of that texture in its latent space.
This in turn should also make generative modeling in the latent space easier, as it can now model the presence or absence of texture without having to capture all the complex variations associated with that texture.
A picture of a dog in a field. The top half of the image has low entropy: the pixels that make up the sky can be easily predicted from their neighbors. The bottom half has high entropy: the texture of the grass makes it hard to predict nearby pixels.
Because of the significant efficiency gains that the two-stage approach offers, it seems we are willing to tolerate the extra complexity it brings - at least for now. This efficiency gain not only makes training runs faster and cheaper, but more importantly, it also greatly speeds up sampling. For generative models that perform iterative refinement, this significant cost reduction is very welcome, as generating a single sample requires multiple forward passes through the model.
Tradeoff between reconstruction quality and modelability
It is worthwhile to explore the differences between lossy compression and latent representation learning in depth. While machine learning can be used for both, most lossy compression algorithms in widespread use today do not use machine learning. These algorithms are typically based on rate-distortion theory, which formalizes and quantifies the relationship between how much we can compress a signal (the rate) and how much we allow the decompressed signal to deviate from the original (the distortion).
For latent representation learning, we can extend this tradeoff by introducing the notion of modelability or learnability, which describes how hard it is for a generative model to capture this distribution of representations. This leads to a three-way rate-distortion modelability tradeoff, which is closely related to the rate-distortion usefulness tradeoff discussed by Tschannen et al. in the context of representation learning. (Another popular extension of this tradeoff in the context of machine learning is the rate-distortion perceptual tradeoff, which explicitly distinguishes between reconstruction fidelity and perceptual quality. To avoid overcomplication, I will not make this distinction here, and instead view distortion as a quantity measured in perceptual space, rather than input space.)
It’s not immediately obvious why this is even a tradeoff — why does modelability conflict with distortion? To understand this, consider the way lossy compression algorithms work: they exploit known signal structure to reduce redundancy. In the process, this structure is typically removed from the compressed representation, since the decompression algorithm is able to reconstruct it. But structure in the input signal is also widely exploited in modern generative models, for example in the form of architectural inductive biases that exploit signal properties like variability like translation or specific features of the frequency spectrum.
If we had a magical algorithm that could efficiently remove almost all redundancy from the input signal, we would make it very difficult for the generative model to capture the remaining unstructured variability in the compressed signal. This is perfectly fine if our goal is just compression, but not if we are doing generative modeling. Therefore, we have to find a balance: a good latent representation learning algorithm will detect and remove some redundancy, but also preserve some signal structure so that there is something left for the generative model to exploit.
A bad example in this context is entropy coding, which is actually a lossless compression method, but is also used as the final stage in many lossy schemes (e.g. Huffman coding in JPEG/PNG, or arithmetic coding in H.265). Entropy coding algorithms reduce redundancy by assigning shorter representations to frequently occurring patterns. This does not remove any information, but it destroys the structure. As a result, small changes in the input signal can lead to larger changes in the corresponding compressed signal, making entropy coded sequences much more difficult to model.
In contrast, latent representations tend to preserve a lot of signal structure. The figure below shows a visualization of the Stable Diffusion latent representations of some images (taken from the EQ-VAE paper). The animals can be easily identified just by visually inspecting the latent representations. They basically look like noisy low-resolution images with distorted colors. This is why I like to think of image latent representations as just "advanced pixels", capturing some extra information that normal pixels wouldn't capture, but mostly still behaving like pixels.
Visualization of Stable Diffusion latent representations extracted from several images, taken from the EQ-VAE paper. The first three principal components of the latent space correspond to the color channels. From visual inspection of the latent representations, the animals in the images are still mostly recognizable, indicating that the encoder retains a lot of the structure of the original signal.
Arguably, these latent representations are quite low-level. While traditional variational autoencoders (VAEs) compress the entire image into a feature vector, often resulting in a high-level representation that can be manipulated semantically, modern latent representations for generative image modeling are actually closer to the pixel level. They have higher capacity and inherit the grid structure of the input (albeit at a lower resolution). Each latent vector in the grid may abstract away some low-level image features, such as texture, but it does not capture the semantics of the image content. This is also why most autoencoders do not use any additional conditioning signals, such as text descriptions, as these signals mainly constrain the high-level structure (although there are exceptions).
Controllability
Two key design parameters control the capacity of a latent space with a grid structure: the downsampling factor and the number of channels in the representation. If the latent representation is discrete, the codebook size is also important because it imposes a hard limit on the number of bits of information that the latent representation can contain. (In addition to these, regularization strategies also play an important role, but we will discuss their impact in the next section.)
As an example, the encoder might take as input a 256×256 pixel image and produce a 32×32 continuous latent vector grid with 8 channels. This can be achieved by using a stack of strided convolutions or a visual transformer (ViT) with a patch size of 8. The downsampling factor reduces the dimensionality in both width and height, so there are 64 times fewer latent vectors than pixels — but each latent vector has 8 components, while each pixel has only 3 (RGB).
Overall, the latent representation has fewer tensor components (i.e., floating point numbers) than the tensor representing the original image. I like to call this number the tensor size reduction factor (TSR) to avoid confusion with the spatial or temporal downsampling factors.
Diagram showing the input and latent dimensions described in the text.
If we increase the encoder downsampling factor by a factor of 2, the size of the latent grid becomes 16×16, and we can then increase the number of channels by a factor of 4 to 32 channels to keep the same TSR (Total Spatial Redundancy). For a given TSR, there are often several different configurations that perform roughly equivalent in terms of reconstruction quality, especially in the case of video where we can control the temporal and spatial downsampling factors separately. However, if we change the TSR (either by changing the downsampling factor without changing the number of channels, or vice versa), this often has a profound impact on reconstruction quality and modelability.
From a purely mathematical point of view, this is surprising: if the latent variables are real-valued, the size of the grid and the number of channels should not matter, since the information capacity of a single number is already infinite (this is neatly demonstrated by Tupper's self-referential formula). But of course, there are practical constraints that limit the amount of information that a single component of the latent representation can carry:
We use floating point numbers to represent real numbers, and the precision of floating point numbers is limited;
In many formulas, the encoder adds a certain amount of noise, which further limits the effective accuracy;
Neural networks are not good at learning highly nonlinear functions of their input.
The first reason is obvious: if you use 32 bits (single precision) to represent a number, then it can only convey 32 bits of information at most. Adding noise will further reduce the number of usable bits, because some of the lower digits will be obscured by the noise.
The last restriction is more stringent, but not as well understood: aren’t neural networks meant to learn nonlinear functions? True, but neural networks naturally tend to learn relatively simple functions. This is usually a strength, not a weakness, because it increases the probability that the learned function will generalize to unseen data. But if we want to compress a lot of information into a few numbers, this will likely require a high degree of nonlinearity. While there are methods that can help neural networks learn more complex nonlinear functions (such as Fourier features), in our scenario, highly nonlinear mappings actually have a negative impact on modelability: they mask the signal structure, so this is not a good solution. Representations with more components offer a better trade-off.
The same is true for discrete latent representations: discretization sets a hard upper limit on the information content of the representation, but whether this capacity can be efficiently utilized depends mainly on the expressiveness of the encoder and the effectiveness of the quantization strategy in practice (i.e., whether high codebook utilization is achieved by using different codewords as evenly as possible). The most commonly used one is still the original VQ bottleneck in VQ-VAE, but a recent improvement that provides better gradient estimates through the "rotation trick" seems promising in terms of codebook utilization and end-to-end performance. Some alternatives that do not use explicitly learned codebooks are also gaining attention, such as finite scalar quantization (FSQ), lookup-free quantization (LFQ), and binary spherical quantization (BSQ).
In summary, choosing the right TSR (total spatial redundancy) is crucial: larger potential representations lead to better reconstruction quality (higher rate, lower distortion), but may have a negative impact on modelability. Larger representations mean more information bits need to be modeled, so the generative model needs to have a higher capacity. In practice, this trade-off is usually adjusted through experience. This can be a costly process, as there is currently no reliable and computationally inexpensive proxy for modelability. Therefore, it is necessary to repeatedly train a sufficiently large generative model to get meaningful results.
Hansen-Estruch et al. recently conducted an extensive exploration of latent space capacity and its various influencing factors (their key findings are clearly highlighted in the paper). There is a trend to increase the spatial downsampling factor and correspondingly increase the number of channels to maintain TSR for image and video generation at higher resolutions (e.g., 32× in LTX-Video, 44× in GAIA-2, and 64× in DCAE).
Sorting out and shaping potential space
So far, we have discussed the capacity of the latent representation, i.e. how many bits of information should be contained in it. It is also important to control exactly which bits of information from the original input signal should be retained in the latent representation, and how this information is presented. I will refer to the former as combing the latent space and the latter as shaping the latent space - this distinction is subtle but important. Many regularization strategies have been designed to shape, comb, and control the capacity of the latent representation. I will focus on the continuous case, but many of these considerations apply equally to discrete latent representations.
VQGAN and KL regularized latent variables
Rombach et al. proposed two regularization strategies for continuous latent spaces:
Following the original VQGAN design concept, we reinterpret the quantization step as part of the decoder (rather than the encoder) to obtain a continuous latent representation (i.e., VQ regularization, VQ-reg);
Completely remove the quantization operation in VQGAN and instead introduce a KL divergence penalty term (i.e. KL regularization, KL-reg) like the standard variational autoencoder (VAE).
The idea of making minimal changes to VQGAN to fit the Diffusion Model to generate continuous latent variables is ingenious: such structures perform well in autoregressive models, and the quantization step in the training process also acts as a kind of "safety valve" to prevent the latent variables from carrying too much information.
However, as we discussed before, this mechanism may not be truly necessary in most cases, as the expressiveness of the encoder is often the bottleneck of the generative model performance.
In contrast, KL regularization itself is a core component of the traditional VAE architecture: it is one of the two losses that make up the Evidence Lower Bound (ELBO). The ELBO is a lower bound on the data likelihood that is used to indirectly, but numerically, maximize the log-likelihood of the sample. This regularization encourages the latent variables to follow a pre-set prior distribution (usually a Gaussian distribution).
But the key point is that ELBO is only a true lower bound on likelihood when no scale parameter is introduced before the KL term. However, in practical applications, for the sake of training stability and reconstruction quality, the KL regularization term is almost always greatly scaled (usually reduced by several orders of magnitude), which almost cuts off its connection with the original context of variational inference.
The reason for this adjustment is also very direct: the unscaled KL term has too strong a restrictive effect, which will significantly compress the capacity of the latent space and seriously affect the quality of image reconstruction. For engineering feasibility considerations, the general practice in the industry is to significantly reduce its weight in the total loss function.
(By the way: adding KL weight is also an effective and common strategy in some tasks that focus more on semantic interpretability or latent variable disentanglement quality rather than reconstruction performance, such as β-VAE).
The following is obviously subjective, but I think there is still a lot of "mystification" in the current discussion about the effect of KL term. For example, KL term is widely believed to guide the latent variable to follow Gaussian distribution - however, under the scaling factors used in practical applications, this effect is so weak that it can be almost ignored. Even in "real" VAE, the aggregate posterior distribution rarely exhibits a standard Gaussian shape.
Therefore, in my opinion, the "V" in "VAE" (i.e. "Variational") has almost lost its real meaning now - its existence is more of a historical legacy. Instead, we might as well call this type of model "KL-regularised autoencoders", which is more conceptually appropriate for current mainstream practice.
In this setting, the main role of the KL term is to suppress outliers in the latent variable distribution and constrain its numerical scale to a certain extent. In other words: although the KL term is usually described as a mechanism to limit the capacity of the latent variable, its role in reality is more of a mild restriction on the shape of the latent variable - and this restriction is far less strong than imagined.
Adjusting the reconstruction loss
The "three-piece set" of reconstruction losses (regression loss, perceptual loss, and adversarial loss) undoubtedly plays a key role in maximizing the quality of the reconstructed signal.
However, it is worth further investigating how these loss terms affect the latents, especially in terms of "curation" (i.e., what information the latents learn to encode). As discussed in Section 3 (Why two stages?), in the visual domain, a good latent space should achieve some degree of abstraction of texture. How do these losses help achieve this?
An instructive thought experiment is to assume that we remove the perceptual loss and the adversarial loss and keep only the regression loss, as is done in traditional variational autoencoders (VAEs). This setting usually leads to blurry reconstructions. The regression loss is designed not to favor a particular type of signal content, so in image tasks it tends to focus more on low-frequency information simply because it accounts for a larger proportion of the image.
In natural images, the energy of different spatial frequencies is usually inversely proportional to the square of their frequency — the higher the frequency, the lower the energy (see my previous blog post for a graphical analysis of this phenomenon). Since high-frequency components account for a very small proportion of the total signal energy, when using regression loss, the model is more likely to accurately predict low-frequency components rather than high-frequency parts.
However, from the perspective of human perception, the subjective importance of high-frequency information is much higher than its proportion in the signal energy, which leads to the well-known "blurry" reconstruction result.
Image from the VQGAN paper. Comparison with DALL-E VAE trained with regression loss only shows the significant impact of perceptual and adversarial losses.
Since texture is mainly composed of these high-frequency components, and regression loss almost ignores these high-frequency information, the latent space we finally get not only fails to make texture abstraction, but directly erases the information related to texture. From the perspective of perceptual quality, this is a very poor latent space structure. This also directly illustrates the importance of perceptual loss and adversarial loss: they ensure that certain texture information can be encoded in the latent variable.
Since regression loss has these undesirable properties and often requires other loss terms to compensate for it, can we simply abandon it completely? It turns out that this approach is not feasible either. This is because the optimization process of perceptual loss and adversarial loss is more complicated and prone to pathological local optimal solutions (after all, these losses are usually built based on pre-trained neural networks). During the training process, regression loss plays the role of a "regularizer", continuously providing constraints and guidance for the optimization process to prevent the model from falling into the wrong parameter space.
There are many strategies that try to use different forms of reconstruction loss. The following are just some examples from the literature to show the diversity in this direction:
The DCAE46 model mentioned above has an overall approach that is similar to the original VQGAN recipe, except that the L2 regression loss (mean squared error, MSE) is replaced by the L1 loss (mean absolute error, MAE). It still retains the LPIPS perceptual loss (Learned Perceptual Image Patch Similarity) and the PatchGAN49 discriminator. The difference in this approach is that it uses multi-stage training, with adversarial loss enabled only in the final stage.
The ViT-VQGAN50 model combines two regression losses: L2 loss and logit-Laplace loss51, and uses the StyleGAN52 discriminator and LPIPS perceptual loss.
The LTX-Video44 model introduces a "video-aware loss" based on Discrete Wavelet Transform (DWT) and proposes its own unique adversarial loss strategy called reconstruction-GAN.
Just as classic dishes have different tastes for different people, every researcher has his or her own solution to this "recipe" problem!
Representation Learning vs Reconstruction
Many of the design choices we have discussed so far affect not only the quality of reconstruction, but also the properties of the learned latent space. Among them, the reconstruction loss actually undertakes a dual task: it not only ensures the high quality of the decoder output, but also plays a key role in the formation of the latent space. This can't help but raise a question: Is it really appropriate to "kill two birds with one stone" as we are doing now? I think the answer is no.
Modern autoencoders are often expected to accomplish both of these tasks simultaneously: learning a good and compact representation for generative modelling and decoding this representation back into the original input space are two distinct tasks.
Although this works quite well from a practical point of view and undoubtedly simplifies the process (after all, autoencoder training is already the first stage of training in the complete system, and we naturally want to avoid further complexity as much as possible, although it is not unheard of to train autoencoders in multiple stages). However, this approach actually confuses the two tasks, and some designs that are suitable for one task may not be ideal for the other task.
This problem of task merging is particularly acute when the decoder adopts an autoregressive architecture, so we propose to use an independent non-autoregressive auxiliary decoder to provide a learning signal for the encoder.
The main decoder does not affect the latent representation at all, as its gradients are not back-propagated to the encoder during training. This allows it to focus on optimizing the reconstruction quality, while the auxiliary decoder takes on the task of shaping the latent space. The entire autoencoder components can still be trained jointly, so the added training complexity is very limited. Although the auxiliary decoder adds training cost, it can be discarded after training is completed.
In this autoencoder structure with two decoders: the main decoder is only used for reconstruction and its gradients are not passed back to the encoder (usually we use dotted lines to indicate this), while the auxiliary decoder focuses on building the latent space. It can adopt different architectures, optimize different loss functions, or both.
Although the idea of using an autoregressive decoder to process the pixel space in that paper is no longer applicable (arguably anachronistic), I still believe that this strategy of separating representation learning from the reconstruction task is still highly relevant today.
An auxiliary decoder, if it optimizes a different loss or adopts a different architecture from the main decoder (or both), may provide a more effective training signal for representation learning, leading to better generative modeling results.
Zhu et al. recently came to the same conclusion (see Section 2.1 of their paper), using K-means to discretize the features extracted by DINOv2 and combine it with a separately trained decoder. The idea of reusing representations obtained by self-supervised learning in generative modeling has long been common in the field of audio modeling - probably because researchers in the audio field are accustomed to training vocoders to convert predefined intermediate representations (such as mel-spectrograms) back to waveform signals.
Improving model performance through regularization
Shaping, organizing, and limiting the capacity of latent variables all affect their modelability:
The capacity limit determines the amount of information in the latent variables. The higher the capacity, the more powerful the generative model must be to fully capture all the information it contains;
Shaping is critical to achieving efficient modeling. The same information can be represented in many different ways, some of which are easier to model than others. Scaling and normalization are critical to correct modeling (especially for diffusion models), but higher-order statistics and correlation structures are equally important;
Grooming affects modelability because some types of information are easier to model than others. If the latent variables encode unpredictable noise information in the input signal, then they will also be less predictable.
Here’s an interesting tweet showing how this affects the Stable Diffusion XL VAE:
Image source: https://x.com/rgilman33/status/1911712029443862938
Here, I want to connect this to the V-information proposed by Xu et al., which extends the concept of mutual information to take into account computational constraints. In other words, the availability of information depends on how computationally difficult it is for an observer to discern the information, and we can try to quantify this. If a piece of information requires a powerful neural network to extract, then the amount of V-information in the input will be lower than if a simple linear probe was used - even if the absolute amount of information in bits is the same.
Obviously, maximizing the amount of V-information in the latent representation is desirable in order to minimize the computational requirements required for the generative model to understand the latent representation. The rate-distortion-utility tradeoff described by Tschannen et al. that I mentioned earlier also supports the same conclusion.
As mentioned before, the KL penalty may not do as much to Gaussianize or smooth the latent space as many people think. So, what can we do to make the latent space easier to model?
Use generative priors: jointly train a (lightweight) latent generative model with the autoencoder, and make the latent model easy to model by backpropagating the generative loss into the encoder, just like in LARP or CRT. This requires careful tuning of the loss weights, since the generation loss and the reconstruction loss are at odds with each other: the latent models are easiest to model when they encode no information at all!
Use pre-trained representations for supervision: The latent model is encouraged to make predictions on existing high-quality representations (e.g., DINOv2 features), as in VA-VAE, MAETok, or GigaTok.
Encourage equivariance: Make certain transformations of the input (e.g., rescaling, rotation) produce corresponding latent representations that also transform similarly, as in AuraEquiVAE, EQ-VAE, and AF-VAE. The graph from the EQ-VAE paper that I used in Part 4 shows the profound effect this constraint has on the spatial smoothness of the latent space. Skorokhodov et al. came to the same conclusion based on a spectral analysis of the latent space: equivariance regularization makes the latent spectrum more similar to the spectrum of the pixel-space input, thus improving modelability.
This is just a small sampling of possible regularization strategies, all of which attempt to increase the V-information of the latent vector in some way.
Spread downward
One class of autoencoders for learning latent representations is worth further investigation: autoencoders with diffusion decoders. While the more typical decoder architecture employs a feed-forward network that directly outputs pixel values in a single forward pass and employs adversarial training, an increasingly popular alternative is to use diffusion for the latent decoding task and to model the distribution of the latent representation. This affects not only the quality of the reconstruction, but also the type of representation learned.
SWYCC, ϵ-VAE, and DiTo are some recent works exploring this approach from several different perspectives:
Latent features learned using diffusion decoders provide a more principled, theoretically grounded approach to hierarchical generative modeling;
They can be trained using only the MSE loss, which simplifies the process and improves robustness (after all, adversarial losses are quite tricky to tune);
Applying the principle of iterative improvement to decoding can improve the output quality.
I can’t argue with these points, but I do want to point out a significant weakness of diffusion decoders: their computational cost and its impact on decoder latency. I believe that a key reason why most commercially deployed diffusion models today are latent models is that the compact latent representation helps us avoid iterative refinement in the input space, which is slow and expensive. It is much faster to perform the iterative sampling process in the latent space and then do a single forward propagation back to the input space at the end. With this in mind, it seems to me that reintroducing iterative refinement of the input space in the decoding task largely defeats the purpose of the two-stage approach. If we are going to pay this price, we might as well choose some simple diffusion methods to extend the single-stage generative model.
But wait, you might say — can’t we just use one of the many diffusion distillation methods to reduce the number of steps required? In such settings, due to the very rich conditioning signal (i.e., latent representation), these methods have indeed been shown to be effective, even in a single-step sampling regime: the stronger the conditioning, the fewer steps are needed to obtain a high-quality distillation result.
The consistent decoder of DALL-E 3 is a good example of this: they reused the stable diffusion latent space and trained a new diffusion-based decoder, which was then reduced to only two sampling steps through consistent distillation. Although it is still more expensive than the original adversarial decoder in terms of latency, the visual fidelity of the output is significantly improved.
DALL-E 3’s consistent decoder based on the Stable Diffusion latent space significantly improves visual fidelity, but at the expense of higher latency.
Music2Latent is another example of this approach, operating on spectrogram representations of musical audio. Their autoencoder with a consistent decoder is trained end-to-end (unlike the autoencoder in DALL-E 3, which reuses a pre-trained encoder) and is able to generate high-fidelity output in a single step. This means that the decoding process again requires only a single forward pass, just like the adversarial decoder.
FlowMo is an autoencoder with a diffusion decoder that uses a post-training stage to encourage mode-searching behavior. As mentioned before, for the task of decoding latent representations, losing modality and focusing on realism rather than diversity is actually desirable because it requires less model capacity and does not negatively impact perceptual quality. Adversarial losses tend to cause modality loss, but diffusion-based losses do not. This two-stage training strategy enables the diffusion decoder to mimic this behavior — although it still requires a large number of sampling steps and is therefore much more computationally expensive than a typical adversarial decoder.
Some early studies on diffusion autoencoders, such as Diff-AE and DiffuseVAE, focus more on learning high-level semantic representations similar to old-style VAEs, without topological structures, and focusing on controllability and decoupling. DisCo-Diff is somewhere in between, which enhances the diffusion model with a series of discrete latent representations that can be modeled by autoregressive priors.
Removing the need for adversarial training would certainly simplify things, so diffusing autoencoders are an interesting (and recently quite popular) area of research in this regard. However, it seems challenging to be competitive with adversarial decoders in terms of latency, so I don't think we're ready to give up on them just yet. I'm very much looking forward to a newer scheme that doesn't require adversarial training but is comparable to current adversarial decoders in terms of visual quality and latency!
The grid rules them all
Digital representations of perceptual modalities often have a grid structure because they are uniformly sampled (and quantized) versions of the underlying physical signal. Images result in a 2D grid of pixels, videos result in a 3D grid, and audio signals result in a 1D grid (i.e., sequence). Uniform sampling means that there is a fixed quantum (i.e., distance or amount of time) between adjacent grid positions.
Perceptual signals also tend to be approximately stationary in time and space, statistically speaking. Combined with uniform sampling, this yields rich topological structure, which we exploit when designing neural network architectures to process them: using extensive weight sharing to exploit properties such as invariance and equivariance, which are achieved through convolutions, recurrences, and attention mechanisms.
It’s no surprise that exploiting the grid structure is one of the key reasons why we’re able to build such powerful machine learning models. As a corollary, it’s a very good idea to preserve this structure when designing your latent space. Our most powerful neural network designs rely on it architecturally because they were originally built to process these digital signals directly. They’ll be much better at processing latent representations if they have the same structure.
The grid structure also brings significant advantages to autoencoders that learn to generate latent spaces: due to stationarity, and because they only need to learn local signal structure, they can be trained on smaller crops or fragments of the input signal. If we impose the right architectural constraints (limiting the receptive fields at each position in the encoder and decoder), they will be able to generalize out of the box to larger grids than they were trained on. This has the potential to significantly reduce the cost of first-stage training.
However, things are not always rosy: we have already discussed how perceptual signals are highly redundant, and unfortunately, this redundancy is not evenly distributed. Some parts of the signal may contain a lot of perceptually salient detail, while other parts contain little information. In the image of a dog in a field that we used earlier, consider a 100×100 pixel patch centered on the dog’s head and compare it to a 100×100 pixel patch in the upper right corner of the image that contains only the blue sky.
Image of a dog in a field, with two 100×100 pixel patches with different redundancies highlighted.
If we construct a latent representation that inherits the 2D grid structure of the input and use it to encode this image, we will inevitably use exactly the same capacity to encode both patches. If we make the representation rich enough to capture all the relevant perceptual details of the dog's head, a lot of capacity will be wasted encoding similar-sized patches of the sky. In other words, preserving the grid structure will significantly reduce the efficiency of the latent representation.
This is what I mean by "grids rule them all": our ability to process grid-structured data with neural networks is so well established that deviating from this structure increases complexity, makes the modeling task more difficult, and is less compatible with hardware, so it is usually not done. But in terms of coding efficiency, it is actually quite wasteful because perceptually salient information in audiovisual signals is not evenly distributed.
The Transformer architecture is actually relatively well suited to combat this domination: while we often think of it as a sequence model, it is actually designed to process set-valued data, and any additional topological structure relating the elements of the set to each other is expressed via positional encodings. This makes deviations from the regular grid structure more practical than convolutional or recurrent architectures. A few years ago, my colleagues and I explored this idea of using variable-rate discrete representations for speech generation. Relaxing the topology of the latent space seems to be gaining more and more attention recently in the context of two-stage generative models, including the following:
TiTok and FlowMo learn sequence-structured latent representations from images, reducing the grid dimension from 2D to 1D. The development of large language models has given us extremely powerful sequence models, so this is a reasonable target structure;
One-D-Piece and FlexTok take a similar approach, but use a nested dropout mechanism to introduce a coarse-to-fine structure in the latent sequence. This allows the sequence length to be adjusted based on the complexity of each input image and the level of detail required for reconstruction. CAT also explores this adaptability, but still retains the 2D grid structure and only adjusts its resolution;
TokenSet goes a step further and uses an autoencoder that generates a "bag of tokens", abandoning the grid entirely.
What all of these methods have in common, with the exception of CAT, is that the latent spaces they learn are much more semantically advanced than the ones we have primarily discussed so far. In terms of level of abstraction, they are probably somewhere between “high-level pixels” and the vector-valued latent spaces of old-school VAEs. FlexTok’s 1D sequence encoder takes the low-level latent space of an existing 2D grid-structured encoder as input, effectively building an extra layer of abstraction on top of the existing low-level latent space. TiTok and One-D-Piece also leverage existing 2D grid-structured latent spaces as part of their multi-stage training methods. A related idea is to reuse the language domain as a high-level latent representation of images.
In the discrete setting, some work has explored whether common token patterns in a grid can be combined into larger subunits, leveraging ideas from language tokenisation: DiscreTalk is an early example in speech, which uses SentencePiece on top of VQ tokens. Zhang et al’s BPE Image Tokenizer is a more recent incarnation of this idea, which uses an enhanced byte pair encoding algorithm on top of VQGAN tokens.
Latent variables of other modalities
So far we have focused primarily on the vision domain, with only brief mentions of audio in a few places. This is because learning latent features for images is something we are already very good at, and image generation using two-stage approaches has been extensively studied and put into production in recent years! We have a mature body of research in perceptual losses, and a large number of discriminator architectures that enable adversarial training to focus on perceptually relevant image content.
For video, we still stay in the vision domain, but introduce the temporal dimension, which brings some challenges. One can simply reuse the latent features of the image and extract them frame by frame to obtain a latent video representation, but this can lead to temporal artifacts (such as flickering). More importantly, it cannot exploit temporal redundancy. I think our tools for spatiotemporal latent representation learning are far from perfect, and people's understanding of how to exploit human perception of motion to improve efficiency is not deep enough at present. This is still the case despite the fact that video compression algorithms all use motion estimation to improve efficiency.
The same is true for audio: while the two-stage approach has been widely adopted, there does not seem to be a broad consensus on the modifications required to make it applicable to this modality. As mentioned earlier, for audio, it is more common to reuse representations learned through self-supervised learning.
What about language? Language is not a perceptual modality, but could a two-stage approach perhaps also improve the efficiency of large language models? This turns out to be difficult. Language is inherently harder to compress than perceptual signals: it evolved as an efficient way to communicate, so redundancy is much lower. This doesn’t mean that language doesn’t exist: Shannon famously estimated that English has 50% redundancy. But remember that images, audio, and video can be compressed by orders of magnitude with relatively little perceptual distortion, whereas it is impossible to do the same with language without losing nuance or important semantic information.
Tokenisers used for language models tend to be lossless (e.g. BPE, SentencePiece), so the generated tokens are not usually considered "latent tokens" (however, the Byte Latent Transformer does use this framework in its dynamic tokenisation strategy). However, the relative lack of redundancy in language has not stopped people from trying to learn lossy high-level representations! Techniques used for perceptual signals may not be applicable, but several other approaches for learning sentence or paragraph level representations have been explored.
Will end-to-end be the ultimate winner?
When deep learning took off, the dominant view was that we would replace hand-crafted features with end-to-end learning whenever possible. Jointly learning all processing stages would allow them to adapt and collaborate with each other, maximizing performance while simplifying the process from an engineering perspective. This is more or less what ended up happening in computer vision and speech processing. From this perspective, i