Thanks to @Julian and @denisa for the corrections, suggestions and discussions!
Multiple Concurrent Proposers (MCP) has recently become a significant topic of discussion within the community, particularly following the introduction of the BRAID protocol and the rise of DAG consensus. Max’s argument in favor of MCP for Ethereum centers on the monopoly created by leader-based consensus mechanisms, where the leader for a given slot is granted substantial monopolistic power. This concentration of power leads to issues such as short censorship for some transactions.
In leader-based consensus, the designated leader for each slot has the exclusive authority to propose blocks, which allows them to exploit their position for profit maximization, such as through transaction reordering or frontrunning. MCP aims to mitigate these issues by decentralizing the block proposal process, reducing the influence any single proposer can exert over the network during a given slot.
Multiple Concurrent Proposers Economic Order
Let nn represent the number of validators in the network. A subset of validators maintains a local chain, denoted by k < nk<n. The protocol at some step will need to pick the union of all local blockchains at slot ii and an ordering rule must be applied between transactions of each local chain.
Deterministic Block Ordering: A deterministic rule is applied to order the blocks and its transactions. In the context of MEV-SBC ‘24 event, Max proposes two approaches:
- Sorting by Priority Fee: Blocks are sorted based on the priority fee of transactions. MEV (Maximal Extractable Value) taxes can be applied, where a percentage of the priority fee is extracted and redistributed by the application. This approach is detailed in the proposal “Priority is All You Need”.
- Execution Flags: Transactions can set an “execution flag” that indicates specific actions, such as interacting with a particular liquidity pool (e.g., trading ETH/USDC in the UNIv5 pool). When the block ordering rule encounters a transaction with such a flag, it pulls all flagged transactions attempting to interact with that pool and executes them as a batch.
Timing Games with Frontrunning Incentive
Let pp be a proposer participating in the MCP protocol, who is responsible for proposing a block in their local chain during slot ii. We acknowledge that there exists an inherent delay and processing time required to propose this block. Specifically, the protocol permits a maximum allowable delay of \DeltaΔ time units before pp incurs penalties.
pp may strategically opt to delay their block proposal until \Delta - \epsilonΔ−ϵ (where \epsilon > 0 ϵ>0) time units. This delay enables pp to potentially exploit a frontrunning opportunity by observing and computing a partial order of transactions submitted by other proposers. By strategically placing their block proposal just before the misslot penalty (no block has been proposed and it’s no going to be accepted for slot ii), pp could include transactions with higher gas fees, a situation that provides a clear incentive for engaging in frontrunning behavior and the main incentive for playing timing games in this post.
Under the current deterministic protocol rules, such a timing strategy is incentivized as it allows proposers to maximize their rewards through manipulation of transaction order. This situation underscores the need for an effective mechanism. However, a more robust solution may involve revisiting the transaction ordering rules to eliminate this concrete incentive for timing games that lead to such exploitative behaviors, thereby ensuring a fairer and more secure protocol.
Partially Ordered Dataset (POD)
One of the main concerns regarding MCP is the absence of a clearly defined method for determining the order of transactions. It remains uncertain how the sequence and the underlying criteria for ordering will be established, as well as how the influence of clients will be exercised—whether through mechanisms such as auctions, latency considerations, or the risk of spam attacks, as highlighted by Phil at SBC '24.
The team of Common Prefix has conducted a thorough analysis of various consensus protocols, including leader-based, inclusion list, and leaderless consensus models, with a focus on their resistance to censorship. As a result of their research, they developed the concept of a Partially Ordered Dataset. In this model, the order of transactions is determined by the timestamps recorded by the clients, which may lead to a lack of strict ordering when two transactions are recorded simultaneously. The implications of relinquishing strict ordering in transaction processing have not been extensively explored in the existing literature, or at least, I am not aware of any comprehensive studies on the matter.
A POD is a finite sequence of pair \{(r, T), …, (r’, T’)\}{(r,T),…,(r′,T′)} s.t. rr is round (slot) and TT a set of transactions.
A round is perfect r_{perf}rperf if no new transactions can appear with recorded round r_{rec} \leq r_{perf}rrec≤rperf, which means there is no conflict in the ordering before r_{perf}rperf.
A POD protocol exposes the following methods.
- input event
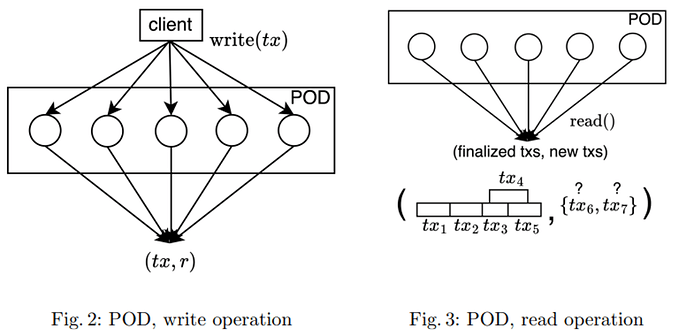
write(tx): Clients callwrite(tx)to write a transactiontx. - output event
write_return(tx, π): afterwrite(tx)the protocol outputswrite_return(tx, π), whereπis a record certificate. - input event
read_perfect(): Clients callread_perfect()to read the transactions in the bulletin. - output event
read_perfect_return(r, D, Π): afterread_perfect()protocol outputsread_perfect_return(r, D, Π), whereris a round, called the past perfect round,Lis a set of transactions,Dis a POD, andΠis a past-perfect certificate. For each entry(r', T)inD, we say that transactions inTbecame finalized at roundr'. - input event
read_all(): returns all transactions up to the current round without past-perfection guarantees, hence it can return faster thanread_perfect(). - output event
read_all_return(D, Π) identify(π, Π) → P' ⊆ P: Clients callidentify(π, Π) → P' ⊆ Pto identify the setP'of parties who vouched for the finalization of a transaction, whereΠis a POD andπis the certificate returned bywrite_return(tx, π).
The properties of Liveness and Security are detailed in the original work, and the following will be utilized in subsequent arguments:
Fair punishment: No honest replica gets punished as a result of malicious operation. If identify(π, Π) → P', where π is a record certificate for transaction tx and Π is a past-perfect certificate for a POD D, can only be created if all parties in P' sign tx and D.
The construction of the POD is as follows: The client will send a transaction to all the validators in the network and will have to wait for n - fn−f signatures to confirm his transaction has been received by the network, where ff is the amount of allowed byzantine validators. Once the client received the signature he will record the median of all the signatures he has received, as there is going to be some latency and difference between the validators when they received the transaction.
For the reading set of transactions for some round the client will have two options:
- Believe in synchrony on the txs received: Request all the recorded transactions from the validators for some specific round rr. Once obtains the n- fn−f signatures of all the transactions computes the median of the set of transactions based on their timestamps.
- Past-perfect guarantees, no-synchrony believer: Assume r_{perf}rperf to be the minimum of the received rr values, then we will not have any transaction with lower timestamp. Now takes the union of all the upcoming transactions. Now the client will have to wait some \deltaδ time to ensure through the gossip mechanism there is no lower r_{perf}rperf and no more transaction for the upcoming round.
PODs mitigating MEV in MCP
Adopting Partially Ordered Datasets (PODs) as the primary data structure for MCP introduces a novel approach that hasn’t been extensively studied, particularly regarding its potential to mitigate the types of MEV games previously described.
In PODs, transactions are ordered deterministically based on their timestamps. While this approach necessitates handling cases where multiple transactions share the same timestamp—or evaluating the likelihood of such occurrences—it fundamentally alters the dynamics of the fronturunning incentive of timing games previously described against other proposers block transactions.
Consider a scenario in slot mm where a malicious proposer attempts to front-run or sandwich another transaction. Under the previous deterministic ordering, which was based on auctions and priority fees, such attacks were feasible because proposers could manipulate their position in the ordering by outbidding others or exploiting latency. However, with timestamp-based ordering as implemented in PODs, this strategy changes significantly. An open question is still to know which strategies can be applied with PODs or timestamp ordering to extract MEV and if they are worse in wellfare of the network compared with the described game.
In this new setup, being the last proposer in a slot would actually place that proposer in the final position within the transaction order, limiting their ability to engage in front-running or sandwiching assuming honesty in all nodes. Instead, they would only be able to perform back-running, which is generally considered less harmful than front-running or sandwiching. This shift in ordering strategy could effectively reduce the risk of these more dangerous forms of MEV exploitation.
If a malicious validator attempts to manipulate the order of transactions by bribing proposers, slashing should be applied to the validator. By imposing such penalties, the protocol discourages malicious behavior and ensures that the integrity of the transaction ordering process is maintained. One of the future next questions it’s how can we detect a bad behaviour in the transaction record, maybe applying Turkey’s Method it’s a posible option and assume that outliers are malicious records.
However, the situation is more complex than it appears. The shift to a new game for validators, where transaction ordering is influenced by latency, introduces additional challenges. Validators may now engage in latency games, where geographical proximity to other validators or network nodes becomes a crucial factor in gaining an advantage. To mitigate this, it is essential to ensure that validators are well decentralized across different regions.
Decentralizing validators geographically helps reduce the impact of latency-based advantages. Validators clustered in the same location could lead to centralization risks, where a few validators might dominate the network due to their low-latency connections. This centralization could undermine the fairness of transaction ordering and potentially reintroduce the risk of censorship.
Moreover, validators are incentivized to avoid sharing the same location because doing so decreases the uniqueness of the transactions they can access for a possible backrunning and taking such opportunities. The more validators operate from the same region, the fewer unique transactions each can capture, leading to lower profits from transaction fees, as these would have to be split among more validators. This dynamic encourages validators to spread out, fostering a more decentralized and resilient network that is better protected against latency-based games and the centralization of power. However, the current incentive is still weak and future work will reside in how to provide better incentives for non-centralization.