Author: The Spartan Group
Translation: vernacular blockchain

The Bitcoin ecosystem in 2023 is full of excitement, reminiscent of the Ethereum community in 2017. Enthusiastic builders, investors, and community members are exploring the possibilities within the Bitcoin hierarchy. Given Ethereum’s impressive trajectory, Bitcoin is on the verge of exceeding or even surpassing these heights, thanks to its industry-leading market cap and Bitcoin dominance. Just as Bitcoin revolutionized trust when it debuted in 2009, the Bitcoin ecosystem is now at another critical moment as it moves closer to delivering on its original promise, paving the way for a truly trustless financial system rooted in its core L1 technology. the way.
The Bitcoin L2 market opportunity far exceeds other markets in the Bitcoin economy. To build any case about the total Bitcoin L2 market opportunity, the focus will be on the existing market for Ethereum L2. In the following estimate of Bitcoin’s L2 market cap, a guidance ratio between the total value locked (TVL) of all Ethereum L2s and Ethereum’s overall market cap is used, which is approximately 5.62% at the time of writing.
The pessimistic scenario suggests that the Bitcoin L2 market cap could reach $4.8 billion, accounting for only about 10% (0.56%) of the total Ethereum L2 market at the time of writing.
The basic situation shows that the Bitcoin L2 market capitalization can reach $24 billion, accounting for only about 50% (2.81%) of the total Ethereum L2 market at the time of writing.
Optimistic scenarios suggest that Bitcoin L2 market cap could reach $48 billion, matching 100% (5.62%) of the total Ethereum L2 market at the time of writing.
Given the current market sentiment regarding building on Bitcoin, the forecast is based on a two-year time horizon, does not account for additional annual growth, and assumes Bitcoin L2 continues to expand. The accelerated development and protocol standards of Bitcoin L2, as well as its connection to existing infrastructure, provide key factors for Bitcoin L2 to reach an estimated $24 billion market capitalization in 2025. The next section describes potential roadmap and industry events that could impact our bearish, base case, and bullish scenarios.
1. Immediate Outlook: The Continued Cultural Impact of Ordinal Numbers
In the short term, the cultural impact of ordinal numbers within the Bitcoin ecosystem remains an important driver. Ordinal’s unique appeal lies in its ability to integrate art and collectibles into the Bitcoin blockchain, deeply resonating with communities that value authenticity, creativity, and timelessness. This cultural resonance has solidified Ordinal’s place in the Bitcoin landscape and continues to attract and retain a diverse audience. By capturing the spirit of the digital age, they have expanded Bitcoin’s influence far beyond its original scope.
By the end of 2023, the rapid adoption of ordinal numbers has made Bitcoin one of the largest NFT platforms, even surpassing Solana without smart contract functionality. In November, Bitcoin NFT (ordinal) sales increased by a staggering 500%, surpassing Ethereum and Solana sales during the same period. While ordinal has only been around for about a year, data shows that assets deployed on Bitcoin are also able to command higher values due to their immutability and permanence on the Bitcoin network.
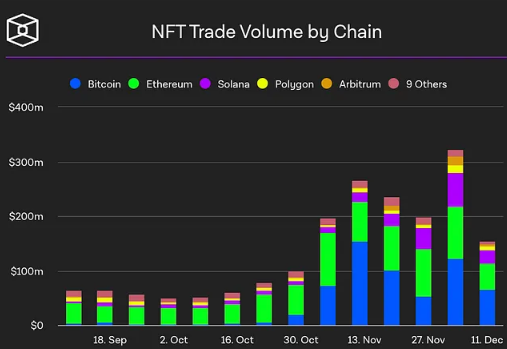
NFT transaction volume is broken down by chain. Source: The Block, CryptoSlam

On-chain Monkey NFTs double in price after creators staked them on Bitcoin. Source: Metagood
The growing popularity of Bitcoin NFTs, such as the OnChain Monkey NFT doubling in price after integrating with Bitcoin, shows that curiosity among users is growing. This will naturally lead users to explore further within the Bitcoin ecosystem, eager to learn more about other use cases such as DeFi and gaming. While this curiosity paves the way for significant change, much innovation still occurs at the protocol level because of inherent limitations such as transaction speed, smart contract compatibility , and scalability.
For example, many early projects in the ecosystem were unable to issue tokens with the same utility and governance capabilities as on Ethereum (such as BRC-20 vs. ERC-20). These projects must then rely on equity financing and cannot launch a community by leveraging their own tokens. Solutions include issuing fungible tokens on Stacks, providing smart contract functionality for the SIP-10 fungible token standard, or other emerging token standards. Two-way bridges, such as MultiBit for cross-network transfers between BRC-20 and ERC-20 Tokens, are emerging to address these gaps. However, these solutions are not the final solution. Continuous innovation is critical to overcoming these challenges. As L2 continues to make progress to lower transaction costs while inheriting 100% Bitcoin finality. At the same time, innovation is gradually emerging through Bitcoin L1. Despite these challenges, developers and enthusiasts have begun experimenting with various use cases.
Most of the innovation we see today still permeates through Bitcoin L1. Source: ALEX
2. Mid-term outlook: Bitcoin L2 breakthroughs and emerging use cases
In the medium term, the Bitcoin ecosystem is poised for major breakthroughs, driven primarily by advances in L2 technology, such as the Nakamoto version of Stacks and the introduction of sBTC. These developments are not just incremental, but transformative, especially in Bitcoin DeFi and other application areas.

A growing map of Bitcoin smart contracts and the Stacks ecosystem. Source: Stacks
The significant reduction in block times from over 10 minutes to 5 seconds enhances security, which is critical to creating a smooth, "Ethereum-like" user experience that will attract new developers, drive adoption and innovation cycle played a driving role.
The implementation of Fast Blocks and sBTC will enable Stacks to deliver high-performance, BTC-denominated applications such as NFT marketplaces, facilitating more efficient trading of Ordinals and unique L2 NFT collections.
The DeFi landscape on Bitcoin is expected to see considerable expansion, such as lending, which is enabled through sBTC. The Zest Protocol team has already built this functionality on Stacks ahead of time.
ALEX is preparing all DeFi features, has recently surpassed $500 million in trading volume, and has established the foundation for a swap market in sBTC for other sub-tokens. Each different application can be explored while generating automated Stacks-based earnings.
Unlock Bitcoin’s market capitalization and create a user adoption flywheel like Ethereum’s. As the infrastructure continues to mature, a series of new application use cases will emerge at various Bitcoin levels and gain recognition from end users. Not only does the Bitcoin ecosystem have the largest potential total value locked in the industry, it is also targeted at a much wider audience – built for mainstream users. Some of the key developments that make the ecosystem successful include:
Trust Machines is building Bitcoin applications that aim to grow the Bitcoin economy by proposing new Bitcoin use cases to maximize the value of the network.
In response to the expected influx of developers, Hiro is enhancing development tools for all layers of Bitcoin.
Wallets like Xverse, Leather, and Ryder focus on providing a seamless user experience for mass adoption, compatible with a variety of assets across all layers of Bitcoin.
With the rapid popularity of the Ordinal market, larger-scale centralized trading platforms have also been launched, such as Binance, Magic Eden and OKX. Other markets also emerged quickly, including Ordzaar, Gamma, etc. On-chain Monkey also recently launched its own marketplace, Osura.
Other notable developments include the first Bitcoin-based game from Ordz Games, which launched its BRC-20 Token $OG.
New Bitcoin City, a friendly technology equivalent project, was built on Bitcoin L2 NOS by Trustless Computer in October 2023, and its total locked value has exceeded US$1 million.
StackingDAO introduced the liquid stacking function in December 2023, realizing the liquidity stacking of Stacks by introducing liquid STX (stSTX).
Additionally, Darewise, part of Animoca Brands, is pioneering an Ordinal-based metaverse, showcasing the ever-expanding realm of possibilities within the Bitcoin ecosystem.
Bitcoin Application Snapshot March 2024
Ultimately, this L2-driven expansion of the Bitcoin ecosystem is not just about adding new features and attracting new users, but also more closely weaving Bitcoin into the global blockchain economy. Projects like ALEX are at the forefront of this movement, designing permissionless yield stablecoins native to BTC and BTC cross-chain bridges such as XLink to connect Bitcoin to Ethereum and other ecosystems . These initiatives are critical in fostering a Bitcoin ecosystem that is not only more connected, but also more efficient, laying the foundation for the emergence of various financial innovations and services within the industry over the long term.
In addition, the development of further scaling solutions on Stacks will greatly enhance the interoperability of the Bitcoin ecosystem with other blockchain networks at the L2 level. With the upcoming Nakamoto upgrade, Stacks will introduce new subnets supporting various programming languages and execution environments, including EVM subnets and Rust VM. Additionally, work is underway to integrate WASM support directly into Stacks L2, which will be activated in conjunction with the Nakamoto upgrade. In December 2023, a working group within the Stacks ecosystem released details about integrating the new ClarityWASM virtual machine . This integration will open the door to Rust, Solidity, and a wider range of languages directly within the Stacks L2 environment.
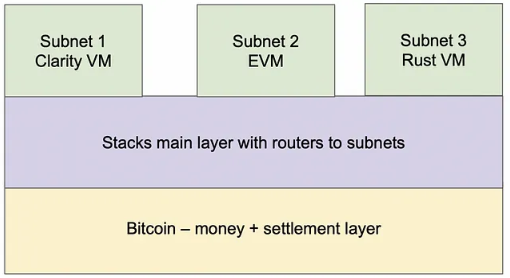
Stacks’ scalability is achieved through subnets and different virtual machines. Source: Stacks white paper
3. Long-term vision: Paving the way for institutional adoption
The long-term outlook for Bitcoin is its confirmation as a leader in institutional digital assets and DeFi adoption. The approval of a Bitcoin spot ETF is a key milestone that has the potential to revolutionize the way institutions engage with Bitcoin. This approval is expected to catalyze a major paradigm shift, with institutions increasingly focusing on Bitcoin-centric financial products and services. As a thoroughly vetted and recognized asset class, Bitcoin is on the verge of widespread institutional adoption.
With the approval of a Bitcoin spot ETF , demand for “Bitcoin-native” trading and income products is expected to surge, driven by their security and tax efficiency. This burgeoning interest may lead to the development of a variety of regulated Bitcoin-based financial products. By recognizing this shift, traditional banks may begin to integrate Bitcoin and these new products with their private blockchains, making them available to institutional clients at scale.
The importance of institutional integration into the Bitcoin DeFi ecosystem goes beyond capital injections. It represents the creation of a unique synergy, blending the advantages of traditional finance with the revolutionary aspects of decentralized financial systems. This convergence, built on the security and transparency of Bitcoin, will redefine the landscape of institutional finance and blur the lines between traditional and modern financial systems.
The end result of these developments—from cultural shifts to technological innovation and institutional adoption—will significantly drive Bitcoin’s market capitalization and total value locked in its ecosystem. As we navigate this version of the future of decentralized finance, it’s clear that Bitcoin is not just a digital asset, but the cornerstone of a new, trustless financial paradigm.
4. Summary
Evolving from a sleepy asset to a dynamic and foundational technology for decentralized finance, Bitcoin’s evolution is driven by its market cap of over $850 billion, underpinned by the stability and security of the network. However, a key challenge is the low utilization of Bitcoin network capabilities, which is caused by people often overlooking the difference between Bitcoin as a network and BTC as a digital asset. To activate this dormant capital and realize Bitcoin’s full potential, it is necessary to harness the power of the network to transform Bitcoin from a mere store of value into a core infrastructure within the Bitcoin economy.
This shift is reflected in the development of "layers" on top of the Bitcoin Core network (L1) to solve scalability issues, drawing on Ethereum's scalability and flexibility, while being driven by the introduction of Ordinal, which Marking a cultural and developmental shift. While major L1 upgrades like SegWit and Taproot have alleviated some of the issues, rising transaction fees highlight the growing need for more advanced L2 solutions like Stacks.
As we approach the 2024 halving event and the approval of a Bitcoin spot ETF , Bitcoin developments are shaping a more scalable and secure ecosystem. This evolution is expected to facilitate significant institutional adoption, placing Bitcoin at the forefront of a new financial paradigm that seamlessly integrates traditional and decentralized systems. Against the backdrop of Ordinal’s cultural impact and expanding use cases in DeFi and gaming, the potential of Bitcoin smart contracts is likely to attract growing interest and capital.
In the medium term, breakthroughs in Bitcoin L2 technology, especially the Nakamoto version of Stacks and the introduction of sBTC, promise to revolutionize the DeFi landscape. These developments are expected to bring a smoother, more efficient user experience and open up new possibilities for Bitcoin-based NFT markets and DeFi applications.
In the long term, the passage of a Bitcoin spot ETF will make Bitcoin a key player in institutional adoption of digital assets and DeFi . This event could trigger a massive shift in institutional investment toward Bitcoin-based financial products and services, enhancing synergies between traditional finance and decentralized financial systems. This integration is not just an injection of capital, but a fusion of the advantages of two worlds, opening up a new path for institutional finance.
Collectively, these developments are expected to significantly increase Bitcoin’s market capitalization and the total value locked in its ecosystem, opening a new chapter in the journey toward a DeFi future. Through innovations like Ordinal, the Nakamoto version, and Stacks’ sBTC, as well as institutional adoption following the approval of the Bitcoin Spot ETF, Bitcoin is not just maintaining its relevance, but is actively reshaping the future of finance as a new, trustless finance cornerstone of the paradigm.
Note: This article is a research report on the development of the Bitcoin ecosystem. The report was co-authored by The Spartan Group team, Kyle Ell1C0tt, and a number of experts who provided feedback and insights and generously gave their time to review the final version you are reading today. This section is the fourth in the final series of reports.
Source: https://medium.com/the-spartan-group/towards-a-trustless-financial-system-on-bitcoin-4-of-4-975d8a3c319f






