기관: KuCoin
1. 서론
많은 암호화폐 거래소들은 청산 위험을 방지하기 위해 복잡한 위험 관리 조치를 채택하고 있습니다. 이러한 조치에는 다단계 위험 한도 설정 및 높은 레버리지 사용 제한 등이 포함됩니다. 또한 거래소는 기초 자산의 가격과 시장 유동성에 따라 위험 한도와 마진 비율 등의 매개변수를 동적으로 조정합니다. 그러나 이러한 프로세스는 복잡할 뿐만 아니라 명확한 관리 기준이 부족하여, 내부적으로 일관성이 없는 시스템을 유지하는 데 많은 자원이 투입되어야 합니다. 예를 들어, 자금을 늘리더라도 레버리지 수준이 갑자기 변경될 수 있어 포지션 규모가 늘어나지 않을 수 있습니다.
일부 거래 플랫폼(그림 1 참조)에서는 거의 100개의 위험 한도 수준이 존재합니다. 이러한 수동적인 수준 변화는 시스템 관리의 복잡성을 높이고 강제 청산을 초래할 수 있어 사용자의 이익을 해칠 수 있습니다.
우리의 목표는 주어진 자금 하에서 합리적인 포지션 규모를 시뮬레이션할 수 있는 비선형 모델을 개발하여 더 유연하고 효율적인 위험 관리를 실현하는 것입니다. 이 방법은 내부 공식 체계를 재구축하여 일관성을 달성하고, 기존의 복잡한 위험 한도 템플릿에 대한 실용적인 대안을 제공합니다.
본 논문은 기존 한도 모델을 대체할 새로운 위험 관리 프레임워크를 제안합니다. 이 방법은 KuCoin의 교차 시스템에 구현되어 몇 가지 명확한 장점을 보여주었습니다:
1. 전통적인 거래소의 포지션 관리 설정에 더 가까워, 기관 자본이 더 쉽게 적응할 수 있습니다.
2. 포지션 규모 또는 레버리지 사용에 따른 위험 한도 조정이 필요하지 않습니다.
3. 운영 프로세스를 간소화하여 거래소의 부담을 줄이고, 거래소의 이익을 보호하기 위해 사용자의 이익을 해치는 위험을 낮출 수 있습니다.
이 모델은 위험 관리에 더 투명하고 간단한 방식을 제공하여 거래소 운영과 사용자 이익의 일치를 높입니다.
2. 모델
2.1 최대 포지션 규모
사용자 계정의 보유 자금을 C, 기초 자산의 선물 계약 가격을 p라고 가정합니다. 초기 마진 비율 r은 사용자가 선택한 레버리지의 역수에 해당합니다. 거래 수수료를 무시하면 사용자가 개설할 수 있는 계약 수는 다음과 같습니다:

그러나 자금 C가 너무 크거나 마진 비율 r이 너무 낮은 경우 거래소에 미치는 위험이 크게 증가합니다. 따라서 C와 r이 고정되고 C가 큰 경우, 거래소의 위험 등급 시스템은 허용되는 최대 포지션을 C/(p*r)보다 훨씬 낮은 수준으로 제한합니다. 반대로 C가 작은 경우 포지션 규모는 C/(p*r)에 더 가깝습니다.
많은 거래소는 이러한 관계를 관리하기 위해 수십 개에서 수백 개의 위험 등급을 사용합니다. 따라서 사용자 자금이 늘어남에 따라 사용자는 자신의 위험 등급을 조정해야 합니다. 이러한 제한은 다음과 같은 로그 함수로 대략 표현될 수 있습니다:
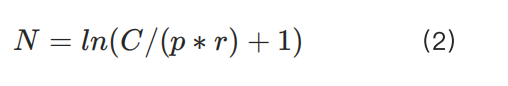
분명히 C가 큰 경우 로그 함수의 1차 도함수가 감소하여 실현 가능한 포지션 규모가 선형 공식 계산 결과보다 작아집니다. 그러나 이는 문제를 제기합니다: ln(x+1)≈x가 성립하려면 C가 충분히 작고 p가 충분히 커야 합니다. 그렇지 않으면 C가 작더라도 사용자가 이론적인 최대 포지션 C/(p*r)을 실현할 수 없습니다.
이 문제를 해결하기 위해 우리는 다른 계약 유형의 특성에 따라 더 큰 스케일링 파라미터 k를 도입하여 원래 공식을 수정했습니다:
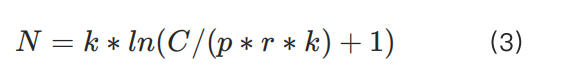
이 조정은 소액 자금 사용자의 요구를 충족시키면서도 대액 자금 사용자의 위험 통제 요구사항을 충족시킵니다.
KuCoin의 교차 시스템에서 우리는 이미 개설된 포지션과 기타 마진 요구사항을 고려하여 다음과 같은 변수를 정의했습니다:
• F: 기타 계약 및 미체결 주문이 점유하고 있는 마진.
• E: 사용자 선물 계정의 총 자본.
• Q: 새 주문 방향과 일치하는 보류 중인 주문의 포지션 규모.
• O: 현재 개설된 포지션 규모(새 주문 방향과 일치하면 양수, 그렇지 않으면 음수).
최대 허용 포지션 계산 공식은 다음과 같습니다:
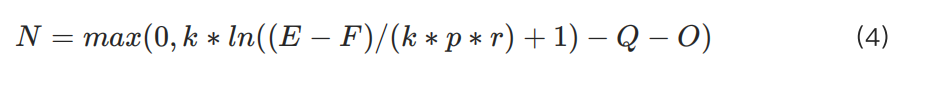
따라서 KuCoin의 이 모델에서 일반적인 자금 규모에 대한 레버리지와 최대 허용 포지션의 관계는 다음 그래프와 같이 표현될 수 있습니다:
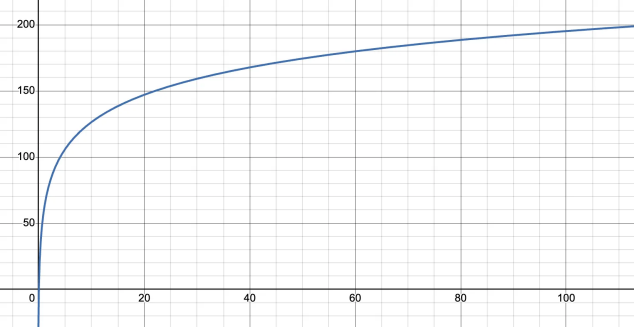
이 그래프는 비선형 마진 조정을 통해 규모와 안정성의 균형을 달성하는 방식을 보여줍니다. 즉, 소액 사용자의 최대 포지션 요구를 충족시키면서도 대액 사용자의 위험 통제를 보장합니다.
그러나 대부분의 거래소(예: OKX, Binance)에서 레버리지와 포지션 규모의 관계는 일반적으로 왜곡된 곡선으로 나타납니다:
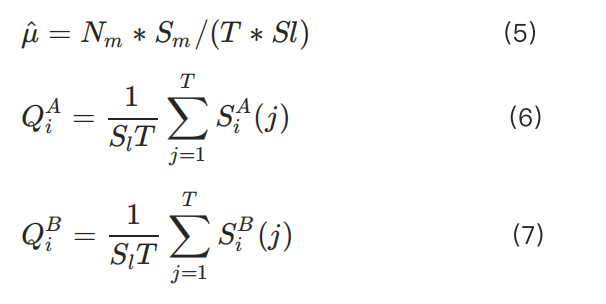
사실 유지 마진 비율(MMR)도 유사한 패턴을 보입니다. 이는 대액 자금 사용자에게 특히 도전적입니다. 예를 들어 초기 마진 비율(IMR)이 50%로 설정된 경우 MMR이 48%까지 높아질 수 있습니다. 이 경우 대규모 포지션을 시도하는 사용자는 낮은 레버리지만 사용해야 하지만 MMR은 비합리적으로 증가합니다.
이러한 설정은 사용자가 자금을 효과적으로 활용할 수 있는 능력을 제한하며, 레버리지 수준의 급격한 변화로 인해 빈번한 조정이 필요해 유연성이 떨어집니다. 이는 위험 관리와 사용자 경험 간의 불균형을 초래하여 대액 투자자가 이러한 제한 하에서 효율적으로 운영하기 어렵게 만듭니다.
2.2 MMR 및 IMR
MMR(유지 마진 비율)은 주로 청산 위험 관리를 돕는 보상 메커니즘입니다. 본질적으로 MMR은 유동성 추출 압력을 반영하며 미결제 포지션의 변화에 따라 동적으로 조정되어야 합니다. 다음은 거래소에서 접근할 수 있는 유동성 관련 지표를 기반으로 도출된 MMR의 이론적 값입니다.
2.2.1 유동성 관련 변수
유동성을 정확하게 평가하고 결정하기 위해 다음과 같은 변수를 식별했습니다. 이러한 변수는 일반적으로 거래소에서 관찰할 수 있습니다:
• μ: 시장 주문 실행 속도
• T: 청산 또는 거래소가 필요로 하는 시간
• i: 최선의 매수 또는 매도 가격과의 거리(가격 수준)
• j: 호가 시간 단위
• Qi: 주문 장부 거리 i에 있는 평균 주문 수량
• S: 주문의 평균 규모(시장 주문의 경우 , 지정가 주문의 경우 )
• N: 주문 수(시장 주문의 경우 , 취소 주문의 경우 , 지정가 주문의 경우 )
이러한 값은 안정된 시장 상황에서의 평균 상황을 나타냅니다.
2.2.2 사용자 포지션 지표 정의
• position: 모든 사용자의 순간 평균 포지션 규모, 거래소의 과거 데이터에서 얻을 수 있습니다.
• pos: 개별 사용자가 보유한 포지션 규모.
• X: MMR 범위 내에서 거래된 거래량의 합계.
• MMRup: MMR의 상한.
• rMMR: MMR의 최종값.
• R: 최선의 매수 또는 매도 가격과의 실제 거리, i와 j에 따라 달라집니다.
2.2.3 주문 흐름에 따른 MMR 조정
지정가 주문의 진입 및 취소 속도는 여러 수준의 평균값에 포함됩니다. 시장 주문은 즉시 실행될 가능성이 더 높으므로 증가 또는 감소를 고려해야 합니다. 다음과 같은 관계식이 이러한 동적 변화를 정의합니다:
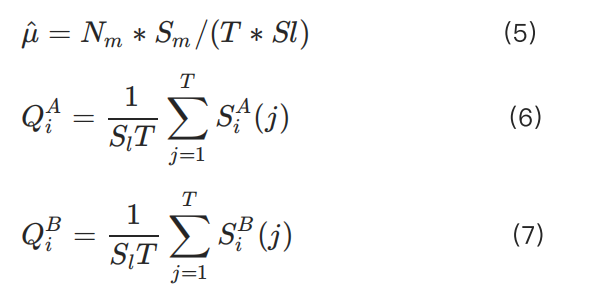
예를 들어 롱 포지션의 경우 강력한 청산 유동성은 매수 주문 수량(Q)일 수 있습니다:
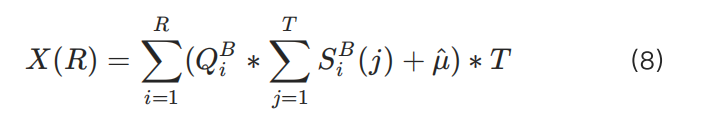
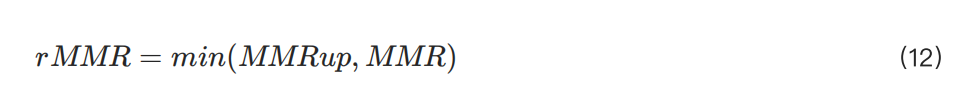
위의 방정식에서 볼 수 있듯이 R을 제외한 다른 변수들, 즉 포지션, Q, S, T 등은 이미 확정되어 있습니다. 따라서 이러한 변수들로부터 MMR과 rMMR을 계산할 수 있습니다.
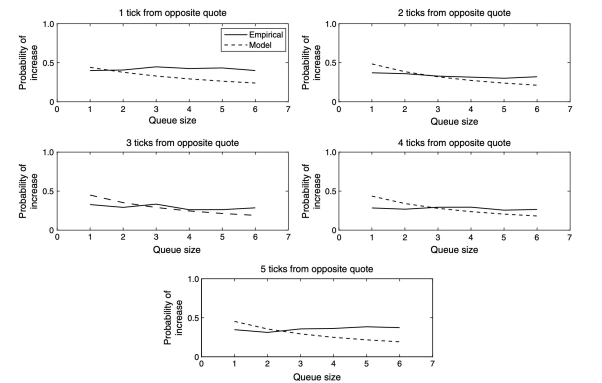
또한 MMRup의 상한선을 설정해야 합니다. 모델은 종종 보수적으로 추정하여 주요 가격 수준과 매수/매도 주문의 중요한 레벨이 오더북에 미치는 긍정적인 영향을 무시하기 때문입니다. CME의 일부 연구(그림 2 참조)는 이러한 영향을 더 정확하게 보여줍니다.
IMR(초기 보증금률)은 일반적으로 기초 자산의 레버리지와 유동성과 관련이 있으므로, 포지션 규모 등의 요인에 따라 동적으로 조정되어야 합니다. 다음과 같이 정의할 수 있습니다:
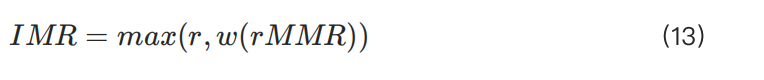
여기서 IMR은 2.1절에서 언급한 초기 보증금률 r에 해당합니다. w(rMMR) 함수는 더 큰 유연성을 제공합니다. 예를 들어, 거래소가 유동성이 비교적 안정적이라고 판단하는 경우 단순한 조정 방식, 즉 w(rMMR)=1.3×rMMR을 사용할 수 있습니다.
이러한 방법은 IMR이 현재 시장 상황과 유동성 수준을 반영하도록 보증금률을 동적으로 조정할 수 있는 실용적인 방법을 제공합니다. 고정된 보증금 규칙과 비교하면 이 시스템은 더 적응성이 있으며, 효과적인 리스크 관리를 통해 사용자와 거래소 모두에게 혜택을 줍니다.
3 근사 해 k
매개변수 k는 각 특정 자산(거래쌍)에 대해 설정된 전역 매개변수로, 기존 주문 또는 미결제 포지션을 고려할 필요가 없습니다. 원칙적으로 k 값이 클수록 사용자가 더 많은 포지션을 열 수 있습니다. 그러나 여기에는 중요한 제한이 있습니다: 허용되는 최대 포지션에 필요한 보증금이 총 자본에 IMR을 곱한 값을 초과할 수 없습니다.
단순화를 위해 허용되는 최대 포지션 공식을 변수 로 할당합니다:
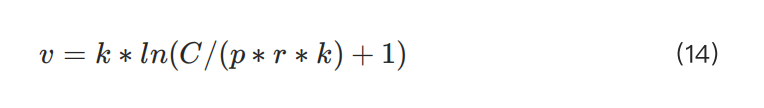
실제 레버리지는 사용된 보증금의 역수보다 작거나 같아야 합니다:
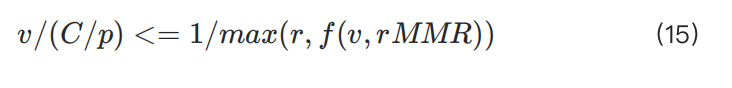
계산을 단순화하기 위해 새로운 변수 y를 도입하여 C(자본)와 p(가격)를 대체합니다:

결과는 다음과 같습니다:
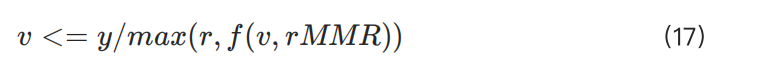
작은 포지션을 제외하면, 간단한 조정 1.3 × rMMR(f(pos,rMMR) 사용)이 일반적으로 r보다 작습니다. 작은 포지션의 경우 필요한 보증금이 무시할 수 있을 만큼 작아지므로, 이러한 상황은 우리의 리스크 모델에서 고려하지 않습니다. 마찬가지로 MMRup가 상한을 설정하므로 이 문맥에서도 무시할 수 있습니다.
따라서 우리는 1/IMR의 최소 가능 값만 고려하면 됩니다. 이 부등식은 다음과 같이 간단해질 수 있습니다:
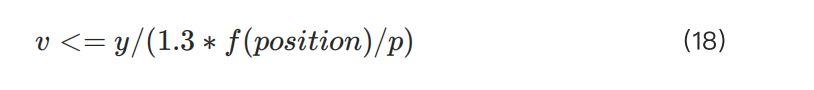
이 부등식은 최대 허용 포지션과 실제 레버리지 간의 관계를 보여줍니다.
다른 변수와 달리 포지션과 R은 명확한 반비례 관계를 가집니다. 따라서 R에서 유도된 MMR도 포지션과 반비례 관계를 가지며 다음과 같이 표현할 수 있습니다:

낮은 포지션 조건에서 MMR이 전통적인 형태(레버리지의 역수의 절반)를 따른다고 가정하면, 공식은 다음과 같이 작성할 수 있습니다:
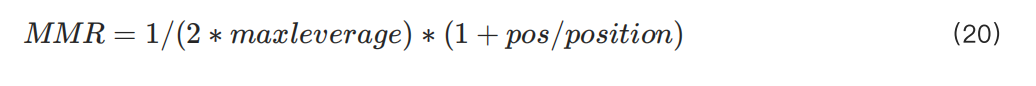
이 경우 k의 한계값을 찾으려고 하면 공식 (3)의 r이 1/maxleverage로 변경됩니다.
변수를 대체하면 부등식 (18)은 다음과 같이 변형됩니다:
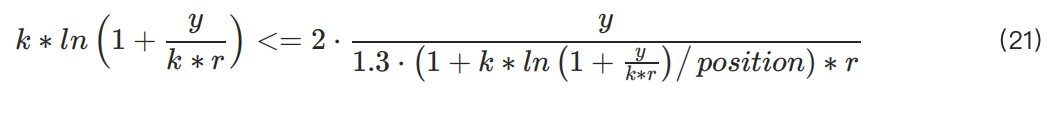
y(사용자 자본에 의해 결정)는 이론적으로 k 값에 영향을 미치지 않는다는 것을 관찰할 수 있습니다. 따라서 k는 주로 포지션에 의존합니다. k의 최소값은 y에 따라 변경되지만, 모든 상황에서의 최소 가능 값을 찾는 것이 목표이므로, 어떤 시나리오에서도 안전하게 포지션을 열 수 있습니다.
여기서 y/(k*r)은 여전히 하나의 변수로 대체할 수 있지만, 방정식은 여전히 복잡하여 해석적 해를 찾기 어렵습니다. 많은 근사 실험과 반복 시뮬레이션 끝에 k는 매우 간단한 표현식으로 수렴하는 것으로 발견되었습니다(k의 계산은 복잡하므로 여기서는 자세히 설명하지 않습니다):
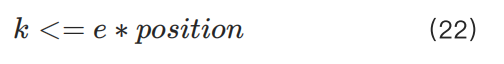
k 또는 포지션 값을 조정하여 자본 규모나 미결제 포지션 수가 크지 않은 경우 사용자가 C/(p*r)까지 포지션을 열 수 있습니다. 그렇지 않으면 제한을 받게 됩니다. 규모와 제한 수준은 k와 포지션에 의해 공동으로 제어됩니다. 따라서 다른 암호화폐에는 서로 다른 k 값이 적용됩니다.
4 결론
이상은 쿠코인의 교차 리스크 한도 시스템에 대한 간략한 소개입니다. 이 설계의 장점과 사용자 친화성은 명확합니다. 쿠코인의 교차 시스템에서는 리스크 한도 외에도 리스크 비율과 주문 보증금 사용이 태그 가격을 통해 동적으로 관리됩니다. 이러한 동적 관리는 사용자의 보증금을 최대한 활용할 뿐만 아니라 새로운 리스크 한도 프레임워크와 seamless하게 통합되어 시스템 효율성과 사용자 경험을 높입니다.
5 부록
그림 1:
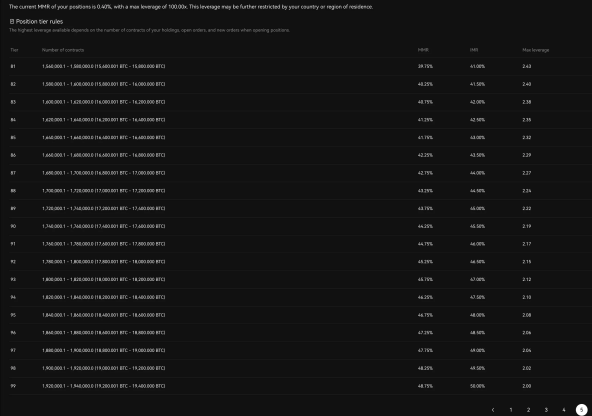
그림 2:
6 참고문헌
1. Rama Cont, Sasha Stoikov 및 Rishi Talreja, "A Stochastic Model for Order Book Dynamics", Operations Research, 2010년, 제58권 제3호, 549-563페이지.
2. "Forecasting Initial Margin Requirements — A Model Evaluation", Journal of Financial Markets, 제40권, 2018년.
3. Alfonsi, A., A. Schied, A. Schulz, "Optimal execution strategies in limit order books with general shape functions", Quant. Finance, 2010년, 제10권 제2호, 143-157페이지.