익명 참여에 대한 인센티브 제공에 관하여

익명 참여에 대한 인센티브 제공에 관하여

upload_0bca3fb7f6b0d2fc3fe0596f28531112 1300×867 189KB

\c점 ⋅
요약: 블록체인 활동은 공유 프로토콜에 참여하는 독립적인 행위자를 통해 촉진됩니다. 이러한 참여에 대한 인센티브를 제공하는 것은 특히 허가가 없고 적대적이며 익명성이 보장되는 환경에서 중요한 설계 고려 사항입니다. 섹션 1 에서는 모델을 제시하고 참여 게임에 대한 동기를 부여합니다. 섹션 2 에서는 이 게임의 대칭적이고 익명적인 평형을 분석합니다. 그런 다음 이 프레임워크를 두 가지 설정에 적용합니다. 섹션 3에서는 최소한 하나의 증명 생성에 인센티브를 제공하는 것을 목표로 하는 증명자 시장에 대해 자세히 설명합니다. 섹션 4 에서는 최소 50%의 참여 에 인센티브를 제공하는 것을 목표로 하는 작업 증명 프로토콜을 살펴봅니다(51% 공격을 방지하는 목표에 의해 동기 부여됨). 두 경우 모두 프로토콜의 비용을 최소화하기 위한 최적의 인센티브 구조를 도출합니다. 섹션 5 에서는 모델을 확장하는 방법과 참여 부트스트래핑에 사용되는 기타 블록체인별 기술을 논의하여 결론을 내립니다.
\c점 ⋅
작성자: maryam & mike – 2025년 5월 26일.
\c점 ⋅
이 게시물에 대한 리뷰와 토론에 참여해주신 Akilesh , Noam , Matt , Barnabé 에게 감사드립니다!

내용물

(1) 동기 및 모델
(1.1). 참여 게임 모델
(1.2). 익명이 아닌 간단한 솔루션
(1.3). 비대칭 평형
(2) 복권지급규칙의 대칭평형
(2.1). 큰 n n을 고려하면
(3) 프로버 시장 비용 최소화
(3.1). 최소 한 명의 참가자를 위한 최적화
(3.2). 점근선
(3.3). 1 + \ln c 1 + ln c 바운드는 꽉 조여져 있다
(4). 작업 증명 목적 함수
(4.1). 점근선
(5) 결론 및 향후 연구
(5.1). 대체 비용 함수
(5.2). 이기종 에이전트와 정보 비대칭성
(5.3). 토큰, 에어드랍 및 블록체인 애플리케이션

1. 동기 및 모델

오프닝 비네트 – 동네 스포츠 바에 앉아 NBA 플레이오프 경기를 관람하려고 합니다. 혼자 보기는 싫어서 그룹 채팅방에 당신이 왔다는 것을 알리려고 합니다. 사람들이 더 많이 오도록 하기 위해 윙을 먼저 사겠다고 제안하지만, 먼저 얼마나 주문할지 결정해야 합니다. 너무 적게 주문하면 다른 사람이 갈 거라고 생각해서 아무도 오지 않을 가능성이 있습니다. 너무 많이 주문하면 모두가 오면 테이블에 자리가 없을 것입니다. 친구 중 일부만 오도록 하려면 윙을 얼마나 사는 것이 가장 좋을까요? ¹

이 이야기는 블록체인 프로토콜 설계에서 자주 언급됩니다. 프로토콜은 어떤 형태로든 참여를 유도하고 이를 위해 인센티브를 활용하고자 합니다.

• 작업 증명은 채굴자들이 암호화 퍼즐을 풀도록 유도하기 위해 블록 보상을 제공합니다.
• 지분 증명 방식은 블록에 대한 올바른 지분 스테이킹과 투표에 대해 합의 보상을 제공합니다.
• 증명 시장은 계산 집약적인 ZK 증명의 생산을 조정합니다.

결정적으로, 블록체인은 허가 없이도 참여를 허용하고자 합니다. 이는 조정 문제를 훨씬 더 어렵게 만듭니다. 이 글에서는 참여를 유도하는 모델을 제시하고 익명의 공통 가치 지불 규칙의 대칭적 균형을 분석합니다. 특히, 각 플레이어가 확률 pp 로 복권을 구매하는 혼합 전략을 사용하는 균형을 연구합니다.

1.1. 참여 게임 모델

참여 게임은 다음과 같이 모델링됩니다.

• 플레이어 – 플레이어는 메커니즘을 기반으로 입장권 구매를 선택할 수 있는 전략적 행위자입니다.
• 참가자 – 참가자는 입장권을 구매하는 플레이어입니다.
• 프로토콜 – 프로토콜은 참여를 유도하기 위한 비용 함수(또는 동등하게 양의 평가 함수)를 갖춘 에이전트입니다.
• 지불 규칙 – 프로토콜에 의해 구현된 기능으로 참가자 집합을 해당 지불에 매핑합니다.

참여 게임에 n n 명의 플레이어가 있다고 가정합니다. 각 플레이어는 동일한 참가비 q q 를 받게 되므로 이는 공통 가치 경매입니다. 단순화를 위해 이 글의 나머지 부분에서는 q = 1 q = 1 로 사용합니다. 각 참가자는 참여 여부를 결정적으로 결정할 수 있습니다. 또한 확률 p p 로 참여하는 무작위 전략을 선택할 수도 있습니다. 참여 여부를 결정하기 전에 참가자는 프로토콜에서 지정한 지불 규칙을 따릅니다. 지불 규칙은 실현된 참가자 세트에 따라 달라질 수 있으며 무작위로 지정될 수 있습니다. 각 참가자는 기대 효용을 극대화하는 행동을 선택합니다. 즉, 예상되는 지불금에서 참가비를 뺀 값(참여하기로 선택한 경우)을 의미합니다.

다음 두 섹션에서는 익명성과 대칭성의 개념을 소개합니다.

1.2. 사소하고 익명이 아닌 솔루션

프로토콜이 최소 한 명의 참가자를 유치하는 것을 목표로 하고, 참여를 선호하는 플레이어들이 동점 상황에서 벗어나도록 가정한다고 가정해 보겠습니다. 간단한 메커니즘은 다음과 같습니다. " WINNER 라고 표시된 특정 플레이어를 선택하고, 참여하면 1달러를 지급하겠다고 말합니다." 이 간단한 해결책은 다음과 같은 여러 가지 바람직한 특성을 가지고 있습니다.

1. 모든 사람을 위한 개별 합리성 (각 플레이어가 참여하지 않으면 유틸리티가 0이 될 수 있기 때문)
2. 균형 상태에서 만족스러운 참여 ( WINNER 참여하고 다른 사람은 참여하지 않음)
3. 프로토콜에 대한 지불 최소화 (티켓 수수료가 1달러이므로 참가자를 모집하는 데 드는 비용이 가장 적기 때문).

프로토콜 설계자가 승자를 선택하는 데 동의한다면 이 솔루션은 충분합니다. ² 여기서 멈추지 않고 익명의 솔루션 세트에 집중합니다.

정의(비공식): 익명의 지불 규칙은 플레이어의 신원에 따라 달라질 수 없습니다.

이 속성은 3.3절 에서 공식화하지만, 직관적으로 이해하기 쉽도록 구현되어 있습니다. 이러한 지급 규칙은 모든 플레이어를 동등하게 대우 해야 합니다 . 규칙은 플레이어의 행동에 따라 달라질 수 있으며(예: 참가하는 모든 참가자에게 상금을 균등하게 분배), 무작위로 설정될 수도 있습니다(예: 한 명의 참가자에게 무작위로 상금을 지급). 그러나 위의 메커니즘은 플레이어의 신원에 의존하며 익명성을 보장하지 않습니다.

1.3. 비대칭 평형

별도로 다음 시나리오를 고려해 보겠습니다. " COMMITTER 로 표시된 한 명의 플레이어가 티켓을 구매하고 참여자가 되기로 공개적으로 약속합니다." 지불 규칙에 따라 이 약속은 다른 플레이어가 참여하는 것을 억제할 수 있습니다. 예를 들어 지불 규칙이 모든 참여자에게 1달러의 상금을 균등하게 분배한다고 가정해 보겠습니다. 이 경우 참여를 고려하는 두 번째 플레이어는 1달러를 지불하고 1/2달러를 얻기 때문에 음의 효용이 보장됩니다. 이로 인해 다른 아무도 프로토콜에 참여하지 않고 COMMITTER 전체 상금을 얻습니다. 이 균형은 프로토콜에 대한 지불을 최소화 하지만 참여자가 COMMITTER 선택해야 하므로 조정 복잡성이 플레이어에게 전가됩니다. 이 예를 동기로 사용하여 대칭 균형 에 대한 관심을 제한합니다.

정의: 대칭적 평형 상태에서는 각 플레이어가 동일한 전략을 사용합니다.

이 전략은 결정론적(예: 항상 티켓을 구매하고 참여)이거나 혼합형(예: 확률 p p 로 티켓을 구매)일 수 있습니다. 이러한 결정론적 전략은 각각 p=0 p = 0 또는 p=1 p = 1 로 생각할 수 있으므로 모든 대칭 평형은 단일 값 p\in[0,1] p ∈ [ 0 , 1 ] 에 의해 완전히 지정됩니다. 이러한 평형에서 참가자 수는 \text{Binomial}(n,p) Binomial ( n , p ) 에서 도출되며, 여기서 n n 은 플레이어 수입니다.

2. 복권 지급 규칙의 대칭적 균형

우리의 관심이 대칭적 평형에만 국한되어 있기 때문에 플레이어의 전략에 대한 결과는 세 가지뿐입니다.

1. 아무도 참여하지 않음( p=0 p = 0 ),
2. 모두가 참여합니다( p=1 p = 1 ),
3. 모두가 확률 p\in (0,1) p ∈ ( 0 , 1 ) 로 참여합니다.

지급 규칙에 따라 이러한 결과가 모두 가능합니다. 이 섹션에서는 복권 지급 규칙을 살펴봅니다.

정의: 복권 지급 규칙은 참가자 집단에서 균일하게 무작위로 당첨자를 선정하여 한 명의 플레이어에게 x x 크기의 상금을 지급합니다.

복권 지급 규칙은 익명이며 x x 의 크기에 따라 대칭적 평형 p p 를 유도합니다. 프로토콜은 x x 의 값을 설정하고, 플레이어는 참여할지 여부를 결정하며, 상금은 참가자 중 한 명에게 전액 지급됩니다. x < 1 x < 1 이면 (1)의 경우입니다. 상금이 참가비보다 적기 때문에 아무도 참여하지 않습니다. x\geq n x ≥ n 이면 (2)의 경우입니다. 모두가 참가비보다 더 많은 돈을 받을 것이라는 보장(기대)이 있기 때문에 참여합니다. x x 의 다른 값에 대해 참가자 수는 \text{Binomial}(n,p) Binomial ( n , p ) 에서 추출한 임의 변수가 됩니다. 여기서 p\in (0,1) p ∈ ( 0 , 1 ) 입니다 . 프로토콜은 x x 를 조정하여 평균 np n p 를 이동할 수 있습니다.

각 플레이어가 자신의 전략을 혼합하고 확률 p p 로 결합하는 위 사례 (3)에서 대칭적 균형을 특성화할 수 있습니다. (이에 대한 여러 가지 접근 방식이 있지만, 여기서는 미분을 사용하여 명시적인 접근 방식을 보여줍니다. 대안은 별책 #1을 참조하십시오.) 플레이어 i i 의 결정을 다른 플레이어들의 전략을 p p 로 고정하는 것으로 고려합니다. i i 는 기대 효용을 극대화하기 위해 결합 확률 p' p ′ 을 선택합니다.

즉, 플레이어 i i는 참여자 중 복권에 당첨되어 참여하면 x x 의 지불금을 받습니다.특히, 다른 n-1명의 n − 1명의 플레이어는 각각 확률 p p 로 독립적으로 참여하므로 i i를 제외한 참여자 수는 \text{Binomial}(n-1,p) Binomial ( n − 1 , p ) 에서 추출됩니다.i i 가 참여함으로써 얻는 효용은 지불금에서 티켓 가격을 뺀 값입니다.i i 가 확률 p' p ′ 로 참여함으로써 얻는 효용은 참여함으로써 얻는 효용에 p' p ′ 를 곱한 값입니다.왜냐하면 i i 는 참여하지 않음으로써 얻는 효용이 0이기 때문입니다.

대칭 전략 p p가 평형이 되려면 p'=p p ′ = p가 모든 p'\in[0,1] p ′ ∈ [ 0 , 1 ] 중에서 이 표현식을 최대화해야 합니다. 1차 조건은 다음과 같습니다.

이것을 0으로 설정하면 x x 와 p p 사이의 관계에 대한 분석적 솔루션을 얻습니다.

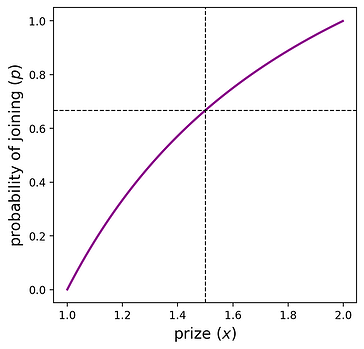
이것은 "크기 x 의 상이 주어졌을 때 대칭적 평형을 만드는 확률 p p는 무엇인가" 또는 동등하게 "프로토콜 설계자가 참가자 수가 \text{Binomial}(n,p) Binomial ( n , p ) 에서 나오기를 원한다면 크기 x x 의 상금을 설정한다"는 것을 알려줍니다. 아래 플롯은 n=2 n = 2 에 대한 이러한 변수 간의 관계를 보여줍니다.

upload_d625b6de301ed0283341dc168f71222a 931×895 37.7KB

점선은 "프로토콜이 상금을 x=1.5 x = 1.5 로 설정하면 전략 p=2/3 p = 2 / 3 은 대칭적 평형"으로 해석됩니다. 또한 상금이 <1 < 1 또는 >2 > 2 인 경우 플레이어는 각각 0 또는 1의 확률로 참여합니다. 이는 이 섹션의 시작 부분에서 설명한 "아무도 참여하지 않음"과 "모두 참여함" 결과입니다. 내부 영역 x \in (1,2) x ∈ ( 1 , 2 ) 의 경우 각 x x 에 의해 고유한 p p가 유도됩니다.

#1을 제외하고 동일한 방정식을 도출하는 다른 방법은 모든 플레이어 집합의 총 현금 흐름을 고려하는 것입니다. 주어진 p p 에 대해 플레이어 집합은 예상 참가비로 np n p 를 지불합니다. 따라서 프로토콜은 상환으로 기대치로 np n p 를 지불해야 합니다(이는 경쟁적 균형이기 때문에 초과 가치는 경쟁으로 인해 사라집니다). 프로토콜이 상금 x x 를 선택하면 플레이어 집합은 최소한 한 명의 플레이어가 참여하는 한 이 상을 받습니다. 이는 확률 1-(1-p)^n 1 − ( 1 − p ) n 으로 발생하며, 이는 플레이어 집합이 보상으로 x \cdot (1-(1-p)^n) x ⋅ ( 1 − ( 1 − p ) n ) 을 얻는다는 것을 의미합니다.

2번 여담: 혼합 전략 균형의 흥미로운 특성 중 하나는 플레이어가 두 행동 모두에 무차별하다는 것입니다(이것이 바로 플레이어가 애초에 자신의 행동을 무작위로 선택하는 이유입니다). 위의 예에서, 다른 모든 사람이 확률 p p 로 참여한다면, 플레이어 i 는 어떤 행동에서도 효용을 얻지 못합니다. x x 를 플레이어의 효용 함수에 대입하면 이를 알 수 있습니다.

\begin{align}U_i(p') &= \bigg[ x \cdot \frac{1-(1-p)^n}{np} -1\bigg] \cdot p' \\&= \bigg[\frac{np}{1-(1-p)^n}\cdot \frac{1-(1-p)^n}{np} -1\bigg] p' \\&= (1-1)p'\\&= 0.\end{align}

[수학 처리 오류]

이를 해석하는 또 다른 방법은 균형이 완전 경쟁적이라는 것입니다. 이는 결과와 그 결과로 나타나는 혼합 전략 사이에 무차별성을 유도합니다.

2.1 큰 n n을 고려

관계를 회상하다

이 방정식에 대한 흥미로운 관찰은 큰 n n 에 대해 x x 를 \mu=np μ = n p (예상 참가자 수)의 함수로 다시 쓸 수 있다는 것입니다. 작은 x x 에 대해 (1-x) \rightarrow e^{-x} ( 1 − x ) → e − x 를 사용합니다.

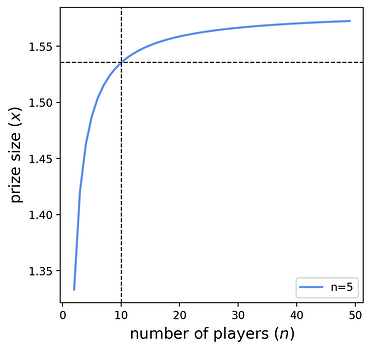
이 간단한 공식을 사용하여 프로토콜은 n n 을 알지 않고도 원하는 평균 참여 수 \mu μ 를 목표로 할 수 있습니다. 예를 들어, 프로토콜이 기대되는 단일 참여자를 원하는 경우 1/(1-1/e)\approx 1.582 1 / ( 1 − 1 / e ) ≈ 1.582 의 상금을 설정해야 합니다. 즉, 프로토콜은 기대되는 한 명의 참여자를 유치하기 위해 1 1 의 참가비에 58\% 58 % 프리미엄을 지불합니다. 이 근사치는 n n 이 커질수록 향상됩니다. 아래 플롯은 평균적으로 한 명의 참여자를 유치하는 데 필요한 프로토콜 상금을 보여줍니다. 또한 n \to \infty n → ∞ 가 x(1)=1/(1-1/e) x ( 1 ) = 1 / ( 1 − 1 / e ) 에 가까워짐에 따라 한계가 표시됩니다.

upload_9cde4a87098e4108fb332832c204d531 949×895 33.3KB

점선은 다음과 같이 해석할 수 있습니다. " n=10 n = 10 이면, 프로토콜 설계자는 한 명의 참가자를 기대치에 따라 유치하기 위해 최소 x=1.535 x = 1.535 의 상금을 설정해야 합니다." 물론, 프로토콜 설계자는 참가자가 없을 위험을 줄이기 위해 더 높은 상금을 선택할 수도 있습니다. 다음 섹션에서는 이러한 상충 관계를 공식적으로 설명합니다.

3. 프로버 시장 비용 최소화

지금까지 프로토콜이 x x 를 변화시켜 특정 예상 참여 횟수( \mu μ )를 어떻게 목표로 삼을 수 있는지 살펴보았습니다. 이제 낮은 참여율을 특히 싫어하는 프로토콜들을 고려해 보겠습니다. "낮은 참여 페널티"를 도입하여 이를 공식화합니다. 이 섹션에서는 증명자 시장을 살펴보는 것으로 시작합니다. 섹션 4 에서는 작업 증명 합의에 의해 유발되는 다른 낮은 참여 페널티를 살펴보겠습니다.

값비싼 증명 생성에 인센티브를 부여하고자 하는 ZK 롤업을 고려해 보겠습니다. 시장 설계자는 최소 한 명의 증명자가 참여하는 것(그리고 증명 생성 비용인 참여 수수료를 지불하는 것)에만 관심이 있을 수 있습니다. ^3. 또한, 참여자가 전혀 없다면 프로토콜은 c c 의 비용으로 증명을 직접 생성할 수 있습니다( c c 는 "외부 옵션"으로 생각할 수 있습니다). 이를 통해 참여자 수 k k 의 함수로 낮은 참여 페널티를 다음과 같이 표현할 수 있습니다.

당연히 프로토콜 설계자는 총 비용(상금 규모와 페널티)을 최소화하는 지불 규칙을 선택하고자 합니다.

3.1. 최소 한 명의 참가자를 위한 최적화

위 분석을 통해 프로토콜 설계자는 x x 와 p p 사이의 관계에 의해 유도된 대칭적 균형 하에서 특정 참여율을 목표로 상금 규모를 선택할 수 있습니다. 참여 페널티가 낮을 경우, 프로토콜의 비용 함수는 C_p C p 로 표시되며, 다음과 같습니다.

이 비용은 프로토콜이 최소화하려는 것이며, 프로토콜은 c c 가 주어졌을 때 x x 를 선택할 때 상충 관계에 직면합니다. x x 값이 너무 낮으면 프로토콜은 높은 확률로 c c 의 페널티를 받게 됩니다. x x 값이 높으면 프로토콜이 더 큰 보상을 지불해야 하므로 직접적으로 비용이 발생합니다. 대칭 균형에서 각 참가자가 p p 의 확률로 참여한다는 사실을 이용하면 다음과 같이 쓸 수 있습니다.

x = \frac{np}{1-(1-p)^n} x = n p 1 − ( 1 − p ) n (위에서 도출한 관계)는 다음과 같이 단순화됩니다.

이는 프로토콜 비용으로, p \in [0,1] p ∈ [ 0 , 1 ] 에 대해 최소화하려고 합니다. 최적 확률 p^* p ∗ 를 사용하면 프로토콜은 p^* p ∗ 에서 대칭 평형을 유도하는 데 필요한 상금 크기를 직접 계산할 수 있습니다. 1차 조건을 사용하여 프로토콜의 비용을 최소화합니다.

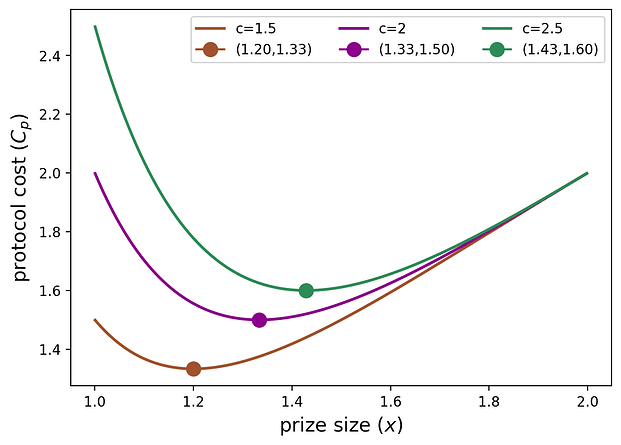
2차 미분은 항상 p \in [0,1] p ∈ [ 0 , 1 ] 에 대해 음수이므로 p^* p ∗ 는 실제로 프로토콜 비용의 고유한 국소 최소화자입니다. 다음 플롯은 프로토콜 비용을 x x 의 함수로 보여줍니다(각각 n=2 n = 2 및 c=1.5,2,2.5 c = 1.5 , 2 , 2.5 에 대해 p\in(0,1) p ∈ ( 0 , 1 ) 인 일대일 대응).

upload_68cf7e34e09faa5dfee6d7ce96b8e0fb 1246×895 62.3KB

x^* x ∗ 값(플롯에서 점으로 표시)은 c c 단위 로 증가합니다. 이는 프로토콜이 미참여 시 더 큰 페널티를 받게 되므로, 최소 한 명의 플레이어가 참여할 것이라는 확신을 높이기 위해 더 높은 x^* x ∗ 값을 선택하기 때문입니다(이는 더 높은 p^* p ∗ 값을 초래합니다). p^* p ∗ 값 으로부터 닫힌 형태로 최적의 상금 규모를 다음과 같이 계산합니다.

또한 우리는 최적의 프로토콜 비용을 계산합니다.

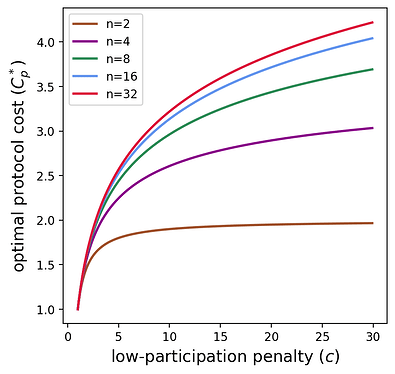
아래 그림은 이 비용을 n,c n , c 의 함수로 시각화하는 데 도움이 됩니다.

upload_32974a3ccb2b0fc03b6c63af46b5baa4 945×895 66.1KB

저참여 페널티가 증가함에 따라 프로토콜 비용은 대수적으로 증가하는 것으로 보입니다. 다음 섹션에서는 프로토콜 비용의 점근적 양상을 살펴보며 이러한 관계를 공식화합니다.

3.2 점근법

p^*, x^*, C_p^* p ∗ , x ∗ , C ∗ p 의 값이 c c 에 따라 어떻게 변하는지에 대한 자연스러운 의문이 제기됩니다. 특히, 프로토콜 설계자는 게임에 참여하는 플레이어 수 n n 이 많을 때, 프로토콜의 효용이 c c 에 따라 어떻게 변하는지 알고 싶어할 수 있습니다. 이를 확장하면(유도에 대한 각주 ⁴ 참조), 다음과 같은 식이 됩니다.

마찬가지로, 우리는 비용 최소화 프로토콜에 대한 최적의 보상인 x^* x ∗ 의 점근적 행동을 조사할 수 있습니다(유도에 대한 각주 ⁵ 참조).

마지막으로, 우리는 프로토콜이 지불하는 최적 비용 C_p^* C ∗ p 의 점근적 행동을 조사합니다(도출에 대한 각주 ⁶ 참조):

중요한 점은 n\to\infty n → ∞ 일 때 프로토콜의 총 비용이 1+ \ln c 1 + ln 으로 확장된다는 것입니다. c . 이는 외부 옵션의 함수로서 비용에 대한 대수적 경계를 제공하기 때문에 프로토콜에 매우 유용합니다. 또한, 최적 비용은 n n 에 의존하지 않습니다. 이는 권한이 없는 환경에서 유용합니다. 프로토콜은 플레이어 수를 알지 못해도 외부 옵션의 품질(즉, 참여도가 낮은 페널티)만을 기반으로 최적의 보상을 설정할 수 있기 때문입니다! 또한, 게임 참여자 수가 매우 많더라도 프로토콜은 비용이 제한되어 있음을 확신할 수 있습니다. ⁷

다음 섹션에서는 "이 대수 경계를 이길 수 있을까?"라는 질문에 답합니다. 더 공식적으로 말하면, 결과 대칭 평형이 프로토콜 비용 C_p < 1+\ln c C p < 1 + ln 을 갖도록 하는 익명 지불 규칙이 존재합니까? c ? 다음 섹션에서 답은 ' 아니요'임을 보여줍니다! 프로토콜 비용은 1+\ln c 1 + ln 으로 엄격하게 제한됩니다. 다 .

3.3 1+\ln c 1 + ln c 바운드는 꽉 조여져 있다

Note for the math/formalism-averse crowd: this section can be safely skipped!

각 플레이어가 대칭 평형에서 확률 p p 로 참여한다는 것을 알고 있습니다. 1.2절 에서 간략히 설명한 익명성 속성을 공식화하여 다른 익명 지불 규칙과 메커니즘을 비교해야 합니다. 지불 규칙 \pi(S,r) π ( S , r ) 은 참여한 참가자의 집합 S\subseteq [n] S ⊆ [ n ] 과 난수 시드 r r 을 입력으로 받고 각 참가자에게 지불을 출력합니다. 이전 절의 메커니즘은 S S 가 비어 있지 않고 그렇지 않으면 아무에게도 지불하지 않으면 확률 1/|S| 1 / | S | 로 무작위 참가자에게 복권 상금 x x 를 지불합니다. 메커니즘 \pi(S,r) π ( S , r ) 은 에이전트의 행동에 대해 점별 대칭인 경우 (사후) 익명이라고 합니다. 형식적으로, \pi π 는 모든 r r 및 S S 와 모든 순열 \sigma σ 에 대해 \pi(S,r)=\pi(\sigma(S),r) π ( S , r ) = π ( σ ( S ) , r ) 일 때 사후 익명 입니다 . 메커니즘 이 익명일 때 지불 규칙을 \pi(S,r)=\pi(k,r) π ( S , r ) = π ( k , r )로 다시 쓸 수 있습니다. 여기서 k=|S| k = | S | 이고 \text{Binom}(n,p) Binom ( n , p ) 에서 가져옵니다. 이제 특정 집합보다는 참여자의 수만 고려합니다.

π(k,r) π ( k , r ) 가 대칭 평형 p p를 갖는 익명 메커니즘이라고 하자. 그러면 경매인의 예상 비용은 다음과 같다.

이 기대값은 무작위성 실현 r r 과 각 가능한 참가자 수 k k 에 적용됩니다. 기대값에서, k k 명의 참가자 각자가 복권에 참여하기 위해 개별적으로 합리적이어야 함을 알 수 있습니다. 전체적으로, 모든 프로토콜은 기대값에서 최소한 각