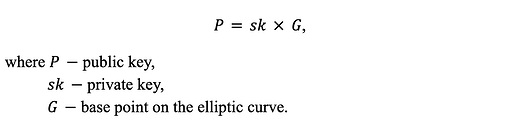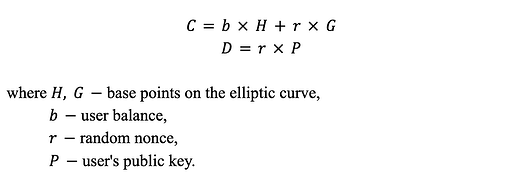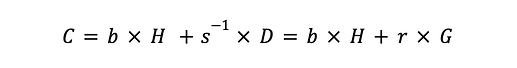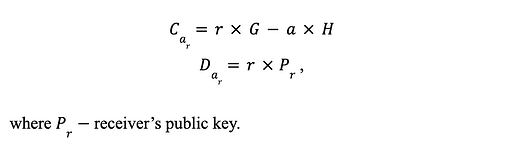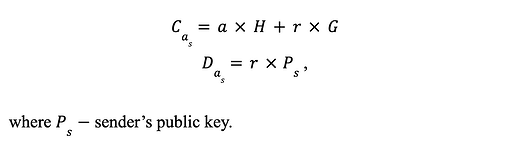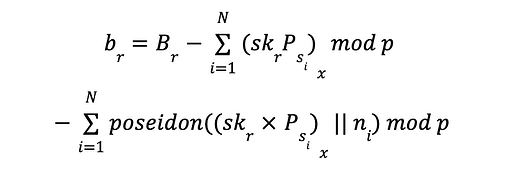개인정보 보호는 이더리움의 장기적 생존과 운영에 매우 중요합니다.

놀라운이더리움 프라이버시: 자기 주권으로 가는 길 로드맵에 따라, 우리는 기밀 WETH라는 개념을 생각해 냈는데, 이는 미래에 본격적인 기밀 토큰 표준(이더리움 개선 제안(EIP) )으로 성장할 수도 있습니다.

초안에 대한 여러분의 생각을 듣고 싶습니다!

1. 서론

투명성은 퍼블릭 블록체인의 주요 이점 중 하나입니다. 그러나 거래 내역이 공개적으로 공개되면 사용자의 프라이버시가 침해될 가능성이 있습니다. 근본적인 과제는 블록체인의 개방성이 제공하는 본질적인 이점과 개인의 기밀 유지라는 필수적인 요구 사이에서 균형을 맞추는 것입니다.

목표는 이더리움(ETH) 토큰 내 사용자의 금융 활동을 암호화하여 잔액과 이체 금액을 난독화하는 비허가형(Permissionless) 공익 프로토콜을 만드는 것입니다. 이를 통해 중앙화된 기관에 의존하지 않고도 이더리움(ETH) 를 이용한 기밀 P2P 결제, 기부 및 인수가 가능해집니다.

이 제안은 애플리케이션 계층 내에서 래핑된 이더리움(cWETH)의 기밀 버전을 생성하는 것을 제안합니다. 이 솔루션은 기밀성을 유지하기 위해 타원 곡선(EC) 트위스티드 엘가말(ElGamal) 기반 커밋 스킴(commitment scheme)과 커밋 스킴으로 인해 제한된 접근성을 제공하기 위해 EC 디피-헬만(DH) 프로토콜을 결합합니다. 올바른 커밋 생성, 암호화 및 복호화를 위해 zk-SNARK가 활용됩니다.

1.1. 기존 프로토콜과의 차이점

프로토콜 계층을 수정하지 않고 그대로 구현할 수 있는 알려진 솔루션이 두 가지 이상 있습니다.

솔라나(Solana) 와 Zether 접근 방식은 ElGamal 커밋을 사용하기 때문에 언뜻 보기에 매우 유사해 보일 수 있습니다. 그러나 가장 큰 차이점은 암호화된 잔액에 접근하기 위해 이산 대수 문제를 해결해야 한다는 것입니다.

솔라나(Solana) 별도의 복호화 가능한 잔액을 유지함으로써 이 문제를 부분적으로 완화합니다. 하지만 주요 차이점은 사용된 암호화 체계가 집계를 지원하지 않고, 이러한 잔액은 주로 캐시로 작동하며, 보류 중인 금액이 실제 금액으로 이동될 때 업데이트된다는 것입니다. 그러나 ElGamal 커미트먼트로 표현된 잔액을 디크립트(Decrypt) 해야 하므로 이산 대수 문제를 해결해야 할 필요성이 다시 제기됩니다. 값을 청크로 나누면 이 과정을 간소화할 수 있지만, cWETH 프로토콜은 집계 가능하고 ElGamal 커미트먼트와 함께 관리되는 암호화 체계를 제안하여 이산 대수 계산을 전혀 하지 않도록 합니다.

또 다른 차이점은 cWETH에서 사용하는 ZK 증명에 있습니다. 솔라나(Solana) 와 Zether 접근 방식 모두 Sigma 프로토콜과 방탄(bulletproof)에 의존하는 반면, 이 제안은 zk-SNARK를 기반으로 합니다. 이 제안의 단점은 신뢰할 수 있는 설정이 필요하다는 점인데, Plonk의 범용 설정과 같이 시간이 지남에 따라 안전함이 입증된 기존의 신뢰할 수 있는 설정을 사용하면 이러한 문제를 완화할 수 있습니다.

2. cWETH 개요

2.1. 이더리움(ETH) 래핑

기밀 계좌 설정 과정은 이더리움(ETH) 래핑 작업의 일부로 간주됩니다. 일반적인 래핑 로직과 함께, cWETH 컨트랙트에 첫 입금 시 각 사용자는 잔액 관리에 사용될 babyJubJub 공개 키를 제공합니다.

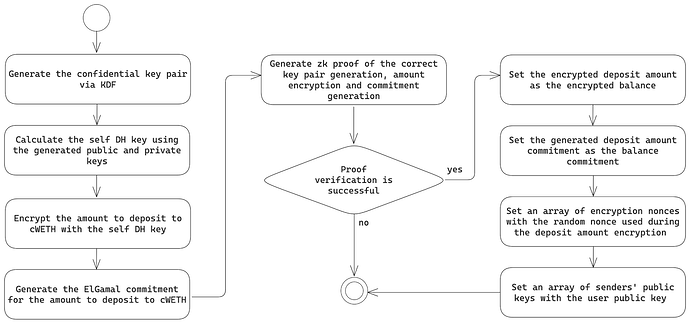
이 공개 키는 토큰 금액 및 잔액 계산의 커밋 및 암호화에 사용됩니다. 키 쌍 생성 및 초기 입금 흐름은 다음 다이어그램에 나와 있습니다.

그림 1: cWETH 흐름에 대한 초기 입금 1999×938 225KB

cWETH 계약에 첫 입금이 이루어진 후, 초기 잔액은 사용자가 송신자이자 수신자라는 점을 고려하여 기밀 이체에 사용되는 것과 동일한 공식에 따라 계산된 값으로 업데이트됩니다. 이러한 값과 키 쌍 생성 프로세스와 관련된 기술적 세부 사항은 본 제안서의 후속 섹션에서 제공됩니다.

래핑 해제 작업은 개념적으로 매우 유사하므로 이 섹션에서는 다루지 않습니다.

2.2. 잔액 관리

ElGamal을 사용하여 숨겨진 잔액을 계산하기 위해 이산 대수를 계산하는 것을 피하기 위해 잔액의 두 가지 병렬 표현이 유지됩니다.

• ZK 증명을 통한 잔액 지식 검증에만 필요한 ElGamal 커밋입니다.
• DH 공유 키로 암호화된 잔액은 사용자가 실제 잔액 데이터를 디크립트(Decrypt) 수 있도록 합니다. 복호화를 수행하려면 발신자의 공개 키 배열과 암호화 nonce 배열에 대한 접근 권한이 필요합니다.

ZK 증명은 사용자의 현재 잔액에서 생성되므로, 거래 실행 전에 잔액을 변경하면 증명이 무효화될 수 있습니다. 이 문제를 해결하려면 두 가지 유형의 잔액(ElGamal 커밋 및 DH 암호화)을 두 가지 별도의 상태로 제공해야 합니다.

• 토큰을 받기 위해 대기 중인 잔액입니다.
• 토큰을 사용할 실제 잔액입니다.

사용자는 언제든지 보류 중인 잔액에서 실제 잔액으로 토큰을 이동할 수 있습니다. 또한, 사용자가 시작한 각 이체가 끝날 때마다 이동할 수도 있습니다. 이 방식을 사용하면 잔액 업데이트를 단일 작업으로 통합하여 두 개의 별도 거래에 비해 가스 사용량을 줄일 수 있습니다.

2.3. 기밀 전송

기밀 이체를 시작하려면 네 가지 형태로 표현된 토큰 금액을 제공해야 합니다.

• 수신자의 공개 키 기반 ElGamal 커밋 내부에 숨겨져 있습니다.
• 발신자의 공개 키 기반 ElGamal 커밋 내부에 숨겨져 있습니다.
• 수신자의 잔액을 증가시키기 위해 수신자의 공개 키 기반 DH 공유 키로 암호화됩니다.
• 새로운 발신자의 잔액에 대한 발신자의 공개 키 기반 DH 공유 키로 암호화됩니다.

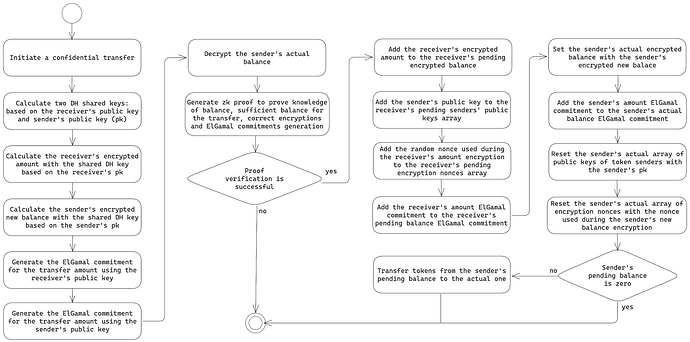
아래 다이어그램은 기밀 전송 프로세스를 보여줍니다.

그림 2: 기밀 전송 흐름 1999×993 292KB

이체 과정에서 두 가지 유형의 잔액과 관련 금액이 모두 업데이트되어 서로 다른 잔액 표현 간의 일관성이 보장됩니다.

DH 공유 키와 ElGamal 커밋 표현으로 암호화된 두 가지 동일한 값의 두 가지 버전이 존재한다는 점에 유의하십시오. 하나는 송신자의 공개 키 기반이고 다른 하나는 수신자의 공개 키 기반입니다. 이는 암호화 및 커밋 생성 과정에서 사용되는 서로 다른 접근 방식 때문에 발생하며, 이에 대한 기술적 세부 사항은 제안서의 후속 섹션에서 설명합니다.

3. 기밀 유지 수학

3.1. 기밀 키 쌍을 위한 KDF

이 프로토콜은 결정론적 KDF 방식을 사용하여 기밀 키 쌍을 생성합니다. 사용자는 이더리움(ECDSA) 개인 키로 이더리움 개선 제안(EIP)-712 구조화된 메시지에 서명해야 합니다. 서명의 해시 babyJubJub 개인 키입니다.

이더리움 개선 제안(EIP)-712 메시지는 다음과 같이 얻어집니다.

 bytes32 KDF_MSG_TYPEHASH = keccak256(“KDF(address cWETHAddress)”); bytes32 kdfStructHash = keccak256(abi.encode(KDF_MSG_TYPEHASH, cWETHAddress));

babyJubJub 개인 키는 다음과 같은 방법으로 얻습니다.

 signature = eth_signTypedData_v4(kdfStructHash) ; privateKey = keccak256(keccak256(signature)) ;

개인 키는 서명에서 직접 파생되므로 서명을 절대로 공개하지 않는 것이 중요합니다.

키 쌍은 다음을 만족해야 합니다.

1168×292 10.2KB

3.2. EC ElGamal 기반 약속 제도

EC ElGamal 체계에 기반한 공약은 ZK 증명에 적합한 간결한 표현을 가능하게 합니다. 또한 가산적 준동형 성질을 통해 원활한 잔액 관리를 용이하게 합니다.

잔액의 공약은 두 부분으로 구성되며 다음 공식에 따라 구성됩니다.

1170×412 14.2KB

ZK 증명을 통해 잔액의 약정을 효율적으로 증명하려면 사용자는 개인 키를 사용하여 집계된 난수 논스 에 대한 지식 부족을 보완해야 합니다.

918×122 2.88KB

송금액 약정은 송금인과 수취인에 따라 다르게 계산됩니다. 수취인의 약정액은 다음과 같이 계산됩니다.

1128×322 7.48KB

발신자 잔액 약정을 집계하는 데 사용되는 이체 금액 약정은 다음과 같이 계산됩니다.

1110×314 7.51KB

잔액 약정은 아래와 같이 추가적으로 계산됩니다.

1206×598 23.7KB

3.3. EC DH 공유 키를 사용한 암호화

ElGamal 커밋만으로는 사용자가 복호화된 잔액에 접근할 수 있는 편리한 수단을 제공하지 않고 이산 대수 문제를 풀어야 하므로, EC DH 공유 키를 사용하여 암호화를 통해 금액을 숨기는 추가적인 형태가 채택됩니다.

DH 공유 키는 다음과 같이 파생됩니다.

1130×286 16.5KB

전송량 DH 기반 암호화는 송신자와 수신자에 대해 다르게 수행됩니다.

수신자 잔액을 집계하는 데 사용되는 이체 금액의 암호화는 다음 공식에 따라 계산됩니다.

1192×466 23.4KB

무작위 논스) 사용은 암호화 체계의 무작위성 부족으로 인해 발생할 수 있는 잠재적인 전송 데이터 유출 문제를 해결하기 위해 필요하며, 이는 특히 반복 결제에서 두드러질 수 있습니다. 이러한 논스 값은 사용자가 잔액을 디크립트(Decrypt) 할 수 있도록 발신자의 공개 키와 함께 저장되어야 합니다.

암호화된 금액은 암호화된 수신자의 잔액을 집계하는 데 추가로 사용됩니다.

1224×538 18.6KB

공식에 따르면 수신자는 다음과 같이 잔액을 디크립트(Decrypt) 할 수 있습니다.

832×280 9.72KB

발신자 측에서 이 방식을 사용하여 이체 금액을 암호화하면 잔액 복호화에 필요한 공개 키와 난수 논스를 무한히 많이 관리해야 할 가능성이 있습니다. 이를 해결하기 위해 사용자가 토큰을 전송할 때마다 기존 발신자의 공개 키와 난수 논스 목록이 재설정됩니다. 이는 아래와 같이 암호화된 새 발신자의 잔액을 계산하여 수행됩니다.

1202×470 23.7KB

암호화된 잔액을 업데이트한 후, 보낸 사람은 자신의 공개 키와 무작위 논스 만을 단일 항목으로 관리하여 소유한 토큰의 총량을 디크립트(Decrypt) 해야 합니다.

새로운 잔액 계산에 대한 동일한 논리를 cWETH 토큰을 풀어서 사용할 수 있습니다.

4. 솔리디티 스마트 계약

4.1. 상태 변수

4.1.1. 공개 키

먼저, 각 사용자는 cWETH 계약에 첫 입금 시 생성된 해당 공개 키와 연결됩니다. 이는 간단한 mapping(address => uint256[2]) 을 통해 관리됩니다.

4.1.2. 균형

각 사용자의 잔액은 ElGamal 약정 양식에 표시됩니다.

 struct Commitment {uint256 [2] C;uint256 [2] D;}

DH 공유 키로 암호화된 잔액을 디크립트(Decrypt) 하려면 DH 잔액 자체와 함께 발신자의 공개 키 배열과 암호화 nonce 배열을 저장해야 합니다.

 struct DHBalance {uint256 encryptedBalance;uint256 [] [2] sendersPublicKeys;uint256 [] encryptionNonces;}

두 가지 잔액 유형 모두 보류 잔액과 실제 잔액의 형태로 제공되어야 하므로 최종 잔액 저장은 다음과 같습니다.

 struct Balance {Commitment elGamalCommitmentPending;Commitment elGamalCommitmentActual;DHBalance dhEncryptedPending;DHBalance dhEncryptedActual;}mapping(uint256 => Balance) internal balances;

내부 잔액 회계는 잔액 매핑의 키로 사용자 공개 키의 x 좌표를 사용하여 수행됩니다.

4.2. 함수

4.2.1. cWETH에 입금하기

올바른 기밀 계좌 생성을 위해서는 deposit 기능이 제공되어야 합니다.

 function deposit(uint256[ 2 ] publicKey, bytes calldata amountCommitmentData, bytes calldata balanceEncryptionData, bytes calldata proofData) external payable;

일반적인 ZK 증명과 함께 proofData 사용자가 제공된 공개 키에 대한 개인 키를 실제로 소유하고 있는지 확인하는 데 필요합니다.

amountCommitmentData 는 다음과 같이 추가로 디코딩됩니다.

 (uint256[2] commitmentC, uint256[2] commitmentD) = abi.decode(amountCommitmentData, (uint256[2], uint256[2]));

balanceEncryptionData 는 다음과 같이 디코딩됩니다.

 (uint256 encryptedBalance, uint256 encryptionNonce) = abi.decode(balanceEncryptionData, (uint256, uint256));

4.2.2. 기밀 전송

커밋 및 암호화 방식을 명확하게 이해하면 transfer 함수를 다음과 같이 지정할 수 있습니다.

 function transfer(address receiver, bytes calldata amountCommitmentData, bytes calldata amountEncryptionData, bytes calldata proofData) external;

amountCommitmentData 는 다음과 같이 추가로 디코딩됩니다.

 (uint256[2] senderCommitmentC, uint256[2] senderCommitmentD, uint256[2] receiverCommitmentC, uint256[2] receiverCommitmentD) = abi.decode(amountCommitmentData, (uint256[2], uint256[2], uint256[2], uint256[2]));

amountEncryptionData 는 다음과 같이 디코딩됩니다.

 (uint256 newEncryptedBalance, uint256 senderEncryptionNonce, uint256 receiverEncryptedAmount, uint256 receiverEncryptionNonce) = abi.decode(amountEncryptionData, (uint256, uint256, uint256, uint256));

4.2.3. cWETH 철회

cWETH 토큰을 풀기 위해서는 withdraw 기능이 제공되어야 합니다.

 function withdraw(uint256 amount, bytes calldata amountCommitmentData, bytes calldata balanceEncryptionData, bytes calldata proofData) external;

amountCommitmentData 는 다음과 같이 추가로 디코딩됩니다.

 (uint256[2] commitmentC, uint256[2] commitmentD) = abi.decode(amountCommitmentData, (uint256[2], uint256[2]));

balanceEncryptionData 는 다음과 같이 디코딩됩니다.

 (uint256 newEncryptedBalance, uint256 encryptionNonce) = abi.decode(balanceEncryptionData, (uint256, uint256));

5. 서콤 회로

이 제안서에 설명된 각 매개변수는 체인상에서 검증 가능하고 제로 지식 회로와 호환되도록 설계되었습니다.

5.1. cWETH 회로에 입금

cWETH 증명에 대한 입금을 위한 회로 신호 목록은 다음과 같습니다.

공공 신호:

• 사용자 공개 키;
• 보증금액;
• ElGamal은 사용자의 잔액에 대한 약속을 합니다.
• 엘가말의 보증금 금액 약속;
• 입금 후 사용자 잔액은 사용자의 공개 키 기반 DH 키로 암호화됩니다.
• 암호화 난수 논스.

개인 신호:

• 사용자 개인 키;
• ElGamal 커밋에 사용된 무작위 논스 .

이러한 신호를 작동시키려면 회로에 다음과 같은 제약 조건이 있어야 합니다.

1. 제공된 개인 키는 실제로 제공된 공개 키의 개인 키입니다.
2. 제공된 예치금액은 ElGamal 기반 약정을 사용하여 약정된 금액임이 입증됩니다.
3. 입금 후 사용자의 잔액은 DH 공유 키로 암호화된 것으로 증명됩니다.

5.2. 기밀 전송 회로

기밀 전송 증명을 위한 회로 신호 목록은 다음과 같습니다.

공공 신호:

• 보낸 사람의 공개 키
• 수신자의 공개 키;
• 엘가말은 발신자 잔액에 대한 약속을 합니다.
• ElGamal은 발신자의 공개 키를 기반으로 이체 금액을 약속합니다.
• ElGamal은 수신자의 공개 키를 기반으로 이체 금액을 약속합니다.
• 새로운 발신자의 잔액은 발신자의 공개 키 기반 DH 공유 키로 암호화됩니다.
• 발신자의 새로운 잔액 암호화에 사용되는 무작위 논스 .
• 수신자의 공개 키 기반 DH 공유 키로 암호화된 전송 금액;
• 수신자의 전송량 암호화 중에 사용되는 무작위 논스 .

개인 신호:

• 보낸 사람의 개인 키
• 보낸 사람의 잔액
• 이체 금액;
• 발신자의 ElGamal 커밋에 사용되는 무작위 논스 .
• 수신기의 ElGamal 커밋에 사용되는 무작위 논스 .

이러한 신호를 작동시키려면 회로에 다음과 같은 제약 조건이 있어야 합니다.

1. 제공된 개인 키는 실제로 제공된 발신자의 공개 키의 개인 키입니다.
2. 제공된 발신자 잔액은 ElGamal 약정을 사용하여 약정된 잔액이며 이체 금액보다 크거나 같은 것으로 입증됩니다.
3. 송금인의 ElGamal 송금 약정이 올바르게 생성되었습니다.
4. 수신자의 ElGamal 이체 금액 약정이 올바르게 생성되었습니다.
5. 새로운 발신자의 잔액은 발신자의 공개 키 기반 DH 공유 키로 올바르게 암호화되었습니다.
6. 이체 금액은 수신자의 공개 키 기반 DH 공유 키로 올바르게 암호화되었습니다.

5.3. cWETH 회로에서 철수

cWETH 증명을 철회하기 위한 회로 신호 목록은 다음과 같습니다.

공공 신호:

• 사용자 공개 키;
• 수신자 주소;
• 출금 금액;
• ElGamal은 사용자의 잔액에 대한 약속을 합니다.
• ElGamal은 사용자의 공개 키를 기반으로 인출 금액을 약속합니다.
• 출금 후 잔액은 사용자의 공개 키 기반 DH 공유 키로 암호화됩니다.
• 새로운 잔액 암호화 중에 사용되는 무작위 논스 .

개인 신호:

• 사용자 개인 키;
• 사용자 잔액;
• ElGamal 커밋에 사용된 무작위 논스

이러한 신호를 작동시키려면 회로에 다음과 같은 제약 조건이 있어야 합니다.

1. 제공된 개인 키는 실제로 제공된 공개 키의 개인 키입니다.
2. 제공된 발신자의 잔액은 ElGamal 약정을 사용하여 약정된 잔액이며 출금 금액보다 크거나 같은 것으로 입증됩니다.
3. ElGamal의 출금 금액 약정이 올바르게 생성되었습니다.
4. (출금 후) 새로운 잔액은 사용자의 공개 키 기반 DH 공유 키로 올바르게 암호화되었습니다.

참고문헌

솔라나(Solana) 재단. 기밀 토큰 연장. 2022.
베네딕트 뷜츠 외. 제더: 스마트 계약 환경에서의 프라이버시를 향하여. 2020.