요약
단순화된 범위 증명. 이더리움 가상 머신(EVM) 에서 페데르센 커밋 기반 프라이버시 코인의 범위 증명을 검증하는 데는 ECMUL 6개와 ECADD 3개(37K 가스)만 필요합니다. 첫 번째 설정 및 커밋에는 zkSNARK가 필요하지만, 그 이후부터는 비용이 최소화됩니다. 클라이언트 측에서 각 트랜잭션을 생성할 때에도 ZKP 계산이 필요하지 않습니다.
보안 증명이 포함된 전체 논문: https://eprint.iacr.org/2025/1811.pdf
단계:
G, H, B는 곡선 위의 독립적인 점입니다.
각 증명자(토큰 발신자)에 대한 일회성 설정
- a ← Zq를 샘플링하고 공개 앵커 U = aB로 설정합니다.
- 곡선 위에 점을 갖는 머클 트리를 만듭니다. 각 X ∈ {1, . . . , 2 n}에 대해 리프 페이로드 aXG를 정의합니다.
- 체인에 NIZK가 있는 경우 aXG로 구성된 트리의 머클 루트를 증명합니다. (범위 사전 증명)
증명(토큰을 보낼 때)
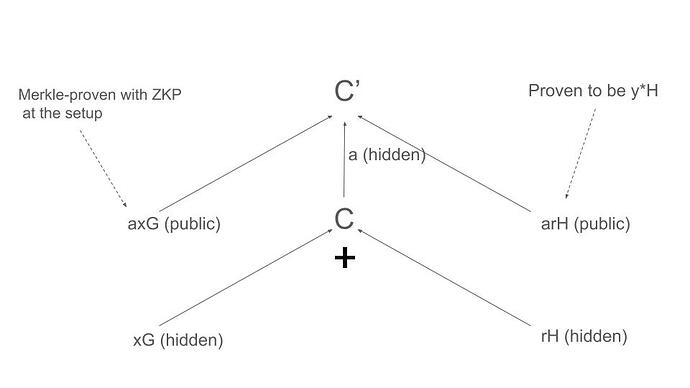
- 토큰 양 x와 r을 숨긴 채로 Pedersen Commitment C = xG + rH를 만듭니다. (x, r, xG, rH는 노출되어서는 안 됩니다)
- C, C' = aC, axG 및 해당 Merkle 증명, (U, B) 및 (C', C)에 대한 Chaum-Pedersen DLEQ 증명, arH 및 (arH, H)에 대한 Schnorr 프로토콜 증명을 제출합니다.
(C가 이더리움 가상 머신(EVM) 의 범위 내에 x와 함께 있는지) 확인
1, Chaum-Pedersen DLEQ를 사용하여 (U, B)와 (C', C)가 동일한 이산 행렬을 갖는지 확인합니다.
2. Schnorr 프로토콜이나 ECDSA를 사용하여 증명자가 H로부터 arH를 만들 수 있는지 확인합니다.
3. 설정 트리에서 axG의 Merkle Proof를 확인하세요.
4. C' = axG + arH를 확인하세요.
## Chaum-Pedersen DLEQ와 U=aB가 필요한 이유
Schnorr 프로토콜이나 ECDSA를 사용하여 (C', C)의 관계를 검사하는 경우 악의적인 증명자는 C' = yC 및 C = (bigX)G + rH(여기서 y = ax/(bigX))를 만들 수 있습니다. yrH도 검증됩니다.
나무를 더 작게 만드는 방법
모든 양의 숫자와 논스를 포함하는 트리를 만드는 것은 비트(Bit) 어려울 수 있습니다. 제한된 난수를 사용하여 점의 트리를 만들고, 리프 노드에 스칼라 숫자를 곱한 후 체인에 점을 추가하면 트리 곡선의 점들을 통해 난수를 추측할 수 없으므로 많은 도움이 될 것입니다.