0xAlpha는 DODO 연구에 기여했습니다. zk-SNARK 기술을 심층적으로 분석하고 암호화 및 블록체인의 개인정보 보호를 위한 원리와 응용 프로그램을 살펴보겠습니다.
작성자: 0xAlpha 공동 창립자 @DeriProtocol
편집자: DODO Research
트위터 팔로우를 환영합니다: @0x_Alpha

0xAlpha는 DODO 연구에 기여했습니다. 이 기사에서는 이 기술을 수학적으로 해석하여 정보를 공개하지 않고도 지식의 진실을 증명할 수 있는 방법을 밝힐 것입니다. 준비하세요. zk-SNARK의 미스터리를 밝혀보세요.
소개하다
zk-SNARK, "영지식 간결 비대화형 지식 인수"는 검증 자가 증인 정보 자체를 공개하지 않고 특정 관계를 만족시키는 증인 이라는 특정 지식을 보유하고 있는지 검증자가 확인할 수 있도록 합니다.
특정 문제에 대한 zk-SNARK 생성에는 다음 네 단계가 포함됩니다.
- 문제(또는 함수)를 산술 게이트 회로로 변환합니다.
- 그런 다음 이 회로는 행렬 공식으로 변환됩니다.
- 이 행렬 공식은 특정 최소 다항식으로 나누어져야 하는 다항식으로 추가로 변환됩니다.
- 마지막으로, 이 분할성은 증명이 진행되는 유한 필드의 타원 곡선 점으로 표현됩니다.
처음 세 단계는 단지 원래 문장의 표현을 변환하는 것뿐입니다. 마지막 단계에서는 동형암호를 사용하여 3단계의 진술을 암호화된 공간에 투영함으로써 증명자가 그 안에 있는 미러 진술을 확인할 수 있습니다. 이 예측이 비대칭 암호화를 사용한다는 점을 고려하면 3단계의 명령문에서 원래 명령문으로 역추적하여 영지식 노출을 보장하는 것은 불가능합니다.
이 기사를 읽는 데 필요한 수학적 배경은 STEM 전공의 첫 번째 수준 대수학에 해당합니다. 도전적일 수 있는 유일한 개념은 타원 곡선 암호화일 수 있습니다. 이에 익숙하지 않은 분들을 위해, 역함수는 아직 풀리지 않은 상태라는 점을 염두에 두고 특수한 밑수를 갖는 지수 함수로 생각하세요.

이 기사에서는 계속해서 방정식 (1)을 논의의 기초로 사용할 것입니다.
1단계: 산술 게이트 회로
방정식 (1)은 다음과 같은 기본 산술 연산으로 나눌 수 있습니다.
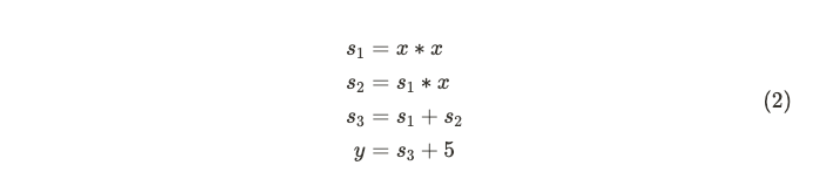
이는 다음 산술 게이트 회로에 해당합니다.
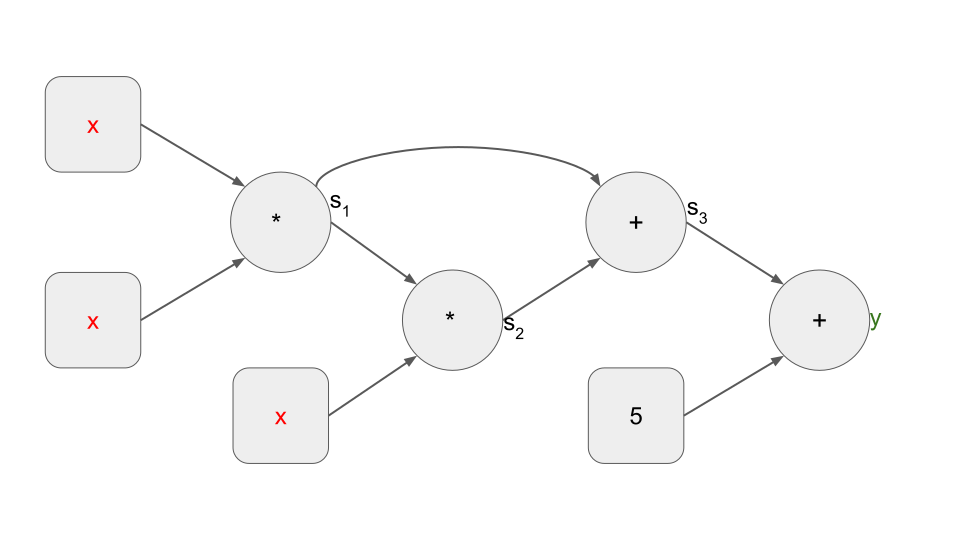
우리는 또한 식 (2)를 4개의 "첫 번째 수준 제약 조건" 세트로 참조하며, 각 제약 조건은 회로의 산술 게이트 관계를 설명합니다. 일반적으로 n개의 첫 번째 수준 제약 조건 집합은 다음에 설명되는 QAP(2차 산술 프로그램)로 요약될 수 있습니다.
2단계: 매트릭스
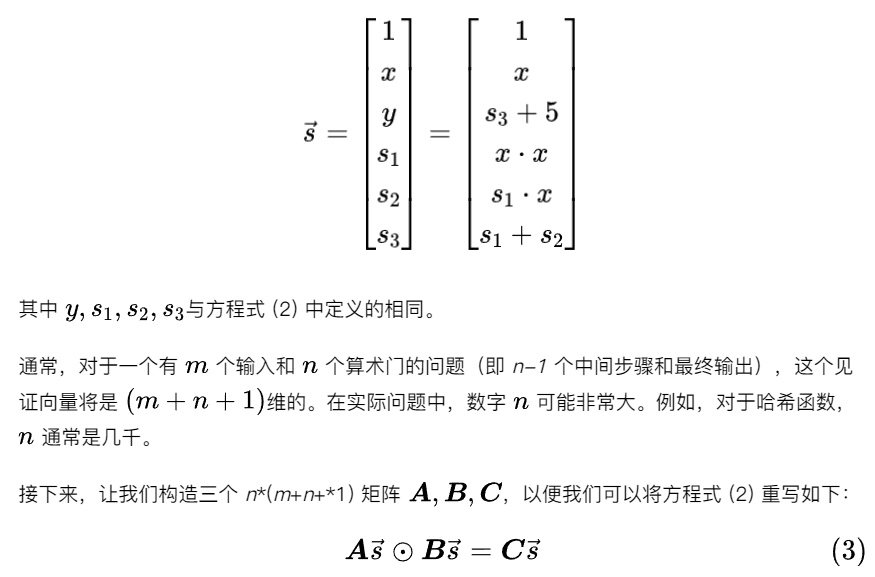
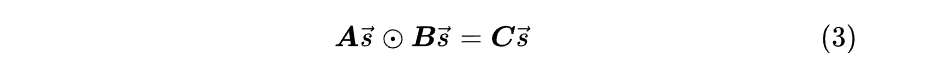
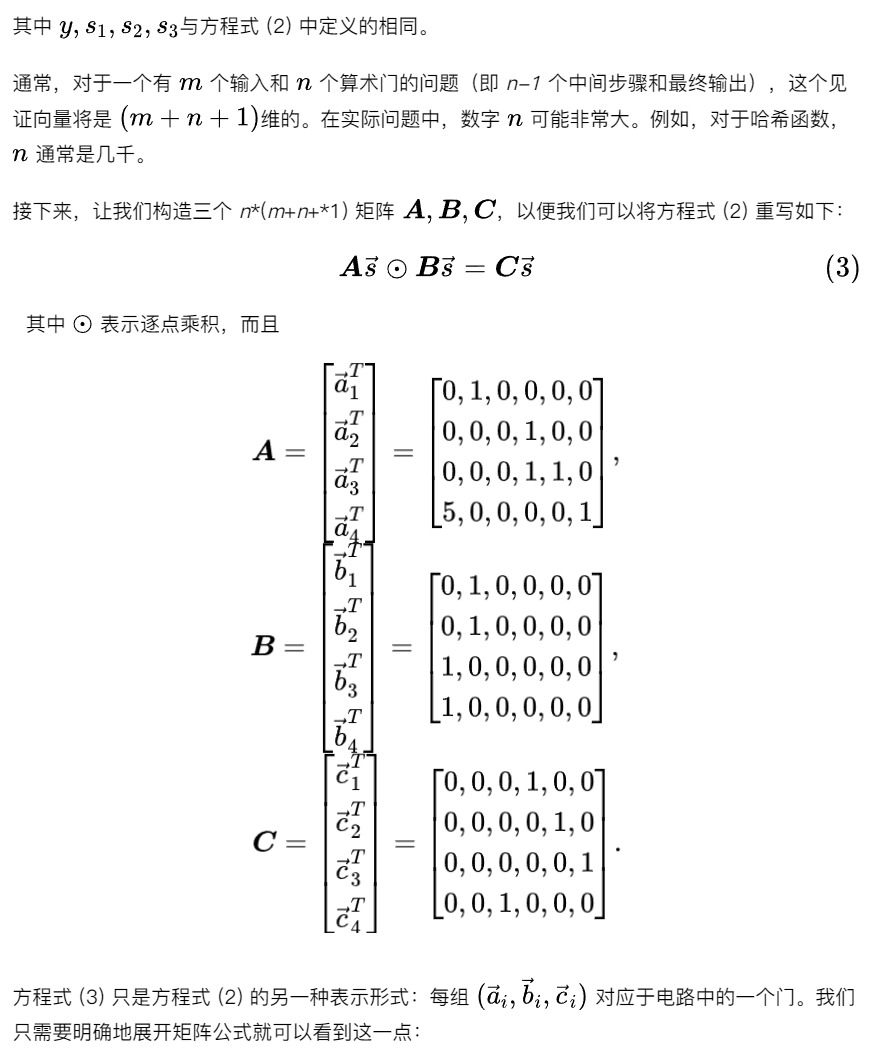
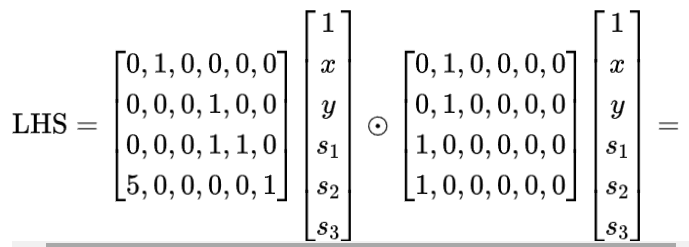
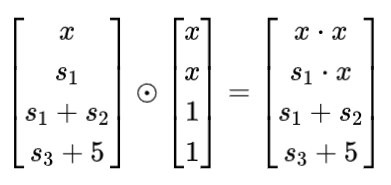

3단계: 다항식

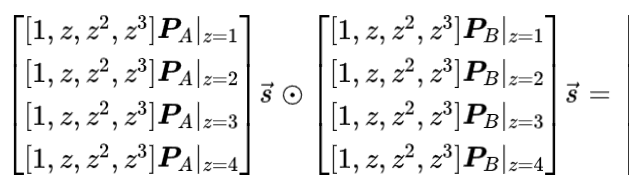
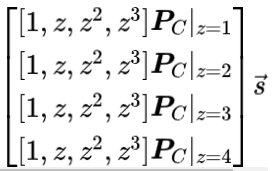
각 행을 추출하여 개별적으로 관찰하면 이 네 행이 네 지점에서 평가된 동일한 표현식에 해당한다는 것을 찾는 것이 어렵지 않습니다. 따라서 위의 행렬 방정식은 다음과 같습니다.

이를 증명하는 간단하지만 기밀이 아닌 방법은 방정식 (4)의 왼쪽을 제공하고 인수분해를 보여주는 것입니다. 그러나 zk-SNARK의 주요 목적은 은밀한 상태를 유지하는 것입니다(지식을 공개하지 않음). 따라서 우리는 이 방정식을 직접 증명하지 않고 타원 곡선 점 공간에서 암호화된 버전을 증명할 것입니다.
4단계: 타원 곡선 점
방정식 (4)를 다음과 같이 다시 작성하십시오.

다음으로 실제 단계를 더 자세히 설명하겠습니다.
타원곡선 암호화

반면에 두 개의 타원 곡선 점을 추가하는 것은 아래와 같이 정의됩니다.


그러나 앨리스가 증명하려는 방정식 (5)는 2차 형태이므로 충분히 선형적이지 않습니다. 2차 항을 처리하려면 암호화된 공간에서 곱셈을 정의해야 합니다. 이를 페어링 함수 또는 쌍선형 맵 이라고 하며 다음에 설명됩니다.
이중선형 매핑

이것은 우리 모두에게 익숙한 덧셈과 곱셈 연산의 분배 법칙입니다.
이러한 이중선형 매핑을 사용하면 방정식 (5)의 양쪽을 암호화 공간에 매핑할 수 있습니다.
공개 참조 문자열

전체 프로세스를 "인증 키", 줄여서 VK라고 합니다. 여기에는 검증자에게 제공해야 하는 타원 곡선 점(ECP) 7개가 포함됩니다. 문제에 얼마나 많은 입력과 1차 제약 조건이 관련되어 있더라도 VK는 항상 7개의 ECP로 구성된다는 점에 유의해야 합니다.
또한 특정 문제에 대해 "신뢰할 수 있는 설정"과 PK 및 VK 생성 프로세스는 한 번만 수행하면 된다는 점을 언급할 가치가 있습니다.
증명 및 검증
이제 공개 키(PK)를 소유한 Alice는 다음 ECP(타원 곡선 점)를 계산합니다.
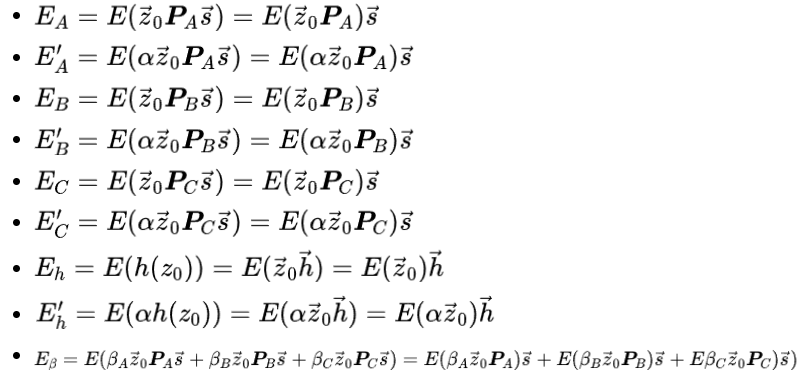
이 9개의 타원 곡선 점은 영지식 간결 비대화형 증명(zk-SNARK)의 핵심입니다!
Alice는 실제로 공개 키의 타원 곡선 점에 대해 일부 선형 조합 작업을 수행했습니다. 이는 특히 중요하며 확인 중에 확인됩니다.
이제 Alice는 zk-SNARK 인증서를 넘겨주었고, 마침내 3단계로 나누어진 검증 과정에 들어갑니다.

참고자료
- “Zk-SNARKs: Under the Hood” (비탈릭 부테린)
- “영지식 증명 검토”(Thomas Chen, Abby Lu, Jern Kunpittaya 및 Alan Luo)
- "zk-SNARK가 작동하는 이유와 방법: 명확한 설명"(Maksym Petkus)
- 웹사이트: 영지식 증명
- 위키피디아: 타원 곡선
- Wikipedia: 유한장
- Wikipedia: 페어링 기반 암호화
부인 성명
본 연구보고서에 실린 정보는 공개된 자료를 바탕으로 작성되었으며, 본 글에 표현된 의견은 연구 목적으로만 제시된 것이며 어떠한 투자 의견도 대변하지 않습니다. 보고서에 제시된 의견과 예측은 발행일 당시의 분석과 판단일 뿐이며 영구적인 타당성을 갖지 않습니다.
면책조항: 블록체인 정보 플랫폼으로서 이 사이트에 게시된 기사는 작성자와 게스트의 개인적인 의견만을 나타낼 뿐이며 Web3Caff의 입장과는 아무런 관련이 없습니다. 이 글의 내용은 정보 공유만을 위한 것이며 투자 조언이나 제안을 구성하지 않습니다.귀하가 위치한 국가 또는 지역의 관련 법률 및 규정을 준수하시기 바랍니다.