Kucoin: Mô hình quản lý giới hạn rủi ro mới

Tác giả: Michael Gan, Nhà sáng lập KuCoin; Ken Tian, Trưởng phòng phái sinh

Tổ chức: KuCoin

1 Lời mở đầu

Nhiều sàn giao dịch tiền điện tử đã áp dụng các biện pháp quản lý rủi ro phức tạp để ngăn ngừa rủi ro thanh lý. Những biện pháp này bao gồm thiết lập các giới hạn rủi ro nhiều cấp độ và hạn chế việc sử dụng đòn bẩy cao. Ngoài ra, các sàn giao dịch cũng điều chỉnh động các thông số như giới hạn rủi ro và tỷ lệ ký quỹ dựa trên giá của tài sản cơ sở và thanh khoản thị trường. Tuy nhiên, những quy trình này không chỉ phức tạp mà còn thiếu các tiêu chuẩn quản lý rõ ràng, đòi hỏi phải đầu tư nhiều nguồn lực để duy trì một hệ thống có thể tồn tại sự không nhất quán nội bộ - ví dụ, tăng vốn không nhất thiết mang lại vị thế lớn hơn vì mức đòn bẩy có thể thay đổi đột ngột.

Trên một số nền tảng giao dịch (xem Hình 1), có hàng trăm cấp độ giới hạn rủi ro. Những thay đổi cấp độ thụ động này làm tăng độ phức tạp trong quản lý hệ thống và có thể dẫn đến một số thanh lý cưỡng bức, gây thiệt hại cho lợi ích của người dùng.

Mục tiêu của chúng tôi là phát triển một mô hình phi tuyến tính để mô phỏng kích thước vị thế hợp lý dựa trên vốn cho phép quản lý rủi ro linh hoạt và hiệu quả hơn. Phương pháp này liên quan đến việc tái cấu trúc hệ thống công thức nội bộ để đạt được tính nhất quán, cung cấp một giải pháp thay thế khả thi cho mẫu giới hạn rủi ro phức tạp hiện tại.

Bài báo này đề xuất một khuôn khổ quản lý rủi ro mới để thay thế các mô hình giới hạn hiện tại. Phương pháp này đã được triển khai trong hệ thống ký quỹ chéo của KuCoin, thể hiện một số ưu điểm rõ ràng:

1. Gần với cài đặt quản lý vị thế của các sàn giao dịch truyền thống, giúp vốn của các tổ chức dễ dàng thích ứng hơn.

2. Không cần điều chỉnh giới hạn rủi ro dựa trên kích thước vị thế hoặc mức sử dụng đòn bẩy.

3. Đơn giản hóa quy trình vận hành, giảm gánh nặng cho sàn giao dịch và giảm nguy cơ ảnh hưởng đến lợi ích của người dùng để bảo vệ lợi ích của chính sàn giao dịch.

Mô hình này cung cấp một cách tiếp cận minh bạch và đơn giản hơn cho quản lý rủi ro, làm cho hoạt động của sàn giao dịch và lợi ích của người dùng được cân bằng hơn.

2 Mô hình

2.1 Kích thước vị thế tối đa

Giả sử người dùng có số dư tài khoản là C, giá hợp đồng tương lai của tài sản cơ sở là p. Tỷ lệ ký quỹ ban đầu r tương ứng với nghịch đảo của đòn bẩy mà người dùng lựa chọn. Bỏ qua phí giao dịch, số hợp đồng mà người dùng có thể mở là:

Tuy nhiên, khi C quá lớn hoặc r quá thấp, rủi ro đối với sàn giao dịch sẽ tăng đáng kể. Do đó, khi C và r cố định và C lớn, hệ thống phân cấp rủi ro của sàn giao dịch sẽ hạn chế kích thước vị thế tối đa, thường thấp hơn nhiều so với C/(p*r). Ngược lại, đối với C nhỏ, kích thước vị thế sẽ gần với C/(p*r) hơn.

Nhiều sàn giao dịch sử dụng từ hàng chục đến hàng trăm cấp độ rủi ro để quản lý mối quan hệ này. Do đó, khi vốn của người dùng tăng lên, họ thường phải điều chỉnh cấp độ rủi ro của mình. Mục đích của những hạn chế này có thể được biểu thị gần đúng bằng hàm logarit như sau:

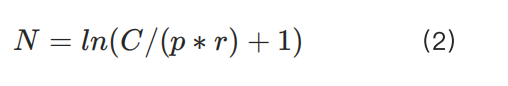
Rõ ràng, khi C lớn, đạo hàm bậc nhất của hàm logarit giảm, có nghĩa là kích thước vị thế có thể đạt được sẽ nhỏ hơn kết quả tính theo công thức tuyến tính. Tuy nhiên, điều này đặt ra một thách thức: để xấp xỉ ln(x+1)≈x, C phải đủ nhỏ và p phải đủ lớn. Nếu không, ngay cả khi C nhỏ, người dùng vẫn có thể không thể đạt được kích thước vị thế tối đa lý thuyết C/(p*r).

Để giải quyết vấn đề này, chúng tôi cần giới thiệu một tham số mở rộng k lớn hơn dựa trên đặc điểm của từng loại hợp đồng, sửa đổi công thức ban đầu như sau:

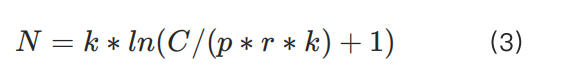
Điều chỉnh này đáp ứng nhu cầu của người dùng có vốn nhỏ, đồng thời cũng phù hợp với yêu cầu kiểm soát rủi ro của người dùng có vốn lớn.

Trong hệ thống ký quỹ chéo của KuCoin, xét đến các vị thế đã mở và các yêu cầu ký quỹ khác, chúng tôi định nghĩa các biến sau:

•F: Ký quỹ được sử dụng bởi các hợp đồng và lệnh chưa thực hiện khác.

•E: Tổng quyền lợi trong tài khoản tương lai của người dùng.

•Q: Kích thước vị thế của các lệnh chờ phù hợp với hướng của lệnh mới.

•O: Kích thước vị thế hiện tại (nếu phù hợp với hướng của lệnh mới thì là giá trị dương, ngược lại là giá trị âm).

Công thức tính kích thước vị thế tối đa như sau:

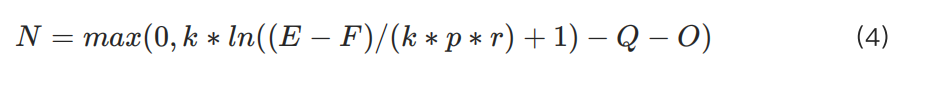
Do đó, trong mô hình của KuCoin,ối với quy mô vốn điển hình, mối quan hệ giữa đòn bẩy và kích thước vị thế tối đa có thể được biểu diễn như biểu đồ sau:

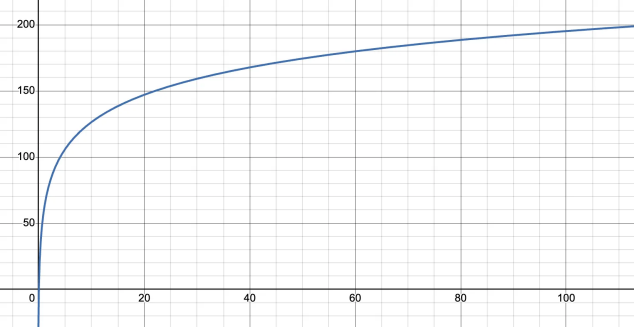
Biểu đồ này cho thấy cách mô hình cân bằng giữa quy mô và ổn định thông qua điều chỉnh ký quỹ phi tuyến, đáp ứng nhu cầu tối đa hóa vị thế của người dùng có vốn nhỏ, đồng thời bảo đảm kiểm soát rủi ro cho người dùng có vốn lớn.

Tuy nhiên, trên hầu hết các sàn giao dịch (như OKX và Binance), mối quan hệ giữa đòn bẩy và kích thước vị thế thường thể hiện một đường cong méo mó:

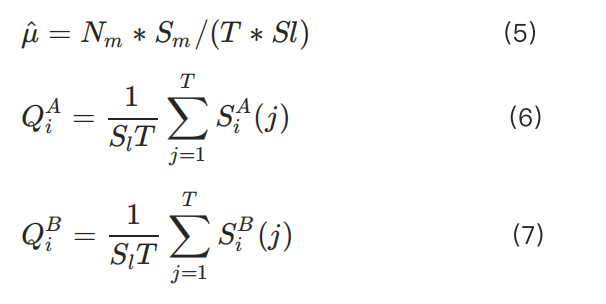
Thực tế, thậm chí tỷ lệ ký quỹ duy trì (MMR) cũng thể hiện một mô hình tương tự. Điều này đặc biệt thách thức đối với người dùng có vốn lớn. Ví dụ, khi tỷ lệ ký quỹ ban đầu (IMR) được đặt ở mức 50%, MMR có thể lên tới 48%. Trong trường hợp này, người dùng cố gắng mở vị thế lớn bị hạn chế chỉ có thể sử dụng đòn bẩy thấp, nhưng MMR lại tăng lên mức không hợp lý.

Cách thiết lập này hạn chế khả năng người dùng sử dụng hiệu quả vốn của mình, vì các mức đòn bẩy thay đổi đột ngột yêu cầu điều chỉnh thường xuyên, làm giảm tính linh hoạt. Điều này tạo ra sự mất cân bằng giữa quản lý rủi ro và trải nghiệm người dùng, khiến các nhà đầu tư lớn khó hoạt động hiệu quả trong những hạn chế này.

2.2 MMR và IMR

MMR (tỷ lệ ký quỹ duy trì) chủ yếu được sử dụng để giúp sàn giao dịch quản lý rủi ro thanh lý, như một cơ chế bù đắp. Về bản chất, MMR phản ánh áp lực rút thanh khoản và cần được điều chỉnh động theo sự thay đổi của các vị thế chưa thanh toán. Sau đây là công thức lý thuyết của MMR dựa trên các chỉ số liên quan đến thanh khoản mà sàn giao dịch có thể tiếp cận.

2.2.1 Các biến liên quan đến thanh khoản

Để đánh giá chính xác thanh khoản, các biến sau đây được xác định, thường có thể nhìn thấy bởi sàn giao dịch:

•μ: Tốc độ thực hiện lệnh thị trường

•T: Thời gian thanh lý hoặc của sàn giao dịch

•i: Khoảng cách so với giá mua/bán tốt nhất (mức giá)

•j: Đơn vị thời gian của báo giá

•Qi: Số lượng trung bình của các lệnh cách xa vị trí i

•S: Kích thước trung bình của lệnh (sử dụng cho lệnh thị trường và lệnh giới hạn)

•N: Số lượng lệnh (sử dụng cho lệnh thị trường, hủy lệnh và lệnh giới hạn)

Những giá trị này đại diện cho tình huống trung bình trong thị trường ổn định.

2.2.2 Định nghĩa các chỉ số vị thế của người dùng

• position: Kích thước vị thế trung bình tức thời của tất cả người dùng, có thể thu thập từ dữ liệu lịch sử của sàn giao dịch.

• pos: Kích thước vị thế do một người dùng duy nhất nắm giữ.

• X: Tổng khối lượng giao dịch trong khoảng thời gian MMR.

• MMRup: Giới hạn trên của MMR.

• rMMR: Giá trị cuối cùng của MMR.

• R: Khoảng cách thực

Từ phương trình trên, có thể thấy rằng ngoài R, các biến khác như vị thế, Q, S và T đều đã được xác định. Do đó, có thể suy ra các biến này và tính toán MMR và rMMR. Ngoài ra, cần thiết lập giới hạn trên cho MMRup, vì mô hình thường có xu hướng ước tính bảo thủ, bỏ qua ảnh hưởng tích cực của các mức giá quan trọng và các lớp đặt lệnh mua bán đối với sổ lệnh. Một số nghiên cứu từ CME (xem Hình 2) thể hiện ảnh hưởng này chính xác hơn. IMR (tỷ lệ ký quỹ ban đầu) thường liên quan đến đòn bẩy và tính thanh khoản của tài sản cơ sở, vì vậy thường cần được điều chỉnh động theo các yếu tố như kích thước vị thế. Nó có thể được định nghĩa là:

Ở đây, IMR tương ứng với tỷ lệ ký quỹ ban đầu r được đề cập trong Mục 2.1. Hàm w(rMMR) cung cấp độ linh hoạt lớn hơn. Ví dụ, nếu sàn giao dịch cho rằng tính thanh khoản của nó tương đối ổn định, có thể sử dụng cách điều chỉnh đơn giản như: w(rMMR)=1.3×rMMR. Phương pháp này cung cấp một cách thực tế để điều chỉnh động tỷ lệ ký quỹ, đảm bảo IMR phản ánh tình trạng thị trường và mức độ thanh khoản hiện tại. So với quy tắc ký quỹ cố định, điều này làm cho hệ thống linh hoạt hơn, mang lại lợi ích cho cả người dùng và sàn giao dịch thông qua quản lý rủi ro hiệu quả.

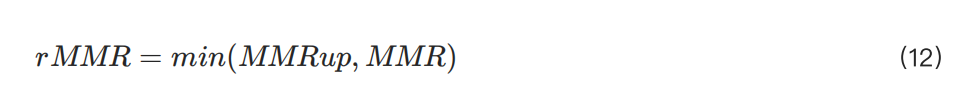
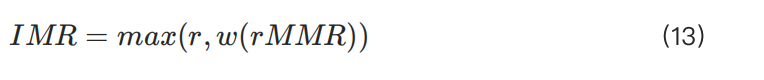
3 Giải gần đúng k

Tham số k là tham số toàn cầu được thiết lập cho từng tài sản (cặp giao dịch) cụ thể, không cần xem xét các lệnh hiện có hoặc vị thế chưa thanh toán. Nguyên tắc, giá trị k càng lớn, người dùng càng có thể mở nhiều vị thế hơn. Tuy nhiên, có một giới hạn quan trọng: số vị thế tối đa được phép không được vượt quá tổng vốn nhân với giá trị IMR. Để đơn giản hóa, chúng tôi sẽ gán công thức số vị thế tối đa cho biến :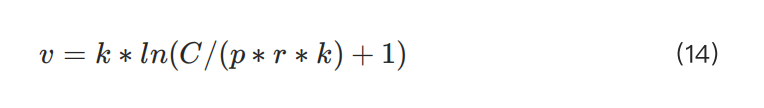

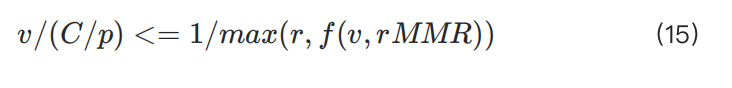
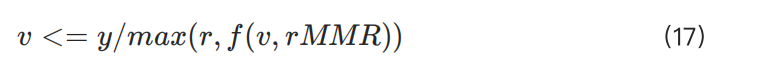
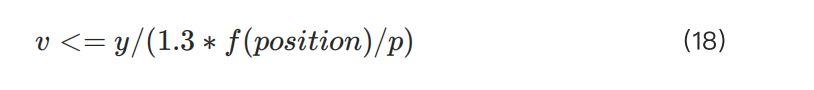
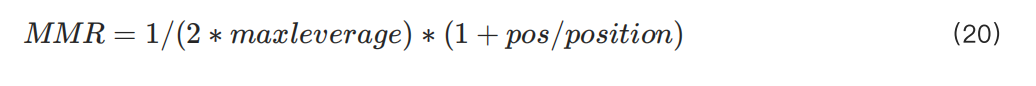
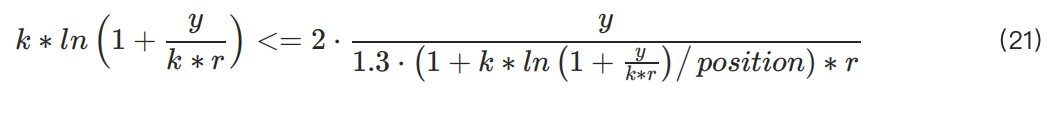
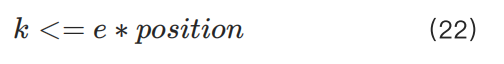
Đòn bẩy thực tế phải nhỏ hơn hoặc bằng nghịch đảo của ký quỹ đã sử dụng:

Chúng tôi giới thiệu biến mới y để thay thế C (vốn) và p (giá) để đơn giản hóa tính toán:

Kết quả là:

Ngoại trừ các vị thế rất nhỏ, việc điều chỉnh đơn giản 1.3 × rMMR (sử dụng f(pos,rMMR)) thường nhỏ hơn r. Đối với các vị thế nhỏ, ký quỹ cần thiết trở nên không đáng kể, vì vậy các tình huống như vậy không nằm trong mô hình rủi ro của chúng tôi. Tương tự, do MMRup đã đặt ra giới hạn trên, nó cũng có thể bỏ qua trong bối cảnh này. Do đó, chúng tôi chỉ cần xem xét giá trị nhỏ nhất có thể của 1/IMR. Bất đẳng thức này do đó có thể được đơn giản hóa thành:

Bất đẳng thức này thể hiện mối quan hệ giữa số vị thế tối đa được phép và đòn bẩy thực tế. Khác với các biến khác, vị thế và R có mối quan hệ nghịch đảo rõ ràng. Do đó, MMR được suy ra từ R cũng có thể tỷ lệ nghịch với vị thế và được biểu diễn như sau:

Giả sử ở điều kiện vị thế thấp, MMR tuân theo dạng truyền thống (một nửa nghịch đảo của đòn bẩy), công thức có thể được viết là:

Khi tìm giá trị giới hạn của k, công thức (3) sẽ thay r bằng 1/maxleverage. Sau khi thay thế biến, bất đẳng thức (18) có thể trở thành:

Chúng tôi nhận thấy rằng y (được xác định bởi vốn của người dùng) lý thuyết không nên ảnh hưởng đến giá trị của k. Do đó, k chủ yếu phụ thuộc vào vị thế. Mặc dù giá trị tối thiểu của k sẽ thay đổi theo y, mục tiêu là tìm ra giá trị tối thiểu có thể trong tất cả các điều kiện, đảm bảo an toàn khi mở vị thế trong bất kỳ kịch bản nào. Ở đây, y/(k*r) vẫn có thể được thay thế bằng một biến, nhưng phương trình vẫn phức tạp và khó giải bằng phương pháp giải tích. Sau nhiều thử nghiệm gần đúng và mô phỏng lặp lại, chúng tôi phát hiện ra rằng k sẽ hội tụ về một biểu thức rất đơn giản (nhưng tính toán k khá phức tạp, không được mô tả chi tiết ở đây):

Bằng cách điều chỉnh giá trị của k hoặc vị thế, người dùng có thể mở vị thế lên đến C/(p*r) khi lượng vốn hoặc số lượng vị thế chưa thanh toán không lớn. Nếu không, sẽ bị giới hạn. Quy mô và mức độ giới hạn được kiểm soát chung bởi k và vị thế. Do đó, các loại tiền điện tử khác nhau thường có các giá trị k khác nhau.

4 Kết luận

Trên đây là bản giới thiệu vắn tắt về hệ thống giới hạn rủi ro toàn phần của Kucoin. Ưu điểm và tính thân thiện với người dùng của thiết kế này là rõ ràng. Trong hệ thống toàn phần của Kucoin, ngoài giới hạn rủi ro, các yếu tố khác như tỷ lệ rủi ro và việc sử dụng ký quỹ lệnh cũng được quản lý động thông qua giá đánh dấu. Quản lý động này không chỉ giải phóng tối đa ký quỹ của người dùng, mà còn tích hợp một cách liền mạch với khung giới hạn rủi ro mới, nâng cao hiệu quả hệ thống và trải nghiệm người dùng.

5 Phụ lục

Hình 1: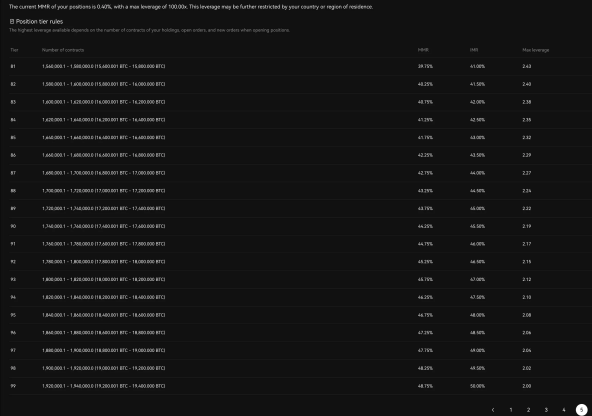

Hình 2:

6 Tài liệu tham khảo

1. Rama Cont, Sasha Stoikov và Rishi Talreja, "A Stochastic Model for Order Book Dynamics", Operations Research, 2010, Vol. 58, No. 3, pp. 549–563. 2. "Forecasting Initial Margin Requirements — A Model Evaluation", Journal of Financial Markets, Vol. 40, 2018. 3. Alfonsi, A., A. Schied, A. Schulz, "Optimal execution strategies in limit order books with general shape functions", Quant. Finance, 2010, Vol. 10, No. 2, pp. 143–157.