Khi tôi rời khỏi học viện, tôi đã tự hứa với lòng mình sẽ không viết thêm bài báo nào nữa. Nhưng thời buổi tuyệt vọng đòi hỏi những biện pháp tuyệt vọng! Một câu hỏi LVR làm tôi bận tâm trong nhiều năm. Sau đó @MartinTassy đã xuất hiện và giải quyết nó. Dưới đây là một Bit lịch sử và một số trực giác 1/số

Khi @jason_of_cs, @ciamac, @Tim_Roughgarden và @alz_zyd_ lần đầu tiên giới thiệu ý tưởng về LVR, họ đã thực hiện theo mô hình không có phí hoán đổi. Tất nhiên, điều này ngay lập tức đặt ra câu hỏi: LVR *ròng* sẽ là bao nhiêu trong mô hình có phí hoán đổi? 2/n moallemi.com/ciamac/papers/lvr...

Tôi đã nhờ hai người bạn (Dmitry Livdan, UC Berkeley và Alex Boulatov, Đại học HSE) chứng minh kết quả sau. Sự mất mát của LP là: * biến động theo khối * tỷ lệ nghịch với phí hoán đổi * tỷ lệ thuận với sqrt của Block Time Tuy nhiên vẫn còn hai vấn đề... 3/năm

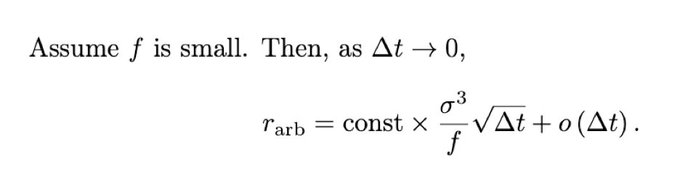
Đầu tiên, bằng chứng của chúng tôi có Bit mơ hồ (giống như phương trình Fokker–Planck) hoặc ít nhất là tôi hiểu như vậy. Thứ hai, tôi không thể tìm ra hằng số chính xác để phương trình có thể hoạt động được. Vì vậy, tất nhiên là tôi đã bỏ cuộc và thay vào đó là xóa một chủ đề trên Twitter 4/năm

Nhưng sau đó @jason_of_cs, @ciamac, @Tim_Roughgarden đã xuất bản bài viết "LVR with fees" của họ, trong đó có một số nội dung sau: * công thức chính xác cho việc mất LP trong mô hình có phí * bằng chứng đầy đủ về kết quả Họ đã có thể hoàn thành việc này... 5/n moallemi.com/ciamac/papers/lvr...

với một giả định tao nhã: các khối đến theo một tiến trình Poisson. Giả định này mang tính mô tả cho các chuỗi Bằng chứng công việc (PoW) . Nhưng hầu hết các chuỗi Bằng chứng cổ phần (PoS) đều có thời gian Block cố định. Điều này khiến tôi suy nghĩ: giữ nguyên Block Time trung bình, thì... 6/năm

tác động của sự không chắc chắn về Block Time đối với tổn thất NHÀ CUNG CẤP THANH KHOẢN đối với các nhà đầu cơ chênh lệch giá? Về cơ bản, chúng ta vẫn cần xác định hằng số đó! Tôi đã khóa cửa. Tôi ngừng đọc sách cho con tôi. Hủy tư cách thành viên phòng tập. Nói với bạn bè rằng tôi đang gặp vấn đề về sức khỏe. Hỏi mọi giáo sư thống kê mà tôi biết... 7/năm

Sau đó tôi nhớ ra rằng @MartinTassy và @_Dave__White_ đã từng làm việc với một câu hỏi tương tự trước đây nhưng sử dụng các công cụ hơi khác nhau. (Tôi làm nhiều nhất có thể trong thời gian liên tục và sau đó tìm ra điều gì xảy ra trong một mô hình rời rạc gần đó, nhưng họ đã đi theo hướng ngược lại) 8/n

Vì vậy, tôi đã liên lạc với Martin. Một điều khá rõ ràng khi so sánh các mô hình với thời gian cố định và Block Poisson đến. Sự mất mát của LP là tích của: Xác suất hoán đổi ARB * Tổn thất trên mỗi lần hoán đổi chênh ARB . Hóa ra là *xác suất* của một giao dịch hoán đổi ARB ... 9/năm

chỉ là một hàm của Block Time*trung bình*. Không quan trọng nếu các khối đến theo các khoảng thời gian không đổi hay theo mô hình Poisson. Nhưng tổn thất cho mỗi giao dịch hoán đổi chênh lệch giá sẽ nhỏ hơn khi thời gian Block được cố định. Tại sao? Mức lỗ tăng theo giá Sàn tập trung (CEX) ... 10/năm

vượt quá mức Chênh lêch giá mua bán của Sàn phi tập trung (DEX) trong thời gian liên khối. Để vượt quá, giá Sàn tập trung (CEX) trước tiên cần phải đạt đến ranh giới của mức chênh lệch, sau đó sử dụng thời gian còn lại cho đến Block tiếp theo để vượt quá. Trong mô hình Poisson, nếu Block Time trung bình là 12 giây... 11/năm

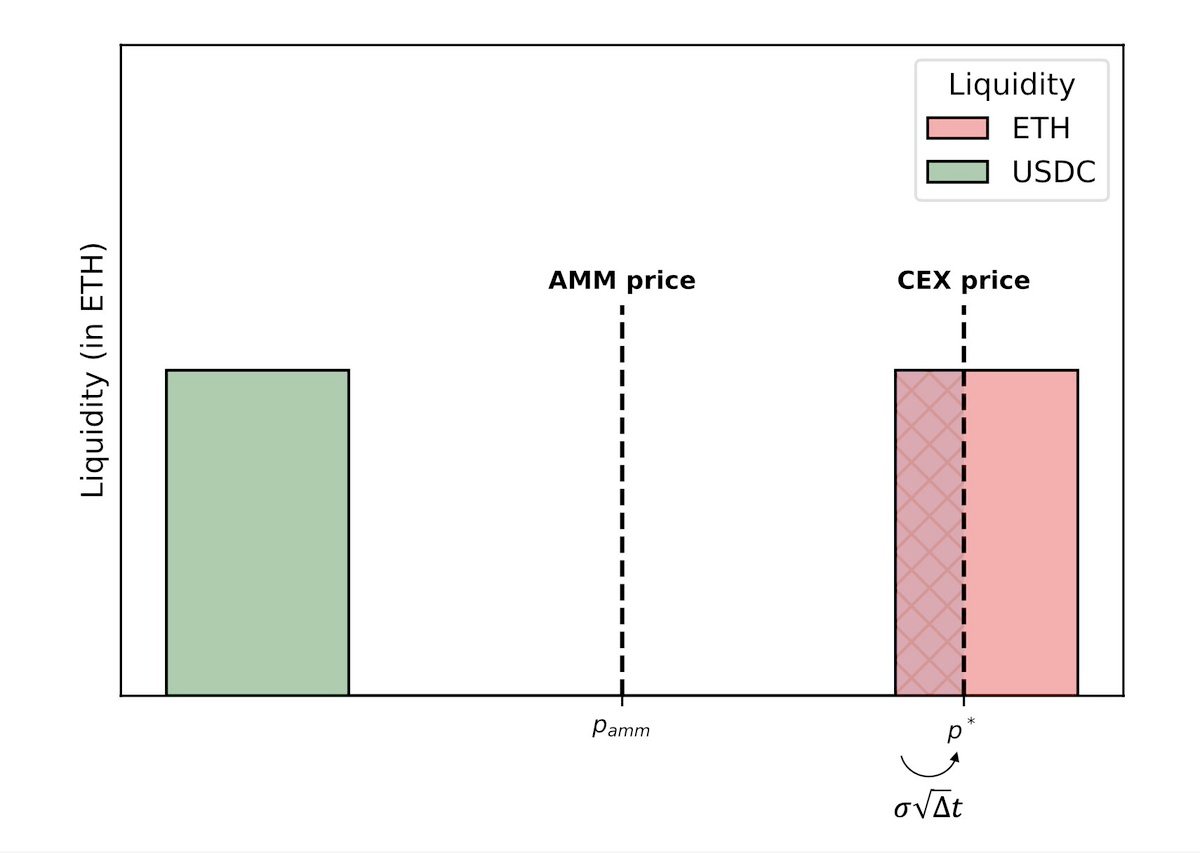
và giá đạt đến ranh giới 2 giây sau Block trước đó, thì trung bình vẫn có 12 giây cho sự vượt ngưỡng. Nhưng với thời gian Block cố định, nó sẽ chỉ có 10 giây. Trong bài báo dưới đây, Martin và tôi cung cấp biểu thức chính xác về mức mất mát với thời gian Block cố định. 12/năm

Hóa ra hằng số chúng ta đang tìm kiếm bao gồm hàm zeta Riemann được đánh giá ở mức 1/2. Tôi cảm thấy chúng ta đang tiến gần đến việc kết nối nghiên cứu Nhà tạo lậo trị trường tự động (AMM) với giả thuyết Riemann, điều này khá ấn tượng vì mọi thứ bắt đầu với xy=k! http:/arxiv.org/pdf/2505.05113