Tác giả gốc: Weikeng Chen

Trong Máy ảo Ethereum(EVM), hàm băm Keccak được sử dụng rộng rãi trong việc xây dựng và xác minh cây trạng thái (Cây Merkle Patricia), chiếm phần lớn chi phí tính toán trong Bằng chứng không tri thức. Cách chứng minh Keccak hiệu quả là một vấn đề kỹ thuật chưa có lời giải từ lâu trong lĩnh vực Bằng chứng không tri thức.
Để giải quyết thách thức này, đội ngũ Polyhedra đã giới thiệu Binary GKR, một hệ thống chứng minh hiệu suất cao được thiết kế cho Keccak và các phép toán nhị phân khác.
Tiến trình cốt lõi: Tốc độ chứng minh Keccak tăng 5,7 lần
Binary GKR đạt được hiệu suất Bằng chứng không tri thức Keccak nhanh nhất cho đến nay, nhanh hơn khoảng 5,7 lần so với giải pháp tối ưu của hệ thống chứng minh nhị phân hiện tại FRI-Binius. Đột phá này không chỉ có ý nghĩa to lớn về mặt lý thuyết mà còn mở ra nhiều khả năng mới cho các ứng dụng thực tế.
Triển vọng ứng dụng: “xe đẩy tăng tốc đa năng” của zkEVM
Chúng tôi cho rằng Binary GKR có thể đóng vai trò là “sidecar tăng tốc toàn cầu” trong nhiều kiến trúc zkEVM, xử lý hiệu quả lượng lớn các hoạt động Keccak trong cây trạng thái Ethereum, do đó giảm đáng kể chi phí chứng minh và cải thiện thông lượng hệ thống cũng như tốc độ phản hồi.
Polyhedra sẽ tiếp tục thúc đẩy quá trình sản xuất và mã nguồn mở của Binary GKR, cho phép nâng cấp kiến trúc zk trong Ethereum và hệ sinh thái rộng lớn hơn.
Keccak: Chén Thánh của Ethereum
Ethereum đang dần phát triển theo hướng Bằng chứng không tri thức. Dự án Ethproofs , bao gồm 21 đội ngũ và triển khai 22 ZK(E)VM, đang cố gắng chứng minh đầy đủ các khối lịch sử Ethereum , tiến thêm một bước quan trọng.
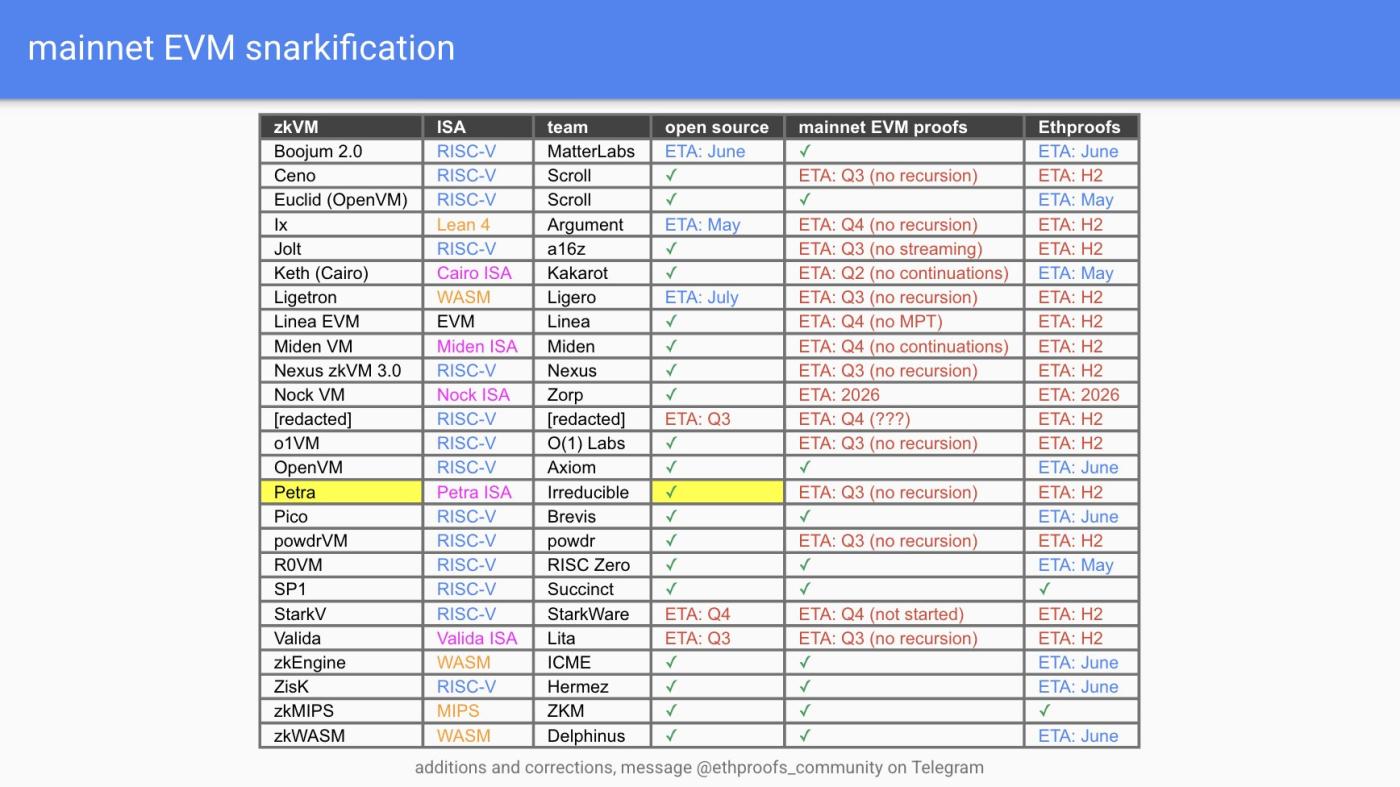
Trên trang web chính thức của Ethproofs, bạn có thể xem tiến độ của nhiều đội ngũ theo thời gian thực: các dự án như ZkCloud, Succinct, Snarkify và ZKM đã bắt đầu liên tục gửi bằng chứng ZK cho các khối mới nhất. Mục tiêu cuối cùng của xu hướng này là Ethereum thành một lớp thực thi được thúc đẩy bởi Bằng chứng không tri thức, trong khi lớp đồng thuận chỉ cần hoàn thành nhiệm vụ nhẹ như đề xuất danh sách giao dịch.
Thách thức lớn nhất mà kiến trúc zkEVM phải đối mặt: Nút thắt hiệu quả bằng chứng của Keccak
Hiện tại có nhiều dự án zkRollup tương thích với Ethereum(như Polygon, Taiko và Scroll) đang cố gắng triển khai zkEVM. Tuy nhiên, một số hoạt động trong EVM truyền thống có hiệu quả trên CPU lại tốn kém trong các hệ thống Bằng chứng không tri thức. Nút thắt trong đó về hiệu suất là hàm băm Keccak.
Keccak được sử dụng rộng rãi để xây dựng Cây Merkle Patricia của Ethereum, nơi ghi lại toàn bộ trạng thái Chuỗi dưới dạng băm. Tuy nhiên, các hoạt động cơ bản của Keccak dựa trên các hoạt động cấp bit, không tương thích với mô hình hoạt động trường chính được hầu hết các hệ thống ZK sử dụng, dẫn đến hiệu suất giảm đáng kể.
Để giúp hiểu tại sao hàm băm Keccak về cơ bản là một tập hợp các "phép toán bit", chúng tôi sẽ trình bày tóm trong đó năm phép toán cốt lõi: θ (theta), ρ (rho), π (pi), χ (chi) và ι (iota). Các phép toán này được áp dụng cho cấu trúc ma trận 5 × 5, trong đó mỗi ô là một số nguyên 64 bit, mà chúng ta gọi là một "từ". Toàn bộ ma trận có 5 hàng và 5 cột.
θ (Theta): Đầu tiên, giá trị chẵn lẻ của mỗi cột được tính toán, sau đó giá trị chẵn lẻ được phân tích loại trừ với cột liền kề bên trái; đồng thời, cột liền kề bên phải được xoay sang trái và sau đó được loại trừ. Quá trình này bao gồm các phép toán nhị phân cơ bản như "XOR" và "xoay trái".
ρ (Rho): Xoay từng từ trong ma trận sang trái từng bit một. Khoảng cách xoay của mỗi từ là khác nhau, nhưng tất cả đều là giá trị cố định được cài đặt sẵn. Bước này bao gồm toàn bộ các thao tác "bên trái".
π (Pi): Sắp xếp lại các từ trong ma trận theo một mẫu cố định. Vì quá trình này chỉ là một hoán vị vị trí nên nó thường được coi là "hoạt động không tốn chi phí" trong Bằng chứng không tri thức.
χ (Chi): Thực hiện các phép toán kết hợp bit theo từng hàng và mỗi từ sẽ được kết hợp với hai từ liền kề ở bên trái và bên phải trong hàng. Các phép toán bao gồm "loại trừ hoặc", "phủ định" và "và".
ι (Iota): Thực hiện phép toán XOR trên từ đầu tiên trong ma trận có hằng số cố định, chỉ bao gồm phép toán "XOR".
Thách thức chính khi triển khai Keccak trong Bằng chứng không tri thức là làm thế nào để biểu diễn hiệu quả các hoạt động ở cấp độ bit này, đặc biệt là khi mỗi hoạt động đều chạy trên số nguyên 64 bit. Đây là lý do tại sao chúng tôi gọi nó là Keccak-1600—vì không gian trạng thái cho mỗi vòng là 5 × 5 × 64 = 1600 bit. Quá trình hoạt động này cần phải được lặp lại 24 lần.
Tiếp theo, chúng tôi sẽ tóm tắt lại một số nỗ lực trước đây nhằm triển khai Keccak.
Nỗ lực 1: Hệ thống chứng minh dựa trên Groth 16 hoặc R 1 CS khác
Hiện nay, cách phổ biến và trực tiếp nhất là sử dụng Groth 16 hoặc các hệ thống chứng minh R 1 CS (Rank-1 Constraint System) khác để triển khai Keccak. Để thể hiện các phép toán bitwise trong Groth 16, chúng tôi biểu diễn mỗi bit là 0 hoặc 1 và mô phỏng các phép toán logic sau thông qua các mối quan hệ số học:
Phép loại trừ-hoặc: Sử dụng biểu thức a + b − 2 ab
Phủ định: Sử dụng biểu thức 1 − a (thường được tự do kết hợp vào các ràng buộc khác)
Và: Sử dụng biểu thức a × b
Tuy nhiên, các hoạt động như xoay trái và các hoạt động hoán vị khác thường được coi là hoạt động miễn phí trong hoàn cảnh ZK và không yêu cầu thêm ràng buộc nào.
Theo tính toán, số ràng buộc ở mỗi vòng Keccak như sau:
Phép toán Theta tạo ra khoảng 4480 ràng buộc
Các phép toán ρ và π là "chi phí bằng 0"
Hoạt động χ tạo ra khoảng 3200 ràng buộc
Hoạt động này tạo ra khoảng 64 ràng buộc
Do đó, một Keccak-1600 đầy đủ (24 viên đạn) sẽ tạo ra 185.856 ràng buộc trong Groth 16.
Tham khảo dữ liệu trong thư viện ICICLE của Ingonyama, mất khoảng 30-40 mili giây để tạo bản chứng minh Keccak ZK trên GPU Nvidia 4090 và khoảng 450 mili giây trên CPU. Nếu cần chứng minh hoạt động lần Keccak, GPU sẽ mất ít nhất 250 đến 300 giây, trong khi CPU có thể mất gần một giờ.
Nỗ lực 2: Hệ thống chứng minh dựa trên tra cứu
Một cách tối ưu hóa hiện đại hơn là xử lý dữ liệu theo từng đợt (ví dụ: nhóm 4 hoặc 8 bit) và thực hiện tất cả các hoạt động bit thông qua bảng tra cứu. Nói cách khác, mỗi số nguyên 64 bit được chia thành nhiều khối nhỏ (ví dụ: 8 khối 8 bit), sau đó một bảng tra cứu được sử dụng để thực hiện phép toán logic.
Cụ thể có các bảng tra cứu sau:
Bảng tra cứu XOR: Bảng tra cứu 2 ⁸ × 2 ⁸ được sử dụng để tính toán giá trị XOR của hai khối 8 bit. Điều này cho phép thực hiện XOR 8 bit với một ràng buộc thay vì 8 ràng buộc truyền thống.
Bảng tra cứu phép toán AND: Đây cũng là bảng tra cứu 2 ⁸ × 2 ⁸, được sử dụng cho phép toán AND từng bit của hai khối 8 bit. Hiệu ứng của việc lưu ràng buộc tương tự như XOR.
Bảng tra cứu xoay trái: Để xử lý thao tác xoay trái thường xuyên xảy ra trong Keccak, nhiều bảng tra cứu đã được giới thiệu. Cụ thể: bảy bảng tra cứu có kích thước 2⁸, tương ứng với khoảng cách quay là 8k+1, 8k+2, v.v. (trong đó k là số nguyên không âm). So với Nỗ lực 1, không xử lý phép quay nào cả, cách tiếp cận này tạo ra thêm chi phí chung—khoảng 192 ràng buộc bổ sung cho mỗi vòng. Tuy nhiên, so với các bộ phận khác thì chi phí này vẫn tương đối nhỏ.
Để triển khai hệ thống này, chúng tôi không còn sử dụng Groth 16 nữa mà phù hợp hơn với các hệ thống chứng minh miền nhỏ như Stwo và Plonky 3, có hỗ trợ hoàn thiện hơn cho bảng tra cứu. Theo lược đồ này, lần hoạt động Keccak hoàn chỉnh cần khoảng 27.264 ràng buộc và khi kết hợp với lệnh gọi bảng tra cứu, tổng số ràng buộc có thể giảm đáng kể, đây là một sự tối ưu hóa đáng kể so với Groth 16.
Tuy nhiên, việc tối ưu hóa này không hoàn toàn mang lại hiệu suất vượt trội. Do việc gọi và quản lý bảng tra cứu cũng gây tốn kém, nếu không được xử lý đúng cách, nó có thể làm mất đi những lợi thế do việc giảm số lượng ràng buộc mang lại. Do đó, hiệu quả hoạt động thực tế của nó có thể không tốt bằng việc triển khai dựa trên Groth 16 trong một số trường hợp.
Lần thử thứ 3: Binius
Vì tốc độ tăng tốc do bảng tra cứu hoặc cổng tùy chỉnh mang lại có thể không tốt như mong đợi trong thực tế, vì chi phí phát sinh của bản thân việc tra cứu có thể bù đắp cho hiệu ứng tối ưu hóa ràng buộc, nên chúng ta cần khám phá những con đường khác để cải thiện hiệu quả của các bằng chứng Keccak.
Đây là lý do tại sao Keccak được mệnh danh là "chén thánh của kiến thức bằng không". So sánh mà nói, các hàm băm ban đầu như SHA-256 và Blake 2/3 cũng dựa vào các phép toán bit như XOR và AND, nhưng điểm yếu lớn nhất về hiệu suất của chúng lại đến từ phép cộng số nguyên. Phép cộng số nguyên thường được tối ưu hóa trong các hệ thống chứng minh bằng cách chia nó thành nhiều khối 4 bit, giúp cải thiện hiệu suất đáng kể. Nhưng Keccak không liên quan đến phép cộng số nguyên nào nên các chiến lược tối ưu hóa này không hiệu quả ở đây.
Giải pháp tiên tiến nhất hiện nay là Binius. Ý tưởng cốt lõi của hệ thống là vì Keccak được tạo thành hoàn toàn từ các phép toán bit nên chúng ta có thể triển khai nó bằng cách sử dụng hệ thống chứng minh dựa trên bit. Đây chính là lúc Binius đột phá.
Trong Binius, Keccak được biểu diễn như một phép toán trên trường hữu hạn 𝐹₂, đây là trường nhị phân. Vì XOR về cơ bản chỉ là phép cộng trong 𝐹₂, nên chi phí liên quan đến nó gần như được loại bỏ hoàn toàn. Toàn bộ quá trình được cấu trúc như sê-ri các phép toán đa thức và các phép toán xoay bit cũng có thể dễ dàng được triển khai trong mô hình xử lý từng bit. Thực tế thì chi phí chủ yếu tập trung ở các cổng AND xuất hiện trong bước x.
Bài kiểm tra chuẩn của Binius cho thấy chỉ mất khoảng 12,35 giây để chứng minh lần phép toán Keccak, tốt hơn nhiều so với Groth 16 (lần thử 1) và phương pháp bảng tra cứu (lần thử 2).
Binius có phải là kết thúc không? Thực tế thì không phải như vậy. Chúng tôi nhận thấy rằng bằng cách loại bỏ một số phần dư thừa trong bằng chứng Keccak, có thể cải thiện hiệu suất thêm khoảng năm lần so với triển khai Binius hiện tại.
Polyhedra ra mắt Binary GKR: Hệ thống chứng minh nhị phân được tối ưu hóa cho Keccak
Đội ngũ Polyhedra đang xây dựng một hệ thống chứng minh mới - Binary GKR (xem: ePrint 2025/717 ), đây là một khuôn khổ dành riêng cho việc chứng minh hiệu quả các phép toán nhị phân, đặc biệt phù hợp với các hàm như Keccak tập trung vào các phép toán bit. Những lợi thế cốt lõi của Binary GKR đến từ ba cải tiến công nghệ quan trọng sau đây:
1. Tối ưu hóa các phép tính lặp lại dựa trên giao thức GKR
Chúng tôi chọn thiết kế Binary GKR dựa trên giao thức GKR (Goldwasser–Kalai–Rothblum) vì nó có thể giảm hiệu quả chi phí dư thừa phát sinh do xử lý các phép tính lặp đi lặp lại.
Trong một kịch bản zkEVM điển hình, Keccak thường xuất hiện như nhân vật " Prover sidecar" để xử lý hàng loạt lượng lớn nhiệm vụ tính toán Keccak được zkEVM giao phó. Do đó, các cấu trúc mạch mà chúng tôi nhắm tới thường có lượng lớn các mẫu lặp lại, ví dụ: lần cuộc gọi Keccak có kích thước phổ biến.
Quan trọng hơn, thuật toán Keccak có khả năng tái tạo cao:
Nó thực hiện lặp đi lặp lại các phép toán Boolean tương tự trên ma trận trạng thái 5 × 5;
Toàn bộ quá trình bao gồm 24 vòng với các bước gần như giống hệt nhau;
Cấu trúc của mỗi vòng đều giống nhau, chỉ có trạng thái đầu vào là khác nhau.
Những đặc điểm như vậy khiến Keccak trở thành "người thích nghi tự nhiên" với giao thức GKR:
Thiết bị xác minh có chi phí thấp và phù hợp với các tình huống xác minh tần suất cao;
Prover có thể tận dụng tối đa tính lặp lại của cấu trúc, tái sử dụng các đường dẫn tính toán và đơn giản hóa đáng kể chi phí chứng minh;
So với các hệ thống chứng minh chung truyền thống, nó có lợi thế đáng kể về hiệu suất trong các tình huống Keccak hàng loạt.
2. Cam kết đa thức dựa trên trường nhị phân
Chúng tôi sử dụng sơ đồ cam kết đa thức dựa trên mã tuyến tính hoạt động trực tiếp trên trường nhị phân. Như đã đề cập trước đó, việc sử dụng biểu diễn nhị phân gốc cho phép chúng ta thực hiện các phép toán như XOR "miễn phí". Ngoài ra, tương tự như phương pháp của Binius, cam kết đa thức dựa trên trường nhị phân tránh được sự dư thừa do sử dụng trường số lớn hơn, giúp cải thiện đáng kể hiệu suất và hiệu quả của hệ thống.
3. Bảng tính toán trước cho các phép toán nhị phân
Đổi mới chính trong bài báo Binary GKR là hiệu quả chứng minh của giao thức GKR được cải thiện đáng kể bằng cách tận dụng tối đa tính thưa thớt cao của cấu trúc mạch. Sự thưa thớt này vẫn được duy trì ngay cả khi xử lý nhiều bit cùng lúc. Những gì chúng tôi làm là "gói" nhiều bit thành các đa thức trong giao thức GKR (lưu ý: đây là các đa thức trung gian và không yêu cầu cam kết), sau đó thực hiện các hoạt động giao thức GKR trực tiếp trên dữ liệu được đóng gói này.
Do độ thưa thớt vẫn còn cao, chúng ta có thể tận dụng các bảng tính toán trước để cho phép người chứng minh tạo ra các bằng chứng với chi phí tính toán ít hơn nhiều so với giao thức GKR truyền thống. Việc tối ưu hóa này cải thiện đáng kể hiệu quả của GKR khi xử lý các mối quan hệ nhị phân.
Bài viết này sẽ tập trung vào phương pháp tối ưu hóa kỹ thuật thứ ba được đề cập ở trên: bảng tính toán trước cho các phép toán nhị phân.
Đóng gói các bit vào đa thức
Cốt lõi của chương trình của chúng tôi là phương pháp kiểm tra tổng mới cho giao thức GKR được thiết kế riêng cho mạch Boolean song song dữ liệu . Phương pháp này làm giảm đáng kể gánh nặng tính toán của trình chứng minh và cải thiện hiệu quả đáng kể bằng cách đóng gói nhiều bit vào một đa thức.

Đánh giá các mối quan hệ nhị phân hiệu quả hơn
So với GKR truyền thống, Binary GKR mang đến không gian tối ưu hóa mới.


Bảng tiền xử lý này rất nhỏ. Bằng cách thiết lập các thông số phù hợp, chúng ta có thể giữ kích thước bảng ở mức khoảng 15 MB. Kích thước này vừa vặn với bộ nhớ đệm L3 của CPU, giúp cho hoạt động tra cứu bảng trở nên rất hiệu quả.
Kỹ thuật này có thể áp dụng cho hầu hết các phép toán nhị phân và là cốt lõi của việc cải thiện hiệu suất trong cấu trúc Binary GKR.
Thực hiện và Đánh giá
Chúng tôi đã triển khai hệ thống SNARK trong Rust dựa trên hệ sinh thái arkworks và tiến hành đánh giá chuẩn toàn diện trên các mạch Boolean ngẫu nhiên có kích thước khác nhau.
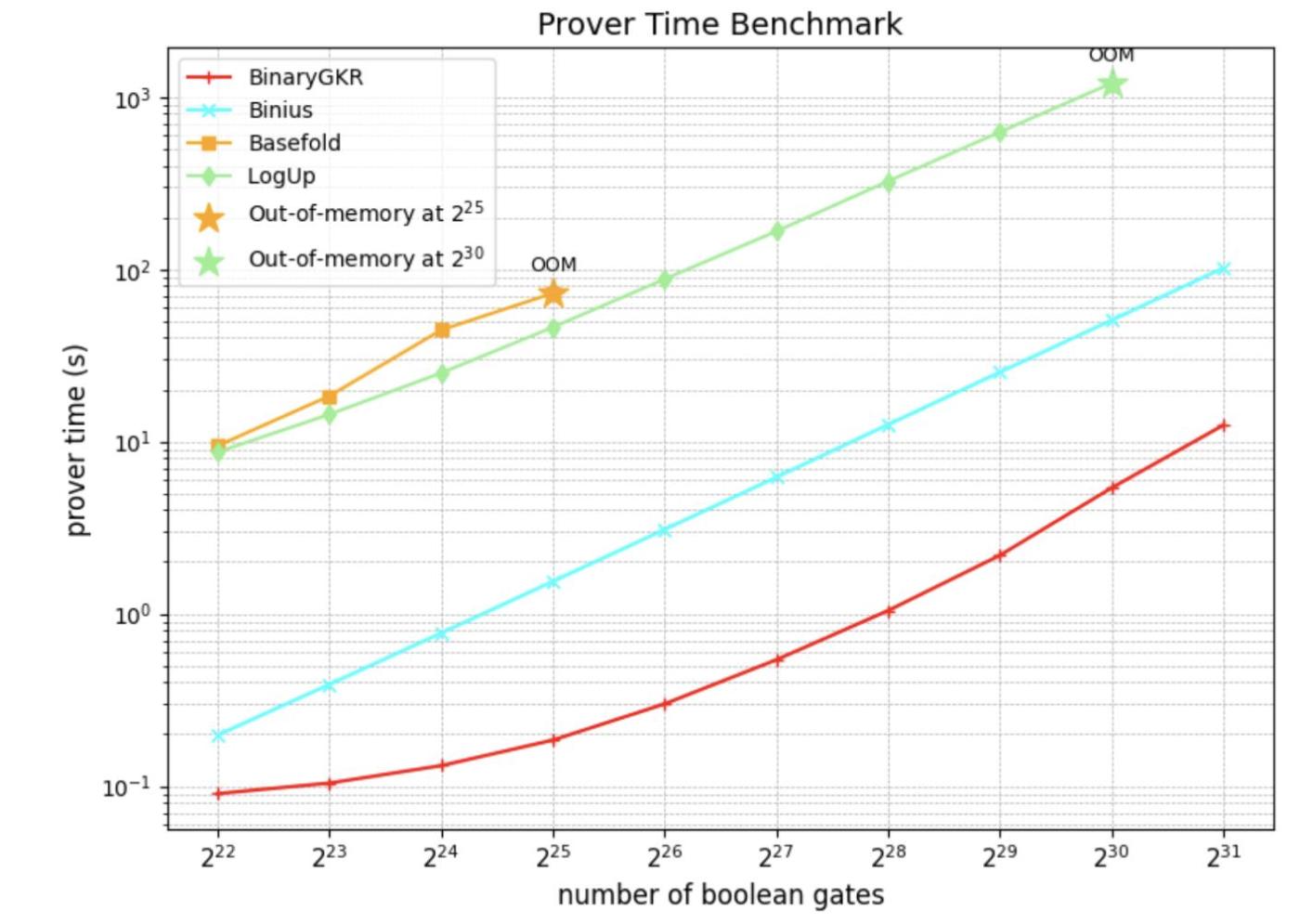
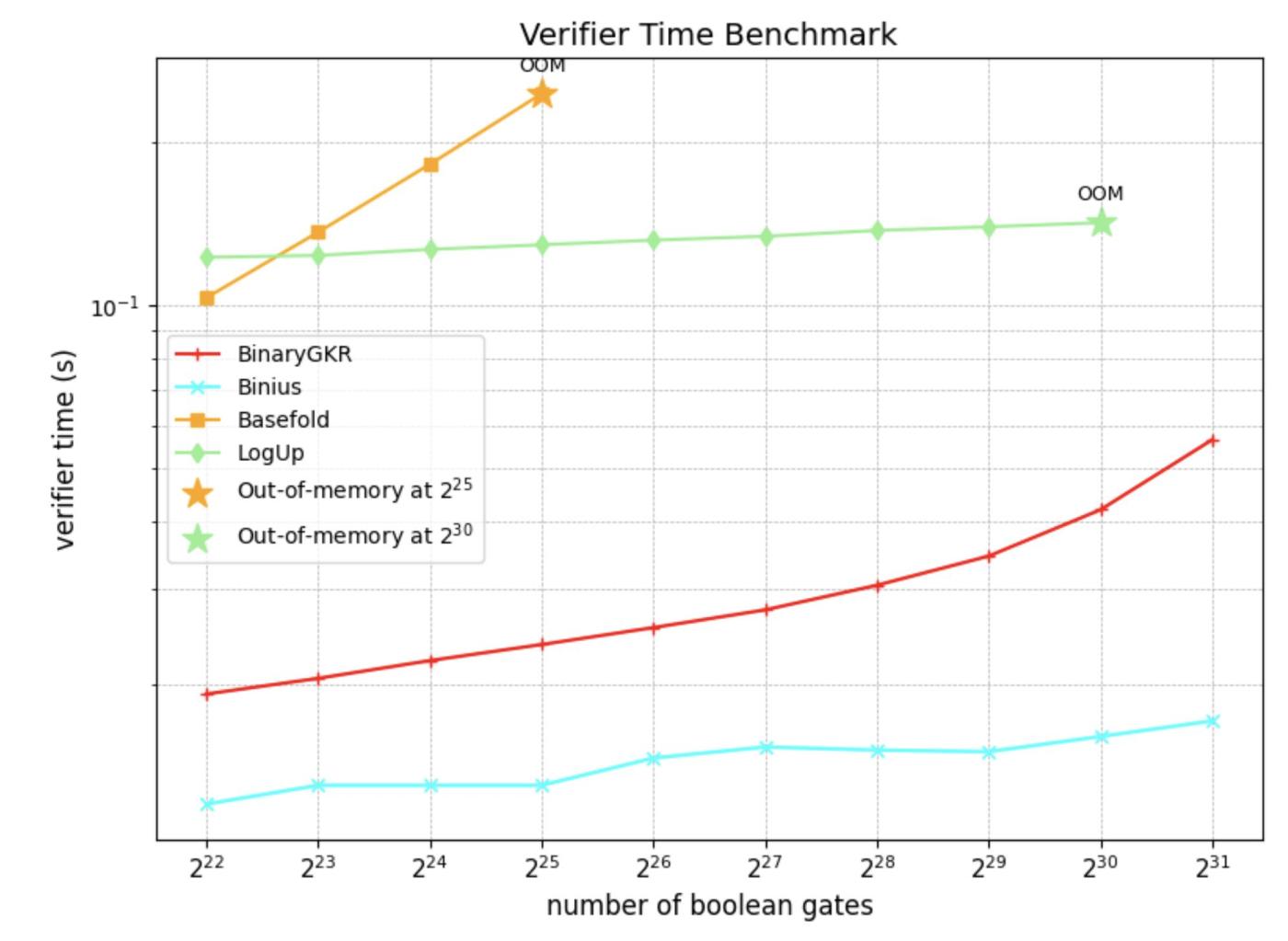
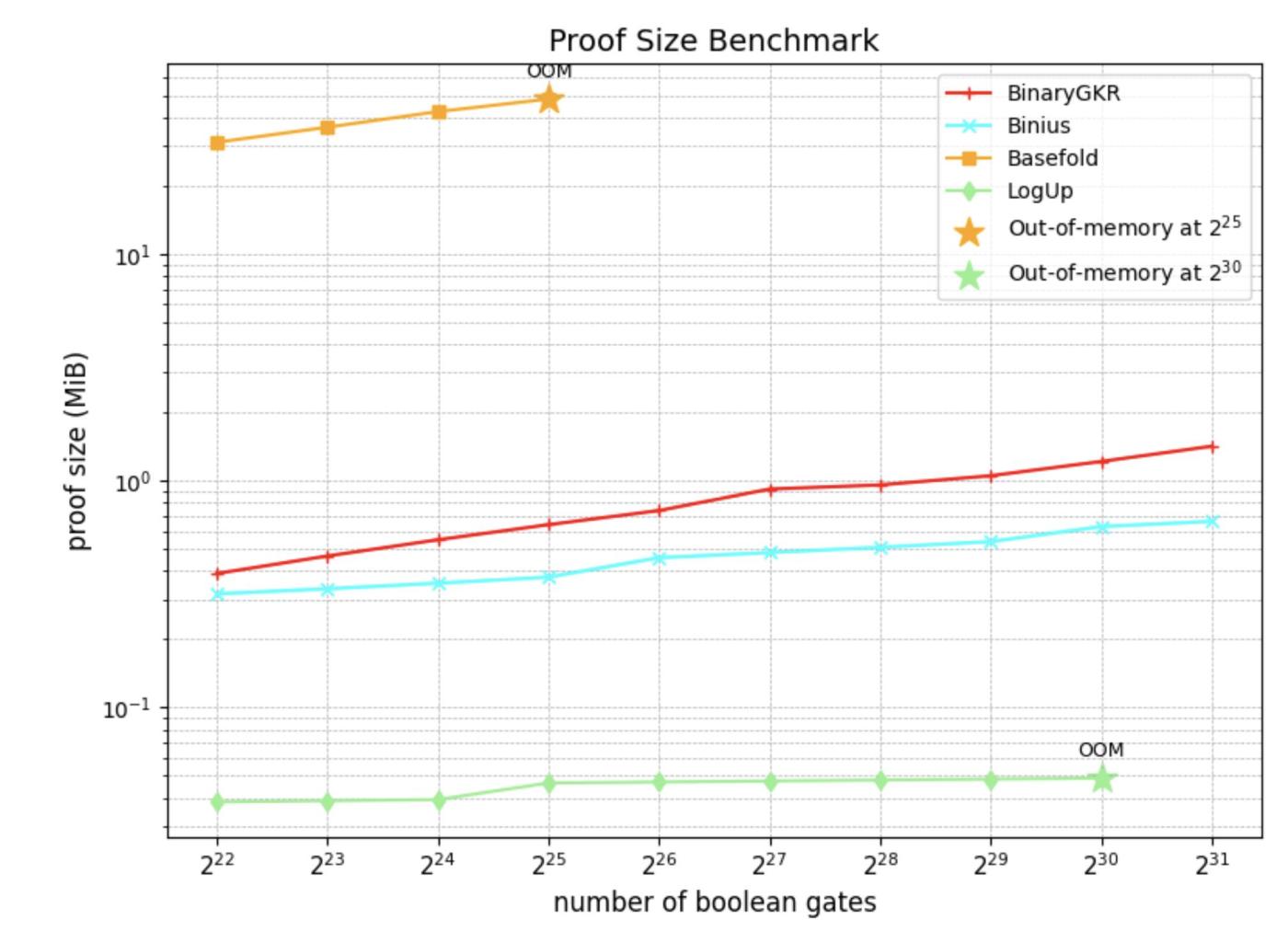
Ngoài các mạch Boolean ngẫu nhiên, chúng tôi cũng tập trung vào "chén thánh" của Bằng chứng không tri thức- Keccak. Chúng tôi so sánh hiệu suất của phương pháp đề xuất với Binius trên bằng chứng Keccak. Cả hai đều dựa trên phép toán miền nhị phân.
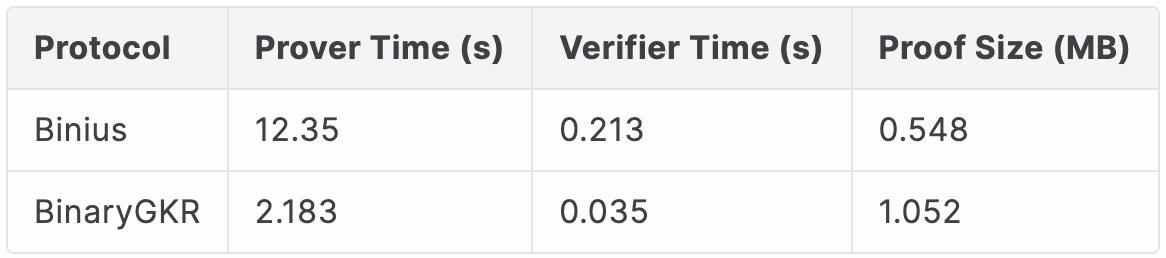
Khi xử lý lần lệnh gọi Keccak, Binius mất 12,35 giây để tạo bằng chứng, trong khi phương pháp của chúng tôi chỉ mất 2,18 giây. Đồng thời, nhờ cấu trúc ngắn gọn của Keccak nên thời gian xác minh của chúng tôi cũng ngắn hơn, chỉ 0,035 giây. Xét về chi phí truyền thông, kích thước bản in thử của chúng tôi là 1,052 MB.
Phần kết luận
Bài viết này trình bày tiến triển mới nhất của đội ngũ Polyhedra trong lĩnh vực Bằng chứng không tri thức , tập trung vào tối ưu hóa cho các hàm nhị phân như Keccak. Thành tựu này có thể được sử dụng như một " mô-đun phụ trợ" hiệu quả để xây dựng nhiều loại zkEVM khác nhau.
Chúng tôi có kế hoạch tích hợp Binary GKR vào các hệ thống zkEVM như RISC Zero và SP 1 để xác minh thêm vai trò của nó trong việc giảm thiểu tình trạng tắc nghẽn hiệu suất của Keccak. Mục tiêu cuối cùng là đẩy nhanh tiến độ Ethereum hướng tới SNARK hóa hoàn toàn lớp 1 mà không phá hủy kiến trúc EVM hiện có.
Liên kết gốc: https://blog.polyhedra.network/binary-gkr/






