Về việc khuyến khích sự tham gia ẩn danh

avatar
Ethereum Research
05-27
Bài viết này được dịch máy
Xem bản gốc

Về việc khuyến khích sự tham gia ẩn danh

tải lên_0bca3fb7f6b0d2fc3fe0596f28531112
upload_0bca3fb7f6b0d2fc3fe0596f28531112 1300×867 189 KB

\cdot ⋅
tl;dr; Hoạt động blockchain được tạo điều kiện thuận lợi thông qua các tác nhân độc lập tham gia vào các giao thức được chia sẻ. Việc khuyến khích sự tham gia này là một cân nhắc thiết kế quan trọng, đặc biệt là trong các môi trường không cần xin phép, đối đầu và ẩn danh. Chúng tôi trình bày một mô hình và thúc đẩy trò chơi tham gia trong Phần 1. Trong Phần 2 , chúng tôi phân tích các trạng thái cân bằng đối xứng, ẩn danh của trò chơi này. Sau đó, chúng tôi áp dụng khuôn khổ này trong hai cài đặt. Phần 3 trình bày chi tiết về thị trường chứng minh, nhằm mục đích khuyến khích việc tạo ra ít nhất một bằng chứng . Phần 4 chuyển sang các giao thức Bằng chứng công việc, nhằm mục đích khuyến khích ít nhất 50% sự tham gia (được thúc đẩy bởi mục tiêu tránh cuộc tấn công 51%). Trong cả hai trường hợp, chúng tôi đưa ra cấu trúc khuyến khích tối ưu cho giao thức để giảm thiểu chi phí của nó. Chúng tôi kết luận trong Phần 5 bằng cách thảo luận về cách mô hình có thể được mở rộng và các kỹ thuật cụ thể khác của blockchain được sử dụng để khởi động sự tham gia.
\cdot ⋅
bởi maryam & mike – ngày 26 tháng 5 năm 2025.
\cdot ⋅
Cảm ơn Akilesh , Noam , Matt và Barnabé đã đánh giá và thảo luận về bài đăng này!

Nội dung

(1). Động cơ & Mô hình
(1.1). Mô hình trò chơi tham gia
(1.2). Một giải pháp tầm thường, không ẩn danh
(1.3). Một trạng thái cân bằng không đối xứng
(2). Cân bằng đối xứng của quy tắc thanh toán xổ số
(2.1). Xét n n lớn
(3). Giảm thiểu chi phí thị trường thử nghiệm
(3.1). Tối ưu hóa cho ít nhất một người tham gia
(3.2). Tiệm cận
(3.3). 1 + \ln c 1 + ln c ràng buộc là chặt chẽ
(4). Một hàm mục tiêu Bằng chứng công việc
(4.1). Tiệm cận
(5). Kết luận và công việc tương lai
(5.1). Các hàm chi phí thay thế
(5.2). Các tác nhân không đồng nhất và thông tin bất đối xứng
(5.3). Mã thông báo, airdrop và ứng dụng blockchain

1. Động lực & Mô hình

Đoạn mở đầu – Bạn đang ở quán bar thể thao địa phương và có một chiếc bàn để xem một trận playoff NBA. Bạn không muốn xem một mình, vì vậy bạn dự định cho nhóm trò chuyện biết bạn đang ở đó. Để mọi người có nhiều khả năng đến hơn, bạn đề nghị mua một suất cánh gà đầu tiên, nhưng trước tiên bạn cần quyết định số lượng sẽ gọi. Nếu bạn gọi quá ít, có khả năng sẽ không có ai đến, nghĩ rằng sẽ có người khác đến và sẽ không có đủ cho mọi người. Nếu bạn gọi quá nhiều, sẽ không có chỗ ở bàn nếu mọi người đều đến. Số lượng cánh gà tối ưu để mua là bao nhiêu để một số người bạn của bạn đến, nhưng không phải tất cả? 1

Câu chuyện này thường xuất hiện trong thiết kế giao thức blockchain. Các giao thức muốn thu hút sự tham gia dưới một hình thức nào đó và sử dụng các ưu đãi để tạo ra sự tham gia đó:

  • Proof-of-Work cung cấp phần thưởng khối để khuyến khích thợ đào giải các câu đố mật mã.
  • Proof-of-Stake cung cấp phần thưởng đồng thuận cho việc đặt cược và bỏ phiếu đúng trên các khối.
  • Thị trường Prover phối hợp sản xuất các bằng chứng ZK có yêu cầu tính toán chuyên sâu.

Quan trọng hơn, blockchain cũng muốn cho phép tham gia không cần xin phép . Điều này làm cho vấn đề phối hợp trở nên khó khăn hơn nhiều. Bài đăng này trình bày một mô hình để khuyến khích sự tham gia và phân tích trạng thái cân bằng đối xứng của các quy tắc thanh toán giá trị chung, ẩn danh. Cụ thể, chúng tôi nghiên cứu trạng thái cân bằng trong đó mỗi người chơi chơi chiến lược hỗn hợp là mua vé số với xác suất p p .

1.1. Mô hình trò chơi tham gia

Chúng tôi mô hình hóa trò chơi tham gia như sau:

  • người chơi – Người chơi là tác nhân chiến lược, dựa trên cơ chế, có thể chọn mua vé vào cửa.
  • người tham gia – Người tham gia là người chơi mua vé vào cửa.
  • giao thức – Giao thức là một tác nhân có hàm chi phí (hoặc tương đương, hàm định giá dương) để thúc đẩy sự tham gia.
  • quy tắc thanh toán – Một chức năng được giao thức triển khai để ánh xạ tập hợp những người tham gia vào khoản thanh toán tương ứng của họ.

Giả sử có n n người chơi trong trò chơi tham gia. Mỗi người phải đối mặt với cùng một khoản phí tham gia, q q , khiến đây trở thành một cuộc đấu giá có giá trị chung. Để đơn giản, chúng tôi sử dụng q = 1 q = 1 cho phần còn lại của bài đăng này. Mỗi người tham gia có thể quyết định tham gia hay không; họ cũng có thể chọn chơi một chiến lược ngẫu nhiên trong đó họ tham gia với một số xác suất p p . Trước khi quyết định có tham gia hay không, những người tham gia tuân thủ một quy tắc thanh toán được chỉ định trong giao thức. Quy tắc thanh toán có thể phụ thuộc vào tập hợp những người tham gia đã thực hiện và có thể được ngẫu nhiên hóa. Mỗi người tham gia chọn một hành động để tối đa hóa tiện ích mong đợi của họ, nghĩa là khoản thanh toán mong đợi họ nhận được trừ đi phí tham gia (nếu họ chọn tham gia).

Hai phần sau đây giới thiệu các khái niệm về ẩn danh và tính đối xứng.

1.2. Một giải pháp đơn giản, không ẩn danh

Giả sử giao thức này nhằm mục đích thu hút ít nhất một người tham gia và giả sử người chơi hòa có lợi cho việc tham gia. Một cơ chế đơn giản như sau: “Chọn một người chơi cụ thể, được ký hiệu là WINNER THẮNG và nói với họ rằng bạn sẽ trả cho họ 1 đô la nếu họ tham gia”. Giải pháp tầm thường này có nhiều đặc tính mong muốn:

  1. tính hợp lý cá nhân cho mọi người (vì mỗi người chơi có thể đạt được tiện ích bằng không nếu không tham gia) và
  2. sự tham gia thỏa đáng vào trạng thái cân bằng ( WINNER sẽ tham gia và không ai khác sẽ tham gia), và
  3. giảm thiểu chi phí thanh toán cho giao thức (vì 1 đô la là phí vé và do đó là chi phí nhỏ nhất có thể để có được một người tham gia).

Nếu người thiết kế giao thức đồng ý chọn người chiến thắng thì giải pháp này là đủ. 2 Thay vì dừng lại ở đây, chúng tôi tập trung vào một tập hợp các giải pháp ẩn danh.

Định nghĩa (không chính thức): Quy tắc thanh toán ẩn danh không thể phụ thuộc vào danh tính của người chơi.

Chúng tôi chính thức hóa thuộc tính này trong Mục 3.3 , nhưng hy vọng là nó sẽ trực quan. Các quy tắc thanh toán này phải đối xử bình đẳng với mọi người chơi. Các quy tắc có thể phụ thuộc vào hành động của người chơi (ví dụ, bằng cách chia đều giải thưởng cho tất cả những người tham gia) và có thể được ngẫu nhiên hóa (ví dụ, bằng cách trao giải thưởng cho một người tham gia ngẫu nhiên). Tuy nhiên, cơ chế trên dựa vào danh tính của người chơi và không ẩn danh.

1.3. Cân bằng không đối xứng

Riêng biệt, hãy xem xét tình huống sau: "Một người chơi duy nhất, được ký hiệu là COMMITTER , cam kết công khai mua vé và trở thành người tham gia". Tùy thuộc vào quy tắc thanh toán, cam kết này có thể khiến những người chơi khác không muốn tham gia. Ví dụ, giả sử quy tắc thanh toán chia đều giải thưởng là 1 đô la cho tất cả những người tham gia. Trong trường hợp đó, một người chơi thứ hai đang cân nhắc tham gia chắc chắn sẽ có tiện ích âm vì họ trả 1 đô la và kiếm được 1/2 đô la. Điều này dẫn đến không ai khác tham gia giao thức và COMMITTER kiếm được toàn bộ giải thưởng. Trạng thái cân bằng này là thanh toán tối thiểu cho giao thức nhưng yêu cầu những người tham gia phải chọn COMMITTER , đẩy sự phức tạp phối hợp cho những người chơi. Chúng tôi sử dụng ví dụ này làm động lực để hạn chế sự chú ý của mình vào các trạng thái cân bằng đối xứng .

Định nghĩa: Trong trạng thái cân bằng đối xứng, mỗi người chơi đều sử dụng cùng một chiến lược.

Chiến lược này có thể là xác định (ví dụ, luôn mua một vé và tham gia) hoặc hỗn hợp (ví dụ, mua một vé với xác suất p p ). Vì các chiến lược xác định này có thể được coi là p = 0 p = 0 hoặc p = 1 p = 1 tương ứng, nên bất kỳ trạng thái cân bằng đối xứng nào cũng được chỉ định đầy đủ bởi một giá trị duy nhất p\in[0,1] p ∈ [ 0 , 1 ] . Trong trạng thái cân bằng như vậy, số lượng người tham gia được rút ra từ \text{Binomial}(n,p) Binomial ( n , p ) , trong đó n n là số lượng người chơi.

2. Cân bằng đối xứng của quy tắc thanh toán xổ số

Khi chúng ta chỉ tập trung vào trạng thái cân bằng đối xứng, chỉ có ba kết quả cho các chiến lược của người chơi:

  1. không ai tham gia ( p = 0 p = 0 ),
  2. mọi người đều tham gia ( p = 1 p = 1 ),
  3. mọi người tham gia với xác suất p\in (0,1) p ∈ ( 0 , 1 ) .

Tùy thuộc vào quy tắc thanh toán, bất kỳ kết quả nào trong số này đều có thể xảy ra. Phần này nghiên cứu quy tắc thanh toán xổ số.

Định nghĩa: Luật thanh toán xổ số trả cho một người chơi duy nhất một giải thưởng có giá trị x x bằng cách chọn ngẫu nhiên một người chiến thắng từ nhóm người tham gia.

Quy tắc thanh toán xổ số là ẩn danh và tạo ra trạng thái cân bằng đối xứng p p tùy thuộc vào kích thước của x x . Giao thức đặt giá trị của x x , người chơi quyết định có tham gia hay không và giải thưởng được trao toàn bộ cho một trong những người tham gia. Nếu x < 1 x < 1 , chúng ta ở trong trường hợp (1); sẽ không có ai tham gia vì giải thưởng ít hơn lệ phí tham gia. Nếu x\geq n x ≥ n , thì chúng ta ở trong trường hợp (2); mọi người sẽ tham gia vì họ được đảm bảo (trong kỳ vọng) sẽ được trả nhiều hơn lệ phí tham gia của họ. Đối với các giá trị khác của x x , số lượng người tham gia sẽ là một biến ngẫu nhiên được lấy từ \text{Binomial}(n,p) Binomial ( n , p ) với p\in (0,1) p ∈ ( 0 , 1 ) . Giao thức có thể dịch chuyển giá trị trung bình, np n p , bằng cách điều chỉnh x x .

Chúng ta có thể mô tả trạng thái cân bằng đối xứng trong trường hợp (3) ở trên, trong đó mỗi người chơi kết hợp chiến lược của họ và tham gia với xác suất p p . (Có nhiều cách tiếp cận; chúng tôi trình bày cách tiếp cận rõ ràng ở đây bằng cách sử dụng phép tính vi phân; xem mục #1 để biết một phương án thay thế.) Chúng tôi xem xét quyết định của người chơi i i bằng cách sửa các chiến lược của những người chơi khác tại p p . i i chọn xác suất tham gia p' p ′ của mình để tối đa hóa tiện ích mong đợi của nó,

\begin{align}U_i(p') &= \bigg[ \underbrace{\mathbb{E}\left[\frac{x}{1+Y}\right]}_{\text{tiền thắng cược dự kiến}} - \underbrace{1}_{\text{giá vé}}\bigg] p', \; \text{trong đó } Y \sim \text{Nhị thức}(n-1,p) \\&= \left[x\cdot \frac{1-(1-p)^n}{np} -1\right]p'\end{align}
U i ( p ′ ) = [ E [ x 1 + Y ]    tiền thắng cược dự kiến − 1  giá vé ] p ′ , trong đó Y ∼ Nhị thức ( n − 1 , p ) = [ x ⋅ 1 − ( 1 − p ) n n p − 1 ] p ′

Nói cách khác, người chơi i i nhận được khoản thanh toán là x x nếu cô ấy tham gia và trúng số trong số những người tham gia. Đặc biệt, vì mỗi người chơi khác trong số n-1 n − 1 tham gia độc lập với xác suất p p , nên số người tham gia bên cạnh i i được lấy từ \text{Binomial}(n-1,p) Binomial ( n − 1 , p ) . Tiện ích của i i khi tham gia là khoản thanh toán trừ đi giá vé. Tiện ích của i i khi tham gia với xác suất p' p ′ là tiện ích của cô ấy khi tham gia nhân với p' p ′ , vì i i nhận được 0 tiện ích khi không tham gia.

Để chiến lược đối xứng p p là trạng thái cân bằng, p'=p p ′ = p phải tối đa hóa biểu thức này trong số tất cả p'\in[0,1] p ′ ∈ [ 0 , 1 ] . Điều kiện bậc nhất là

\begin{align}\frac{\partial U_i}{\partial p'} = x\cdot \frac{1-(1-p)^n}{np} -1.\end{align}
[Lỗi xử lý toán học]

Đặt giá trị này bằng 0, chúng ta sẽ có được một giải pháp phân tích cho mối quan hệ giữa x x và p p ,

x\cdot \frac{1-(1-p)^n}{np} -1 = 0\ngụ ý \boxed{x = \frac{np}{1-(1-p)^n}}
x ⋅ 1 − ( 1 − p ) n n p − 1 = 0 ⟹ x = np 1 − ( 1 − p ) n​

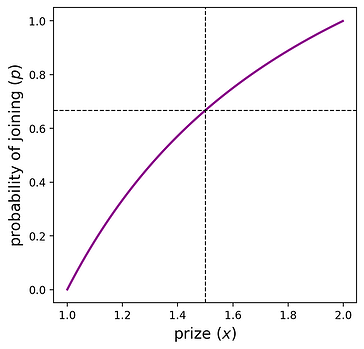
Điều này cho chúng ta biết: “nếu được trao giải thưởng có giá trị x x , thì xác suất p p tạo ra trạng thái cân bằng đối xứng là bao nhiêu” hoặc tương đương, “nếu nhà thiết kế giao thức muốn số lượng người tham gia đến từ \text{Binomial}(n,p) Binomial ( n , p ) , họ sẽ đặt giải thưởng có giá trị x x .” Biểu đồ bên dưới cho thấy mối quan hệ giữa các biến này đối với n = 2 n = 2 .

tải lên_d625b6de301ed0283341dc168f71222a
upload_d625b6de301ed0283341dc168f71222a 931×895 37,7 KB

Các đường đứt nét được diễn giải là, “nếu giao thức đặt giải thưởng x=1,5 x = 1,5 , thì chiến lược p=2/3 p = 2 / 3 là trạng thái cân bằng đối xứng”. Ngoài ra, hãy lưu ý rằng nếu giải thưởng là <1 < 1 hoặc >2 > 2 , thì người chơi tham gia với xác suất tương ứng là 0 hoặc 1. Đây là kết quả “không ai tham gia” và “mọi người đều tham gia” được mô tả ở đầu phần này. Đối với vùng bên trong, x \in (1,2) x ∈ ( 1 , 2 ) , thì một p p duy nhất được tạo ra bởi mỗi x x .

Ngoại lệ số 1 Một cách khác để suy ra cùng một phương trình là bằng cách xem xét dòng tiền tổng hợp cho tập hợp tất cả người chơi. Đối với một p p cho trước, tập hợp người chơi trả np n p phí tham gia dự kiến. Do đó, giao thức sẽ cần phải trả np n p theo kỳ vọng dưới dạng hoàn trả (vì đây là trạng thái cân bằng cạnh tranh, bất kỳ giá trị vượt mức nào cũng sẽ bị cạnh tranh loại bỏ). Khi giao thức chọn giải thưởng x x , tập hợp người chơi sẽ nhận được giải thưởng này miễn là có ít nhất một người chơi tham gia . Điều này xảy ra với xác suất 1-(1-p)^n 1 − ( 1 − p ) n , nghĩa là tập hợp người chơi kiếm được x \cdot (1-(1-p)^n) x ⋅ ( 1 − ( 1 − p ) n ) phần thưởng.

Ngoại lệ #2: Một đặc tính thú vị của cân bằng chiến lược hỗn hợp là người chơi không quan tâm đến bất kỳ hành động nào (đó là lý do tại sao họ ngẫu nhiên hóa hành vi của mình ngay từ đầu). Trong ví dụ trên, nếu mọi người khác tham gia với xác suất p p , người chơi i i nhận được tiện ích bằng không từ bất kỳ hành động nào. Bạn có thể thấy điều này bằng cách thay x x vào hàm tiện ích của cô ấy,

\begin{align}U_i(p') &= \bigg[ x \cdot \frac{1-(1-p)^n}{np} -1\bigg] \cdot p' \\&= \bigg[\frac{np}{1-(1-p)^n}\cdot \frac{1-(1-p)^n}{np} -1\bigg] p' \\&= (1-1)p'\\&= 0.\end{align}
[Lỗi xử lý toán học]

Một cách khác để diễn giải điều này là trạng thái cân bằng là hoàn toàn cạnh tranh. Điều này gây ra sự thờ ơ giữa kết quả và chiến lược hỗn hợp kết quả.

2.1 Xét n n lớn

Nhắc lại mối quan hệ

x = \frac{np}{1-(1-p)^n}.
x = np 1 − ( 1 − p ) n​ .

Một quan sát thú vị về phương trình này là, đối với n n lớn, chúng ta có thể viết lại x x dưới dạng hàm của \mu=np μ = n p (số lượng người tham gia dự kiến), sử dụng (1-x) \rightarrow e^{-x} ( 1 − x ) → e − x đối với x x nhỏ như

x(\mu) \approx \frac{\mu}{1-e^{-\mu}}.
x ( μ ) ≈ μ 1 − e − μ .

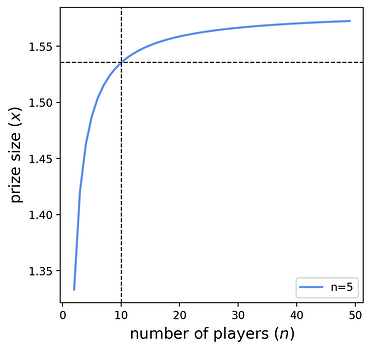
Giao thức có thể nhắm mục tiêu số lượng người tham gia trung bình mong muốn \mu μ bằng cách sử dụng công thức đơn giản này, mà không cần biết n n . Ví dụ, nếu giao thức muốn có một người tham gia duy nhất trong kỳ vọng, thì giao thức sẽ đặt giải thưởng là 1/(1-1/e)\approx 1.582 1 / ( 1 − 1 / e ) ≈ 1.582 . Nghĩa là, giao thức trả mức phí bảo hiểm 58\% 58 % so với phí tham gia là 1 1 để thu hút một người tham gia trong kỳ vọng. Xấp xỉ này được cải thiện khi n n tăng lên. Biểu đồ bên dưới hiển thị giải thưởng giao thức cần thiết để thu hút một người tham gia trung bình. Nó cũng hiển thị giới hạn khi n \to \infty n → ∞ tiến tới x(1)=1/(1-1/e) x ( 1 ) = 1 / ( 1 − 1 / e ) .

tải lên_9cde4a87098e4108fb332832c204d531
tải lên_9cde4a87098e4108fb332832c204d531 949×895 33,3 KB

Các đường đứt nét có thể được hiểu là: “nếu n = 10 n = 10 , thì nhà thiết kế giao thức cần đặt giải thưởng ít nhất là x = 1,535 x = 1,535 để thu hút một người tham gia theo kỳ vọng”. Tất nhiên, nhà thiết kế giao thức có thể chọn giải thưởng cao hơn để giảm rủi ro không có người tham gia. Phần sau đây mô tả sự đánh đổi này một cách chính thức.

3. Giảm thiểu chi phí thị trường Prover

Cho đến nay, chúng tôi đã chỉ ra cách giao thức có thể nhắm mục tiêu vào số lượng tham gia dự kiến cụ thể, \mu μ , bằng cách thay đổi x x . Bây giờ chúng tôi xem xét các giao thức đặc biệt không thích sự tham gia thấp. Chúng tôi chính thức hóa điều này bằng cách giới thiệu "hình phạt tham gia thấp". Trong phần này, chúng tôi bắt đầu bằng cách kiểm tra các thị trường chứng minh. Trong Phần 4 , chúng tôi sẽ xem xét một hình phạt tham gia thấp khác được thúc đẩy bởi sự đồng thuận Bằng chứng công việc.

Chúng tôi xem xét một ZK rollup muốn khuyến khích việc sản xuất bằng chứng tốn kém. Nhà thiết kế thị trường chỉ có thể quan tâm đến việc có ít nhất 1 người chứng minh tham gia (và trả phí tham gia, tức là chi phí tạo ra bằng chứng). 3 Hơn nữa, giả sử nếu không có sự tham gia nào cả, giao thức có thể tự tạo bằng chứng với chi phí là c c (bạn có thể coi c c là "tùy chọn bên ngoài"). Điều này cho phép chúng ta viết hình phạt tham gia thấp dưới dạng hàm số của số lượng người tham gia, k k , như

\begin{align}\text{hình phạt tham gia thấp}(k) =\begin{cases}c & \text{nếu } k = 0 \\0 &\text{nếu không}.\end{cases}\end{align}
[Lỗi xử lý toán học]

Đương nhiên, người thiết kế giao thức muốn chọn quy tắc thanh toán giúp giảm thiểu tổng chi phí (quy mô giải thưởng cộng với bất kỳ hình phạt nào).

3.1. Tối ưu hóa cho ít nhất một người tham gia

Phân tích trên cho phép nhà thiết kế giao thức chọn quy mô của giải thưởng để nhắm mục tiêu vào một lượng tham gia nhất định theo trạng thái cân bằng đối xứng được tạo ra bởi mối quan hệ giữa x x và p p . Với hình phạt tham gia thấp, hàm chi phí của giao thức, mà chúng tôi biểu thị bằng C_p C p , là

C_p = c \cdot \Pr[\text{không tham gia}] + x \cdot \Pr[\text{tham gia}].
C p = c ⋅ Pr [ không tham gia ] + x ⋅ Pr [ tham gia ] .

Chi phí này là thứ mà giao thức tìm cách giảm thiểu, và giao thức phải đối mặt với sự đánh đổi khi chọn x x khi cho c c . Giá trị x x quá thấp sẽ khiến giao thức phải chịu hình phạt c c với xác suất cao; giá trị x x cao hơn sẽ trực tiếp tốn kém vì giao thức phải trả giải thưởng lớn hơn. Sử dụng thực tế là trong trạng thái cân bằng đối xứng, mỗi người chơi tham gia với xác suất p p , chúng ta có thể viết,

C_p = c \cdot (1-p)^n + x \cdot (1-(1-p)^n).
C p = c ⋅ ( 1 − p ) n + x ⋅ ( 1 − ( 1 − p ) n ) .

Với x = \frac{np}{1-(1-p)^n} x = n p 1 − ( 1 − p ) n (mối quan hệ chúng ta đã rút ra ở trên), điều này được đơn giản hóa thành

C_p = c \cdot (1-p)^n + np.
C p = c ⋅ ( 1 − p ) n + n p .

Đây là chi phí giao thức mà nó tìm cách giảm thiểu trên p \in [0,1] p ∈ [ 0 , 1 ] . Với xác suất tối ưu p^* p ∗ , giao thức có thể trực tiếp tính toán kích thước giải thưởng cần thiết để tạo ra trạng thái cân bằng đối xứng tại p^* p ∗ . Chúng tôi giảm thiểu chi phí của giao thức bằng cách sử dụng điều kiện bậc nhất,

\begin{align}\frac{\partial C_p}{\partial p} &= -cn(1-p)^{n-1} + n =0 \\&\ngụ ý p^* = 1-c^{-\frac{1}{n-1}}\end{align}
[Lỗi xử lý toán học]

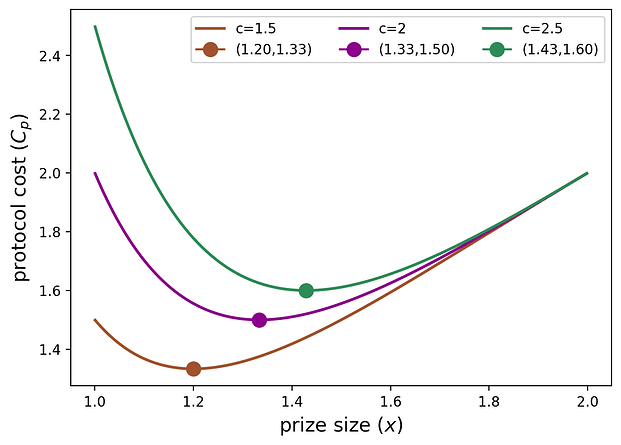
Đạo hàm bậc hai luôn âm trên p \in [0,1] p ∈ [ 0 , 1 ] , do đó p^* p ∗ thực sự là một bộ tối thiểu cục bộ duy nhất của chi phí giao thức. Biểu đồ sau đây cho thấy chi phí giao thức như một hàm của x x (có song ánh với p\in(0,1) p ∈ ( 0 , 1 ) ) với n=2 n = 2 và c=1.5,2,2.5 c = 1.5 , 2 , 2.5 , tương ứng.

tải lên_68cf7e34e09faa5dfee6d7ce96b8e0fb
tải lên_68cf7e34e09faa5dfee6d7ce96b8e0fb 1246×895 62,3 KB

Các giá trị x^* x ∗ (được biểu thị bằng các dấu chấm trong biểu đồ) đang tăng lên trong c c vì khi giao thức phải đối mặt với hình phạt cao hơn vì không tham gia, nó chọn x^* x ∗ cao hơn (dẫn đến p^* p ∗ cao hơn) để rất tự tin rằng ít nhất một người chơi sẽ tham gia. Từ p^* p ∗ , chúng tôi tính toán kích thước giải thưởng tối ưu ở dạng đóng là

\begin{align}x^* &= \frac{np^*}{1-(1-p^*)^n} \\&= \frac{n(1-c^{-1/(n-1)})}{1-c^{-n/(n-1)}}\end{align}
[Lỗi xử lý toán học]

Chúng tôi cũng tính toán chi phí giao thức tối ưu của

\begin{align}C_p^* &= c \cdot (1-p^*)^n + np^* \\&= n-(n-1) c^{-1/(n-1)}\end{align}
[Lỗi xử lý toán học]

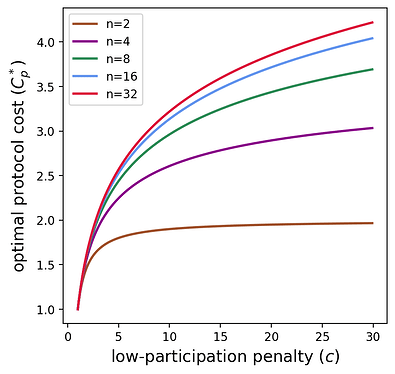
Biểu đồ bên dưới giúp hình dung chi phí này như một hàm của n,c n , c .

tải lên_32974a3ccb2b0fc03b6c63af46b5baa4
upload_32974a3ccb2b0fc03b6c63af46b5baa4 945×895 66,1 KB

Chúng ta thấy rằng khi hình phạt tham gia thấp tăng lên, chi phí giao thức dường như tăng theo logarit. Phần tiếp theo chính thức hóa mối quan hệ này bằng cách xem xét hành vi tiệm cận của chi phí giao thức.

3.2 Tiệm cận

Một câu hỏi tự nhiên nảy sinh về cách các giá trị của p^*, x^*, C_p^* p ∗ , x ∗ , C ∗ p thay đổi như một hàm của c c . Đặc biệt, một nhà thiết kế giao thức có thể muốn biết cách tiện ích của họ thay đổi như một hàm của c c giả sử có một số lượng lớn người chơi trong trò chơi, n n . Mở rộng (xem chú thích 4 để biết cách suy ra), chúng ta có

\begin{align}p^* &= \frac{\ln c}{n-1} + O\left(\frac{(\ln c)^2}{n^2}\right).\end{align}
[Lỗi xử lý toán học]

Tương tự như vậy, chúng ta có thể kiểm tra hành vi tiệm cận của x^* x ∗ (xem chú thích 5 để biết cách suy ra), đây là giải thưởng tối ưu cho giao thức giảm thiểu chi phí:

\begin{align}x^* = \frac{\ln c}{1 - 1/c} + O\left(\frac{(\ln c)^2}{n}\right).\end{align}
[Lỗi xử lý toán học]

Cuối cùng, chúng tôi kiểm tra hành vi tiệm cận của chi phí tối ưu được giao thức trả, C_p^* C ∗ p (xem chú thích 6 để biết cách suy ra):

\begin{align}C_p^* &=1 + \ln c + O\left(\frac{(\ln c)^2}{n}\right).\end{align}
[Lỗi xử lý toán học]

Quan trọng là chúng ta thấy rằng khi n\to\infty n → ∞ , tổng chi phí của giao thức được chia tỷ lệ thành 1+ \ln c 1 + ln c . Điều này rất tuyệt vời cho giao thức vì nó cung cấp một giới hạn logarit về chi phí như một hàm của tùy chọn bên ngoài. Hơn nữa, chi phí tối ưu không phụ thuộc vào n n . Điều này rất tiện lợi trong một thiết lập không cần xin phép vì giao thức có thể đặt giải thưởng tối ưu chỉ dựa trên chất lượng của tùy chọn bên ngoài (tức là hình phạt tham gia thấp) mà không cần biết có bao nhiêu người chơi! Điều này cũng có nghĩa là giao thức có thể chắc chắn rằng chi phí của họ bị giới hạn ngay cả khi số lượng người chơi trong trò chơi rất lớn. 7

Phần tiếp theo trả lời câu hỏi "chúng ta có thể vượt qua giới hạn logarit này không?" Chính thức hơn, liệu có tồn tại quy tắc thanh toán ẩn danh sao cho cân bằng đối xứng kết quả có chi phí giao thức C_p < 1+\ln c C p < 1 + ln không c ? Chúng tôi sẽ chỉ ra trong phần sau rằng câu trả lời là không! Chi phí giao thức bị giới hạn chặt chẽ bởi 1+\ln c 1 + ln c .

3.3 1+\ln c 1 + ln c ràng buộc là chặt chẽ

Note for the math/formalism-averse crowd: this section can be safely skipped!

Chúng ta biết rằng mỗi người chơi tham gia với xác suất p p trong trạng thái cân bằng đối xứng. Chúng ta cần chính thức hóa tính chất ẩn danh mà chúng ta đã phác thảo trong Phần 1.2 để so sánh cơ chế của chúng ta với các quy tắc thanh toán ẩn danh khác. Quy tắc thanh toán \pi(S,r) π ( S , r ) lấy đầu vào là tập hợp S\subseteq [n] S ⊆ [ n ] gồm những người tham gia đã tham gia và một hạt giống ngẫu nhiên r r , và đưa ra khoản thanh toán cho mỗi người tham gia. Cơ chế trong phần trước trả cho một người tham gia ngẫu nhiên giải thưởng xổ số x x với xác suất 1/|S | 1 / | S | nếu S S không rỗng và không trả cho ai nếu không. Chúng ta nói rằng cơ chế \pi(S,r) π ( S , r ) là ẩn danh (sau) nếu nó đối xứng từng điểm đối với các hành động của tác nhân. Về mặt hình thức, \pi π là ẩn danh sau sự kiện nếu với mọi r r và S S và mọi hoán vị \sigma σ , \pi(S,r)=\pi(\sigma(S),r) π ( S , r ) = π ( σ ( S ) , r ) . Khi một cơ chế ẩn danh, chúng ta có thể viết lại quy tắc thanh toán của nó thành \pi(S,r)=\pi(k,r) π ( S , r ) = π ( k , r ) trong đó k=|S| k =

Khu vực:
DeFi
AMM
Khai Thác Lợi Suất
Nguồn
Tuyên bố từ chối trách nhiệm: Nội dung trên chỉ là ý kiến của tác giả, không đại diện cho bất kỳ lập trường nào của Followin, không nhằm mục đích và sẽ không được hiểu hay hiểu là lời khuyên đầu tư từ Followin.
Thích
Thêm vào Yêu thích
Bình luận
Nội dung liên quan