Đồng tác giả @164zheng & @keccak255 ( Titania Research ). Cảm ơn @barnabe , @Julian , @banr1 và Alphaist vì những bình luận và thảo luận có giá trị của họ. Nghiên cứu này được hỗ trợ bởi khoản tài trợ Ethereum Foundation ESP (FY24-1744).
Tóm lại
Nếu nhà xây dựng hàng đầu trong một cuộc đấu giá khe cắm có thể cam kết đáng tin cậy là sẽ bỏ qua bất kỳ cuộc đấu giá khối nào, họ có thể khuyến khích người đề xuất chọn cuộc đấu giá khe cắm. Chiến lược này có thể tăng lợi nhuận của nhà xây dựng bằng cách giảm sự cạnh tranh và giảm giá thầu bắt buộc. Do đó, các cuộc đấu giá khe cắm có thể đáp ứng Lợi thế không đáng tin cậy thường xuyên hơn dự kiến. Cam kết như vậy định hình lại các động cơ và thay đổi lựa chọn tối ưu của người đề xuất.
Giới thiệu
Là một phần của cuộc thảo luận ePBS , định dạng của cuộc đấu giá mà theo đó những người xây dựng khối có được quyền xây dựng các khối thực thi đang được tranh luận. Có hai cuộc đấu giá trong giao thức chính thống: đấu giá khối và đấu giá khe.
Đấu giá khối là một cuộc đấu giá mà người đề xuất cam kết thực hiện một tải trọng vào cuối cuộc đấu giá. Ví dụ, MEV-boost là kiểu đấu giá này. Trong một cuộc đấu giá khối, người xây dựng phải cam kết tải trọng khối cụ thể khi gửi giá thầu.
Ngược lại, đấu giá khe là một cuộc đấu giá mà người đề xuất không cam kết với một tải trọng cụ thể mà thay vào đó là với một nhà xây dựng cụ thể vào cuối cuộc đấu giá. Trong trường hợp này, nhà xây dựng không cần phải gửi tải trọng thực hiện tại thời điểm đấu giá. Nhà xây dựng chiến thắng sẽ gửi tải trọng thực hiện sau đó. So với đấu giá khối, đấu giá khe có lợi thế là làm mịn doanh thu vì các nhà xây dựng trả giá theo giá trị kỳ vọng và các mức tăng đột biến MEV cực đại được tính trung bình theo thời gian.
Mặt khác, đấu giá khe cắm đã bị chỉ trích vì thiếu thuộc tính Không có lợi thế đáng tin cậy . Không có lợi thế đáng tin cậy có nghĩa là người đề xuất không có động lực để bán quyền xây dựng khối ngoài giao thức. Họ chỉ ra rằng đấu giá khối dự kiến sẽ mang lại lợi nhuận cao hơn cho người đề xuất so với đấu giá khe cắm. ( Khi nào nên bán khối của bạn ) Do đó, ngay cả khi người đề xuất có thể cam kết trong giao thức cho các khe cắm, họ vẫn có thể chọn tổ chức đấu giá khối ngoài giao thức để bán quyền xây dựng khối.
Bài nghiên cứu này xem xét lại các điều kiện mà đấu giá khe đáp ứng Không có lợi thế đáng tin cậy. Cụ thể, chúng tôi chỉ ra rằng khi người xây dựng có khả năng tạo ra khối có giá trị kỳ vọng cao nhất trong đấu giá khe có thể cam kết không tham gia đấu giá khối, họ có động lực để thực hiện cam kết như vậy, dẫn đến người đề xuất chọn đấu giá khe.
Lưu ý rằng bài đăng này vẫn ở mức thiết kế cơ chế trừu tượng; chúng tôi bỏ qua các chi tiết kỹ thuật phía máy khách. Điều quan trọng đối với mô hình là thông tin mà mỗi nhà xây dựng có khi đấu thầu. Trong một cuộc đấu giá khối, một nhà xây dựng đã mô phỏng một tải trọng bê tông và biết giá trị chính xác mà nó có thể nhận ra. Ngược lại, trong một cuộc đấu giá khe, nhà xây dựng chỉ nhìn thấy một kỳ vọng thống kê sơ bộ. (Trong thực tế, những người xây dựng đấu giá khe có thể quan sát các tín hiệu yếu, nhưng không đủ để xác định chính xác giá trị. Để rõ ràng hơn, chúng tôi mô hình hóa trường hợp khe như thể họ chỉ biết giá trị trung bình trước đó của họ.)
Người mẫu
Chúng tôi phân tích sự lựa chọn của người đề xuất giữa đấu giá khối và đấu giá khe bằng cách sử dụng khuôn khổ của trò chơi dạng mở rộng trong lý thuyết trò chơi. Đầu tiên, chúng tôi mô hình hóa hành vi và lợi nhuận của người đề xuất và người xây dựng. Sau đó, chúng tôi phân tích hai trường hợp—không có cam kết và có cam kết—và xác định thời điểm cam kết của người xây dựng có lợi nhuận.
Chúng ta hãy xem xét trò chơi dạng mở rộng sau:
Người chơi :
Một người đề xuất và n n người xây dựng i \in \{1, ..., n\} \equiv N i ∈ { 1 , . . . , n } ≡ N .
Người đề xuất bán quyền xây dựng một khối nhà tại vị trí k k thông qua một cuộc đấu giá giữa n n nhà xây dựng b_i b i .
Sở thích và giá trị
Tất cả người chơi đều trung lập về rủi ro với tiện ích gần như tuyến tính. Giá trị của khối mà người xây dựng i i có thể xây dựng trong một cuộc đấu giá khối là v_i^b v b i , được rút ra từ một hàm phân phối F_i^b F b i . Trong một cuộc đấu giá khe, giá trị khối của họ là v_i^s v s i , được rút ra từ một phân phối F_i^s F s i . Chúng độc lập với nhau và độc lập giữa các người xây dựng.
Giả sử người xây dựng 1 có giá trị khe mong đợi cao nhất và người xây dựng i i có giá trị khe mong đợi cao thứ i , E[v_1^s] \geq ... \geq E[v_n^s] E [ v s 1 ] ≥ . . . ≥ E [ v s n ] . ( E[\cdot] E [ ⋅ ] biểu thị giá trị mong đợi.)
Dòng thời gian
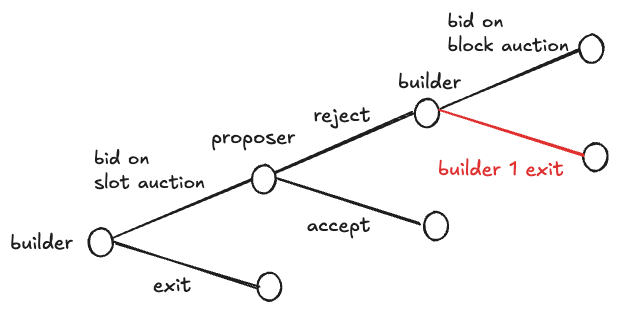
Trò chơi dạng mở rộng diễn ra như sau:
Giai đoạn 0: Cam kết
Nhà thầu 1 có thể cam kết không tham gia đấu giá theo khối.
Giai đoạn 1 – đấu giá slot
Đầu tiên, một cuộc đấu giá khe cắm theo kiểu Anh (giá thầu tăng dần) được tổ chức. Mỗi nhà xây dựng chỉ biết giá trị khối dự kiến của họ là E[v_i^s] E [ v s i ] ở giai đoạn này.
Cơ học
- Phiên đấu giá mở vào thời điểm 0 với giá cố định là 0.
- Cho đến thời hạn đã thông báo T_s T s , bất kỳ nhà thầu nào cũng có thể đưa ra giá thầu mới với bất kỳ quy mô nào, miễn là giá thầu đó phải vượt quá giá thầu hiện tại.
- Người xây dựng có thể tránh bằng cách không bao giờ nộp giá thầu (hoặc ngừng đấu thầu khi giá quá cao).
- Khi thời hạn T_s T s đến, việc đấu giá sẽ dừng lại ngay lập tức.
- Giá thầu cao nhất tại thời điểm đó—ký hiệu là $p_s$—sẽ thắng và chủ sở hữu của nó là w w trở thành người chiến thắng tạm thời .
- Chưa thu được khoản thanh toán nào và chưa có hàng hóa nào được chuyển giao.
Mỗi người xây dựng có thể chọn trả giá x_i^s x s i hoặc thoát khỏi cuộc đấu giá.
Giai đoạn 2 – lựa chọn của người đề xuất
Sau khi quan sát giá cuối cùng của khe cắm p_s p s , người đề xuất chọn:
Chấp nhận Đấu giá khe cắm: Người chiến thắng trả p_s p s cho người đề xuất và giành được quyền xây dựng một khối khe cắm. Phần thưởng của người xây dựng là v_i^s - p_s v s i − p s nếu họ thắng; nếu không thì là 0.
Từ chối Đấu giá khe và mở Đấu giá khối: Kết quả khe không có giá trị và trò chơi chuyển sang đấu giá khối.
Giai đoạn 3 – đấu giá theo khối (chỉ thực hiện nếu người đề xuất từ chối kết quả của vòng đấu giá)
Nếu người đề xuất mở một phiên đấu giá khối theo kiểu Anh, thì mỗi nhà xây dựng sẽ biết được giá trị khối chính xác của mình là v_i^b v b i , sau đó họ sẽ tham gia vào phiên đấu giá khối.
Người chiến thắng trong cuộc đấu giá khối sẽ trả p_b p b cho người đề xuất và nhận được giá trị của khối mà họ đã gửi. Phần thưởng của người xây dựng là v_i^b - p_b v b i − p b .
Kết quả
Chúng tôi phân tích trạng thái cân bằng của trò chơi này bằng phương pháp quy nạp ngược.
Giai đoạn 3 – đấu giá khối
Trong các cuộc đấu giá kiểu Anh, mỗi nhà thầu trả giá cho đến điểm mà phần thưởng của họ bằng không ở trạng thái cân bằng. Giả sử tập hợp những người tham gia đấu giá là M_b \subseteq N. M b ⊆ N .
Trong các cuộc đấu giá khối, mỗi nhà xây dựng biết giá trị khối thực tế của mình và trả giá lên đến giá trị đó. Người chiến thắng — nhà xây dựng y y có giá trị khối cao nhất — sẽ thắng cuộc đấu giá với giá trị cao thứ hai trong số những người tham gia:
E[p_b] = R_{b}(M_b) = E[\text{giây}(v_j^b)_{j\in M_b}] E [ p b ] = R b ( M b ) = E [ giây ( v b j ) j ∈ M b ] .
Người xây dựng quyết định có tham gia đấu giá hay không. Trong các cuộc đấu giá theo khối, mọi người xây dựng đủ điều kiện đều đạt được thặng dư dự kiến dương khi đấu giá, do đó tất cả người xây dựng đủ điều kiện đều tham gia.
Nếu người xây dựng 1 đã cam kết, cô ấy không đủ điều kiện. Do đó, phần thưởng cho người đề xuất là
R_{b}(N) R b ( N ) không có cam kết và R_b(N \setminus \{1\}) R b ( N ∖ { 1 } ) có cam kết.
Phần thưởng cho mỗi người xây dựng i i là E\!\bigl[\max(v_i^{b}-\text{second}(v_j^b)_{j\in M_b}, 0)\bigr] E [ tối đa ( v b i − giây ( v b j ) j ∈ M b , 0 ) ] .
Giai đoạn 2 - lựa chọn của người đề xuất
Giả sử p_s p s là giá thầu slot chiến thắng được ghi lại trong Giai đoạn 1. Người đề xuất chấp nhận kết quả slot nếu và chỉ nếu p_s \geq R_b p s ≥ R b . Nếu không, cô ấy từ chối và chạy phiên đấu giá khối.
Giai đoạn 1 – đấu giá slot
Không có bất kỳ cam kết nào
Lưu ý rằng người đề xuất sẽ từ chối bất kỳ kết quả nào tạo ra doanh thu thấp hơn giá trị dự kiến của phiên đấu giá khối R_b(N) R b ( N ) trong giai đoạn 2; do đó R_b(N) R b ( N ) đóng vai trò là giá dự trữ ngầm định.
Mỗi nhà xây dựng i i so sánh giá hiện tại với giá trị khe mong đợi của riêng mình E[v_i^s] E [ v s i ]
Nếu giá đấu giá đạt R_b(N) R b ( N ) , người đề xuất sẽ chấp nhận kết quả đấu giá khe. Sau đó, mỗi nhà xây dựng có động cơ tăng giá lên giá khe mong đợi của riêng mình E[v_i^s] E [ v s i ] , vì nếu không, cô ấy sẽ thua cuộc đấu giá và phần thưởng của cô ấy sẽ bằng không. Do đó, nhà xây dựng 1 thắng cuộc đấu giá với mức giá E[v_2^s] E [ v s 2 ] . Trong trường hợp này, phần thưởng của nhà xây dựng 1 là E[v_1^s] - E[v_2^s] E [ v s 1 ] − E [ v s 2 ] .
Vì vậy, không có nhà xây dựng nào ngoại trừ nhà xây dựng 1 có động cơ để đưa ra giá thầu cao hơn R_b(N) R b ( N ) khi phiên đấu giá mở vì điều đó khiến khoản thanh toán của họ bằng 0 và họ có thể kiếm được lợi nhuận dương trong phiên đấu giá khối. Chỉ có nhà xây dựng 1 có động cơ để đưa ra giá thầu cao hơn R_b(N) R b ( N ) nếu và chỉ nếu khoản thanh toán của cô ấy trong phiên đấu giá khe cắm vượt quá khoản thanh toán của phiên đấu giá khối:
E[v_1^s] - \max(E[v_2^s], R_b(N)) \geq E\!\bigl[\max(v_1^{b}-\text{giây}(v_j^b)_{j\in N}, 0)\bigr] E [ v s 1 ] − max ( E [ v s 2 ] , R b ( N ) ) ≥ E [ tối đa ( v b 1 − giây ( v b j ) j ∈ N , 0 ) ]
nếu đúng, phần thưởng của người xây dựng 1 là E[v_1^s] - \max(E[v_2^s], R_b(N)) E [ v s 1 ] − max ( E [ v s 2 ] , R b ( N ) ) .
Với cam kết của nhà xây dựng 1
Trong trường hợp này, giá dự trữ ngầm định trở thành R_b(N \setminus \{1\}) R b ( N ∖ { 1 } ) vì người xây dựng 1 cam kết không tham gia vào cuộc đấu giá khối. Do đó, khoản thanh toán của người xây dựng 1 trở thành
E[v_1^s] - \max(E[v_2^s], R_b(N \setminus \{1\})) E [ v s 1 ] − max ( E [ v s 2 ] , R b ( N ∖ { 1 } ) )
Giai đoạn 0 - cam kết của nhà xây dựng 1
Cam kết này là hợp lý đối với người xây dựng 1 nếu và chỉ nếu khoản tiền dự kiến của cô ấy trong phiên đấu giá khe cắm có cam kết vượt quá khoản tiền dự kiến của cô ấy trong phiên đấu giá khối mà không có cam kết:
E[v_1^s]- \max\bigl\{E[v_2^s],\;R_{\text{b}}(N\setminus\{1\})\bigr\} \geq E\bigl[\max(v_1^{b}-\text{giây}\{v_j^{b}\}_{j\in N}, 0)\bigr]. E [ v s 1 ] − max { E [ v s 2 ] , R b ( N ∖ { 1 } ) } ≥ E [ max ( v b 1 − giây { v b j } j ∈ N , 0 ) ] .
Nhìn chung, định nghĩa
Nếu U_{\text{slot không có commit}} \;\le\; U_{\text{block}} \;\le\; U_{\text{slot có commit}}, U slot không có commit ≤ Khối U ≤ U khe cắm với cam kết ,
Lời cam kết của người xây dựng 1 sẽ chuyển lựa chọn của người đề xuất từ đấu giá theo khối (không có cam kết) sang đấu giá theo vị trí (có cam kết).
nếu U_{\text{slot không có commit}} \;\ge\; U_{\text{block}} U slot không có commit ≥ Khối U ,
người đề xuất sẽ chọn đấu giá vị trí dù sao đi nữa; tuy nhiên, Nhà xây dựng 1 vẫn được hưởng lợi từ cam kết vì nó làm giảm dự trữ từ R_b(N) R b ( N ) xuống R_b(N \setminus \{1\}) R b ( N ∖ { 1 } ) và tăng thặng dư của cô ấy bằng hiệu số R_b(N) - R_b(N \setminus \{1\}) R b ( N ) − R b ( N ∖ { 1 } ) bất cứ khi nào R_b(N \setminus \{1\} ) \geq E[v_2^s] R b ( N ∖ { 1 } ) ≥ E [ v s 2 ] .
Cuộc thảo luận
Kết quả của chúng tôi cho thấy rằng cam kết đáng tin cậy của nhà xây dựng có thể chuyển người đề xuất từ đấu giá khối sang đấu giá khe. Nếu nhà xây dựng có giá trị khe dự kiến cao nhất hứa sẽ bỏ qua đấu giá khối và đưa ra giá thầu khe đủ lớn, người đề xuất sẽ kiếm được nhiều hơn từ đấu giá khe, trong khi nhà xây dựng phải đối mặt với ít sự cạnh tranh hơn và giữ được lợi nhuận lớn hơn.
Lưu ý rằng nếu không có cam kết nào được thực hiện và E[v_i^b] = E[v_i^s] E [ v b i ] = E [ v s i ] , thì doanh thu dự kiến của nhà xây dựng trong phiên đấu giá khối sẽ cao hơn so với phiên đấu giá theo vị trí.
Bằng chứng
Khi người xây dựng 1 cam kết, phiên đấu giá khe cắm có thể—mặc dù chỉ trong một số trường hợp hạn hẹp—mang lại tổng doanh thu cao hơn. Hơn nữa, nếu khoản thanh toán dự kiến của người xây dựng 1 trong phiên đấu giá khe cắm vượt quá khoản thanh toán dự kiến của cô ấy trong phiên đấu giá khối, thì khả năng người đề xuất sẽ lựa chọn phiên đấu giá khe cắm sẽ tăng cao hơn nữa. Ngoài ra, định dạng khe cắm trở nên hấp dẫn hơn nữa—và do đó có nhiều khả năng được lựa chọn hơn—khi người xây dựng có doanh thu khe cắm cao nhất trải qua sự gia tăng lớn hơn so với thu nhập từ phiên đấu giá khối của cô ấy so với bất kỳ người xây dựng nào khác.
Hơn nữa, khi các nhà xây dựng hợp nhất và lĩnh vực này trở nên tập trung hơn, giá trị khối cao thứ hai dự kiến—giá dự phòng hoặc giá “dự trữ” của người đề xuất—sẽ giảm. Giá dự trữ thấp hơn khiến cam kết của nhà xây dựng 1 dễ xóa hơn, do đó cam kết trở nên mạnh mẽ hơn và phiên đấu giá khe cắm có nhiều khả năng được chọn hơn.
Phần khó là làm cho cam kết của người xây dựng trở nên đáng tin cậy. Trong thực tế, điều này có thể cần một trái phiếu lớn trên chuỗi (ví dụ, thông qua EigenLayer AVS) hoặc một chứng thực phần cứng tốn kém để phá vỡ. Ai cam kết trước cũng quan trọng: nếu người đề xuất cam kết đấu giá khối trước, lời hứa của người xây dựng sẽ mất hiệu lực; nếu người xây dựng cam kết trước, người đề xuất sẽ bị đẩy về phía đấu giá khe.
Cũng sẽ rất thú vị khi điều tra xem kết luận nào sẽ nảy sinh nếu chúng ta giả định các giá trị phụ thuộc lẫn nhau và mô hình hóa cuộc cạnh tranh như một cuộc đấu giá tăng dần. Theo các giá trị phụ thuộc lẫn nhau, một cuộc đấu giá giá tăng dần sẽ tiết lộ các tín hiệu khi đồng hồ tích tắc, tăng giá dự phòng của người đề xuất trong khi tô bóng lời nguyền của người chiến thắng sâu hơn sẽ cắt giảm thặng dư của mỗi nhà xây dựng. Một cam kết "chỉ có khe" vẫn có thể khiến người đề xuất hướng tới cuộc đấu giá khe, nhưng chỉ khi lợi thế riêng của nhà xây dựng hàng đầu vượt qua rào cản cao hơn này—cửa sổ khả thi thu hẹp lại, nhưng không nhất thiết phải biến mất. Điều này vẫn là một phỏng đoán; một mô hình chính thức được hoãn lại cho công việc trong tương lai.
Cuối cùng, vì các cuộc đấu giá lặp lại sau mỗi 12 giây với hầu hết cùng một nhà xây dựng, bối cảnh thực sự là một trò chơi lặp lại. Nghiên cứu các động lực dài hạn đó—và thử nghiệm chúng với dữ liệu đấu thầu trong quá khứ—là một nhiệm vụ quan trọng cho nghiên cứu trong tương lai.