Sebastien Bubeck, cựu Phó Chủ tịch AI của Microsoft và Nhà khoa học Xuất sắc, đã viết một bài đăng bày tỏ sự kinh ngạc trước phát hiện GPT-5 Pro đã giải được một khoảng chưa giải được trong một bài toán từ đầu. Khám phá này đã được chia sẻ rộng rãi, và chủ tịch của OpenAI cho rằng AI có thể thúc đẩy nghiên cứu toán học.
Liệu AI có thực sự có thể giải quyết được những vấn đề tiên tiến của nhân loại không?
Ví dụ, các bài toán như giả thuyết Poincaré, giải phương trình Maxwell, Định lý cuối cùng của Fermat và giả thuyết Riemann.
Ngày nay câu hỏi này đã có câu trả lời.
AI thực sự có thể làm được điều đó! Nó hoàn toàn độc lập và không tham khảo bất kỳ phương pháp hiện có của con người.
Đêm qua, GPT-5 Pro đã có thể giải quyết hoàn toàn một bài toán phức tạp từ đầu.
Và một lần nữa, nó không sử dụng bất kỳ phương pháp chứng minh nào của con người trước đó.
Và câu trả lời của nó tốt hơn phương pháp trong bài báo.
May mắn thay cho nhân loại, các tác giả của bài báo sau đó đã cung cấp một phương pháp mới vượt trội hơn AI.
Sebastien Bubeck là kỹ sư nghiên cứu tại OpenAI và trước đây từng giữ chức Phó chủ tịch kiêm Nhà khoa học xuất sắc về Trí tuệ nhân tạo tại Microsoft.
Anh ta ném một tờ giấy trực tiếp vào GPT-5 Pro.
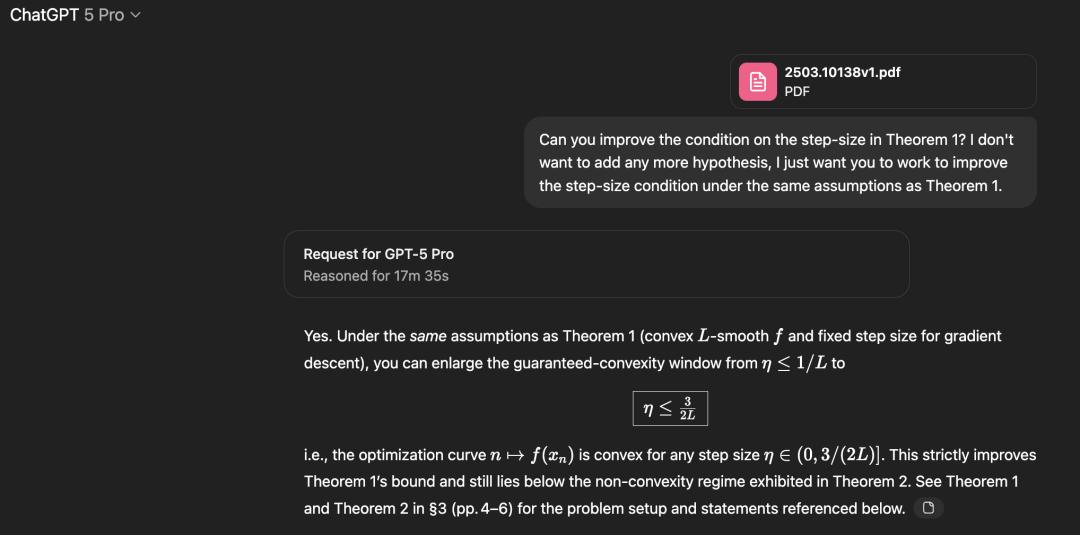
Bài báo này nghiên cứu một câu hỏi rất tự nhiên: trong tối ưu hóa lồi trơn, trong điều kiện nào thì bước kích thước η của phương pháp giảm độ dốc đáp ứng để đường cong được tạo bởi giá trị hàm tương ứng với điểm lặp là lồi?
Địa chỉ bài báo: https://arxiv.org/pdf/2503.10138v1
Trong phiên bản v1 của bài báo, họ đã chứng minh rằng tính chất này vẫn đúng nếu η nhỏ hơn 1/L (trong đó L là độ mịn).
Nếu η lớn hơn 1,75/L, tác giả đã xây dựng một phản ví dụ.
Do đó, câu hỏi chưa được giải quyết là: điều gì xảy ra trong khoảng [1/L,1,75/L].
Trước tiên, tôi xin giải thích ngắn gọn về vấn đề này.
Phương pháp giảm dần độ dốc (gradient giảm) giống như đi xuống dốc. Với mỗi bậc, bạn chọn một kích thước bậc, η . L có thể được coi là độ cong của địa hình (càng lớn thì càng dốc/nhạy cảm hơn).
Bài báo không chỉ quan tâm đến việc "liệu nó có đi xuống hay không" (giảm đơn điệu), mà còn xem liệu quỹ đạo đi xuống có "lồi" hay không: nghĩa là, tiến trình của mỗi bước sẽ không dao động và sẽ không "giống như một bệ đỡ ở phía trước và đột nhiên nhảy xuống vách đá ở phía sau".
Điều này rất hữu ích để biết khi nào nên dừng lại - hình dạng lồi có nghĩa là nó đang trở nên ổn định hơn và sẽ không đột ngột rơi xuống nữa.
Sebastien đã sử dụng GPT-5 Pro để giải quyết khoảng thời gian chưa được giải quyết này và mô hình đã đẩy giới hạn dưới đã biết từ 1/L lên 1,5/L.
Sau đây là bằng chứng được đưa ra bởi GPT-5 Pro.
Mặc dù thoạt nhìn có vẻ không ấn tượng, nhưng toàn bộ quá trình kiểm tra lại có vẻ rất tinh tế.
Khám phá này ban đầu khiến Sebastien phấn khích một thời gian, và ông thậm chí còn muốn xuất bản trực tiếp một bài báo trên arXiv.
Tuy nhiên, con người vẫn đi trước AI một bước.
Các tác giả ban đầu của bài báo đã nhanh chóng phát hành phiên bản v2, phiên bản này đã được hoàn thiện hoàn toàn. Họ đã thay đổi ngưỡng thành 1,75/L .
Sebastien cho rằng phát hiện này vẫn rất đáng khích lệ. Tại sao? Chẳng phải AI đã đánh bại con người sao?
Bởi vì trong bằng chứng, GPT-5 Pro đã cố gắng chứng minh 1.5/L thay vì 1.75/L, điều này cũng cho thấy GPT-5 Pro không trực tiếp tìm kiếm phiên bản v2.
Ngoài ra, bằng chứng trên cũng rất khác so với bằng chứng v2. Nó giống như một sự phát triển hơn của bằng chứng v1.
Theo góc nhìn này, năng lực AI ngày nay không chỉ dừng lại ở trình độ tiến sĩ mà thường còn vượt xa hơn thế.
Khám phá này cũng khiến nhiều chuyên gia cho rằng lĩnh vực tiếp theo mà AI có thể thay đổi và tác động là toán học.
Với sự trợ giúp của AI, ranh giới kiến thức của con người sẽ lại được mở rộng.
Greg Brockman, chủ tịch của OpenAI, thậm chí còn cho rằng đây có thể là dấu hiệu cho thấy sức sống của AI trong toán học.
Ngoài ra, khám phá lần khác với thông báo chính thức trước đây của OpenAI rằng công ty này đã giành được huy chương vàng IMO và IOI.
Mô hình được sử dụng để giải các bài toán lần là phiên bản hướng đến người dùng của GPT-5 Pro, không phải là mô hình suy luận nội bộ.
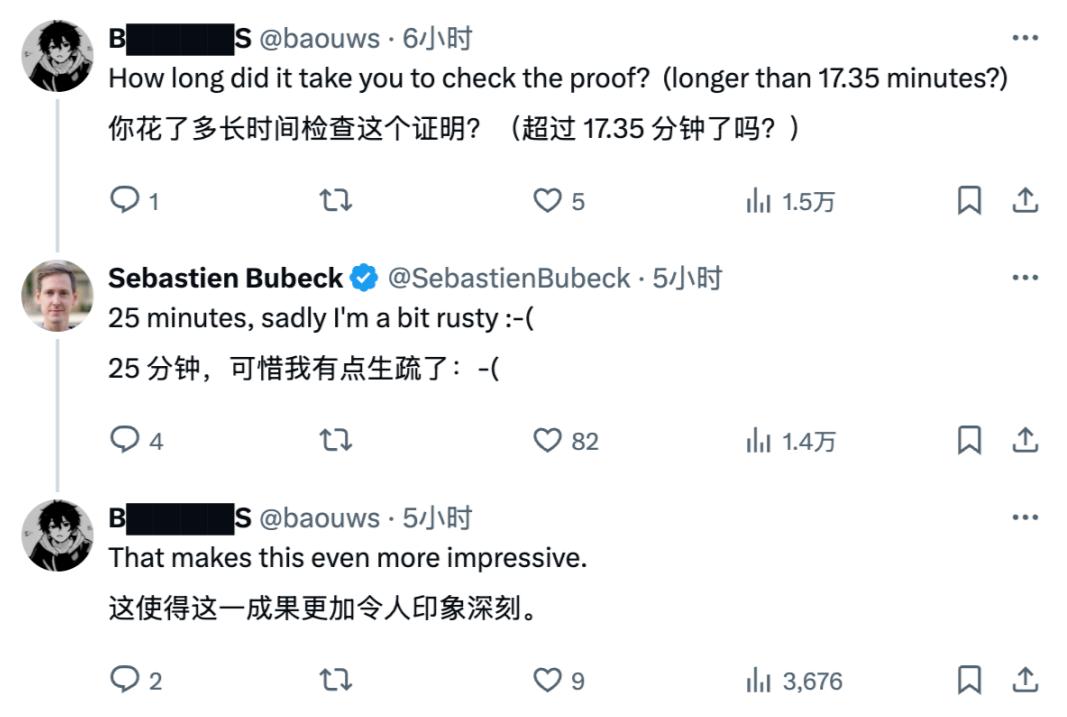
Sebastien cho biết kết luận này đã được chính ông xác minh trong vòng 25 phút.
Với tư cách là cựu phó chủ tịch trí tuệ nhân tạo và nhà khoa học lỗi lạc tại Microsoft, bằng chứng của ông hẳn là chính xác và có vẻ như AI thực sự đã chứng minh được bài toán toán học này.
GPT-5 đã nhận được nhiều đánh giá trái chiều kể từ khi phát hành.
Tuy nhiên, GPT-5 Pro thực sự đã đạt tới và thậm chí vượt xa cái mà Altman gọi là AI "cấp độ tiến sĩ".
Mặc dù vấn đề được giải quyết lần chưa vượt qua được con người, nhưng dấu hiệu về khả năng tự chủ và tự khám phá hoàn toàn này vẫn thể hiện được năng lực của AI.
Điều này làm tôi nhớ đến MOSS trong The Wandering Earth, cũng là một AI có khả năng tự khám phá, tự tổ chức và tự lập trình.
Sebastien là một người rất có năng lực.
Hiện anh đang làm việc về trí tuệ nhân tạo tại OpenAI.
Trước đó, Sebastien là Phó chủ tịch và Nhà khoa học trưởng tại Microsoft , nơi ông làm việc tại Microsoft Research trong 10 năm (ban đầu là trong nhóm nghiên cứu lý thuyết).
Sebastien cũng từng là trợ lý giáo sư tại Đại học Princeton trong 3 năm.
Sebastien đã dành 15 năm đầu sự nghiệp của mình để nghiên cứu về tối ưu hóa lồi , thuật toán trực tuyến và tính mạnh mẽ đối nghịch trong học máy.
Ông đã giành được lần giải thưởng bài báo hay nhất cho các công trình nghiên cứu này (bao gồm STOC2023, NeurIPS2018 và Giải thưởng Bài báo hay nhất năm 2021, Giải thưởng Bài báo hay nhất của sinh viên năm 2018 và 2023 được trao tặng khi hợp tác với các thực tập sinh của Microsoft Research, Giải thưởng Bài báo hay nhất COLT2016 và Giải thưởng Bài báo hay nhất của sinh viên năm 2009).
Hiện nay, ông tập trung hơn vào việc tìm hiểu cách trí thông minh xuất hiện trong các mô hình ngôn ngữ lớn và cách sử dụng sự hiểu biết này để cải thiện mức độ thông minh của các mô hình ngôn ngữ lớn, có lẽ cuối cùng đạt được trí tuệ nhân tạo tổng quát (AGI).
Sebastien gọi phương pháp này là "vật lý AGI" vì nó cố gắng tiết lộ cách các bộ phận của hệ thống AI hoạt động cùng nhau ở các quy mô khác nhau (tham số, nơ-ron, nhóm nơ-ron, lớp, chuỗi dữ liệu, v.v.) để tạo ra hành vi đáng ngạc nhiên và không mong đợi của các mô hình này.
Có vẻ như các nhà toán học và nhà khoa học như Sebastien đang nỗ lực hết sức để giải mã bí ẩn hộp đen của các mô hình lớn.
Tôi hy vọng rằng trong khi AI mở rộng ranh giới nhận thức của con người, con người cũng có thể khám phá ra bí mật của các mô hình lớn.
Tham khảo:
https://x.com/Sebastien%20Bubeck/status/1958198661139009862
Bài viết này được trích từ tài khoản công khai WeChat "Xinzhiyuan" , tác giả: Xinzhiyuan, biên tập: Dinghui và được 36Kr cấp phép xuất bản.