Tóm lại
Bằng chứng Phạm vi Đơn giản. Chỉ cần 6 ECMUL và 3 ECADD (37K gas) để xác minh Bằng chứng Phạm vi của đồng tiền riêng tư dựa trên Cam kết Pedersen trên Máy ảo Ethereum (EVM). Thiết lập và cam kết đầu tiên yêu cầu zkSNARK, nhưng sau đó, chi phí được giảm thiểu. Đối với mỗi giao dịch được tạo ở phía máy khách, nó cũng không yêu cầu tính toán ZKP.
Bài báo đầy đủ kèm theo bằng chứng bảo mật: https://eprint.iacr.org/2025/1811.pdf
Các bước:
G,H,B là các điểm độc lập trên một đường cong.
Thiết lập một lần cho mỗi người chứng minh (người gửi Token )
- Lấy mẫu a ← Zq và đặt neo công khai U = aB.
- Tạo một cây Merkle với các điểm trên đường cong. Với mỗi X ∈ {1, . . . , 2 n}, hãy xác định tải trọng lá aXG
- Với NIZK trên chuỗi, hãy chứng minh gốc Merkle của cây bao gồm aXG. (bằng chứng trước phạm vi)
Chứng minh (khi gửi Token)
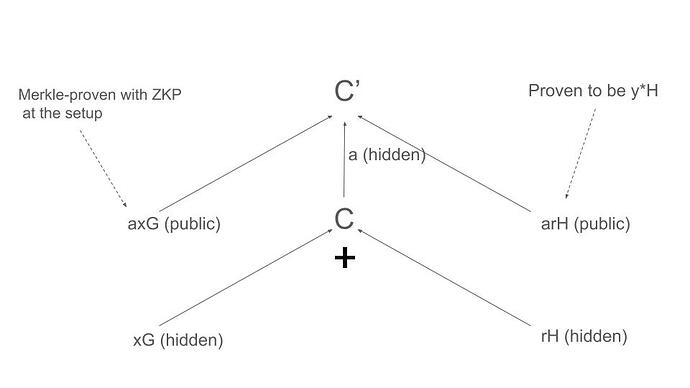
- Thực hiện cam kết Pedersen C = xG + rH với số lượng Token x và ẩn r. (x, r, xG và rH không được hiển thị)
- Nộp C, C' = aC, axG và bằng chứng Merkle của nó, bằng chứng Chaum-Pedersen DLEQ của (U, B) và (C', C), arH và bằng chứng của giao thức Schnorr của (arH, H)
Xác minh (rằng C nằm trong phạm vi x trên Máy ảo Ethereum (EVM))
1, Sử dụng Chaum-Pedersen DLEQ để kiểm tra xem (U, B) và (C', C) có cùng một rời rạc
2. Sử dụng giao thức Schnorr hoặc ECDSA để kiểm tra xem chất chứng minh có thể tạo ra arH từ H hay không.
3. Kiểm tra Merkle Proof của axG trong cây thiết lập.
4. Kiểm tra C' = axG + arH
## Tại sao Chaum-Pedersen DLEQ và U=aB là cần thiết
Nếu chúng ta sử dụng giao thức Schnorr hoặc ECDSA để kiểm tra mối quan hệ của (C', C), một trình chứng minh độc hại có thể tạo ra C' = yC và C = (bigX)G + rH trong đó y = ax/(bigX). yrH cũng sẽ được xác minh.
Làm thế nào để làm cho cây nhỏ hơn
Việc tạo một cây với tất cả các số nguyên có nonce sẽ Bit khó khăn. Việc tạo một cây điểm bằng cách sử dụng các số ngẫu nhiên giới hạn, nhân các lá với các số vô hướng và thêm một điểm vào chuỗi sẽ giúp ích rất nhiều, vì không ai có thể đoán được các số ngẫu nhiên từ các điểm trên đường cong của cây.